1.3.1: ¿Qué es lo mismo?

Lección

Vamos a decidir si las formas son iguales.

Ejercicio\(\PageIndex{1}\): Find the Right Hands

Las manos de una persona son imágenes especuladas unas de otras. En el diagrama, se etiqueta una mano izquierda. Sombra todas las manos correctas.

Figura\(\PageIndex{1}\)

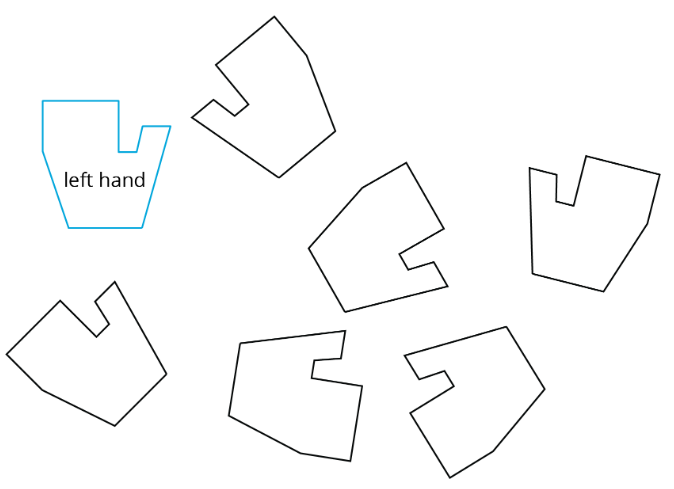
Ejercicio\(\PageIndex{2}\): Are They the Same?

Por cada par de formas, decide si son iguales o no.

Las formas de la Figura E no coinciden, la forma del rompecabezas de la derecha tiene una pestaña inferior derecha que la misma pestaña de la forma del rompecabezas izquierda.

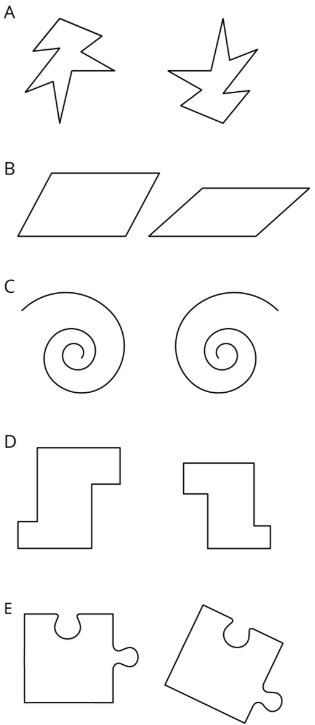
Ejercicio\(\PageIndex{3}\): Area, Perimeter, and Congruence

Figura\(\PageIndex{3}\)

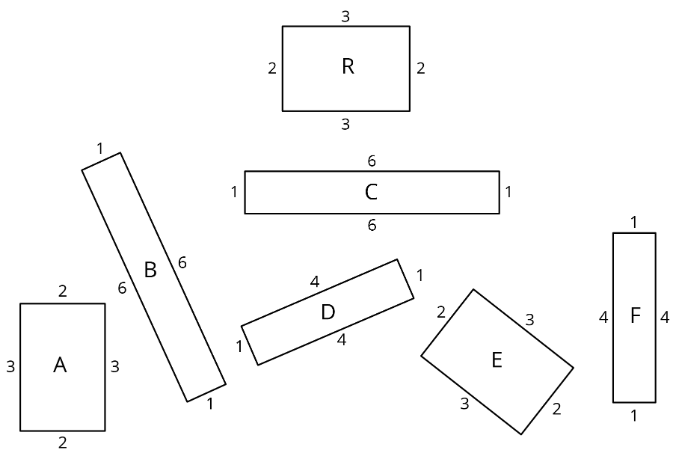
1. ¿Cuál de estos rectángulos tiene la misma área que Rectángulo R pero diferente perímetro?
2. ¿Qué rectángulos tienen el mismo perímetro pero diferente área?
3. ¿Cuáles tienen la misma área y el mismo perímetro?
4. Utilice materiales del kit de herramientas de geometría para decidir qué rectángulos son congruentes. Sombra rectángulos congruentes con el mismo color.

¿Estás listo para más?

En cuadrado\(ABCD\), puntos\(E\),\(F\),\(G\), y\(H\) son puntos medios de sus respectivos lados. ¿Qué fracción de cuadrado\(ABCD\) está sombreada? Explica tu razonamiento.

Figura\(\PageIndex{4}\)

Resumen

Congruente es un nuevo término para una idea que ya hemos estado usando. Decimos que dos figuras son congruentes si una puede alinearse exactamente con la otra por una secuencia de transformaciones rígidas. Por ejemplo, el triángulo\(EFD\) es congruente con el triángulo\(ABC\) porque se pueden emparejar reflejando el triángulo\(ABC\) a lo largo seguido de la traducción que muestra la flecha. Observe que todos los ángulos y longitudes laterales correspondientes son iguales.

Figura\(\PageIndex{5}\): Triángulo A B C, triángulo A B primo C, flecha discontinua de B primo al punto F y triángulo E F D. El triángulo A B primo C es la imagen del triángulo A B C después de la reflexión sobre A C. El ángulo A es 63 punto 4 grados, ángulo B es 71 punto 6 grados y ángulo C es 45 grados. El lado A B es 2 punto 2 4, el lado B C es 2 punto 8 3 y el lado A C es 3 punto 0 0. El ángulo E es 63 punto 4 grados, el ángulo F es 71 punto 6 grados y el ángulo D es 45 grados. El lado E F es 2 punto 2 4, el lado F D es 2 punto 8 3 y el lado D E es 3 punto 0 0.

Aquí hay algunos otros datos sobre cifras congruentes:

• No necesitamos verificar todas las medidas para demostrar que dos figuras son congruentes; solo tenemos que encontrar una secuencia de transformaciones rígidas que coincidan con las figuras.
• Una figura que parece una imagen especular de otra figura puede ser congruente con ella. Esto significa que debe haber una reflexión en la secuencia de transformaciones que coincida con las figuras.
• Dado que dos polígonos congruentes tienen la misma área y el mismo perímetro, una forma de mostrar que dos polígonos no son congruentes es mostrar que tienen un perímetro o área diferente.

Entradas en el glosario

Definición: Congruente

Una figura es congruente con otra si se puede mover con traslaciones, rotaciones y reflejos para encajar exactamente sobre la otra.

En la figura, el Triángulo A es congruente con los Triángulos B, C y D. Una traslación toma el Triángulo A al Triángulo B, una rotación toma el Triángulo B al Triángulo C y una reflexión lleva al Triángulo C al Triángulo D.

Figura\(\PageIndex{6}\)

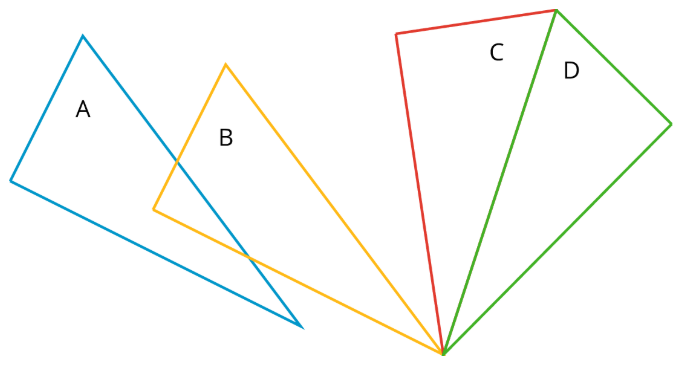
Practica

Ejercicio\(\PageIndex{4}\)

Si dos rectángulos tienen el mismo perímetro, ¿tienen que ser congruentes? Explica cómo sabes.

Ejercicio\(\PageIndex{5}\)

Dibuja dos rectángulos que tengan la misma área, pero que no sean congruentes.

Ejercicio\(\PageIndex{6}\)

Para cada par de formas, decida si las dos formas son congruentes o no. Explica tu razonamiento.

1.

Figura\(\PageIndex{7}\)

2.

Figura\(\PageIndex{8}\)

Ejercicio\(\PageIndex{7}\)

1. Refleja el cuadrilátero A sobre el\(x\) eje. Etiquetar la imagen cuadrilátero B. Refleja el cuadrilátero B sobre el\(y\) eje. Etiquetar la imagen C.

Figura\(\PageIndex{9}\)

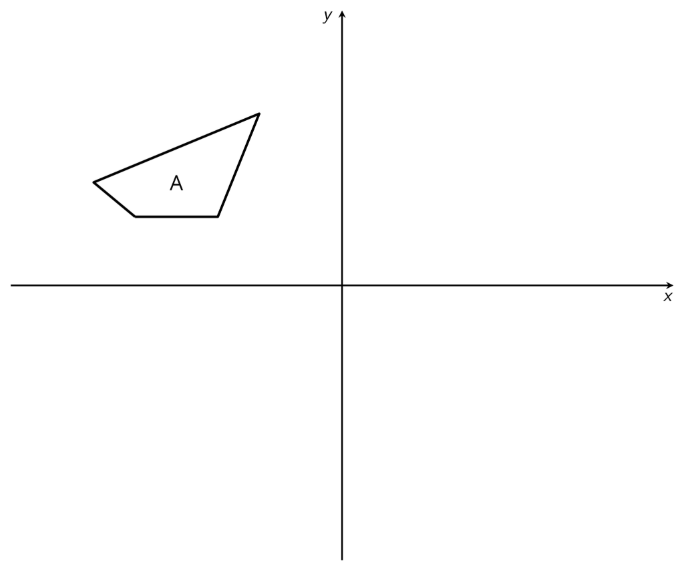
2. ¿Los cuadriláteros A y C son congruentes? Explica cómo sabes.

Ejercicio\(\PageIndex{8}\)

El punto\((-2,-3)\) se gira 90 grados en sentido antihorario usando el centro\((0,0)\). ¿Cuáles son las coordenadas de la imagen?
A:\((-3,-2)\)

B:\((-3,2)\)

C:\((3,-2)\)

D:\((3,2)\)

(De la Unidad 1.1.6)

Ejercicio\(\PageIndex{9}\)

Describir una transformación rígida que lleva el Polígono A al Polígono B.

Figura\(\PageIndex{10}\): Polígono A y su polígono de imagen B en un plano de coordenadas, origen\(O\). Escala del eje horizontal negativo 6 a 6 por 1's. Escala del eje vertical negativo 3 a 3 por 1's. El polígono A tiene coordenadas (negativo 6 coma 2), (negativo 6 coma 3), (negativo 2 coma 3), (negativo 2 coma 1), (negativo 3 coma 1) y (negativo 3 coma 2). El triángulo B tiene coordenadas (6 coma negativa 2), (6 coma negativa 3), (2 coma negativa 3), (2 coma negativa 1), (3 coma negativa 1) y (3 coma negativa 2).

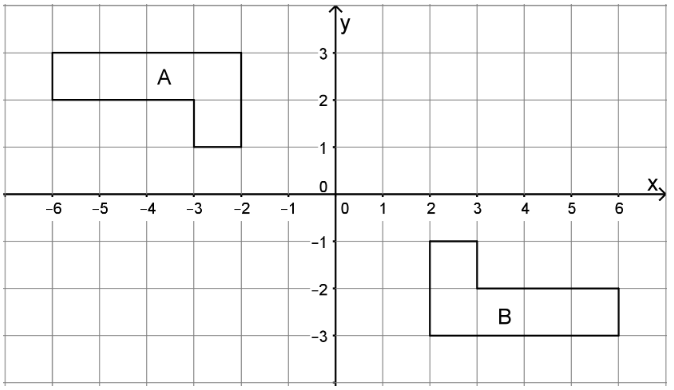
(De la Unidad 1.2.1)