1.3.2: Polígonos congruentes

Última actualización
Guardar como PDF

Page ID: 118659

Illustrative Mathematics
OpenUp Resources

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Lección

Decidamos si dos cifras son congruentes.

Ejercicio$\PageIndex{1}$: Translated Images

Todos estos triángulos son congruentes. A veces podemos llevar una figura a otra con una traducción. Sombra los triángulos que son imágenes de triángulo$ABC$ bajo una traslación.

Ejercicio$\PageIndex{2}$: Congruent Pairs (Part 1)

Para cada uno de los siguientes pares de formas, decida si son o no congruentes. Explica tu razonamiento.

La figura H G F E es la imagen de la figura A B C D después de una rotación de 180 grados, seguida de una traslación a la izquierda 3 y abajo de 2 unidades. A B C D tiene las coordenadas A (5 coma 0), B (4 coma 2), C (3 coma 1) y D (1 coma 1). H G F E tiene las coordenadas H (negativo 6 coma 0), G (negativo 5 coma negativo 2), F (negativo 4 coma negativo 1 y E (negativo 2 coma negativo 1).

Figura$\PageIndex{3}$: Dos pentágonos en un plano coordenado. Pentágono ABCDE no es convexo y tiene coordenadas A (negativo 4 coma 0), B (negativo 2 coma 1), C (negativo dos coma 4), D (negativo 3 coma 3) y E (negativo 4 coma 3). El Pentágono FGHIJ es convexo y tiene las coordenadas F (1 coma 2), G (3 coma 1), H (4 coma 2), I (4 coma 4) y J (2 coma 4).

Figura$\PageIndex{4}$: Dos triángulos D E F y A B C en un plano de coordenadas. Triángulo D E F es la imagen de los triángulos A B C después de la rotación de 90 grados, seguido de una traslación a la izquierda 3 y hacia abajo 2 unidades. El triángulo A B C tiene las coordenadas A (2 coma negativa 2), B (6 coma 0) y C (6 coma 2). El triángulo D E F tiene las coordenadas D (negativo 1 coma 0), E (negativo 3 coma 4) y F (negativo 5 coma 4).

Ejercicio$\PageIndex{3}$: Congruent Pairs (Part 2)

Por cada par de formas, decide si la Forma A es congruente o no con la Forma B. Explica cómo sabes.

La Figura B tiene los puntos P (6 coma 5), Q (8 coma 5), R (8 coma 2), S (9 coma 1), T (9 coma 0) y U (7 coma 0).

La Figura B tiene los puntos P (3 coma negativa 1), Q (3 coma 2), R (6 coma 2), S (6 coma 1), T (4 coma 1) y U (4 coma negativa 1).

La Figura B es un cuadrado con longitudes laterales 5 unidades y tiene puntos P (2 coma 1), Q (7 coma 1), R (7 coma 6) y S (2 coma 6).

La Figura B tiene los puntos P (3 coma negativa 1), Q (3 coma 2), R (6 coma 2) y S (6 coma 1).

La Figura B es un rombo con longitudes laterales cercanas a 2 puntos 8 unidades y tiene puntos P (3 coma 3), Q (5 coma 5), R (7 coma 3) y S (5 coma 1).

¿Estás listo para más?

Un polígono tiene 8 lados: cinco de longitud 1, dos de longitud 2 y uno de longitud 3. Todos los lados se encuentran en líneas de rejilla. (Puede ser útil usar papel cuadriculado cuando se trabaja en este problema).

Encuentra un polígono con estas propiedades.
¿Hay un segundo polígono, no congruente con el primero, con estas propiedades?

Ejercicio$\PageIndex{4}$: Building Quadrilaterals

Tu profesor te dará un conjunto de cuatro objetos.

Haz un cuadrilátero con tus cuatro objetos y registra lo que has hecho.
Compara tu cuadrilátero con el de tu pareja ¿Son congruentes? Explica cómo sabes.
Repita los pasos 1 y 2, formando diferentes cuadriláteros. Si tus primeros cuadriláteros no fueron congruentes, ¿puedes construir un par que sea? Si tus primeros cuadriláteros fueron congruentes, ¿puedes construir un par que no lo sea? Explique.

Resumen

¿Cómo sabemos si dos figuras son congruentes?

Si copiamos una figura en papel de calco y movemos el papel para que la copia cubra exactamente la otra figura, entonces eso sugiere que son congruentes.
Podemos demostrar que dos figuras son congruentes al describir una secuencia de traslaciones, rotaciones y reflexiones que mueven una figura sobre la otra para que coincidan exactamente.

¿Cómo sabemos que dos figuras no son congruentes?

Si no hay correspondencia entre las cifras donde las partes tienen igual medida, eso prueba que las dos cifras no son congruentes. En particular,
- Si dos polígonos tienen diferentes conjuntos de longitudes laterales, no pueden ser congruentes. Por ejemplo, la figura de la izquierda tiene longitudes laterales 3, 2, 1, 1, 2, 1. La figura de la derecha tiene longitudes laterales 3, 3, 1, 2, 2, 1. No hay manera de hacer una correspondencia entre ellos donde todos los lados correspondientes tengan la misma longitud.
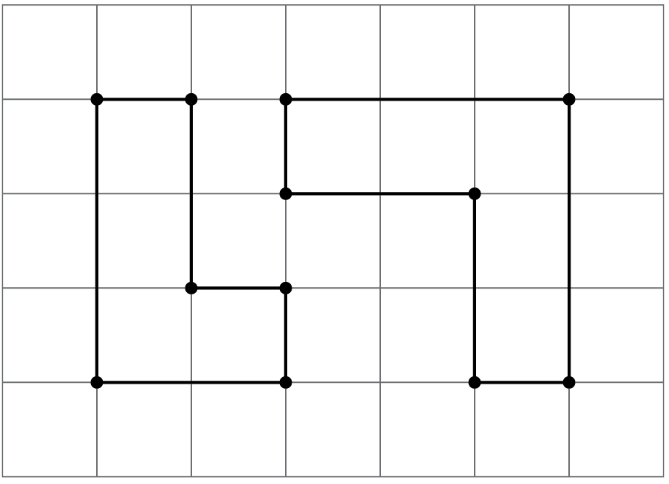
  $clipboard_e14a802623d3fa306d87c8cca1d0d2fab.png$
  Figura$\PageIndex{11}$
- Si dos polígonos tienen las mismas longitudes de lado, pero sus órdenes no pueden coincidir a medida que recorre cada polígono, los polígonos no pueden ser congruentes. Por ejemplo, el rectángulo no$ABCD$ puede ser congruente con el cuadrilátero$EFGH$. A pesar de que ambos tienen dos lados de longitud 3 y dos lados de longitud 5, no se corresponden en el mismo orden. En$ABCD$, el orden es 3, 5, 3, 5 o 5, 3, 5, 3; en$EFGH$, el orden es 3, 3, 5, 5 o 3, 5, 5, 3 o 5, 5, 3, 3.
  $clipboard_e5730be57aa6246a5ed1e24ef5910183a.png$
  Figura$\PageIndex{12}$: Dos figuras, A B C D y E F G H. La figura A B C D es un rectángulo con longitud lateral 3 y base y longitud superior 5. La Figura E F G H tiene una longitud base 5, la longitud superior es 3, la longitud del lado izquierdo es 3 y la longitud del lado derecho es 5.
- Si dos polígonos tienen las mismas longitudes de lado, en el mismo orden, pero diferentes ángulos correspondientes, los polígonos no pueden ser congruentes. Por ejemplo, el paralelogramo no$JKLM$ puede ser congruente con el rectángulo$ABCD$. A pesar de que tienen las mismas longitudes de lado en el mismo orden, los ángulos son diferentes. Todos los ángulos adentro$ABCD$ son ángulos rectos. En$JKLM$, los ángulos$J$ y$L$ son menores a 90 grados y ángulos$K$ y$M$ son más de 90 grados.
  $clipboard_ed7763497da06bb993f8042868d3fa857.png$
  Figura$\PageIndex{13}$

Entradas en el glosario

Definición: Congruente

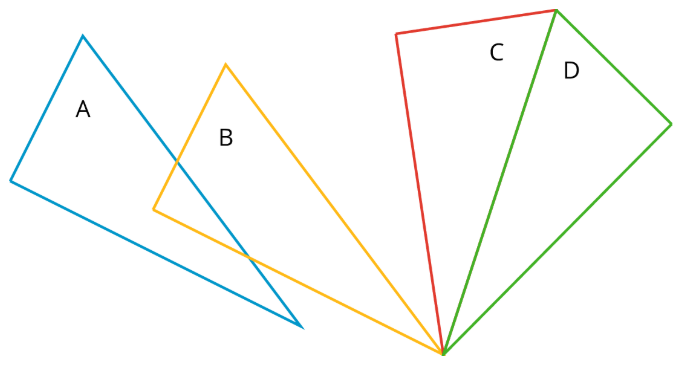
Una figura es congruente con otra si se puede mover con traslaciones, rotaciones y reflejos para encajar exactamente sobre la otra.

En la figura, el Triángulo A es congruente con los Triángulos B, C y D. Una traslación toma el Triángulo A al Triángulo B, una rotación toma el Triángulo B al Triángulo C y una reflexión lleva al Triángulo C al Triángulo D.

Definición: Ángulo recto

Un ángulo recto es la mitad de un ángulo recto. Mide 90 grados.

Practica

Ejercicio$\PageIndex{5}$

Demostrar que los dos pentágonos son congruentes.
Encuentra las longitudes laterales de$ABCDE$ y las medidas de ángulo de$FGHIJ$.

La figura J I H G F parece ser la imagen de la figura A B C D E después de una rotación y una traslación.

Ejercicio$\PageIndex{6}$

Para cada par de formas, decida si las dos formas son congruentes o no. Explica tu razonamiento.

Figura$\PageIndex{17}$: Dos cuadriláteros A B C D y E F G H en una cuadrícula cuadrada. Deje que la esquina inferior izquierda sea (0 coma 0). Entonces las coordenadas de A B C D son A (1 coma 3), B (2 coma 4), C (2 coma 5) y D (5 coma 5). Las coordenadas de E F G H son E (11 coma 1), F (10 coma 2), G (10 coma 3) y H (6 coma 3).

Figura$\PageIndex{18}$: Dos figuras A B C D E F y G H I J K L en un plano de coordenadas, origen O. Escala de eje horizontal negativa 7 a 6 por 1's. Escala de eje vertical negativa 3 a 4 por 1's. Las coordenadas de A B C D E F son A (negativo 6 coma 2), B (negativo 4 coma 2), C (negativo 4 coma negativo 2), D (negativo 2 coma), D (negativo 2 coma 3), E (negativo 4 coma 4) y F (negativo 7 coma 4). Las coordenadas de G H I J K L son G (0 coma negativa 1), H (5 coma negativa 3), I (6 coma negativa1), J (6 coma 2), K (4 coma 1) y L (4 coma 0).

Figura$\PageIndex{19}$: Dos círculos A y B en un plano de coordenadas, origen O. Escala del eje horizontal negativa 8 a 7 por 1's. Escala del eje vertical negativo 4 a 5 por 1's. El centro del círculo A es A (negativo 4 coma 2). El centro del círculo C es C (4 comas negativas 1). Ambos círculos tienen un diámetro de 2.

Ejercicio$\PageIndex{7}$

Segmento de dibujo$PQ$.
Cuando$PQ$ se gira$180^{\circ}$ alrededor del punto$R$, el segmento resultante es el mismo que$PQ$. ¿Dónde podría$R$ ubicarse el punto?

(De la Unidad 1.2.2)

Ejercicio$\PageIndex{8}$

Aquí hay un trapecio$ABCD$.

Usando transformaciones rígidas en el trapecio, construye un patrón. Describa algunas de las transformaciones rígidas que utilizó.

(De la Unidad 1.2.4)

Search

Text Color

Text Size

Margin Size

Font Type