6.1.1: Organizar datos
- Page ID
- 118743
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Lección
Busquemos formas de mostrar patrones en los datos
Ejercicio\(\PageIndex{1}\): Notice and Wonder: Messy Data
Aquí hay una tabla de datos. Cada fila muestra dos medidas de un triángulo.
| longitud del lado corto (cm) | longitud del perímetro (cm) |
|---|---|
| 0.25 | 1 |
| 2 | 7.5 |
| 6.5 | 22 |
| 3 | 9.5 |
| 0.5 | 2 |
| 1.25 | 3.5 |
| 3.5 | 12.5 |
| 1.5 | 5 |
| 4 | 14 |
| 1 | 2.5 |
¿Qué notas? ¿Qué te preguntas?
Ejercicio\(\PageIndex{2}\): Seeing the Data
Aquí está la tabla de medidas isósceles del triángulo rectángulo desde el calentamiento y una tabla vacía.
| longitud de lados cortos (cm) | longitud del perímetro (cm) | longitud de lados cortos (cm) | longitud del perímetro (cm) |
|---|---|---|---|
| 0.25 | 1 | ||
| 2 | 7.5 | ||
| 6.5 | 22 | ||
| 3 | 9.5 | ||
| 0.5 | 2 | ||
| 1.25 | 3.5 | ||
| 3.5 | 12.5 | ||
| 1.5 | 5 | ||
| 4 | 14 | ||
| 1 | 2.5 |
- ¿Cómo se pueden organizar las medidas desde la primera tabla para que cualquier patrón sea más fácil de ver? Escribe las medidas organizadas en la tabla vacía.
- Para cada una de las siguientes longitudes, estime el perímetro de un triángulo rectángulo isósceles cuyos lados cortos tengan esa longitud. Explica tu razonamiento para cada triángulo.
- la longitud de los lados cortos es de 0.75 cm
- la longitud de los lados cortos es de 5 cm
- la longitud de los lados cortos es de 10 cm
¿Estás listo para más?
Además de las representaciones gráficas de datos que has aprendido, hay otras que tienen sentido en otras situaciones. Examine los mapas que muestran los resultados de las elecciones para presidente de Estados Unidos para 2012 y 2016. En rojo están los estados donde se emitió la mayoría de votos electorados para el candidato republicano. En azul están los estados donde se emitió la mayoría de los votos del electorado para el candidato demócrata.
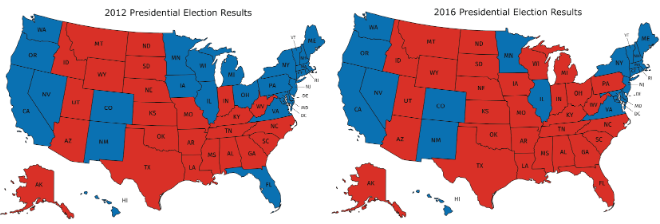
- ¿Qué información se puede ver en estos mapas que sería más difícil de ver en un gráfico de barras que muestre el número de votos electorados para los 2 principales candidatos?
- ¿Por qué estas representaciones son adecuadas para los datos que se muestran?
Ejercicio\(\PageIndex{3}\): Tables and Their Scatter Plots
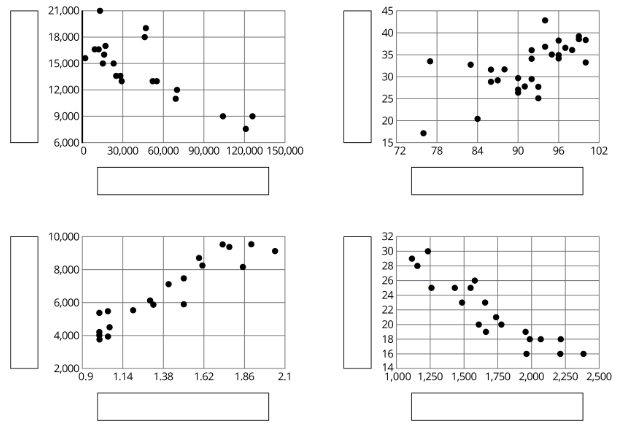
Aquí hay cuatro diagramas de dispersión. Tu profesor te dará cuatro tablas de datos.
- Coincidir cada tabla con una de las gráficas de dispersión.
- Utilice la información de las tablas para etiquetar los ejes para cada gráfica de dispersión.
Resumen
Considera los datos recopilados al tirar hacia atrás un carro de juguete y luego dejarlo avanzar. En la primera tabla, los datos pueden no parecer tener un patrón obvio. La segunda tabla tiene los mismos datos y muestra que ambos valores van aumentando juntos.
| distancia tirada hacia atrás (pulg) | distancia recorrida (in) |
|---|---|
| 8 | 23.57 |
| 4 | 18.48 |
| 10 | 38.66 |
| 8 | 31.12 |
| 2 | 13.86 |
| 1 | 8.95 |
| distancia tirada hacia atrás (pulg) | distancia recorrida (in) |
|---|---|
| 1 | 8.95 |
| 2 | 13.86 |
| 4 | 18.48 |
| 6 | 23.57 |
| 8 | 31.12 |
| 10 | 38.66 |
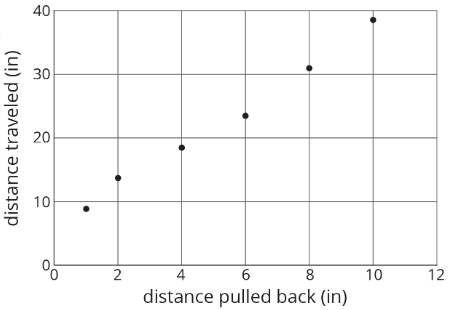
Un diagrama de dispersión de los datos hace que el patrón sea lo suficientemente claro como para que podamos estimar hasta dónde viajará el automóvil cuando se retroceda 5 pulgadas.
Los patrones en los datos a veces pueden volverse más obvios cuando se reorganizan en una tabla o cuando se representan en gráficos de dispersión u otros diagramas. Si se observa un patrón, a veces se puede utilizar para hacer predicciones.
Entradas en el glosario
Definición: Gráfica de dispersión
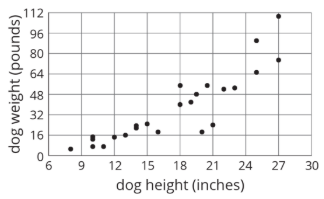
Una gráfica de dispersión es una gráfica que muestra los valores de dos variables en un plano de coordenadas. Nos permite investigar las conexiones entre las dos variables.
Cada punto trazado corresponde a un perro. Las coordenadas de cada punto nos indican la altura y el peso de ese perro.
Practica
Ejercicio\(\PageIndex{4}\)
Aquí hay datos sobre el número de casos de tos ferina de 1939 a 1955.
| año | número de casos |
|---|---|
| 1941 | 222,202 |
| 1950 | 120,718 |
| 1945 | 133,792 |
| 1942 | 191,383 |
| 1953 | 37,129 |
| 1939 | 103,188 |
| 1951 | 68,687 |
| 1948 | 74,715 |
| 1955 | 62,786 |
| 1952 | 45,030 |
| 1940 | 183,866 |
| 1954 | 60,866 |
| 1944 | 109,873 |
| 1946 | 109,860 |
| 1943 | 191,890 |
| 1949 | 69,479 |
| 1947 | 156,517 |
- Hacer una nueva tabla que ordene los datos por año.
- Encierra en círculo los años en tu mesa que tuvieron menos de 100 mil casos de tos ferina.
- Con base en estos datos, ¿esperaría que 1956 tuviera más cerca de 50 mil casos o más cerca de 100 mil casos?
Ejercicio\(\PageIndex{5}\)
En las estadísticas de voleibol, se registra un bloqueo cuando un jugador desvía la pelota golpeada del equipo contrario. Además, los anotadores suelen realizar un seguimiento del número promedio de bloqueos que un jugador registra en un juego. Aquí forma parte de una tabla que registra el número de bloqueos y bloqueos por juego para cada jugadora en un torneo de voleibol femenino. A continuación se muestra una gráfica de dispersión que va con la tabla.
| bloques | bloques por juego |
|---|---|
| 13 | 1.18 |
| 1 | 0.17 |
| 5 | 0.42 |
| 0 | 0 |
| 0 | 0 |
| 7 | 0.64 |
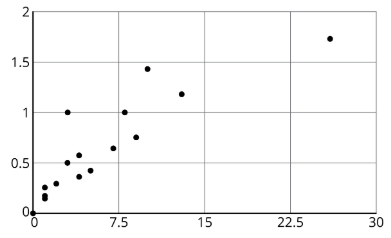
Etiquete los ejes de la gráfica de dispersión con la información necesaria.
Ejercicio\(\PageIndex{6}\)
Un cilindro tiene un radio de 4 cm y una altura de 5 cm.
- ¿Cuál es el volumen del cilindro?
- ¿Cuál es el volumen del cilindro cuando se triplica su radio?
- ¿Cuál es el volumen del cilindro cuando su radio está reducido a la mitad?
(De la Unidad 5.5.2)