7.2.5: ¿Qué pasa con otras bases?

Lección

Exploremos patrones de exponentes con bases distintas a 10.

Ejercicio\(\PageIndex{1}\): True or False: Comparing Expressions with Exponents

¿Cada afirmación es verdadera o falsa? Esté preparado para explicar su razonamiento.

1. \(3^{5}<4^{6}\)
2. \((-3)^{2}<3^{2}\)
3. \((-3)^{3}=3^{3}\)
4. \((-5)^{2}>-5^{2}\)

Ejercicio\(\PageIndex{2}\): What Happens with Zero and Negative Exponents?

Completa la tabla para mostrar lo que significa tener un exponente de cero o un exponente negativo.

Figura\(\PageIndex{1}\): Una mesa con dos filas. Primera fila, valor, 16, 4 espacios en blanco, fracción 1 sobre 2, tres espacios en blanco. Segunda fila, forma exponente, 2 a la cuarta potencia, 8 espacios en blanco. Encima de la fila superior, las flechas apuntan columna a columna de derecha a izquierda, etiquetadas tiempo 2. Debajo de la fila inferior, las flechas apuntan columna a columna, de izquierda a derecha, etiquetadas veces signo de interrogación.

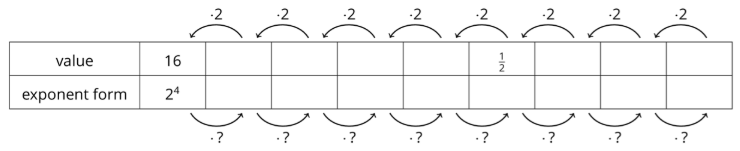
1. A medida que te mueves hacia la izquierda, cada número se multiplica por 2. ¿Cuál es el multiplicador a medida que avanzas hacia la derecha?
2. Usa los patrones que encontraste en la tabla para escribir\(2^{-6}\) como fracción.
3. Escribe\(\frac{1}{32}\) como una potencia de 2 con un solo exponente.
4. ¿Cuál es el valor de\(2^{0}\)?
5. Del trabajo que has realizado con exponentes negativos, ¿cómo escribirías\(5^{-3}\) como fracción?
6. ¿Cómo escribirías\(3^{-4}\) como fracción?

¿Estás listo para más?

1. Encuentra una expresión equivalente a\(\left(\frac{2}{3}\right)^{-3}\) pero con exponentes positivos.
2. Encuentra una expresión equivalente a\(\left(\frac{4}{5}\right)^{-8}\) pero con exponentes positivos.
3. ¿Qué patrones notas cuando comienzas con una fracción elevada a un exponente negativo y la reescribes usando un solo exponente positivo? Muestre o explique su razonamiento.

Ejercicio\(\PageIndex{3}\): Exponent Rules with Bases Other than 10

Lin, Noé, Diego y Elena deciden poner a prueba el conocimiento de cada uno de los exponentes con bases distintas a 10. Cada uno eligió una expresión para comenzar y luego se les ocurrió una nueva lista de expresiones; algunas de las cuales son equivalentes a la original y otras no.

Elige 2 de las 4 listas para analizar. Por cada lista de expresiones que elija analizar, decida qué expresiones no son equivalentes a la original. Esté preparado para explicar su razonamiento.

1. La expresión original de Lin es\(5^{-9}\) y su lista es:
   \[(5^{3})^{-3}\qquad -5^{9}\qquad \frac{5^{-6}}{5^{3}}\qquad(5^{3})^{-2}\qquad\frac{5^{-4}}{5^{-5}}\qquad 5^{-4}\cdot 5^{-5}\nonumber\]
2. La expresión original de Noé es\(3^{10}\) y su lista es:
   \[3^{5}\cdot 3^{2}\qquad (3^{5})^{2}\qquad (3\cdot 3)(3\cdot 3)(3\cdot 3)(3\cdot 3)\qquad \left(\frac{1}{3}\right)^{-10}\qquad 3^{7}\cdot 3^{3}\qquad\frac{3^{20}}{3^{10}}\qquad\frac{3^{20}}{3^{2}}\nonumber\]
3. La expresión original de Diego es\(x^{4}\) y su lista es:
   \[\frac{x^{8}}{x^{4}}\qquad x\cdot x\cdot x\cdot x\qquad\frac{x^{-4}}{x^{-8}}\qquad\frac{x^{-4}}{x^{8}}\qquad (x^{2})^{2}\qquad 4\cdot x\qquad x\cdot x^{3}\nonumber\]
4. La expresión original de Elena es\(8^{0}\) y su lista es:
   \[1\qquad 0\qquad 8^{3}\cdot 8^{-3}\qquad\frac{8^{2}}{8^{2}}\qquad 10^{0}\qquad 11^{0}\nonumber\]

Resumen

Anteriormente nos enfocamos en potencias de 10 porque 10 juega un papel especial en el sistema de números decimales. Pero las reglas de exponente que desarrollamos para 10 también funcionan para otras bases. Por ejemplo, si\(2^{0}=1\) y\(2^{-n}=\frac{1}{2^{n}}\), entonces

\[\begin{aligned}2^{m}\cdot 2^{n}&=2^{m+n}\\ (2^{m})^{n}&=2^{m\cdot n} \\ \frac{2^{m}}{2^{n}}&=2^{m-n}\end{aligned}\nonumber\]

Estas reglas también funcionan para poderes de números menores a 1. Por ejemplo,\(\left(\frac{1}{3}\right)^{2}=\frac{1}{3}\cdot\frac{1}{3}\) y\(\left(\frac{1}{3}\right)^{4}=\frac{1}{3}\cdot\frac{1}{3}\cdot\frac{1}{3}\cdot\frac{1}{3}\). También podemos comprobarlo\(\left(\frac{1}{3}\right)^{2}\cdot\left(\frac{1}{3}\right)^{4}=\left(\frac{1}{3}\right)^{2+4}\).

El uso de una variable\(x\) ayuda a ver esta estructura. Ya que\(x^{2}\cdot x^{5}=x^{7}\) (ambas partes tienen 7 factores que son\(x\)), si lo dejamos\(x=4\), podemos ver eso\(4^{2}\cdot 4^{5}=4^{7}\). Del mismo modo, podríamos dejar\(x=\frac{2}{3}\)\(x=11\) o cualquier otro valor positivo y demostrar que estas relaciones aún se mantienen.

Entradas en el glosario

Definición: Base (de un exponente)

En expresiones como\(5^{3}\) y\(8^{2}\), el 5 y el 8 se llaman bases. Te dicen qué factor multiplicar repetidamente. Por ejemplo,\(5^{3}=5\cdot 5\cdot 5\), y\(8^{2}=8\cdot 8\).

Practica

Ejercicio\(\PageIndex{4}\)

Priya dice “Puedo averiguarlo\(5^{0}\) mirando otros poderes de 5. \(5^{3}\)es 125,\(5^{2}\) es 25, entonces\(5^{1}\) es 5”.

1. ¿Qué patrón notas?
2. Si este patrón continúa, ¿cuál debería ser el valor de\(5^{0}\)? Explique cómo sabe.
3. Si este patrón continúa, ¿cuál debería ser el valor de\(5^{-1}\)? Explique cómo sabe.

Ejercicio\(\PageIndex{5}\)

Seleccione todas las expresiones que sean equivalentes a\(4^{-3}\).

1. \(-12\)
2. \(2^{-6}\)
3. \(\frac{1}{4^{3}}\)
4. \(\left(\frac{1}{4}\right)\cdot\left(\frac{1}{4}\right)\cdot\left(\frac{1}{4}\right)\)
5. \(12\)
6. \((-4)\cdot (-4)\cdot (-4)\)
7. \(\frac{8^{-1}}{2^{2}}\)

Ejercicio\(\PageIndex{6}\)

Escribe cada expresión usando un solo exponente.

1. \(\frac{5^{3}}{5^{6}}\)
2. \((14^{3})^{6}\)
3. \(8^{3}\cdot 8^{6}\)
4. \(\frac{16^{6}}{16^{3}}\)
5. \((21^{3})^{-6}\)

Ejercicio\(\PageIndex{7}\)

Andre establece un pluviómetro para medir la lluvia en su patio trasero. El martes llueve apagado y encendido todo el día.

• Comienza a las 10 de la mañana con un manómetro vacío cuando empieza a llover.
• Dos horas después, revisa, y el manómetro tiene 2 cm de agua en él.
• Comienza a llover aún más fuerte, y a las 4 de la tarde, la lluvia se detiene, por lo que Andre revisa el pluviómetro y encuentra que tiene 10 cm de agua en él.
• Mientras lo revisa, accidentalmente golpea el pluviómetro y derrama la mayor parte del agua, dejando solo 3 cm de agua en el pluviómetro.
• Cuando revisa por última vez a las 5 de la tarde, no hay cambio.

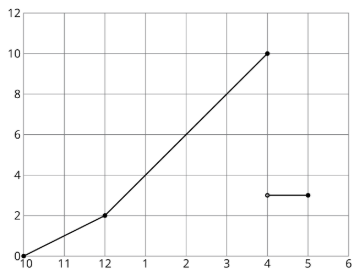
Gráfica A

Figura\(\PageIndex{2}\): Gráfico lineal, eje horizontal etiquetado 10, 11, 12, 1, 2, 3, 4, 5, 6. Vertical, 0 a 12 por 2. Segmentos, 10 coma 0 a 12 coma 2, luego a 4 coma 10, círculos cerrados. Un círculo abierto en 4 coma 3 se conecta a un círculo cerrado en 5 coma 3.

Gráfica B

Figura\(\PageIndex{3}\)

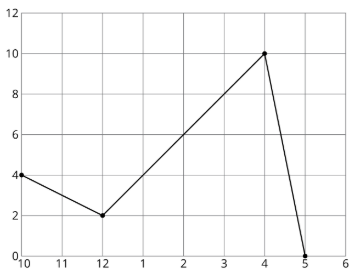
1. ¿Cuál de las dos gráficas podría representar la historia de Andre? Explica tu razonamiento.
2. Etiquete los ejes de la gráfica correcta con las unidades apropiadas.
3. Usa la gráfica para determinar cuánta lluvia total cayó el martes.

(De la Unidad 5.2.4)