7.2.4: Exponentes negativos con potencias de 10

Última actualización
Guardar como PDF

Page ID: 118786

Illustrative Mathematics
OpenUp Resources

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Lección

Veamos qué pasa cuando los exponentes son negativos.

Ejercicio$\PageIndex{1}$: Number Talk: What's That Exponent?

Resuelve cada ecuación mentalmente.

$\frac{100}{1}=10^{x}$

$\frac{100}{x}=10^{1}$

$\frac{x}{100}=10^{0}$

$\frac{10}{1000}=10^{x}$

Ejercicio$\PageIndex{2}$: Negative Exponent Table

Completa la tabla para explorar qué significan los exponentes negativos.

Figura$\PageIndex{1}$: Una mesa con tres filas. Fila superior, usando exponentes, 10 cubos, 10 cuadrados, 10 a la primera potencia, en blanco, en blanco, en blanco, en blanco, en blanco. Segunda fila, como decimal, 1000 punto 0, en blanco, en blanco, 1 punto 0, en blanco, 0 punto 0 1, en blanco. Tercera fila, como fracción, blanco, fracción 100 sobre 1, blanco, fracción 1 sobre 1, blanco, blanco, fracción 1 sobre mil. Encima de la fila, las flechas apuntan de columna a columna, de derecha a izquierda, cada una etiquetada por 10 veces. Debajo de la fila inferior, las flechas apuntan de columna a columna, de izquierda a derecha, cada una etiquetada signo de interrogación de tiempo.

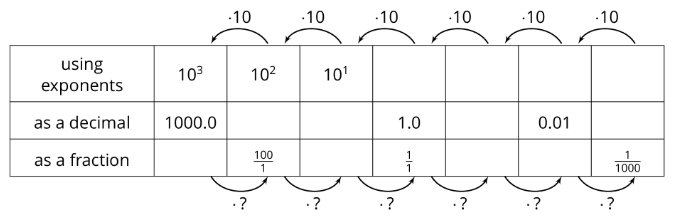
A medida que te mueves hacia la izquierda, cada número se multiplica por 10. ¿Cuál es el multiplicador mientras te mueves a la derecha?
¿Cómo afecta un multiplicador de 10 a la colocación del decimal en el producto? ¿Cómo afecta el otro multiplicador a la colocación del decimal en el producto?
Usa los patrones que encontraste en la tabla para escribir$10^{-7}$ como fracción.
Usa los patrones que encontraste en la tabla para escribir$10^{-5}$ como decimal.
Escribir$\frac{1}{100,000,000}$ usando un solo exponente.
Usa los patrones de la tabla para escribir$10^{-n}$ como fracción.

Ejercicio$\PageIndex{3}$: Follow the Exponential Rules

1. Haga coincidir cada expresión exponencial con una expresión de multiplicación equivalente:
  \[\begin{array}{lcl}{(10^{2})^{3}}&{\qquad}&{\frac{1}{(10\cdot 10}\cdot \frac{1}{(10\cdot 10}\cdot \frac{1}{(10\cdot 10} }\\{(10^{2})^{-3}}&{\qquad }&{\left(\frac{1}{10}\cdot\frac{1}{10}\right) \left(\frac{1}{10}\cdot\frac{1}{10}\right) \left(\frac{1}{10}\cdot\frac{1}{10}\right) }\\{(10^{-2})^{3}}&{\qquad }&{\frac{1}{\frac{1}{10}\cdot\frac{1}{10}}\cdot \frac{1}{\frac{1}{10}\cdot\frac{1}{10}}\cdot \frac{1}{\frac{1}{10}\cdot\frac{1}{10}} }\\{(10^{-2})^{-3}}&{\qquad}&{(10\cdot 10)(10\cdot 10)(10\cdot 10)}\end{array}\nonumber\]
2. Escribe$(10^{2})^{-3}$ como una potencia de 10 con un solo exponente. Esté preparado para explicar su razonamiento.
1. Haga coincidir cada expresión exponencial con una expresión de multiplicación equivalente:
  \[\begin{array}{lcl}{\frac{10^{2}}{10^{5}}}&{\qquad}&{\frac{\frac{1}{10}\cdot\frac{1}{10}}{\frac{1}{10}\cdot\frac{1}{10}\cdot\frac{1}{10}\cdot\frac{1}{10}\cdot\frac{1}{10}}}\\{\frac{10^{2}}{10^{-5}}}&{\qquad}&{\frac{10\cdot 10}{10\cdot 10\cdot 10\cdot 10\cdot 10}}\\{\frac{10^{-2}}{10^{5}}}&{\qquad}&{\frac{\frac{1}{10}\cdot\frac{1}{10}}{10\cdot 10\cdot 10\cdot 10\cdot 10}}\\{\frac{10^{-2}}{10^{-5}}}&{\qquad}&{\frac{10\cdot 10}{\frac{1}{10}\cdot\frac{1}{10}\cdot\frac{1}{10}\cdot\frac{1}{10}\cdot\frac{1}{10}}}\end{array}\nonumber\]
2. Escribe$\frac{10^{-2}}{10^{-5}}$ como una potencia de 10 con un solo exponente. Esté preparado para explicar su razonamiento.
1. Haga coincidir cada expresión exponencial con una expresión de multiplicación equivalente:
2. \[\begin{array}{lcl}{10^{4}\cdot 10^{3}}&{\qquad}&{(10\cdot 10\cdot 10\cdot 10)\cdot \left(\frac{1}{10}\cdot \frac{1}{10}\cdot \frac{1}{10}\right)}\\{10^{4}\cdot 10^{-3}}&{\qquad }&{\left(\frac{1}{10}\cdot \frac{1}{10}\cdot\frac{1}{10}\cdot\frac{1}{10}\right)\cdot\left(\frac{1}{10}\cdot\frac{1}{10}\cdot\frac{1}{10}\right)}\\{10^{-4}\cdot 10^{3}}&{\qquad }&{\left(\frac{1}{10}\cdot\frac{1}{10}\cdot\frac{1}{10}\frac{1}{10}\right)\cdot (10\cdot 10\cdot 10) }\\{10^{-4}\cdot 10^{-3}}&{\qquad}&{(10\cdot 10\cdot 10\cdot 10)\cdot (10\cdot 10\cdot 10)}\end{array}\nonumber\]
3. Escribe$10^{-4}\cdot 10^{3}$ como una potencia de 10 con un solo exponente. Esté preparado para explicar su razonamiento.

¿Estás listo para más?

Priya, Jada, Han y Diego se paran en círculo y se turnan para jugar un juego.

Dice Priya, SEGURO. Jada, de pie a la izquierda de Priya, dice, FUERA y deja el círculo. Han es el siguiente: dice, SEGURO. Entonces Diego dice, OUT y deja el círculo. En este punto, solo quedan Priya y Han. Siguen alternando. Dice Priya, SEGURO. Han dice, OUT y deja el círculo. Priya es la única persona que queda, por lo que es la ganadora.

Priya dice: “Sabía que sería el único que me quedaría, ya que fui primero”.

Graba este juego en papel varias veces con diferentes números de jugadores. ¿Siempre gana la persona que empieza?
Intenta encontrar tantos números como puedas donde siempre gana la persona que empieza. ¿Qué patrones notas?

Resumen

Cuando multiplicamos una potencia positiva de 10 por$\frac{1}{10}$, el exponente disminuye en 1:$10^{8}\cdot\frac{1}{10}=10^{7}$ Esto es cierto para cualquier potencia positiva de 10. Podemos razonar de manera similar que multiplicando por 2 factores que son$\frac{1}{10}$ disminuye el exponente por 2:$\left(\frac{1}{10}\right)^{2}\cdot 10^{8}=10^{6}$

Eso significa que podemos extender las reglas para usar exponentes negativos si hacemos$10^{-2}=\left(\frac{1}{10}\right)^{2}$. Así como$10^{2}$ son dos factores que son 10, tenemos que$10^{-2}$ son dos factores que son$\frac{1}{10}$. De manera más general, las reglas de exponente que hemos desarrollado son ciertas para cualquier número entero$n$ y$m$ si hacemos$10^{-n}=\left(\frac{1}{10}\right)^{n}=\frac{1}{10^{n}}$

Aquí un ejemplo de extender la regla$\frac{10^{n}}{10^{m}}=10^{n-m}$ para usar exponentes negativos:$\frac{10^{3}}{10^{5}}=10^{3-5}=10^{-2}$ Para ver por qué, observe$\frac{10^{3}}{10^{5}}=\frac{10^{3}}{10^{3}\cdot 10^{2}}=\frac{10^{3}}{10^{3}}\cdot\frac{1}{10^{2}}=\frac{1}{10^{2}}$ lo que es igual a$10^{-2}$.

Aquí un ejemplo de extender la regla$(10^{m})^{n}=10^{m\cdot n}$ para usar exponentes negativos:$(10^{-2})^{3}=10^{(-2)(3)}=10^{-6}$ Para ver por qué, fíjate en eso$10^{-2}=\frac{1}{10}\cdot\frac{1}{10}$. Esto significa que$(10^{-2})^{3}=\left(\frac{1}{10}\cdot\frac{1}{10}\right) ^{3}=\left(\frac{1}{10}\cdot\frac{1}{10}\right) \cdot \left(\frac{1}{10}\cdot\frac{1}{10}\right) \cdot \left(\frac{1}{10}\cdot\frac{1}{10}\right) =\frac{1}{10^{6}}=10^{-6}$

Entradas en el glosario

Definición: Base (de un exponente)

En expresiones como$5^{3}$ y$8^{2}$, el 5 y el 8 se llaman bases. Te dicen qué factor multiplicar repetidamente. Por ejemplo,$5^{3}=5\cdot 5\cdot 5$, y$8^{2}=8\cdot 8$.

Practica

Ejercicio$\PageIndex{4}$

Escribir con un solo exponente: (ex:$\frac{1}{10}\cdot\frac{1}{10}=10^{-2})$

$\frac{1}{10}\cdot\frac{1}{10}\cdot\frac{1}{10}$
$\frac{1}{10}\cdot\frac{1}{10}\cdot\frac{1}{10}\cdot \frac{1}{10}\cdot\frac{1}{10}\cdot\frac{1}{10}\cdot\frac{1}{10}$
$\left(\frac{1}{10}\cdot\frac{1}{10}\cdot\frac{1}{10}\cdot\frac{1}{10}\right)^{2}$
$\left(\frac{1}{10}\cdot\frac{1}{10}\cdot\frac{1}{10}\right)^{3}$
$(10\cdot 10\cdot 10)^{-2}$

Ejercicio$\PageIndex{5}$

Escribe cada expresión como una sola potencia de 10.

$10^{-3}\cdot 10^{-2}$
$10^{4}\cdot 10^{-1}$
$\frac{10^{5}}{10^{7}}$
$\left(10^{-4}\right) ^{5}$
$10^{-3}\cdot 10^{2}$
$\frac{10^{-9}}{10^{5}}$

Ejercicio$\PageIndex{6}$

Seleccione todas las siguientes opciones que sean equivalentes a$\frac{1}{10,000}$:

$(10,000)^{-1}$
$(-10,000)$
$(100)^{-2}$
$(10)^{-4}$
$(-10)^{2}$

Ejercicio$\PageIndex{7}$

Haga coincidir cada ecuación con la situación que describe. Explicar qué significa la constante de proporcionalidad en cada ecuación.

Ecuaciones:

$y=3x$
$\frac{1}{2}x=y$
$y=3.5x$
$y=\frac{5}{2}x$

Situaciones:

Un camión volquete está transportando cargas de tierra a un sitio de construcción. Después de 20 cargas, hay 70 pies cuadrados de tierra.
Estoy haciendo una mezcla de agua y sal que tiene 2 tazas de sal por cada 6 tazas de agua.
Una tienda tiene una venta “4 por $10” en sombreros.
Por cada 48 galletas que horneo, mis alumnos obtienen 24.

(De la Unidad 3.1.2)

Ejercicio$\PageIndex{8}$

1. Explica por qué$ABC$ el triángulo es similar a$EDC$.

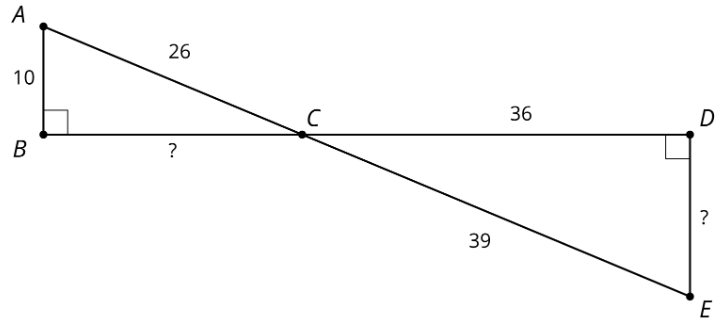
2. Encuentra las longitudes laterales faltantes.

(De la Unidad 2.2.3)

Search

Text Color

Text Size

Margin Size

Font Type