7.2.7: Combinar bases

Última actualización
Guardar como PDF

Page ID: 118792

Illustrative Mathematics
OpenUp Resources

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Lección

Multipliquemos expresiones con diferentes bases.

Ejercicio$\PageIndex{1}$: Same Exponent, Different Base

Evaluar$5^{3}\cdot 2^{3}$
Evaluar$10^{3}$

Ejercicio$\PageIndex{2}$: Power of Products

La tabla contiene productos de expresiones con diferentes bases y el mismo exponente. Completa la tabla para ver cómo podemos reescribirlos. Utilice la columna “expandida” para averiguar cómo combinar los factores en una nueva base.

Mesa$\PageIndex{1}$
expresión	ampliado	exponente
$5^{3}\cdot 2^{3}$	$\begin{aligned}(5\cdot 5\cdot 5)\cdot (2\cdot 2\cdot 2)&=(5\cdot 2)(5\cdot 2)(5\cdot 2) \\ &=10\cdot 10\cdot 10\end{aligned}$	$10^{3}$
$3^{2}\cdot 7^{2}$		$21^{2}$
$2^{4}\cdot 3^{4}$
		$15^{3}$
		$30^{4}$
$2^{4}\cdot x^{4}$
$a^{n}\cdot b^{n}$
$7^{4}\cdot 2^{4}\cdot 5^{4}$

¿Se puede escribir$2^{3}\cdot 3^{4}$ con un solo exponente? ¿Qué pasa si ni los exponentes ni las bases son iguales? Explica o muestra tu razonamiento.

Ejercicio$\PageIndex{3}$: How Many Ways Can You Make 3,600?

Tu profesor le dará a tu grupo herramientas para crear una pantalla visual para jugar un juego. Divide la pantalla en 3 columnas, con estos encabezados:

\[a^{n}\cdot a^{m}=a^{n+m}\qquad \frac{a^{n}}{a^{m}}=a^{n-m}\qquad a^{n}\cdot b^{n}=(a\cdot b)^{n}\nonumber\]

Cómo jugar:

Cuando comience el tiempo, usted y su grupo escribirán tantas expresiones como sea posible que equivalgan a un número específico usando una de las reglas de exponente en su tablero. Cuando se acabe el tiempo, compara tus expresiones con otro grupo para ver cuántos puntos ganas.

Tu grupo obtiene 1 punto por cada expresión única que escribas que es igual al número y sigue la regla de exponente que reclamaste.
Si una expresión usa exponentes negativos, obtienes 2 puntos en lugar de solo 1.
Puedes desafiar la expresión del otro grupo si crees que no es igual al número o si no sigue una de las tres reglas de exponente.

¿Estás listo para más?

Probablemente hayas notado que cuando cuadras un número impar, obtienes otro número impar, y cuando cuadras un número par, obtienes otro número par. Aquí hay una manera de ampliar el concepto de par e impar para el número 3. Cada entero es divisible por 3, uno más de un múltiplo de 3, o uno menor que un múltiplo de 3.

Ejemplos de números que son uno más que un múltiplo de 3 son 4, 7 y 25. Dar tres ejemplos más.
Ejemplos de números que son uno menos que un múltiplo de 3 son 2, 5 y 32. Dar tres ejemplos más.
¿Crees que es cierto que cuando cuadras un número que es un múltiplo de 3, tu respuesta seguirá siendo un múltiplo de 3? ¿Qué tal para las otras dos categorías? Intenta cuadrar algunos números para verificar tus conjeturas.

Resumen

Antes de esta lección, hicimos reglas para multiplicar y dividir expresiones con exponentes que solo funcionan cuando las expresiones tienen la misma base. Por ejemplo,$10^{3}\cdot 10^{2}=10^{5}$ o$2^{6}\div 2^{2}=2^{4}$

En esta lección, estudiamos cómo combinar expresiones con el mismo exponente, pero diferentes bases. Por ejemplo, podemos escribir$2^{3}\cdot 5^{3}$ como$2\cdot 2\cdot 2\cdot 5\cdot 5\cdot 5$. Reagrupar esto como$(2\cdot 5)\cdot (2\cdot 5)\cdot (2\cdot 5)$ muestra que

\[\begin{aligned} 2^{3}\cdot 5^{3}&= (2\cdot 5)^{3} \\ &=10^{3}\end{aligned}\nonumber\]

Observe que los 2 y 5 del ejemplo anterior podrían ser reemplazados por diferentes números o incluso variables. Por ejemplo, si$a$ y$b$ son variables entonces$a^{3}\cdot b^{3}=(a\cdot b)^{3}$. De manera más general, para un número positivo$n$,$a^{n}\cdot b^{n}=(a\cdot b)^{n}$ porque ambas partes tienen exactamente$n$ factores que son$a$ y$n$ factores que son$b$.

Entradas en el glosario

Definición: Base (de un exponente)

En expresiones como$5^{3}$ y$8^{2}$, los 5 y 8 se llaman bases. Te dicen qué factor multiplicar repetidamente. Por ejemplo,$5^{3}=5\cdot 5\cdot 5$, y$8^{2}=8\cdot 8$.

Definición: Recíproco

Dividir 1 por un número da el recíproco de ese número. Por ejemplo, el recíproco de 12 es$\frac{1}{12}$, y el recíproco de$\frac{2}{5}$ es$\frac{5}{2}$.

Practica

Ejercicio$\PageIndex{4}$

Seleccione todas las declaraciones verdaderas:

$2^{8}\cdot 2^{9}=2^{17}$
$8^{2}\cdot 9^{2}=72^{2}$
$8^{2}\cdot 9^{2}=72^{4}$
$2^{8}\cdot 2^{9}=4^{17}$

Ejercicio$\PageIndex{5}$

Encontrar$x$,$y$, y$x$ si$(3\cdot 5)^{4}\cdot (2\cdot 3)^{5}\cdot (2\cdot 5)^{7}=2^{x}\cdot 3^{y}\cdot 5^{z}$.

Ejercicio$\PageIndex{6}$

Han encontró una manera de calcular expresiones complicadas con mayor facilidad. Ya que$2\cdot 5=10$, busca emparejamientos de 2s y 5s que sabe igual a 10. Por ejemplo,$3\cdot 2^{4}\cdot 5^{5}=3\cdot 2^{4}\cdot 5^{4}\cdot 5=(3\cdot 5)\cdot (2\cdot 5)^{4}=15\cdot 10^{4}=150,000$ Use la técnica de Han para calcular lo siguiente:

$2^{4}\cdot 5\cdot (3\cdot 5)^{3}$
$\frac{2^{3}\cdot 5^{2}\cdot (2\cdot 3)^{2}\cdot (3\cdot 5)^{2}}{3^{2}}$

Ejercicio$\PageIndex{7}$

El costo del queso en tres tiendas es una función del peso del queso. El queso no está preenvasado, por lo que un cliente puede comprar cualquier cantidad de queso.

Tienda A vende el queso por$a$ dólares por libra.
Tienda B vende el mismo queso por$b$ dólares por libra y un cliente tiene un cupón por $5 de descuento en la compra total en esa tienda.
Store C es una tienda en línea, que vende el mismo queso a$c$ dólar por libra, pero con una tarifa de entrega de $10.

Esta gráfica muestra las funciones de precios de las tiendas A, B y C.

Figura$\PageIndex{1}$: Plano coordinado, horizontal, peso del queso en libras, 0 a 12 por 2, vertical, costo en dólares, 0 a 40 por 10. Línea j, de 0 coma 10 a 13 punto 5 a 50. Línea l, origen a 12 punto 5. Línea k de 1 coma 0 a 11 coma 60. Las líneas j y l se encuentran en 10 coma 40, las líneas k y l se encuentran en 5 coma 20, las líneas j y k se encuentran en 7 coma 35.

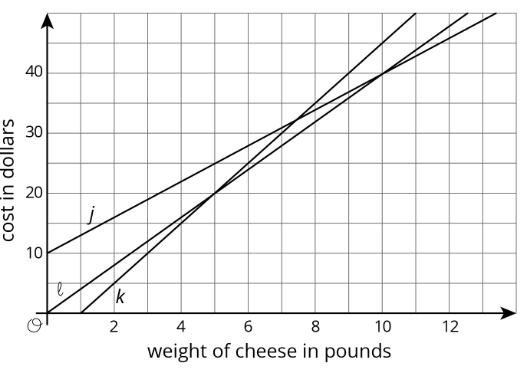
Coincidir las tiendas A, B, y C con gráficas$j$,$k$, y$l$.
¿Cuánto cobra cada tienda por el queso por libra?
¿Cuántas libras de queso paga el cupón de la Tienda B?
¿Qué tienda tiene el precio más bajo por media libra de queso?
Si un cliente quiere comprar 5 libras de queso para una fiesta, ¿qué tienda tiene el precio más bajo?
¿Cuántas libras necesitaría un cliente para ordenar para hacer de Store C una buena opción?

(De la Unidad 5.3.1)

expresión	ampliado	exponente
\(5^{3}\cdot 2^{3}\)	\(\begin{aligned}(5\cdot 5\cdot 5)\cdot (2\cdot 2\cdot 2)&=(5\cdot 2)(5\cdot 2)(5\cdot 2) \\ &=10\cdot 10\cdot 10\end{aligned}\)	\(10^{3}\)
\(3^{2}\cdot 7^{2}\)		\(21^{2}\)
\(2^{4}\cdot 3^{4}\)
		\(15^{3}\)
		\(30^{4}\)
\(2^{4}\cdot x^{4}\)
\(a^{n}\cdot b^{n}\)
\(7^{4}\cdot 2^{4}\cdot 5^{4}\)