Saltar al contenido principal
LibreTexts Español

1.1.3: Realización de Copias Escaladas

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    119234

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Lección

    Dibujemos copias a escala.

    Ejercicio\(\PageIndex{1}\): More or Less?

    Para cada problema, seleccione la respuesta entre las dos opciones.

    1. El valor de\(25\cdot (8.5)\) es:
      1. Más de 205
      2. Menos de 205
    2. El valor de\((9.93)\cdot (0.984)\) es:
      1. Más de 10
      2. Menos de 10
    3. El valor de\((0.24)\cdot (0.67)\) es:
      1. Más de 0.2
      2. Menos de 0.2

    Ejercicio\(\PageIndex{2}\): Drawing Scaled Copies

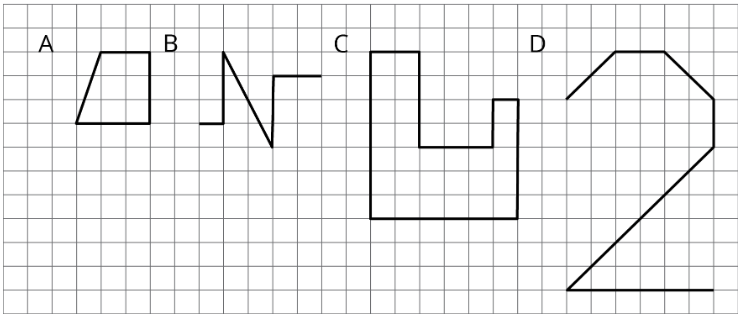
    clipboard_eaa2040aa3fbd68cf96a837b6ab3e3c7d.png
    Figura\(\PageIndex{1}\)
    1. Dibuje una copia a escala de la Figura A o B usando un factor de escala de\(3\).
    2. Dibuje una copia a escala de la Figura C o D usando un factor de escala de\(\frac{1}{2}\).

    Ejercicio\(\PageIndex{3}\): Which Operations? (Part 1)

    Diego y Jada quieren escalar este polígono por lo que el lado que corresponde a 15 unidades en el original es de 5 unidades en la copia a escala.

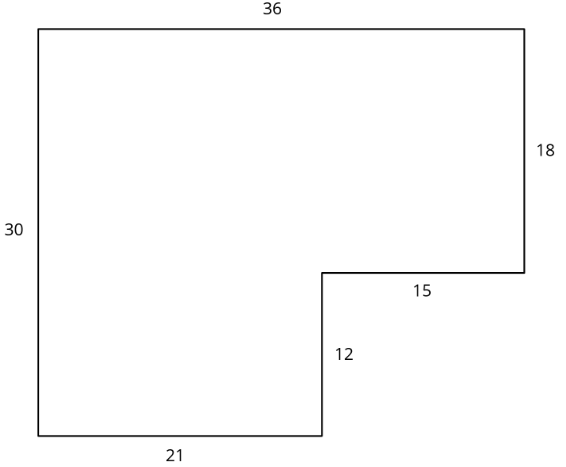
    clipboard_ecf61ffd17673a7acab0d2954e8035289.png
    Figura\(\PageIndex{2}\)

    Diego y Jada utilizan cada uno una operación diferente para encontrar las nuevas longitudes laterales. Aquí están sus dibujos terminados.

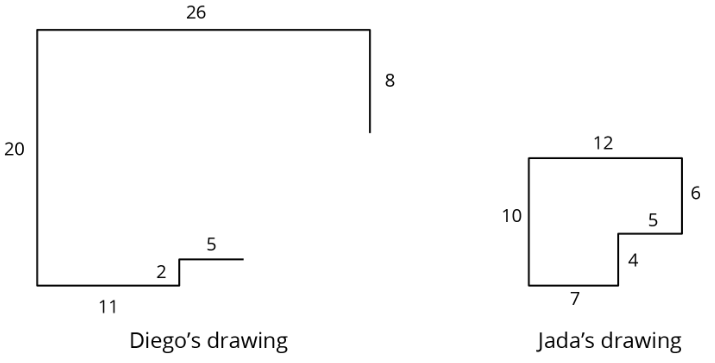
    clipboard_e8c99a8e7886ffb34d96574a8d7c38f9e.png
    Figura\(\PageIndex{3}\)
    1. ¿Qué operación crees que utilizó Diego para calcular los largos para su dibujo?
    2. ¿Qué operación crees que utilizó Jada para calcular los largos para su dibujo?
    3. ¿Cada método produjo una copia escalada del polígono? Explica tu razonamiento.

    Ejercicio\(\PageIndex{4}\): Which Operations? (Part 2)

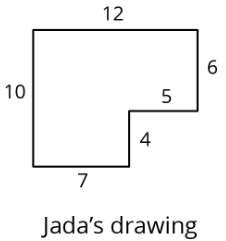
    Andre quiere hacer una copia a escala del dibujo de Jada así que el lado que corresponde a 4 unidades en el polígono de Jada es de 8 unidades en su copia a escala.

    1. Andre dice “Me pregunto si debería agregar 4 unidades a las longitudes de todos los segmentos?” ¿Qué dirías en respuesta a Andre? Explica o muestra tu razonamiento.
    2. Crea la copia a escala que Andre quiere. Si te atascas, considera usar el borde de una tarjeta de índice o papel para medir los largos necesarios para dibujar la copia.
    clipboard_edf4221b66671dfd846bdd383893e1e63.png
    Figura\(\PageIndex{4}\)

    ¿Estás listo para más?

    Las longitudes laterales del Triángulo B son todas 5 más que las longitudes laterales del Triángulo A. ¿Puede el Triángulo B ser una copia a escala del Triángulo A? Explica tu razonamiento.

    Resumen

    Crear una copia a escala implica multiplicar las longitudes de la figura original por un factor de escala.

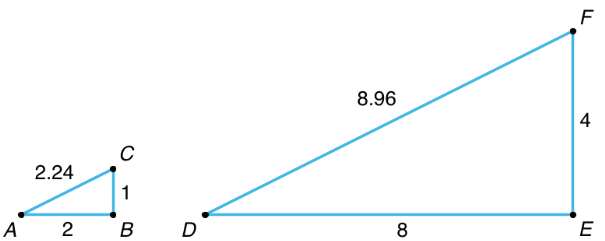
    Por ejemplo, para hacer una copia escalada de triángulo\(ABC\) donde la base es de 8 unidades, usaríamos un factor de escala de 4. Esto significa multiplicar todas las longitudes de los lados por 4, por lo que en triángulo\(DEF\), cada lado es 4 veces más largo que el lado correspondiente en triángulo\(ABC\).

    clipboard_ecf8e710ef213fe0548db9ed0ffc6e270.png
    Figura\(\PageIndex{5}\)

    Entradas en el glosario

    Definición: Correspondiente

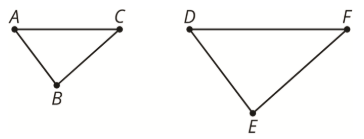
    Cuando parte de una figura original coincide con parte de una copia, las llamamos partes correspondientes. Estos podrían ser puntos, segmentos, ángulos o distancias.

    Por ejemplo, el punto\(B\) en el primer triángulo corresponde al punto\(E\) en el segundo triángulo. Segmento\(AC\) corresponde al segmento\(DF\).

    clipboard_e2728b3247bf3bb939a001aa3dc3bac53.png
    Figura\(\PageIndex{6}\)

    Definición: Factor de Escala

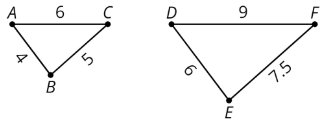
    Para crear una copia a escala, multiplicamos todas las longitudes de la figura original por el mismo número. A este número se le llama factor de escala.

    En este ejemplo, el factor de escala es 1.5, porque\(4\cdot (1.5)=6\),\(5\cdot (1.5)=7.5\), y\(6\cdot (1.5)=9\).

    clipboard_e919f0ad3848582ce451f8d8df95d9f1e.png
    Figura\(\PageIndex{7}\)

    Definición: Copia escalada

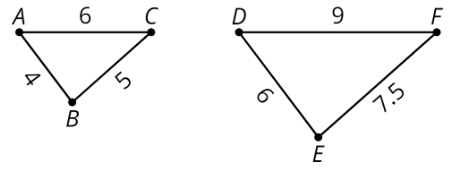
    Una copia a escala es una copia de una figura donde cada longitud de la figura original se multiplica por el mismo número.

    Por ejemplo, triángulo\(DEF\) es una copia a escala de triángulo\(ABC\). Cada longitud de lado en triángulo\(ABC\) se multiplicó por 1.5 para obtener la longitud de lado correspondiente en triángulo\(DEF\).

    clipboard_e7a834304f2fbd754976975695baf4ec5.png
    Figura\(\PageIndex{8}\)

    Practica

    Ejercicio\(\PageIndex{5}\)

    Aquí hay 3 polígonos.

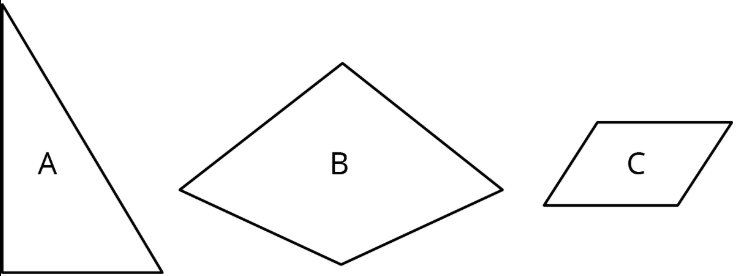
    clipboard_e1f45142655ce47692b68319789d966fc.png
    Figura\(\PageIndex{9}\)

    Dibuja una copia a escala del Polígono A usando un factor de escala de 2.

    Dibuja una copia a escala del Polígono B usando un factor de escala de\(\frac{1}{2}\).

    Dibuja una copia a escala del Polígono C usando un factor de escala de\(\frac{3}{2}\).

    Ejercicio\(\PageIndex{6}\)

    El cuadrilátero A tiene longitudes laterales 6, 9, 9 y 12. El cuadrilátero B es una copia a escala del cuadrilátero A, con su lado más corto de longitud 2. ¿Cuál es el perímetro del cuadrilátero B?

    Ejercicio\(\PageIndex{7}\)

    Aquí hay un polígono en una cuadrícula.

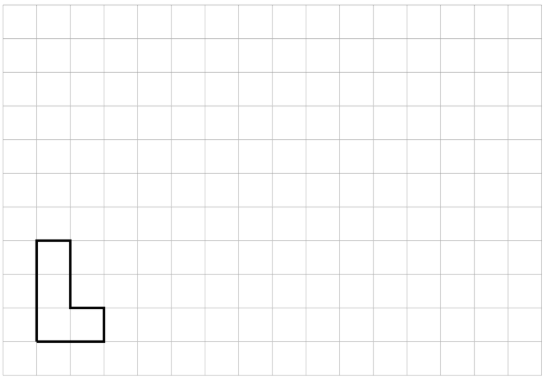
    clipboard_e691b8f2acf02260a76910c3f68418409.png
    Figura\(\PageIndex{10}\): Una figura en forma de L sobre una rejilla cuadrada. El polígono está compuesto por dos formas: un rectángulo unido con un cuadrado para que la base horizontal inferior del polígono sea de 2 unidades. El rectángulo tiene 1 unidad de ancho y 3 unidades de longitud. El cuadrado es de 1 unidad de ancho y 1 unidad de largo.

    Dibuja una copia a escala de este polígono que tenga un perímetro de 30 unidades. ¿Cuál es el factor de escala? Explique cómo sabe.

    Ejercicio\(\PageIndex{8}\)

    Priya y Tyler están discutiendo las cifras que se muestran a continuación. Priya piensa que B, C y D son copias a escala de A. Tyler dice que B y D son copias a escala de A. ¿Estás de acuerdo con Priya, o estás de acuerdo con Tyler? Explica tu razonamiento.

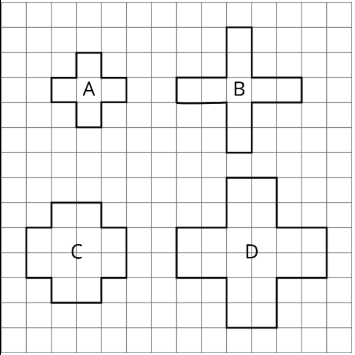
    clipboard_ea6d9cc1ff71c43a90f777b5816a9425f.png
    Figura\(\PageIndex{11}\): Cuatro formas que parecen signos más. La forma A es un cuadrado con un cuadrado agregado a cada lado. La forma B es un cuadrado con un rectángulo de 1 por 2 anexado a cada lado. La forma C es un cuadrado de 2 por 2 con un rectángulo de 1 por 2 agregado a cada lado. La forma D es un cuadrado de 2 por 2 con un cuadrado de 2 por 2 agregado a cada lado.

    (De la Unidad 1.1.1)

    This page titled 1.1.3: Realización de Copias Escaladas is shared under a CC BY license and was authored, remixed, and/or curated by Illustrative Mathematics.