Saltar al contenido principal
LibreTexts Español

1.2.3: Creación de dibujos a escala

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    119315

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Lección

    Vamos a crear nuestros propios dibujos a escala.

    Ejercicio\(\PageIndex{1}\): Number Talk: Which is Greater?

    Sin calcular, decide qué cociente es mayor.

    \(11\div 23\)o\(7\div 13\)

    \(0.63\div 2\)o\(0.55\div 3\)

    \(15\div\frac{1}{3}\)o\(15\div\frac{1}{4}\)

    Ejercicio\(\PageIndex{2}\): Bedroom Floor Plan

    Aquí hay un boceto aproximado del dormitorio de Noé (no un dibujo a escala).

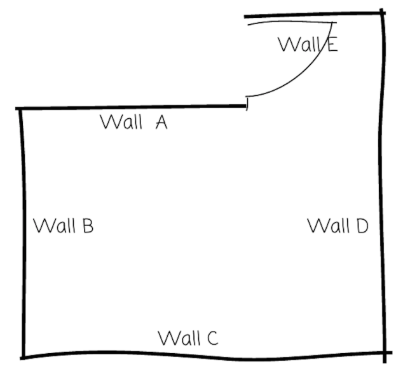
    clipboard_eade0a5eec0eea91f7b7c1c15a961d1af.png
    Figura\(\PageIndex{1}\)

    Noah quiere crear un plano de planta que sea un dibujo a escala.

    1. La longitud real del Muro C es de 4 m. Para representar el Muro C, Noé dibuja un segmento de 16 cm de largo. ¿Qué escala está usando? Explica o muestra tu razonamiento.
    2. Encuentra otra forma de expresar la báscula.
    3. Discuta tu pensamiento con tu pareja. ¿Cómo se comparan tus básculas?
    4. Las longitudes reales de la Pared A, la Pared B y la Pared D son de 2.5 m, 2.75 m y 3.75 m. Determine la duración de estas paredes en el plano de planta de la escala de Noé.
    5. Utilice la herramienta Punto
    clipboard_e6c6bd8696642b6da17db50d13d56a683.png
    Figura\(\PageIndex{2}\)

    y la herramienta Segmento

    clipboard_e3a48bf4f555a231e4cae8c9db4e93bcc.png
    Figura\(\PageIndex{3}\)

    para dibujar las paredes del plano de planta a escala de Noé en el applet.

    ¿Estás listo para más?

    Si Noé quisiera dibujar otro plano de planta en el que el Muro C tuviera 20 cm, ¿sería de 1 cm a 5 m la escala adecuada para usar? Explica tu razonamiento.

    Ejercicio\(\PageIndex{3}\): Two Maps of Utah

    Un rectángulo alrededor de Utah tiene aproximadamente 270 millas de ancho y aproximadamente 350 millas de alto. La esquina superior derecha que falta tiene unas 110 millas de ancho y unas 70 millas de altura.

    1. Haz un dibujo a escala de Utah donde 1 centímetro representa 50 millas.
      Haz un dibujo a escala de Utah donde 1 centímetro representa 75 millas.
    2. ¿Cómo se comparan los dos dibujos? ¿Cómo influye la elección de escala en el dibujo?

    Resumen

    Si queremos crear un dibujo a escala del plano de planta de una habitación que tenga la escala de “1 pulgada a 4 pies”, podemos dividir las longitudes reales en la habitación (en pies) por 4 para encontrar las longitudes correspondientes (en pulgadas) para nuestro dibujo.

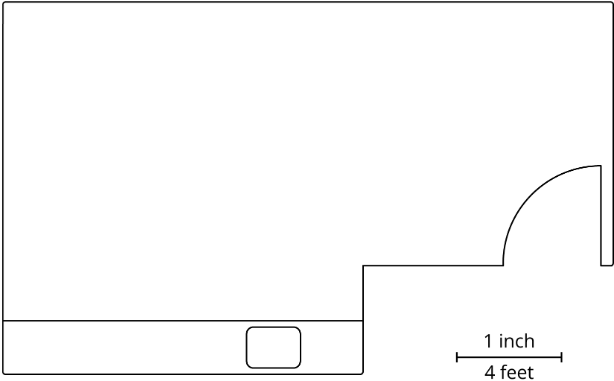
    clipboard_eb23b4b86463474dd72984ab0f2538560.png
    Figura\(\PageIndex{4}\)

    Supongamos que la pared más larga tiene 15 pies de largo. Deberíamos trazar una línea de 3.75 pulgadas de largo para representar este muro, porque\(15\div 4=3.75\).

    Hay más de una manera de expresar esta escala. Estas tres escalas son todas equivalentes, ya que representan la misma relación entre longitudes en un dibujo y longitudes reales:

    • \(1\)inch (pulgada) a\(4\) pies
    • \(\frac{1}{2}\)inch (pulgada) a\(2\) pies
    • \(\frac{1}{4}\)inch (pulgada) a\(1\) pie

    Cualquiera de estas escalas se puede utilizar para encontrar longitudes reales y longitudes escaladas (longitudes en un dibujo). Por ejemplo, podemos decir que, en esta escala, una pared de 8 pies de largo debería tener 2 pulgadas de largo en el dibujo porque\(\frac{1}{4}\cdot 8=2\).

    El tamaño de un dibujo a escala está influenciado por la elección de la escala. Por ejemplo, aquí hay otro dibujo a escala de la misma habitación usando la escala de 1 pulgada a 8 pies.

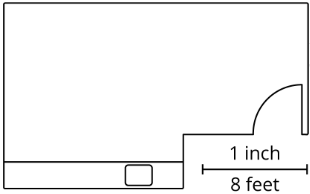
    clipboard_e4034115bcc29fdf338bf7011f1baee3c.png
    Figura\(\PageIndex{5}\)

    Observe que este dibujo es más pequeño que el anterior. Dado que una pulgada en este dibujo representa el doble de distancia real, la longitud de cada lado solo necesita ser la mitad de la larga que en el primer dibujo a escala.

    Entradas en el glosario

    Definición: Escala

    Una escala indica cómo las medidas en un dibujo a escala representan las medidas reales del objeto.

    Por ejemplo, la escala en este plano de planta nos dice que 1 pulgada en el dibujo representa 8 pies en la habitación real. Esto significa que 2 pulgadas representarían 16 pies, y\(\frac{1}{2}\) pulgada representaría 4 pies.

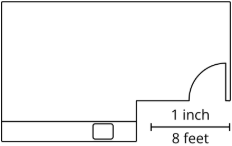
    clipboard_e9867a6d2433db50f97bf23fc8e1eef82.png
    Figura\(\PageIndex{6}\)

    Definición: Dibujo a Escala

    Un dibujo a escala representa un lugar u objeto real. Todas las medidas en el dibujo corresponden a las medidas del objeto real por la misma escala.

    clipboard_e55b83d43294527ca40129e80a7ea2d90.png
    Figura\(\PageIndex{7}\)

    Practica

    Ejercicio\(\PageIndex{4}\)

    Una imagen de un libro que se muestra en un sitio web es de 1.5 pulgadas de ancho y 3 pulgadas de alto en un monitor de computadora. El libro real es de 9 pulgadas de ancho.

    1. ¿Qué escala se está utilizando para la imagen?
    2. ¿Qué tan alto es el libro real?

    Ejercicio\(\PageIndex{5}\)

    La bandera de Colombia es un rectángulo de 6 pies de largo con tres franjas horizontales.

    clipboard_ecbc7dd61dffbf7fa9b30b2e6214d0d9c.png
    Figura\(\PageIndex{8}\): Figura rectangular que representa una bandera. El rectángulo está dividido por dos líneas horizontales. Se dibuja la primera línea horizontal dividiendo el rectángulo por la mitad y la mitad superior está sombreada en amarillo. La segunda línea horizontal se dibuja a medio camino entre la primera línea horizontal y la base del rectángulo. La sección media está sombreada en azul y la sección inferior está sombreada en rojo. Bandera de Colombia, por SkoPP. Dominio Público. Wikimedia Commons. Fuente.
    • La franja superior mide 2 pies de alto y es amarilla.
    • La franja media mide 1 pie de alto y es azul.
    • La franja inferior también mide 1 pie de alto y es roja.
    1. Crear un dibujo a escala de la bandera colombiana con una escala de 1 cm a 2 pies.
    2. Crear un dibujo a escala de la bandera colombiana con una escala de 2 cm a 1 pie.

    Ejercicio\(\PageIndex{6}\)

    Estos triángulos son copias escaladas entre sí.

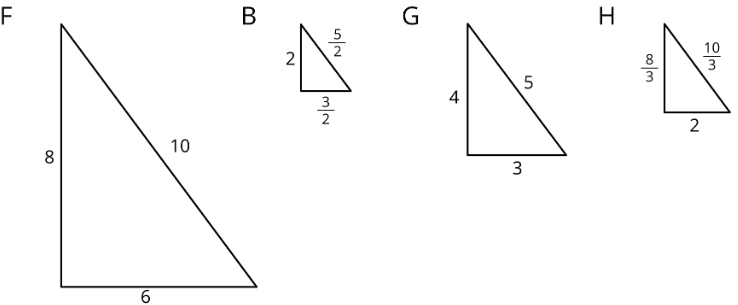
    clipboard_ede465096762d8f6c98b0f828fb494998.png
    Figura\(\PageIndex{9}\): Cuatro triángulos rectos etiquetados con F, B, G y H. El triángulo F tiene el lado vertical etiquetado con 8, el lado horizontal etiquetado con 6 y el lado más largo etiquetado con 10. El triángulo B tiene el lado vertical etiquetado 2, el lado horizontal etiquetado con 3 mitades y el lado más largo etiquetado con 5 mitades. El triángulo G tiene el lado vertical etiquetado como 4, el lado horizontal etiquetado con 3 y el lado más largo etiquetado con 5. El triángulo H tiene el lado vertical etiquetado 8 tercios, el lado horizontal etiquetado 2 y el lado más largo etiquetado 10 tercios.

    Por cada par de triángulos enumerados, el área del segundo triángulo es ¿cuántas veces más grande que el área del primero?

    1. Triángulo G y Triángulo F
    2. Triángulo G y Triángulo B
    3. Triángulo B y Triángulo F
    4. Triángulo F y Triángulo H
    5. Triángulo G y Triángulo H
    6. Triángulo H y Triángulo B

    (De la Unidad 1.1.6)

    Ejercicio\(\PageIndex{7}\)

    Aquí hay un rectángulo sin etiquetar, seguido de otros cuadriláteros que están etiquetados.

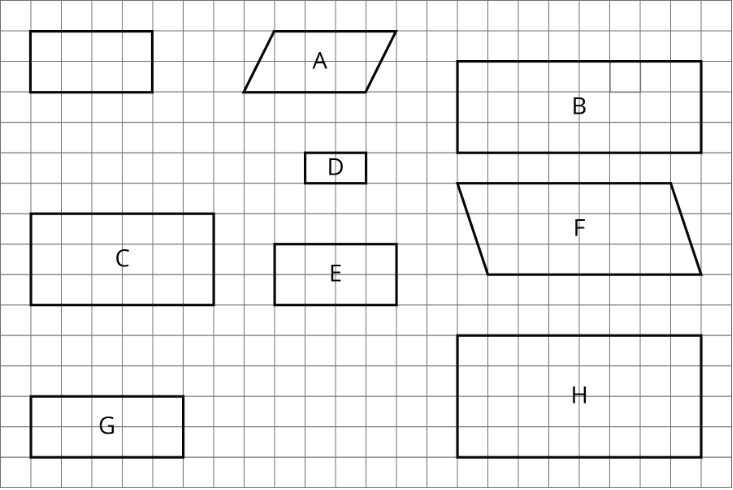
    clipboard_e4f80cf111a81b41d54b87e48f17d0d39.png
    La Figura B tiene longitudes laterales 8, 3, 8, 3. C tiene longitudes laterales 6, 3, 6, 3. D tiene 2, 1, 2, 1. E tiene 4, 2, 4, 2. F tiene 7, lado diagonal hacia abajo 3, derecho 1, 7, y lado diagonal izquierdo 1, arriba 3. G tiene 5, 2, 5, 2. H tiene 8, 4, 8, 4.
    1. Seleccione todos los cuadriláteros que sean copias escaladas del rectángulo sin etiquetar. Explique cómo sabe.
    2. En papel cuadriculado, dibuje una versión a escala diferente del rectángulo original.

    (De la Unidad 1.1.3)

    This page titled 1.2.3: Creación de dibujos a escala is shared under a CC BY license and was authored, remixed, and/or curated by Illustrative Mathematics.