Saltar al contenido principal
LibreTexts Español

1.2.4: Cambio de Escalas en Dibujos a Escala

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    119326

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Lección

    Exploremos diferentes dibujos a escala de la misma cosa real.

    Ejercicio\(\PageIndex{1}\): Appropriate Measurements

    1. Si un estudiante usa una regla como esta para medir la longitud de su pie, ¿qué opciones serían las medidas apropiadas? Seleccione todas las que correspondan. Esté preparado para explicar su razonamiento.

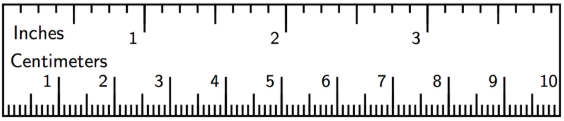
    clipboard_ebfc92499dec620b2ecae0bfb97399a46.png
    Figura\(\PageIndex{1}\)
    1. \(9\frac{1}{4}\)pulgadas
    2. \(9\frac{5}{64}\)pulgadas
    3. \(23.47659\)centímetros
    4. \(23.5\)centímetros
    5. \(23.48\)centímetros

    2. Aquí hay un dibujo a escala del pie promedio de un estudiante de séptimo grado junto a un dibujo a escala de un pie perteneciente a la persona con los pies más grandes del mundo. Estimar la longitud del pie más grande.

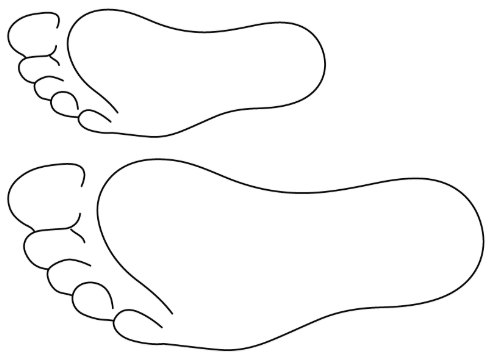
    clipboard_ec797cff5bbf4292f38e7bb6bc53567ff.png
    Figura\(\PageIndex{2}\)

    Ejercicio\(\PageIndex{2}\): Same Plot, Different Drawings

    Aquí hay un mapa que muestra una parcela de tierra en forma de triángulo rectángulo.

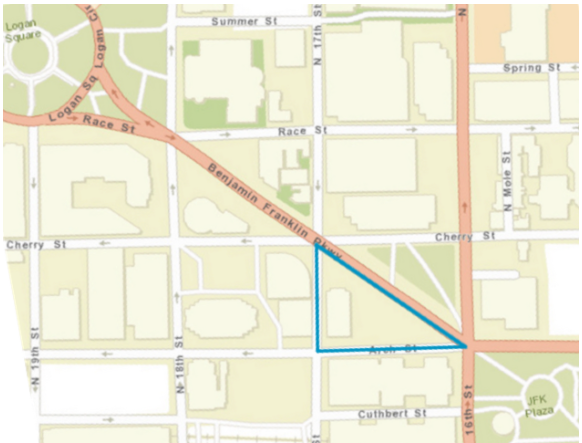
    clipboard_e41ae0d1d939caddcd901a10a32590e18.png
    Figura\(\PageIndex{3}\): Por American Fact Finder. Dominio Público. Buscador de hechos americano. Fuente.
    1. Tu profesor te asignará una báscula para usar. En papel cuadriculado de centímetros, hacer un dibujo a escala de la parcela de tierra. Asegúrate de escribir tu báscula en tu dibujo.
    2. ¿Cuál es el área del triángulo que dibujaste? Explica o muestra tu razonamiento.
    3. ¿Cuántos metros cuadrados están representados por 1 centímetro cuadrado en tu dibujo?
    4. Después de que todos en su grupo hayan terminado, ordene los dibujos a escala de mayor a menor. ¿Qué nota de las básculas cuando sus dibujos se colocan en este orden?

    ¿Estás listo para más?

    Noé y Elena hacen cada uno un dibujo a escala del mismo terreno triangular, utilizando las siguientes escalas. Haz una predicción sobre el tamaño de cada dibujo. ¿Cómo se compararían con los dibujos a escala realizados por su grupo?

    1. Noé utiliza la escala de 1 cm a 200 m.
    2. Elena utiliza la escala de 2 cm a 25 m.

    Ejercicio\(\PageIndex{3}\): A New Drawing of the Playground

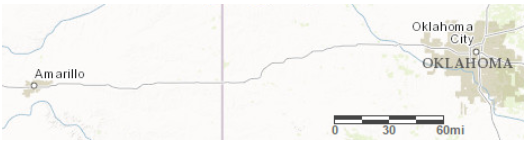
    Aquí hay un dibujo a escala de un patio de recreo.

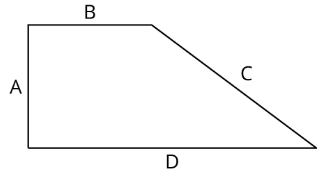
    clipboard_ef676648fbc42c01d4fc26daf8819f327.png
    Figura\(\PageIndex{4}\)

    La escala es de 1 centímetro a 30 metros.

    1. Hacer otro dibujo a escala del mismo patio de recreo a una escala de 1 centímetro a 20 metros.
    2. ¿Cómo se comparan los dos dibujos a escala?

    Resumen

    A veces tenemos un dibujo a escala de algo, y queremos crear otro dibujo a escala del mismo que utilice una escala diferente. Podemos usar el dibujo a escala original para encontrar el tamaño del objeto real. Entonces podemos usar el tamaño del objeto real para averiguar el tamaño de nuestro nuevo dibujo a escala.

    Por ejemplo, aquí hay un dibujo a escala de un parque donde la escala es de 1 cm a 90 m.

    clipboard_e0a7da4e1b50dfbbc4398a76f7fc99bd8.png
    Figura\(\PageIndex{5}\)

    El rectángulo es de 10 cm por 4 cm, por lo que las dimensiones reales del parque son 900 m por 360 m, porque\(10\cdot 90=900\) y\(4\cdot 90=360\).

    Supongamos que queremos hacer otro dibujo a escala del parque donde la escala es de 1 cm a 30 metros. Este nuevo dibujo a escala debe ser de 30 cm por 12 cm, porque\(900\div 30=30\) y\(360\div 30=12\).

    Otra forma de encontrar esta respuesta es pensar en cómo las dos escalas diferentes se relacionan entre sí. En el primer dibujo a escala, 1 cm representaba 90 m. En el nuevo dibujo, necesitaríamos 3 cm para representar 90 m. Esto significa que cada longitud en el nuevo dibujo a escala debe ser 3 veces mayor que en el dibujo original. El nuevo dibujo a escala debe ser de 30 cm por 12 cm, porque\(3\cdot 10=30\) y\(3\cdot 4=12\).

    Dado que el largo y ancho son 3 veces más largos, el área del nuevo dibujo a escala será 9 veces más grande que el área del dibujo a escala original, porque\(3^{2}=9\).

    Entradas en el glosario

    Definición: Escala

    Una escala indica cómo las medidas en un dibujo a escala representan las medidas reales del objeto.

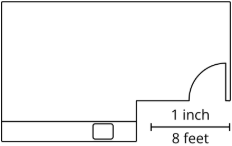
    Por ejemplo, la escala en este plano de planta nos dice que 1 pulgada en el dibujo representa 8 pies en la habitación real. Esto significa que 2 pulgadas representarían 16 pies, y\(\frac{1}{2}\) pulgada representaría 4 pies.

    clipboard_e9867a6d2433db50f97bf23fc8e1eef82.png
    Figura\(\PageIndex{6}\)

    Definición: Dibujo a Escala

    Un dibujo a escala representa un lugar u objeto real. Todas las medidas en el dibujo corresponden a las medidas del objeto real por la misma escala.

    clipboard_e55b83d43294527ca40129e80a7ea2d90.png
    Figura\(\PageIndex{7}\)

    Practica

    Ejercicio\(\PageIndex{4}\)

    Aquí hay un dibujo a escala de una piscina donde 1 cm representa 1 m.

    clipboard_e970ae6605f9b193597646e432c572849.png
    Figura\(\PageIndex{8}\)
    1. ¿Cuánto tiempo y qué tan amplia es la piscina real?
    2. ¿Un dibujo a escala donde 1 cm representa 2 m será mayor o menor que este dibujo?
    3. Hacer un dibujo a escala de la piscina donde 1 cm representa 2 m.

    Ejercicio\(\PageIndex{5}\)

    Un mapa de un parque tiene una escala de 1 pulgada a 1,000 pies. Otro mapa del mismo parque tiene una escala de 1 pulgada a 500 pies. ¿Qué mapa es más grande? Explica o muestra tu razonamiento.

    Ejercicio\(\PageIndex{6}\)

    En un mapa con una escala de 1 pulgada a 12 pies, el área de un restaurante es de 60 en 2. Han dice que el área real del restaurante es de 720 pies 2. ¿Estás de acuerdo o en desacuerdo? Explica tu razonamiento.

    Ejercicio\(\PageIndex{7}\)

    Si Cuadrilátero Q es una copia a escala de Cuadrilátero P creada con un factor de escala de 3, ¿cuál es el perímetro de Q?

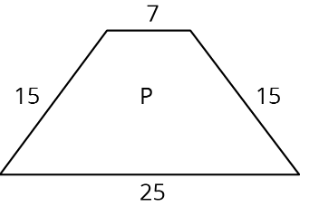
    clipboard_ea6feb82c4804d654d5f3e36aa49f3043.png
    Figura\(\PageIndex{9}\): Un trapecio etiquetado P. Los lados paralelos forman la parte superior e inferior de la forma. La longitud del lado superior está etiquetada con 7 unidades y la longitud del lado inferior está etiquetada con 25 unidades. Las dos patas que unen los dos lados paralelos están etiquetadas cada una con 15 unidades.

    (De la Unidad 1.1.3)

    Ejercicio\(\PageIndex{8}\)

    Triángulo\(DEF\) es una copia a escala del triángulo\(ABC\). Para cada una de las siguientes partes del triángulo\(ABC\), identifique la parte correspondiente del triángulo\(DEF\).

    • ángulo\(ABC\)
    • ángulo\(BCA\)
    • segmento\(AC\)
    • segmento\(BA\)
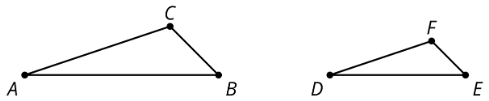
    clipboard_e64afd8db72a21fbea65a7ee4691206f4.png
    Figura\(\PageIndex{10}\): Dos triángulos etiquetados ABC y DEF. El triángulo ABC tiene el lado horizontal AB con el punto B a la derecha del punto A y el punto C está directamente encima del lado AB. El triángulo DEF tiene el lado horizontal DE con el punto E a la derecha del punto D y el punto F está directamente encima del lado DE.

    (De la Unidad 1.1.2)

    This page titled 1.2.4: Cambio de Escalas en Dibujos a Escala is shared under a CC BY license and was authored, remixed, and/or curated by Illustrative Mathematics.