2.1.2: Introducción de relaciones proporcionales con tablas

Última actualización
Guardar como PDF

Page ID: 119167

Illustrative Mathematics
OpenUp Resources

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Lección

Resolvamos problemas que involucran relaciones proporcionales usando tablas.

Ejercicio\(\PageIndex{1}\): NOtice and Wonder: Paper Towels by The Case

Aquí hay una tabla que muestra cuántos rollos de toallas de papel recibe una tienda cuando piden diferentes números de estuches.

Figura\(\PageIndex{1}\): Tabla con 2 columnas y 4 filas de datos. Las columnas son: número de cajas que ordenan y número de rollos de toallas de papel. La tabla tiene los pares ordenados (1 coma 12), (2 coma 36), (5 coma 60) y (10 coma 120). Hay una flecha apuntando de la fila 3 a la fila 4 en cada lado con tiempos 2 junto a las flechas.

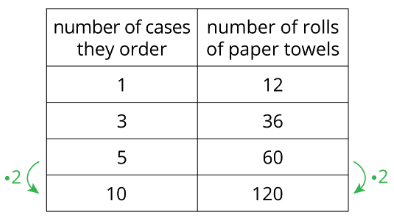
¿Qué notas de la mesa? ¿Qué te preguntas?

Ejercicio\(\PageIndex{2}\): Feeding a Crowd

Una receta dice que 2 tazas de arroz seco servirán a 6 personas. Completa la tabla mientras respondes las preguntas. Esté preparado para explicar su razonamiento.

¿Cuántas personas servirán 10 tazas de arroz?

¿Cuántas tazas de arroz se necesitan para servir a 45 personas?

Mesa\(\PageIndex{1}\)
tazas de arroz	número de personas
2	6
3	9
10
	45

Una receta dice que 6 rollitos de primavera servirán a 3 personas. Completa la tabla.

Mesa\(\PageIndex{2}\)
número de rollitos de primavera	número de personas
6	3
30
40
	28

Ejercicio\(\PageIndex{3}\): Making Bread Dough

Una panadería utiliza 8 cucharadas de miel por cada 10 tazas de harina para hacer masa de pan. Algunos días hornean lotes más grandes y algunos días hornean lotes más pequeños, pero siempre usan la misma proporción de miel a harina. Completa la tabla mientras respondes las preguntas. Esté preparado para explicar su razonamiento.

¿Cuántas tazas de harina usan con 20 cucharadas de miel?
¿Cuántas tazas de harina usan con 13 cucharadas de miel?
¿Cuántas cucharadas de miel usan con 20 tazas de harina?
¿Cuál es la relación proporcional que representa esta tabla?

Mesa\(\PageIndex{3}\)
miel (cda)	harina (c)
8	10
20
13
	20

Ejercicio\(\PageIndex{4}\): Quarters and Dimes

4 trimestres son iguales en valor a 10 dimes.

¿Cuántas dimes es igual al valor de 6 trimestres?
¿Cuántas dimes es igual al valor de 14 trimestres?
¿Qué valor pertenece al lado del 1 en la tabla? ¿Qué significa en este contexto?

Mesa\(\PageIndex{4}\)
número de cuartos	número de dimes
1
4	20
6
14

¿Estás listo para más?

Los centavos hechos antes de 1982 son 95% de cobre y pesan alrededor de 3.11 gramos cada uno. (Los centavos hechos después de esa fecha están hechos principalmente de zinc). Algunas personas afirman que el valor del cobre en uno de estos centavos es mayor que el valor nominal del centavo. Entérate de cuánto vale el cobre en este momento, y decide si esta afirmación es cierta.

Resumen

Si las relaciones entre dos cantidades correspondientes son siempre equivalentes, la relación entre las cantidades se denomina relación proporcional.

Esta tabla muestra diferentes cantidades de leche y jarabe de chocolate. Los ingredientes de cada fila, cuando se mezclan juntos, harían una cantidad total diferente de leche de chocolate, pero todas estas mezclas sabrían igual.

Mesa\(\PageIndex{5}\)
cucharadas de sirope de chocolate	tazas de leche
\(4\)	\(1\)
\(6\)	\(1\frac{1}{2}\)
\(8\)	\(2\)
\(\frac{1}{2}\)	\(\frac{1}{8}\)
\(12\)	\(3\)
\(1\)	\(\frac{1}{4}\)

Observe que cada fila de la tabla muestra una proporción de cucharadas de jarabe de chocolate a tazas de leche que es equivalente a\(4:1\).

Sobre la relación entre estas cantidades, podríamos decir:

La relación entre la cantidad de jarabe de chocolate y la cantidad de leche es proporcional.
La relación entre la cantidad de jarabe de chocolate y la cantidad de leche es una relación proporcional.
El cuadro representa una relación proporcional entre la cantidad de jarabe de chocolate y la cantidad de leche.
La cantidad de leche es proporcional a la cantidad de jarabe de chocolate.

Podríamos multiplicar cualquier valor en la columna de jarabe de chocolate por\(\frac{1}{4}\) para obtener el valor en la columna de leche. Podríamos llamar a\(\frac{1}{4}\) una tarifa unitaria, porque se necesitan\(\frac{1}{4}\) tazas de leche para 1 cucharada de sirope de chocolate. También decimos que\(\frac{1}{4}\) es la constante de proporcionalidad para esta relación. Nos dice cuántas tazas de leche necesitaríamos mezclar con 1 cucharada de sirope de chocolate.

Entradas en el glosario

Definición: Constante de proporcionalidad

En una relación proporcional, los valores de una cantidad se multiplican cada uno por el mismo número para obtener los valores de la otra cantidad. A este número se le llama la constante de proporcionalidad.

En este ejemplo, la constante de proporcionalidad es 3, porque\(2\cdot 3=6\),\(3\cdot 3=9\), y\(5\cdot 3=15\). Esto significa que hay 3 manzanas por cada 1 naranja en la ensalada de frutas.

Mesa\(\PageIndex{6}\)
número de naranjas	número de manzanas
2	6
3	9
5	15

Definición: Relaciones Equivalentes

Dos ratios son equivalentes si puedes multiplicar cada uno de los números en la primera relación por el mismo factor para obtener los números en la segunda proporción. Por ejemplo,\(8:6\) es equivalente a\(4:3\), porque\(8\cdot\frac{1}{2}=4\) y\(6\cdot\frac{1}{2}=3\).

Una receta de limonada dice usar 8 tazas de agua y 6 limones. Si usamos 4 tazas de agua y 3 limones, hará la mitad de limonada. Ambas recetas saben igual, porque y son proporciones equivalentes.

Mesa\(\PageIndex{7}\)
tazas de agua	número de limones
8	6
4	3

Definición: Relación proporcional

En una relación proporcional, los valores de una cantidad se multiplican cada uno por el mismo número para obtener los valores de la otra cantidad.

Por ejemplo, en esta tabla cada valor de\(p\) es igual a 4 veces el valor de\(s\) en la misma fila.

Podemos escribir esta relación como\(p=4s\). Esta ecuación muestra que\(s\) es proporcional a\(p\).

Mesa\(\PageIndex{8}\)
\(s\)	\(p\)
\ (s\) ">2	\ (p\) ">8
\ (s\) ">3	\ (p\) ">12
\ (s\) ">5	\ (p\) ">20
\ (s\) ">10	\ (p\) ">40

Practica

Ejercicio\(\PageIndex{5}\)

Cuando Han hace leche de chocolate, mezcla 2 tazas de leche con 3 cucharadas de sirope de chocolate. Aquí hay una tabla que muestra cómo hacer lotes de diferentes tamaños. Utilice la información de la tabla para completar las declaraciones. Algunos términos se utilizan más de una vez.

Figura\(\PageIndex{2}\): Tabla con 2 columnas y 4 filas de datos. Las columnas son: tazas de leche y cucharadas de sirope de chocolate. La tabla tiene los pares ordenados (2 coma 3), (8 coma 12), (1 coma la fracción 3 sobre 2) y (10 coma 15). Hay una flecha apuntando de la fila 1 a la fila 2 en cada lado con tiempos 4 junto a las flechas.

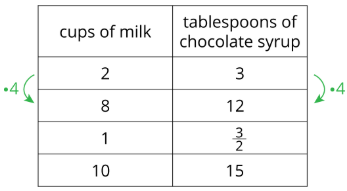
El cuadro muestra una relación proporcional entre ______________ y ______________.
El factor de escala que se muestra es ______________.
La constante de proporcionalidad para esta relación es______________.
Las unidades para la constante de proporcionalidad son ______________ por ______________.

Banco de Términos: cucharadas de sirope de chocolate, 4, tazas de leche, taza de leche,\(\frac{3}{2}\)

Ejercicio\(\PageIndex{6}\)

Un cierto tono de rosa se crea agregando 3 tazas de pintura roja a 7 tazas de pintura blanca.

¿Cuántas tazas de pintura roja se deben agregar a 1 taza de pintura blanca?

Mesa\(\PageIndex{9}\)
tazas de pintura blanca	tazas de pintura roja
1
7	3

¿Cuál es la constante de proporcionalidad?

Ejercicio\(\PageIndex{7}\)

Un mapa de un parque rectangular tiene una longitud de 4 pulgadas y un ancho de 6 pulgadas. Utiliza una escala de 1 pulgada por cada 30 millas.

¿Cuál es el área real del parque? Muestra cómo sabes.
El mapa necesita ser reproducido a una escala diferente para que tenga un área de 6 pulgadas cuadradas y pueda caber en un folleto. ¿A qué escala se debe reproducir el mapa para que encaje en el folleto? Muestra tu razonamiento.

(De la Unidad 1.2.6)

Ejercicio\(\PageIndex{8}\)

Noé dibujó una copia a escala del Polígono P y lo etiquetó Polígono Q.

Figura\(\PageIndex{3}\): Polígono Q en una cuadrícula. El polígono Q tiene 8 lados. Comenzando en la esquina inferior izquierda, el primer lado está 9 unidades hacia arriba, el segundo lado es 6 unidades a la derecha, el tercer lado está 3 unidades hacia abajo, el cuarto lado está 3 unidades a la izquierda, el quinto lado es 3 unidades hacia abajo, el sexto lado es 3 unidades a la derecha, el séptimo lado es 3 unidades hacia abajo, y el octavo lado queda 6 unidades.

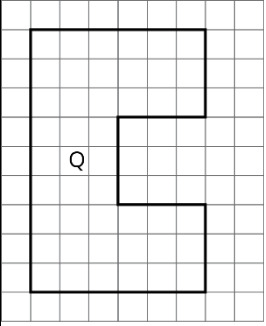
Si el área del Polígono P es de 5 unidades cuadradas, ¿qué factor de escala aplicó Noé al Polígono P para crear Polígono Q? Explique o muestre cómo sabe.

(De la Unidad 1.1.6)

Ejercicio\(\PageIndex{9}\)

Seleccione todas las proporciones que sean equivalentes entre sí.

\(4:7\)
\(8:15\)
\(16:28\)
\(2:3\)
\(20:35\)