6.1.3: Razonamiento sobre ecuaciones con diagramas de cinta

Lección

Veamos cómo las ecuaciones pueden describir los diagramas de cinta.

Ejercicio\(\PageIndex{1}\): Find Equivalent Expressions

Seleccione todas las expresiones que sean equivalentes a\(7(2-3n)\). Explica cómo sabes que cada expresión que selecciones es equivalente.

1. \(9-10n\)
2. \(14-3n\)
3. \(14-21n\)
4. \((2-3n)\cdot 7\)
5. \(7\cdot 2\cdot (-3n)\)

Ejercicio\(\PageIndex{2}\): Matching Equations to Tape Diagrams

Figura\(\PageIndex{1}\)

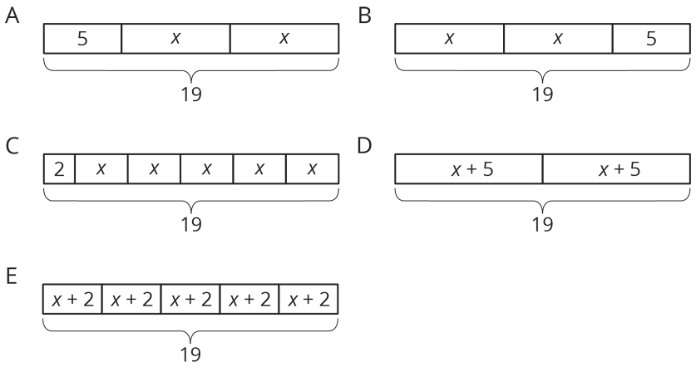
1. Haga coincidir cada ecuación con uno de los diagramas de cinta. Esté preparado para explicar cómo la ecuación coincide con el diagrama.
2. Ordena las ecuaciones en categorías de tu elección. Explicar los criterios para cada categoría.

• \(2x+5=19\)
• \(2+5x=19\)
• \(2(x+5)=19\)
• \(5(x+2)=19\)
• \(19=5+2x\)
• \((x+5)\cdot 2=19\)
• \(19=(x+2)\cdot 5\)
• \(19\div 2=x+5\)
• \(19-2=5x\)

Ejercicio\(\PageIndex{3}\): Drawing Tape Diagrams to Represent Equations

1. Dibuja un diagrama de cinta para que coincida con cada ecuación.
   1. \(114=3x+18\)
   2. \(114=3(y+18)\)
2. Usa cualquier método para encontrar valores para\(x\) y\(y\) que hagan verdaderas las ecuaciones.

¿Estás listo para más?

Para hacer un copo de nieve de Koch:

• Comienza con un triángulo equilátero que tenga longitudes laterales de 1. Este es el paso 1.
• Reemplazar el tercio medio de cada segmento de línea con un pequeño triángulo equilátero con el tercio medio del segmento formando la base. Este es el paso 2.
• Haga lo mismo con cada uno de los segmentos de línea. Este es el paso 3.
• Sigue repitiendo este proceso.

Figura\(\PageIndex{2}\): Tres figuras. Primero, un triángulo equilátero. Segundo, el mismo triángulo equilátero, pero cada borde lateral se divide en tercios y el tercio medio forma la base de un triángulo equilátero. Tercero, la segunda imagen, pero cada borde lateral se divide en tercios y el tercio medio forma la base de un triángulo equilátero.

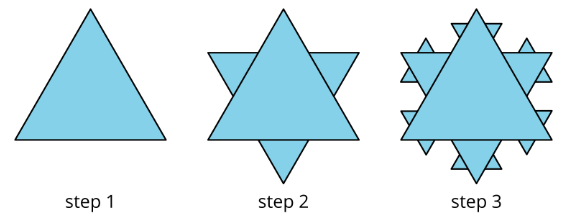
1. ¿Cuál es el perímetro después del paso 2? ¿Paso 3?
2. ¿Qué sucede con el perímetro, o la longitud de la línea trazada a lo largo del exterior de la figura, a medida que continúa el proceso?

Resumen

Hemos visto cómo los diagramas de cinta representan las relaciones entre cantidades. Debido al significado y las propiedades de la suma y la multiplicación, a menudo se puede usar más de una ecuación para representar un solo diagrama de cinta.

Echemos un vistazo a dos diagramas de cinta.

Figura\(\PageIndex{3}\)

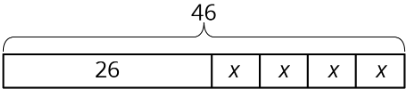
Podemos describir este diagrama con varias ecuaciones diferentes. Éstos son algunos de ellos:

• \(26+4x=46\), porque las partes se suman al conjunto.
• \(4x+26=46\), porque la adición es conmutativa.
• \(46=4x+26\), porque si dos cantidades son iguales, no importa cómo las arreglemos alrededor del signo igual.
• \(4x=46-26\), porque una parte (la parte conformada por\(4x\)'s) es la diferencia entre el todo y la otra parte.

Figura\(\PageIndex{4}\)

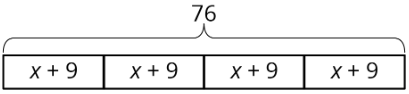
Para este diagrama:

• \(4(x+9)=76\), porque multiplicar significa tener múltiples grupos del mismo tamaño.
• \((x+9) \cdot 4=76\), porque la multiplicación es conmutativa.
• \(76\div 4=x+9\), porque la división nos dice el tamaño de cada parte igual.

Entradas en el glosario

Definición: Expresiones equivalentes

Las expresiones equivalentes son siempre iguales entre sí. Si las expresiones tienen variables, son iguales siempre que se use el mismo valor para la variable en cada expresión.

Por ejemplo,\(3x+4x\) es equivalente a\(5x+2x\). No importa para qué valor usemos\(x\), estas expresiones son siempre iguales. Cuando\(x\) es 3, ambas expresiones equivalen a 21. Cuando\(x\) es 10, ambas expresiones equivalen a 70.

Practica

Ejercicio\(\PageIndex{4}\)

Resuelve cada ecuación mentalmente.

1. \(2x=10\)
2. \(-3x=21\)
3. \(\frac{1}{3}x=6\)
4. \(-\frac{1}{2}x=-7\)

(De la Unidad 5.5.1)

Ejercicio\(\PageIndex{5}\)

Completa los cuadrados mágicos para que la suma de cada fila, cada columna y cada diagonal en una cuadrícula sean todas iguales.

Figura\(\PageIndex{5}\): Tres cuadrículas cuadradas, cada una con 3 columnas y 3 filas. La primera cuadrícula contiene 0, 7, 2, en blanco, 3, en blanco, en blanco, en blanco, en blanco. La segunda cuadrícula contiene 1, en blanco, en blanco, en blanco, 3, negativo 2, en blanco, en blanco, cinco. La tercera cuadrícula contiene blanco, blanco, blanco, 4, 2, 0, negativo 1, blanco, blanco.

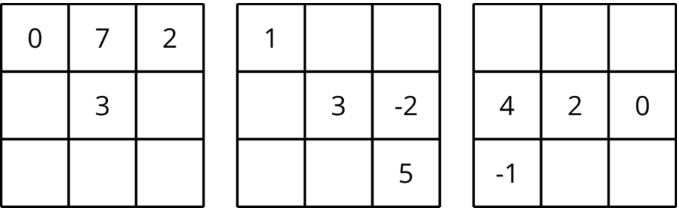
(De la Unidad 5.2.2)

Ejercicio\(\PageIndex{6}\)

Dibuja un diagrama de cinta para que coincida con cada ecuación.

1. \(5(x+1)=20\)
2. \(5x+1=20\)

Ejercicio\(\PageIndex{7}\)

Seleccione todas las ecuaciones que coincidan con el diagrama de cinta.

Figura\(\PageIndex{6}\)

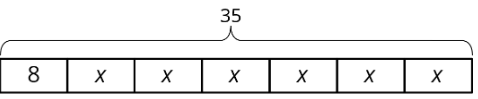
1. \(35=8+x+x+x+x+x+x\)
2. \(35=8+6x\)
3. \(6+8x=35\)
4. \(6x+8=35\)
5. \(6x+8x=35x\)
6. \(35-8=6x\)

Ejercicio\(\PageIndex{8}\)

Cada automóvil viaja a una velocidad constante. Encuentra el número de millas que recorre cada auto en 1 hora a la tarifa indicada.

1. \(135\)millas en\(3\) horas
2. \(22\)millas en\(\frac{1}{2}\) hora
3. \(7.5\)millas en\(\frac{1}{4}\) hora
4. \(\frac{100}{3}\)millas en\(\frac{2}{3}\) hora
5. \(97\frac{1}{2}\)millas en\(\frac{3}{2}\) hora

(De la Unidad 4.1.2)