6.1.4: Razonamiento sobre ecuaciones y diagramas de cinta (Parte 1)

Última actualización
Guardar como PDF

Page ID: 119057

Illustrative Mathematics
OpenUp Resources

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Lección

Veamos cómo los diagramas de cinta pueden ayudarnos a responder preguntas sobre cantidades desconocidas en historias.

Ejercicio$\PageIndex{1}$: Algebra Talk: Seeing Structure

Encuentra una solución a cada ecuación sin anotar nada.

$x+1=5$

$2(x+1)=10$

$3(x+1)=15$

$500=100(x+1)$

Ejercicio$\PageIndex{2}$: Situations and Diagrams

Dibuja un diagrama de cinta para representar cada situación. Para algunas de las situaciones, es necesario decidir qué representar con una variable.

Diego tiene 7 paquetes de marcadores. Cada paquete tiene$x$ marcadores en él. Después de que Lin le da 9 marcadores más, tiene un total de 30 marcadores.
Elena está cortando una cinta de 30 pies para un proyecto artesanal. Ella corta 7 pies, y luego corta la pieza restante en 9 longitudes iguales de$x$ pies cada una.
Un gerente de construcción pesa un paquete de 9 ladrillos idénticos y un bloque de concreto de 7 libras. El paquete pesa 30 libras.
Una pista de patinaje cobra una tarifa grupal de $9 más una tarifa para alquilar cada par de patines. Una familia alquila 7 pares de patines y paga un total de $30.
Andre horna 9 sartenes de brownies. Dona 7 sartenes a la venta de repostería escolar y se queda con el resto para dividir por igual entre su clase de 30 alumnos.

Ejercicio$\PageIndex{3}$: Situations, Diagrams, and Equations

Cada situación en la actividad anterior está representada por una de las ecuaciones.

$7x+9=30$
$30=9x+7$
$30x+7=9$

Coincidir cada situación con una ecuación.
Encuentra la solución a cada ecuación. Usa tus diagramas para ayudarte a razonar.
¿Qué te dice cada solución sobre su situación?

¿Estás listo para más?

Mientras esté en la ciudad de Nueva York, ¿es mejor que un grupo de amigos tome un taxi o el metro para llegar del Empire State Building al Metropolitan Museum of Art? Explica tu razonamiento.

Resumen

Muchas situaciones pueden ser representadas por ecuaciones. Escribir una ecuación para representar una situación puede ayudarnos a expresar cómo las cantidades en la situación se relacionan entre sí, y puede ayudarnos a razonar sobre cantidades desconocidas cuyo valor queremos saber. Aquí hay tres situaciones:

Un arquitecto está redactando planos para un nuevo supermercado. Habrá un espacio de 144 pulgadas de largo para filas de carritos de compras anidados. El primer carrito mide 34 pulgadas de largo y cada carrito anidado agrega otras 10 pulgadas. El arquitecto quiere saber cuántos carritos de compras cabrán en cada fila.
Una panadería compra una bolsa grande de azúcar que tiene 34 tazas. Usan 10 tazas para hacer algunas galletas. Después usan el resto de la bolsa para hacer 144 magdalenas gigantes. Sus clientes quieren saber cuánta azúcar hay en cada muffin.
Kiran está tratando de ahorrar 144 dólares para comprar una guitarra nueva. Tiene 34 dólares y va a ahorrar 10 dólares a la semana del dinero que gana cortando el césped. Quiere saber cuántas semanas le llevará tener suficiente dinero para comprar la guitarra.

Vemos los mismos tres números en las situaciones: 10, 34 y 144. ¿Cómo podríamos representar cada situación con una ecuación?

En la primera situación, hay un carrito de compras con longitud 34 y luego un número desconocido de carritos con longitud 10. De igual manera, Kiran tiene 34 dólares ahorrados y luego ahorrará 10 cada semana por un número desconocido de semanas. Ambas situaciones tienen una parte de 34 y luego partes iguales de tamaño 10 que suman todas juntas a 144. Su ecuación es$34+10x=144$.

Ya que se necesitan 11 grupos de 10 para llegar de 34 a 144, el valor de$x$ en estas dos situaciones es$(144-34)\div 10$ o 11. Habrá 11 carritos de compras en cada fila, y Kiran tardará 11 semanas en recaudar el dinero para la guitarra.

En la situación de panadería, hay una parte de 10 y luego 144 partes iguales de tamaño desconocido que suman todas juntas a 34. La ecuación es$10+144x=34$. Ya que se necesita 24 para obtener de 10 a 34, el valor de$x$ es$(34-10)\div 144$ o$\frac{1}{6}$. Hay$\frac{1}{6}$ taza de azúcar en cada muffin gigante.

Entradas en el glosario

Definición: Expresiones equivalentes

Las expresiones equivalentes son siempre iguales entre sí. Si las expresiones tienen variables, son iguales siempre que se use el mismo valor para la variable en cada expresión.

Por ejemplo,$3x+4x$ es equivalente a$5x+2x$. No importa para qué valor usemos$x$, estas expresiones son siempre iguales. Cuando$x$ es 3, ambas expresiones equivalen a 21. Cuando$x$ es 10, ambas expresiones equivalen a 70.

Practica

Ejercicio$\PageIndex{4}$

Dibuja un cuadrado con longitud lateral de 7 cm.

Predecir el perímetro y la longitud de la diagonal del cuadrado.
Mida el perímetro y la longitud de la diagonal del cuadrado.
Describir qué tan cerca están las predicciones y mediciones.

(De la Unidad 3.1.1)

Ejercicio$\PageIndex{5}$

Encuentra los productos.

$(100)\cdot (-0.09)$
$(-7)\cdot (-1.1)$
$(-7.3)\cdot (5)$
$(-0.2)\cdot (-0.3)$

(De la Unidad 5.3.2)

Ejercicio$\PageIndex{6}$

Aquí hay tres historias:

Una familia compra 6 boletos para un espectáculo. También pagan una cuota de estacionamiento de $3. Gastan 27 dólares para ver el espectáculo.
Diego tiene 27 onzas de jugo. Él vierte cantidades iguales por cada uno de sus 3 amigos y le quedan 6 onzas para sí mismo.
Jada trabaja durante 6 horas preparándose para la feria de arte. Ella pasa 3 horas en una escultura y luego pinta 27 marcos para cuadros.

Aquí hay tres ecuaciones.

$3x+6=27$
$6x+3=27$
$27x+3=6$

Decide qué ecuación representa cada historia. ¿Qué$x$ representa en cada ecuación?
Encuentra la solución a cada ecuación. Explica o muestra tu razonamiento.
¿Qué te dice cada solución sobre su situación?

Ejercicio$\PageIndex{7}$

Aquí hay un diagrama y su ecuación correspondiente. Encuentra la solución a la ecuación y explica tu razonamiento.

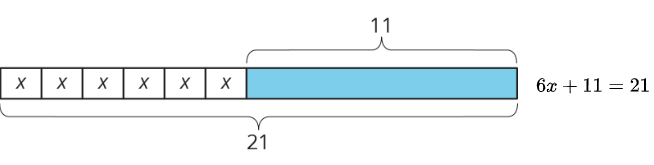
Ejercicio$\PageIndex{8}$

1. Trazar estos puntos en el plano de coordenadas:

$A=(3,2),\: B=(7.5,2),\: C=(7.5, -2.5),\: D=(3,-2)$

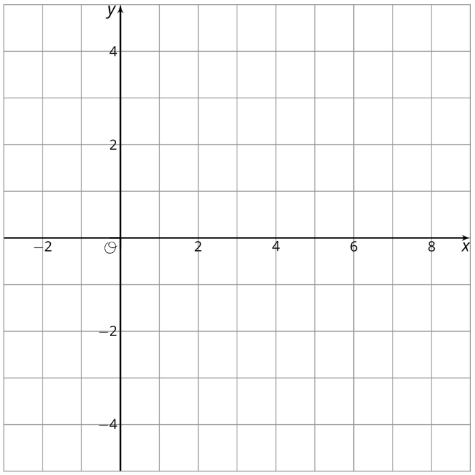
2. ¿Cuál es la diferencia vertical entre$D$ y$A$?

3. Escribe una expresión que represente la distancia vertical entre$B$ y$C$?

(De la Unidad 5.2.6)