6.3.2: Encontrar soluciones a las desigualdades en contexto

Última actualización
Guardar como PDF

Page ID: 119011

Illustrative Mathematics
OpenUp Resources

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Lección

Resolvamos desigualdades más complicadas.

Ejercicio$\PageIndex{1}$: Solutions to Equations and Solutions to Inequalities

Resolver$-x=10$
Encuentra 2 soluciones para$-x>10$
Resolver$2x=-20$
Encuentra 2 soluciones para$2x>-20$

Ejercicio$\PageIndex{2}$: Earning Money For Soccer Stuff

Andre tiene un trabajo de verano vendiendo suscripciones a revistas. Gana 25 dólares por semana más $3 por cada suscripción que vende. Andre espera ganar al menos el dinero suficiente esta semana para comprar un nuevo par de tacos de fútbol.
1. Vamos a$n$ representar el número de suscripciones a revistas que Andre vende esta semana. Escribe una expresión por la cantidad de dinero que gana esta semana.
2. El par de tacos menos caros que Andre quiere cuesta 68 dólares. Escribe y resuelve una ecuación para saber cuántas suscripciones a revistas Andre necesita vender para comprar los tacos.
3. Si Andre vendiera 16 suscripciones a revistas esta semana, ¿alcanzaría su objetivo? Explica tu razonamiento.
4. ¿Cuáles son algunos otros números de suscripciones a revistas que Andre podría haber vendido y aún así alcanzó su meta?
5. Escribe una desigualdad expresando que Andre quiere ganar al menos 68 dólares.
6. Escribe una desigualdad para describir el número de suscripciones que Andre debe vender para alcanzar su objetivo.
Diego ha presupuestado 35 dólares de sus ganancias laborales de verano para comprar pantalones cortos y calcetines para el fútbol. Necesita 5 pares de calcetines y un par de pantalones cortos. Los calcetines cuestan diferentes cantidades en diferentes tiendas. Los pantalones cortos que quiere cuestan $19.95.
1. Vamos a$x$ representar el precio de un par de calcetines. Escribe una expresión para el costo total de los calcetines y pantalones cortos.
2. Escribe y resuelve una ecuación que diga que Diego gastó exactamente 35 dólares en los calcetines y pantalones cortos.
3. Enumere algunos otros posibles precios para los calcetines que aún permitirían que Diego se mantuviera dentro de su presupuesto.
4. Escribe una desigualdad para representar la cantidad que Diego puede gastar en un solo par de calcetines.

Ejercicio$\PageIndex{3}$: Granola Bars and Savings

Kiran tiene $100 guardados en una cuenta bancaria. (La cuenta no gana intereses.) Le pidió a Clare que le ayudara a averiguar cuánto podría sacar cada mes si necesita tener al menos 25 dólares en la cuenta dentro de un año.
1. Clare escribió la desigualdad$-12x+100\geq 25$, donde$x$ representa la cantidad que Kiran saca cada mes. ¿Qué$-12x$ representa?
2. Encuentra algunos valores de$x$ eso funcionaría para Kiran.
3. Podríamos expresar todos los valores que funcionarían usando cualquiera$x\leq\underline{\quad}$ o$x\geq\underline{\quad}$. ¿Cuál debemos usar?
4. Escribe la respuesta a la pregunta de Kiran usando notación matemática.
Un maestro quiere comprar 9 cajas de barras de granola para un viaje escolar. Cada caja suele costar $7, pero muchas tiendas de abarrotes están teniendo una venta en barras de granola esta semana. Diferentes tiendas están vendiendo cajas de barras de granola con diferentes descuentos.
1. Si$x$ representa el monto en dólares del descuento, entonces se puede expresar como el monto que pagará el maestro$9(7-x)$. En esta expresión, ¿qué$7-x$ representa la cantidad?
2. El maestro tiene 36 dólares para gastar en las barras de granola. La ecuación$9(7-x)=36$ representa una situación en la que gasta todos los 36 dólares. Resuelve esta ecuación.
3. ¿Qué significa la solución en esta situación?
4. El profesor no tiene que gastar todos los 36 dólares. Escribir una desigualdad relacionando 36 y$9(7-x)$ representando esta situación.
5. La solución a esta desigualdad debe verse o bien parecida$x\geq 3$ o$x\leq 3$. ¿Cuál crees que es? Explica tu razonamiento.

¿Estás listo para más?

Jada y Diego hornearon un lote grande de galletas.

Seleccionaron$\frac{1}{4}$ de las cookies para dar a sus profesores.
A continuación, tiraron una galleta quemada.
Entregaron$\frac{2}{5}$ las galletas restantes a un hogar de ancianos local.
A continuación, le dieron 3 galletas a algunos niños del barrio.
Envolvían$\frac{2}{3}$ las galletas restantes para guardar para sus amigos.

Después de todo esto, les quedaban 15 galletas. ¿Cuántas galletas hornearon?

Resumen

Supongamos que Elena tiene $5 y vende bolígrafos por $1.50 cada una. Su objetivo es ahorrar 20 dólares. Podríamos resolver la ecuación$1.5x+5=20$ para encontrar el número de bolígrafos$x$,, que Elena necesita vender para poder ahorrar exactamente 20 dólares. Sumar -5 a ambos lados de la ecuación nos da$1.5x=15$, y luego dividir ambos lados por$1.5$ da las$x=10$ plumas de solución.

¿Y si Elena quiere que le sobra algo de dinero? La desigualdad nos$1.5x+5>20$ dice que la cantidad de dinero que gana Elena tiene que ser mayor a 20 dólares. La solución a la ecuación anterior nos ayudará a entender cuáles serán las soluciones a la desigualdad. Sabemos que si vende 10 bolígrafos, ganará $20. Dado que cada bolígrafo le da más dinero, necesita vender más de 10 bolígrafos para ganar más de $20. Entonces la solución a la desigualdad es$x>10$.

Entradas en el glosario

Definición: Solución a una desigualdad

Una solución a una desigualdad es un número que se puede utilizar en lugar de la variable para hacer realidad la desigualdad.

Por ejemplo, 5 es una solución a la desigualdad$c<10$, porque es cierto que$5<10$. Algunas otras soluciones a esta desigualdad son 9.9, 0 y -4.

Practica

Ejercicio$\PageIndex{4}$

La solución a$5-3x>35$ es$x>-10$ o bien$-10>x$. ¿Cuál es la solución correcta? Explique cómo sabe.

Ejercicio$\PageIndex{5}$

El director de la banda escolar determinó por experiencia pasada que si cobran$t$ dólares por un boleto para el concierto, pueden esperar la asistencia de$1000-50t$. El director utilizó este modelo para averiguar que el precio del boleto necesita ser de $8 o más para que asistan al menos 600. ¿Está de acuerdo con esta afirmación? ¿Por qué o por qué no?

Ejercicio$\PageIndex{6}$

¿Qué desigualdad es verdadera cuando el valor de$x$ es -3?

$-x-6<-3.5$
$-x-6>3.5$
$-x-6>-3.5$
$x-6>-3.5$

(De la Unidad 6.3.1)

Ejercicio$\PageIndex{7}$

Dibuja el conjunto de soluciones para cada una de las siguientes desigualdades.

1. $x\leq 5$

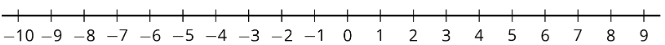
2. $x<\frac{5}{2}$

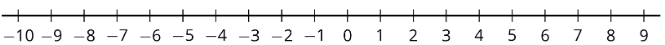
(De la Unidad 6.3.1)

Ejercicio$\PageIndex{8}$

Escribe tres ecuaciones diferentes que coincidan con el diagrama de cinta.

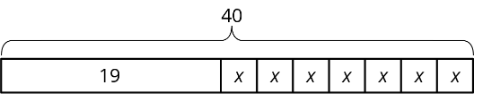
(De la Unidad 6.1.3)

Ejercicio$\PageIndex{9}$

Un panadero quiere reducir la cantidad de azúcar en sus recetas de pasteles. Decide reducir la cantidad utilizada en 1 pastel por$\frac{1}{2}$ taza. Luego usa$4\frac{1}{2}$ tazas de azúcar para hornear 6 pasteles.

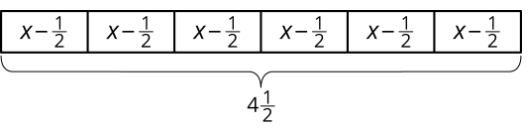
Describir cómo el diagrama de cinta representa la historia.
¿Cuánto azúcar había originalmente en cada receta de pastel?

(De la Unidad 6.1.2)

Ejercicio$\PageIndex{10}$

Hace un año, Clare medía 4 pies y 6 pulgadas de alto. Ahora Clare mide 4 pies y 10 pulgadas de alto. ¿En qué porcentaje aumentó la altura de Clare en el último año?

(De la Unidad 4.3.3)