6.3.3: Resolver de manera eficiente las
- Page ID
- 119042
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Lección
Resolvamos desigualdades más complicadas.
Ejercicio\(\PageIndex{1}\): Lots of Negatives
Aquí hay una desigualdad:\(-x\geq -4\).
- Predice cómo crees que serán las soluciones en la línea numérica.
- Seleccione todos los valores que son soluciones para\(-x\geq -4\):
- \(3\)
- \(-3\)
- \(4\)
- \(-4\)
- \(4.001\)
- \(-4.001\)
- Grafique las soluciones a la desigualdad en la recta numérica:
Ejercicio\(\PageIndex{2}\): Inequalities with Tables
1. Investiguemos la desigualdad\(x-3>-2\).
| \(x\) | \(-4\) | \(-3\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) | \(3\) | \(4\) |
|---|---|---|---|---|---|---|---|---|---|
| \(x-3\) | \(-7\) | \(-5\) | \(-1\) | \(1\) |
- Completa la tabla.
- ¿Para qué valores de\(x\) es cierto eso\(x-3=-2\)?
- ¿Para qué valores de\(x\) es cierto eso\(x-3>-2\)?
- Grafique las soluciones a\(x-3>-2\) en la recta numérica:
2. Aquí hay una desigualdad:\(2x<6\).
- Predecir qué valores de\(x\) harán\(2x<6\) verdadera la desigualdad.
- Completa la tabla. ¿Coincide con tu predicción?
\(x\) \(-4\) \(-3\) \(-2\) \(-1\) \(0\) \(1\) \(2\) \(3\) \(4\) \(2x\) Mesa\(\PageIndex{2}\) - Grafique las soluciones a\(2x<6\) en la recta numérica:
3. Aquí hay una desigualdad:\(-2x<6\).
- Predecir qué valores de\(x\) harán\(-2x<6\) verdadera la desigualdad.
- Completa la tabla. ¿Coincide con tu predicción?
\(x\) \(-4\) \(-3\) \(-2\) \(-1\) \(0\) \(1\) \(2\) \(3\) \(4\) \(-2x\) Mesa\(\PageIndex{4}\) - Grafique las soluciones a\(-2x<6\) en la recta numérica:
d. ¿En qué se\(2x<6\) diferencian las soluciones de las soluciones a\(-2x<6\)?
Ejercicio\(\PageIndex{3}\): Which Side are the Solutions?
1. Investiguemos\(-4x+5\geq 25\).
- Resolver\(-4x+5=25\).
- ¿Es\(-4x+5\geq 25\) verdad cuando\(x\) es 0? ¿Y cuándo\(x\) es\(7\)? ¿Y cuándo\(x\) es\(-7\)?
- Grafique las soluciones a\(-4x+5\geq 25\) en la recta numérica.
2. Investiguemos\(\frac{4}{3}x+3<\frac{23}{3}\).
- Resolver\(\frac{4}{3}x+3=\frac{23}{3}\).
- ¿Es\(\frac{4}{3}x+3<\frac{23}{3}\) verdad cuándo\(x\) es\(0\)?
- Grafique las soluciones a\(\frac{4}{3}x+3<\frac{23}{3}\) en la recta numérica.
3. Resuelve la desigualdad\(3(x+4)>17.4\) y grafica las soluciones en la recta numérica.
4. Resuelve la desigualdad\(-3\left(x-\frac{4}{3}\right)\leq 6\) y grafica las soluciones en la recta numérica.
¿Estás listo para más?
Escribir al menos tres desigualdades distintas cuya solución sea\(x>-10\). Encuentra uno con\(x\) en el lado izquierdo que use un\(<\).
Resumen
Aquí hay una desigualdad:\(3(10-2x)<18\). La solución a esta desigualdad son todos los valores que podrías usar en lugar de\(x\) hacer realidad la desigualdad.
Para resolver esto, primero podemos resolver la ecuación relacionada\(3(10-2x)=18\) para obtener la solución\(x=2\). Eso significa que 2 es el límite entre valores de que hacen verdadera la desigualdad y valores que hacen falsa la desigualdad.
Para resolver la desigualdad, podemos verificar números mayores que 2 y menores que 2 y ver cuáles hacen que la desigualdad sea cierta.
Comprobemos un número que sea mayor a 2:\(x=5\). Sustituyendo\(x\) con 5 en la desigualdad, obtenemos\(3(10-2\cdot 5)<18\) o simplemente\(0<18\). Esto es cierto, también lo\(x=5\) es una solución. Esto quiere decir que todos los valores mayores a 2 hacen que la desigualdad sea cierta. Podemos escribir las soluciones como\(x>2\) y también representar las soluciones en una línea numérica:
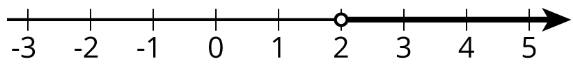
Observe que 2 en sí no es una solución porque es el valor de lo\(x\) que hace\(3(10-2x)\) igual a 18, y así no hace\(3(10-2x)<18\) verdad.
Para confirmar que encontramos la solución correcta, también podemos probar un valor que es menor a 2. Si probamos\(x=0\), obtenemos\(3(10-2\cdot 0)<18\) o simplemente\(30<18\). Esto es falso, así\(x=0\) y todos los valores de\(x\) que son menores a 2 no son soluciones.
Entradas en el glosario
Definición: Solución a una desigualdad
Una solución a una desigualdad es un número que se puede utilizar en lugar de la variable para hacer realidad la desigualdad.
Por ejemplo, 5 es una solución a la desigualdad\(c<10\), porque es cierto que\(5<10\). Algunas otras soluciones a esta desigualdad son 9.9, 0 y -4.
Practica
Ejercicio\(\PageIndex{4}\)
- Consideremos la desigualdad\(-1\leq \frac{x}{2}\).
- Predecir qué valores de\(x\) harán verdadera la desigualdad.
- Completa la tabla para verificar tu predicción.
\(x\) \(-4\) \(-3\) \(-2\) \(-1\) \(0\) \(1\) \(2\) \(3\) \(4\) \(\frac{x}{2}\) Mesa\(\PageIndex{5}\)
- Consideremos la desigualdad\(1\leq\frac{-x}{2}\).
- Predecir qué valores de lo\(x\) harán realidad.
- Completa la tabla para verificar tu predicción.
\(x\) \(-4\) \(-3\) \(-2\) \(-1\) \(0\) \(1\) \(2\) \(3\) \(4\) \(-\frac{x}{2}\) Mesa\(\PageIndex{6}\)
Ejercicio\(\PageIndex{5}\)
Diego está resolviendo la desigualdad\(100-3x\geq -50\). Él resuelve la ecuación\(100-3x=-50\) y obtiene\(x=50\). ¿Cuál es la solución a la desigualdad?
- \(x<50\)
- \(x\leq 50\)
- \(x>50\)
- \(x\geq 50\)
Ejercicio\(\PageIndex{6}\)
Resuelva la desigualdad\(-5(x-1)>-40\) y grafique la solución en una recta numérica.
Ejercicio\(\PageIndex{7}\)
Seleccionar todos los valores\(x\) que hagan\(-x+6\geq 10\) realidad la desigualdad.
- \(-3.9\)
- \(4\)
- \(-4.01\)
- \(-4\)
- \(4.01\)
- \(3.9\)
- \(0\)
- \(-7\)
(De la Unidad 6.3.1)
Ejercicio\(\PageIndex{8}\)
Dibuja el conjunto de soluciones para cada una de las siguientes desigualdades.
1. \(x>7\)
2. \(x\geq -4.2\)
(De la Unidad 6.3.1)
Ejercicio\(\PageIndex{9}\)
El precio de un par de aretes es de 22 dólares pero Priya los compra a la venta por 13.20 dólares.
- ¿Por cuánto se descontó el precio?
- ¿Cuál fue el porcentaje del descuento?
(De la Unidad 4.3.3)