6.4.2: Expansión y Factoring

Última actualización
Guardar como PDF

Page ID: 118969

Illustrative Mathematics
OpenUp Resources

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Lección

Usemos la propiedad distributiva para escribir expresiones de diferentes maneras.

Ejercicio$\PageIndex{1}$: Number Talk: Parentheses

Encuentra mentalmente el valor de cada expresión.

$2+3\cdot 4$

$(2+3)(4)$

$2-3\cdot 4$

$2-(3+4)$

Ejercicio$\PageIndex{2}$: Factoring and Expanding with Negative Numbers

En cada fila, escriba la expresión equivalente. Si te quedas atascado, usa un diagrama para organizar tu trabajo. La primera fila se proporciona como ejemplo. Se proporcionan diagramas para las tres primeras filas.

Figura$\PageIndex{1}$: Tres diagramas de área, cada una de 1 fila, 2 columnas. Primer diagrama, fila etiquetada como negativo 3, columnas etiquetadas 5 y negativo 2y. Segundo diagrama, fila etiquetada 5, columnas etiquetadas como a y negativas 6. Tercer diagrama, fila etiquetada 2, cajas etiquetadas 6 a y negativo 2 b, espacios en blanco por encima de las columnas indicaron etiquetas faltantes.

Mesa$\PageIndex{1}$
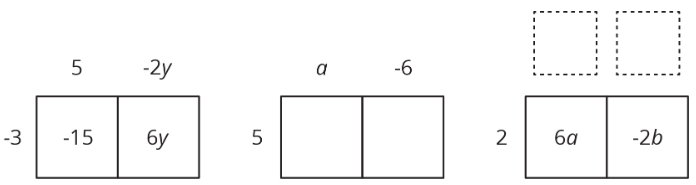
factorizado	ampliado
$-3(5-2y)$	$-15+6y$
$5(a-6)$
	$6a-2b$
$-4(2w-5z)$
$-2(2x-3y)$
	$20x-10y+15z$
$k(4-17)$
	$10a-13a$
$-2x(3y-z)$
	$ab-bc-3bd$
$-x(3y-z+4w)$

¿Estás listo para más?

Expanda para crear una expresión equivalente que utilice el menor número de términos:$((((x+1)\frac{1}{2})+1)\frac{1}{2})+1$. Si escribimos una nueva expresión siguiendo el mismo patrón para que hubiera 20 conjuntos de paréntesis, ¿cómo podría expandirse a una expresión equivalente que utilice el menor número de términos?

Resumen

Podemos usar propiedades de operaciones de diferentes maneras para reescribir expresiones y crear expresiones equivalentes. Ya hemos visto que podemos usar la propiedad distributiva para expandir una expresión, por ejemplo$3(x+5)=3x+15$. También podemos usar la propiedad distributiva en la otra dirección y factorizar una expresión, por ejemplo$8x+12=4(2x+3)$.

Podemos organizar el trabajo de usar la propiedad distributiva para reescribir la expresión$12x-8$. En este caso conocemos el producto y necesitamos encontrar los factores.

Los términos del producto van dentro:

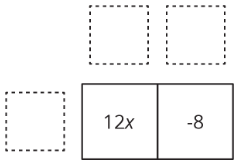
Miramos las expresiones y pensamos en un factor que tienen en común. $12x$y$-8$ cada uno tiene un factor de 4. Colocamos el factor común en un lado del rectángulo grande:

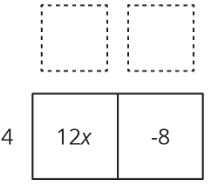
Ahora pensamos: “¿4 veces lo que es 12$x$?” “4 veces ¿qué es -8?” y escribe los otros factores en el otro lado del rectángulo:

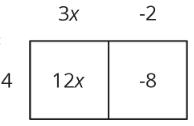
Entonces,$12x-8$ es equivalente a$4(3x-2)$.

Entradas en el glosario

Definición: Expandir

Para expandir una expresión, usamos la propiedad distributiva para reescribir un producto como suma. La nueva expresión es equivalente a la expresión original.

Por ejemplo, podemos expandir la expresión$5(4x+7)$ para obtener la expresión equivalente$20x+25$.

Definición: Factor (una expresión)

Para factorizar una expresión, utilizamos la propiedad distributiva para reescribir una suma como producto. La nueva expresión es equivalente a la expresión original.

Por ejemplo, podemos factorizar la expresión$20x+35$ para obtener la expresión equivalente$5(4x+7)$.

Definición: Término

Un término es parte de una expresión. Puede ser un solo número, una variable, o un número y una variable que se multiplican entre sí. Por ejemplo, la expresión$5x+18$ tiene dos términos. El primer término es$5x$ y el segundo es 18.

Practica

Ejercicio$\PageIndex{3}$

Expandir para escribir una expresión equivalente:$\frac{-1}{4}(-8x+12y)$
Factor para escribir una expresión equivalente:$36a-16$

Ejercicio$\PageIndex{4}$

Lin se perdió la clase de matemáticas el día en que trabajaron en la expansión y factorización. Kiran está ayudando a Lin a ponerse al día.

Lin entiende que expandirse es usar la propiedad distributiva, pero no entiende qué es el factoring o por qué funciona. ¿Cómo puede Kiran explicarle el factoring a Lin?
Lin le pregunta a Kiran cómo los diagramas con cajas ayudan a factorizar. ¿Qué debería decirle Kiran a Lin sobre las cajas?
Lin le pide a Kiran que la ayude a factorizar la expresión$-4xy-12xz+20xw$. ¿Cómo puede Kiran usar este ejemplo para que Lin entienda el factoring?

Ejercicio$\PageIndex{5}$

Completa la ecuación con números que hagan que la expresión en el lado derecho del signo igual sea equivalente a la expresión del lado izquierdo.

$75a+25b=\underline{\quad}(\underline{\quad}a+b)$

Ejercicio$\PageIndex{6}$

Elena hace su sombra favorita de pintura púrpura mezclando 3 tazas de pintura azul,$1\frac{1}{2}$ tazas de pintura roja y$\frac{1}{2}$ de una taza de pintura blanca. Elena tiene$\frac{2}{3}$ de una taza de pintura blanca.

Asumiendo que tiene suficiente pintura roja y pintura azul, ¿cuánta pintura púrpura puede hacer Elena?
¿Cuánta pintura azul y pintura roja necesitará Elena usar con la$\frac{2}{3}$ de una taza de pintura blanca?

(De la Unidad 4.1.3)

Ejercicio$\PageIndex{7}$

Resuelve cada ecuación.

$\frac{-1}{8}d-4=\frac{-3}{8}$
$\frac{-1}{4}m+5=16$
$10b+-45=-43$
$-8(y-1.25)=4$
$3.2(s+10)=32$

(De la Unidad 6.2.3)

Ejercicio$\PageIndex{8}$

Seleccionar todas las desigualdades que tengan las mismas soluciones que$-4x<20$.

$-x<5$
$4x>-20$
$$4x$
$$x$
$x>5$
$x>-5$

(De la Unidad 6.3.1)

factorizado	ampliado
\(-3(5-2y)\)	\(-15+6y\)
\(5(a-6)\)
	\(6a-2b\)
\(-4(2w-5z)\)
\(-2(2x-3y)\)
	\(20x-10y+15z\)
\(k(4-17)\)
	\(10a-13a\)
\(-2x(3y-z)\)
	\(ab-bc-3bd\)
\(-x(3y-z+4w)\)

Search

Text Color

Text Size

Margin Size

Font Type