Saltar al contenido principal
LibreTexts Español

8.2.2: Hacer un seguimiento de todos los resultados posibles

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    119074

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Lección

    Permite explorar espacios de muestra para experimentos con múltiples partes.

    Ejercicio\(\PageIndex{1}\): How Many Different Meals?

    ¿Cuántas comidas diferentes son posibles si cada comida incluye un plato principal, una guarnición y una bebida?

    platos principales guarniciones bebidas
    pollo a la parrilla ensalada leche
    sándwich de pavo salsa de manzana jugo
    ensalada de pasta \(\underline{\quad}\) agua
    Mesa\(\PageIndex{1}\)

    Ejercicio\(\PageIndex{2}\): Lists, Tables, and Trees

    Considera el experimento: Voltear una moneda, y luego rodar un cubo numérico.

    Elena, Kiran y Priya utilizan cada uno un método diferente para encontrar el espacio muestral de este experimento.

    • Elena escribe cuidadosamente una lista de todas las opciones: Cabezas 1, Cabezas 2, Cabezas 3, Cabezas 4, Cabezas 5, Cabezas 6, Tails 1, Tails 2, Tails 3, Tails 4, Tails 5, Tails 6.
    • Kiran hace una mesa:
      1 2 3 4 5 6
      H H1 H2 H3 H4 H5 H6
      T T1 T2 T3 T4 T5 T6
      Mesa\(\PageIndex{2}\)
    • Priya dibuja un árbol con ramas en el que cada camino representa un resultado diferente:
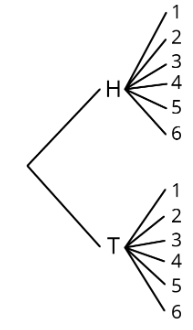
    clipboard_e4377bace35887b8b728ca88c0f862e3e.png
    Figura\(\PageIndex{1}\)
    1. Compara los tres métodos. ¿Qué es lo mismo de cada método? ¿Qué es diferente? Esté preparado para explicar por qué cada método produce todos los diferentes resultados sin repetir ninguno.
    2. ¿Qué método prefieres para esta situación?
      Haz una pausa aquí para que tu profesor pueda revisar tu trabajo.
    3. Encuentra el espacio muestral para cada uno de estos experimentos usando cualquier método. Asegúrese de enumerar todos los resultados posibles sin repetir ninguno.
      1. Voltear un centavo, luego voltear un centavo, y luego voltear un centavo. Registre si cada uno aterriza cabeza o cola hacia arriba.
      2. El clóset de Han tiene: una camisa azul, una camisa gris, una camisa blanca, pantalón azul, pantalón caqui y pantalón negro. Debe seleccionar una camisa y un par de pantalones para usar para el día.
      3. Girar un color, y luego girar un número.
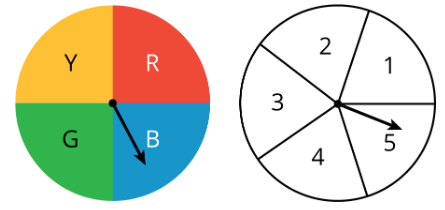
    clipboard_e8b5d5ca6a4b9e124ac09344709e2a6b0.png
    Figura\(\PageIndex{2}\)

    d. gire la manecilla de las horas en un reloj analógico, y luego elija a.m. o p.m.

    Ejercicio\(\PageIndex{3}\): How Many Sandwiches?

    1. Una tienda de sándwiches submarinos hace sándwiches con un tipo de pan, una proteína, una opción de queso y dos verduras. ¿Cuántos sándwiches diferentes son posibles? Explica tu razonamiento. No es necesario escribir el espacio de muestra.

    • Panes: Italiano, blanco, trigo
    • Proteínas: Atún, jamón, pavo, frijoles
    • Queso: Provolone, suizo, americano, ninguno
    • Verduras: Lechuga, tomates, pimientos, cebollas, encurtidos
    clipboard_e43c08672f9aaec0fc2d0e0080507261e.png
    Figura\(\PageIndex{3}\): Sándwich submarino y chips, de jeffreyw. CC POR 2.0. Wikimedia Commons. Fuente.

    2. Andre sabe que quiere un sándwich que tenga jamón, lechuga y tomates. No le importa el tipo de pan o queso. ¿Cuántos de los diferentes sándwiches harían feliz a Andre?

    3. Si se hace un sándwich eligiendo al azar cada una de las opciones, ¿cuál es la probabilidad de que sea un sándwich con el que Andre estaría contento?

    ¿Estás listo para más?

    Describir una situación que involucra tres partes y tiene un total de 24 resultados en el espacio muestral.

    Resumen

    A veces necesitamos una forma sistemática de contar el número de resultados que son posibles en una situación dada. Por ejemplo, supongamos que hay 3 personas (A, B y C) que quieren postularse para el presidente de un club y 4 personas diferentes (1, 2, 3 y 4) que quieren postularse para vicepresidente del club. Podemos usar un árbol, una mesa o una lista ordenada para contar cuántas combinaciones diferentes son posibles para que un presidente sea emparejado con un vicepresidente.

    Con un árbol, podemos comenzar con una rama para cada una de las personas que quieran ser presidente. Entonces para cada posible presidente, agregamos una rama por cada posible vicepresidente, para un total de\(3\cdot 4=12\) posibles parejas. También podemos comenzar contando primero a los vicepresidentes y luego sumando una rama por cada posible presidente, para un total de\(3\cdot 4=12\) posibles parejas.

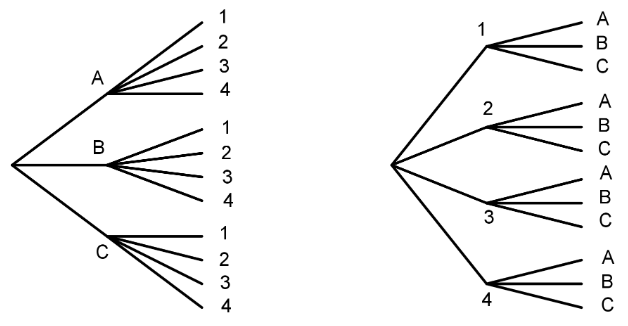
    clipboard_e1b9f6542a701a1294db4f351eca2b136.png
    Figura\(\PageIndex{4}\): Dos diagramas de árbol. El diagrama de árbol más a la izquierda tiene tres ramas para la primera opción, etiquetadas A, B y C. Las opciones A, B y C tienen cada una cuatro ramas etiquetadas con un número diferente de 1 a 4. El diagrama de árbol más a la derecha tiene cuatro ramas para la primera opción, etiquetadas con 1, 2, 3 y 4. Las opciones 1, 2, 3 y 4 tienen cada una tres ramas, etiquetadas con una letra A, B o C.

    Una tabla puede mostrar el mismo resultado:

    1 2 3 4
    A \(A, 1\) \(A, 2\) \(A, 3\) \(A, 4\)
    B \(B, 1\) \(B, 2\) \(B, 3\) \(B, 4\)
    C \(C, 1\) \(C, 2\) \(C, 3\) \(C, 4\)
    Mesa\(\PageIndex{3}\)

    Así lo hace esta lista ordenada:

    A1, A2, A3, A4, B1, B2, B3, B4, C1, C2, C3, C4

    Practica

    Ejercicio\(\PageIndex{4}\)

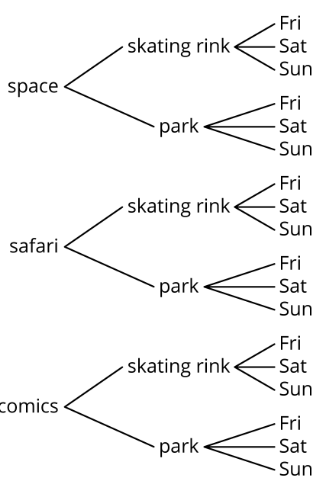
    Noah está planeando su fiesta de cumpleaños. Aquí hay un árbol que muestra todos los posibles temas, ubicaciones y días de la semana que Noé está considerando.

    1. ¿Cuántos temas está considerando Noé?
    2. ¿Cuántas ubicaciones está considerando Noah?
    3. ¿Cuántos días de la semana está considerando Noé?
    4. Una posibilidad que Noé está considerando es una fiesta con temática espacial en la pista de patinaje el domingo. Escribe otras dos posibles fiestas que Noé está considerando.
    5. ¿Cuántos resultados diferentes hay en el espacio muestral?
    clipboard_ef578ea61434a6c3d612d5598b61b94dd.png
    Figura\(\PageIndex{5}\): Un diagrama de árbol. En el primer nivel del árbol, las ramas son para los temas espacio, safari y cómics. En el segundo nivel del árbol, hay dos ramas de cada tema para las ubicaciones pista de patinaje o parque para un total de 6 ramas. En el tercer nivel del árbol, hay tres ramas de cada ubicación para los días viernes, sábado y domingo, para un total de 18 ramas.

    Ejercicio\(\PageIndex{5}\)

    Para cada evento, escriba el espacio de muestra y diga cuántos resultados hay.

    1. Lin selecciona un tipo de lechuga y un aderezo para hacer una ensalada.
      Tipos de lechuga: iceberg, lechuga romana
      Aderezos: rancho, italiano, francés
    2. Diego elige piedra, papel o tijeras, y Jada elige piedra, papel o tijeras.
    3. Girar estos 3 hilanderos.
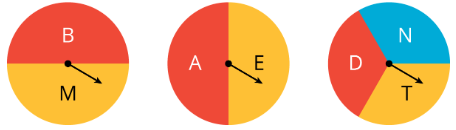
    clipboard_e86047bd076fc3a687126fa8555c338b8.png
    Figura\(\PageIndex{6}\): Tres hiladores circulares diferentes. El spinner más a la izquierda se divide en dos partes iguales: una etiquetada B y otra etiquetada M. El puntero está en la parte etiquetada M. La hilandera en el centro se divide en dos partes iguales: una etiquetada A y otra etiquetada E. El puntero está en la parte etiquetada E. La hilandera más a la derecha se divide en tres partes iguales: uno etiquetado D, uno etiquetado N y otro etiquetado T. El puntero está en la parte etiquetada T.

    Ejercicio\(\PageIndex{6}\)

    Se realiza una simulación para representar patear 5 goles de campo en un solo juego con un 72% de probabilidad de hacer cada uno. Un 1 representa hacer la patada y un 0 representa faltar la patada.

    juicio resultado
    1 10101
    2 11010
    3 00011
    4 11111
    5 10011
    Mesa\(\PageIndex{4}\)

    (De la Unidad 8.2.1)

    Ejercicio\(\PageIndex{7}\)

    Hay una bolsa de 50 canicas.

    • Andre saca una canica, graba su color y la vuelve a meter. En 4 juicios, obtiene una canica verde 1 vez.
    • Jada saca una canica, graba su color y la vuelve a meter. En 12 juicios, obtiene una canica verde 5 veces.
    • Noé saca una canica, registra su color y la vuelve a meter. En 9 juicios, obtiene una canica verde 3 veces.

    Estima la probabilidad de obtener una canica verde de esta bolsa. Explica tu razonamiento.

    (De la Unidad 8.1.4)

    This page titled 8.2.2: Hacer un seguimiento de todos los resultados posibles is shared under a CC BY license and was authored, remixed, and/or curated by Illustrative Mathematics.