Saltar al contenido principal
LibreTexts Español

8.2.3: Experimentos de varios pasos

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    119075

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Lección

    Veamos las probabilidades de experimentos que tienen múltiples pasos.

    Ejercicio\(\PageIndex{1}\): True or False?

    ¿Cada ecuación es verdadera o falsa? Explica tu razonamiento.

    \(8=(8+8+8+8)\div 3\)

    \((10+10+10+10+10)\div 5=10\)

    \(6+4+6+4+6+4)\div 6=5\)

    Ejercicio\(\PageIndex{2}\): Spinning a Color and Number

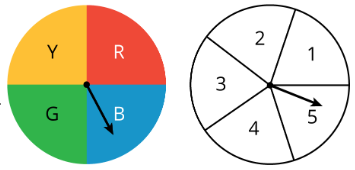
    El otro día, escribiste el espacio de muestra para hacer girar cada uno de estos hilanderos una vez.

    Cuál es la probabilidad de obtener:

    1. ¿Verde y 3?
    2. ¿Azul y algún número impar?
    3. ¿Algún color que no sea rojo y cualquier número que no sea 2?
    clipboard_eb0e3d719b92030b74581635b4401e140.png
    Figura\(\PageIndex{1}\): Dos hiladores circulares diferentes. El spinner de la izquierda se divide en cuatro partes iguales. La primera parte es roja y etiquetada con R, la segunda parte es azul y etiquetada con B, la tercera parte es verde y etiquetada con G, y la cuarta parte es amarilla y etiquetada Y. El puntero está en la parte etiquetada B. La hilandera de la derecha se divide en cinco partes iguales. Comenzando por la parte superior derecha, y moviéndose en sentido horario, la primera parte está etiquetada con 1, la segunda, 2, la tercera, 3, la cuarta, 4, y la quinta, 5. El puntero está en la parte etiquetada 5.

    Ejercicio\(\PageIndex{3}\): Cubes and Coins

    El otro día miraste una lista, una mesa y un árbol que mostraban el espacio de muestra para rodar un cubo numérico y voltear una moneda.

    1. Tu profesor te asignará una de estas tres estructuras para que las uses para responder a estas preguntas. Esté preparado para explicar su razonamiento.
      1. ¿Cuál es la probabilidad de obtener colas y un 6?
      2. ¿Cuál es la probabilidad de conseguir cabezas y un número impar?
        Haz una pausa aquí para que tu profesor pueda revisar tu trabajo.
    2. Supongamos que rueda dos cubos numéricos. Cuál es la probabilidad de obtener:
      1. ¿Ambos cubos muestran el mismo número?
      2. ¿Exactamente un cubo que muestra un número par?
      3. ¿Al menos un cubo que muestre un número par?
      4. Dos valores que tienen una suma de 8?
      5. Dos valores que tienen una suma de 13?
    3. Jada voltea tres cuartos. ¿Cuál es la probabilidad de que los tres aterricen mostrando el mismo lado?

    Ejercicio\(\PageIndex{4}\): Pick a Card

    Imagina que hay 5 tarjetas. Son de color rojo, amarillo, verde, blanco y negro. Mezclarás las cartas y seleccionas una de ellas sin mirar. Entonces, sin volver a poner esa carta, mezclas las cartas restantes y seleccionar otra.

    1. Escriba el espacio de muestra y diga cuántos resultados posibles hay.
    2. ¿Qué estructura utilizaste para escribir todos los resultados (lista, tabla, árbol, algo más)? Explica por qué elegiste esa estructura.
    3. ¿Cuál es la probabilidad de que:
      1. ¿Obtienes una tarjeta blanca y una tarjeta roja (en cualquier orden)?
      2. ¿Obtienes una tarjeta negra (cualquiera de las dos veces)?
      3. ¿No obtienes una tarjeta negra (ya sea el momento)?
      4. ¿Obtienes una tarjeta azul?
      5. ¿Obtienes 2 tarjetas del mismo color?
      6. ¿Obtienes 2 tarjetas de diferentes colores?

    ¿Estás listo para más?

    En un juego usando cinco cartas numeradas 1, 2, 3, 4 y 5, tomas dos cartas y sumas los valores juntos. Si la suma es 8, ganas. ¿Prefieres elegir una tarjeta y devolverla antes de recoger la segunda carta, o tener la tarjeta en tu mano mientras eliges la segunda carta? Explica tu razonamiento.

    Resumen

    Supongamos que tenemos dos bolsas. Uno contiene 1 bloque de estrellas y 4 bloques de luna. El otro contiene 3 bloques estelares y 1 bloque lunar.

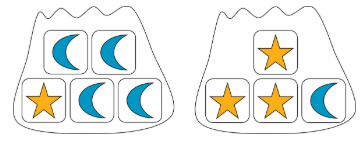
    clipboard_e3010445d2a954403e584a36518eb7a7e.png
    Figura\(\PageIndex{2}\)

    Si seleccionamos un bloque al azar de cada uno, ¿cuál es la probabilidad de que obtengamos dos bloques estelares o dos bloques lunares?

    Para responder a esta pregunta, podemos dibujar un diagrama de árbol para ver todos los posibles resultados.

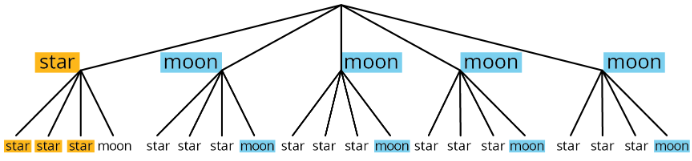
    clipboard_eb827ec32151bb8d362c45b5e65eda862.png
    Figura\(\PageIndex{3}\): Un diagrama de árbol. La primera opción tiene 5 ramas, que representan los 5 bloques en la bolsa: una rama está etiquetada como estrella, las otras 4 están etiquetadas como luna. Cada una de estas ramas tiene 4 ramas, que representan los 4 bloques en la segunda bolsa. 3 ramas están etiquetadas como estrella y una está etiquetada como luna. La palabra estrella en la primera opción, y las opciones de 3 estrellas que se ramifican de ella se destacan en oro. Desde la primera opción, la palabra luna se resalta en azul en cada una de las cuatro ramas restantes. De cada una de esas ramas, la única opción de luna para cada una también se resalta en azul.

    Hay\(5\cdot 4=20\) posibles resultados. De estas, 3 de ellas son ambas estrellas, y 4 son ambas lunas. Entonces la probabilidad de obtener 2 bloques estelares o 2 bloques lunares es\(\frac{7}{20}\).

    En general, si todos los resultados en un experimento son igualmente probables, entonces la probabilidad de un evento es la fracción de resultados en el espacio muestral para el que ocurre el evento.

    Practica

    Ejercicio\(\PageIndex{5}\)

    Una máquina expendedora tiene 5 colores (blanco, rojo, verde, azul y amarillo) de pelotas de goma y la misma posibilidad de dispensar cada una. Una segunda máquina tiene 4 diferentes bandas de goma en forma de animal (león, elefante, caballo y cocodrilo) y la misma oportunidad de dispensar cada una. Si compras un artículo de cada máquina, ¿cuál es la probabilidad de obtener un gumball amarillo y una banda de leones?

    Ejercicio\(\PageIndex{6}\)

    Los números del 1 al 10 se ponen en una bolsa. Los números del 5 al 14 se meten en otra bolsa. Cuando eliges un número de cada bolsa, ¿cuál es la probabilidad de que obtengas el mismo número?

    Ejercicio\(\PageIndex{7}\)

    Al rodar 3 cubos de números estándar, la probabilidad de que los tres números coincidan es\(\frac{6}{216}\). ¿Cuál es la probabilidad de que los tres números no coincidan todos? Explica tu razonamiento.

    Ejercicio\(\PageIndex{8}\)

    Para cada evento, escriba el espacio de muestra y diga cuántos resultados hay.

    1. Enrolle un cubo numérico estándar. Después voltea un cuarto.
    2. Seleccione un mes. Después seleccione 2020 o 2025.

    (De la Unidad 8.2.2)

    Ejercicio\(\PageIndex{9}\)

    En una gráfica del área de un cuadrado vs. su perímetro, se trazan algunos puntos.

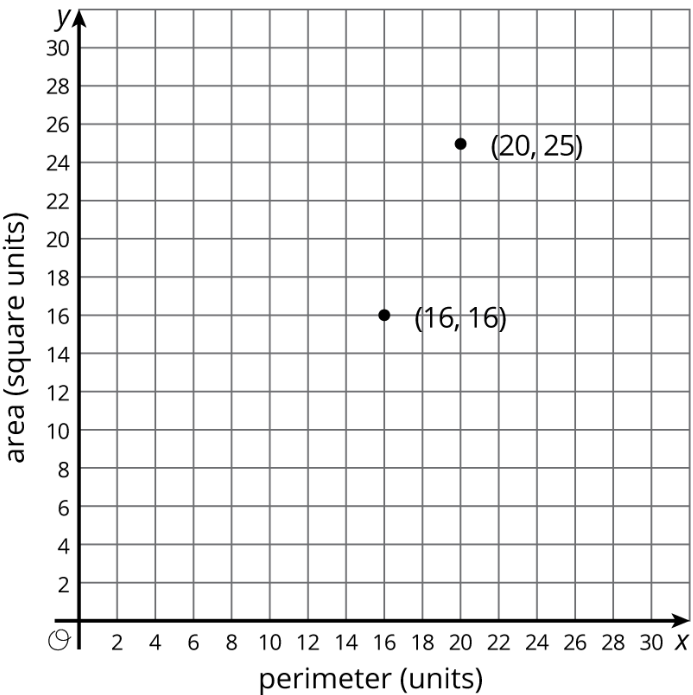
    clipboard_e0b57849406353b3dd32b5778a3993270.png
    Figura\(\PageIndex{4}\): Una rejilla de coordenadas con el eje horizontal etiquetado perímetro en unidades y eje vertical etiquetado área en unidades cuadradas. En ambos ejes se indican los números del 0 al 30, en incrementos de 2. Dos puntos con las coordenadas (16, 16) y (20, 25) se indican en la cuadrícula.
    1. Agrega algunos pares más ordenados a la gráfica.
    2. ¿Existe una relación proporcional entre el área y el perímetro de una plaza? Explica cómo sabes.

    (De la Unidad 2.4.2)

    This page titled 8.2.3: Experimentos de varios pasos is shared under a CC BY license and was authored, remixed, and/or curated by Illustrative Mathematics.