Saltar al contenido principal
LibreTexts Español

8.4.4: Comparando Poblaciones Usando Muestras

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    119116

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    Lección

    Comparemos diferentes poblaciones usando muestras.

    Ejercicio\(\PageIndex{1}\): Same Mean? Same MAD?

    Sin calcular, diga si cada par de conjuntos de datos tienen la misma media y si tienen la misma desviación media absoluta.

    1. conjunto A 1 3 3 5 6 8 10 14
      conjunto B 21 23 23 25 26 28 30 34
      Mesa\(\PageIndex{1}\)
    2. conjunto X 1 2 3 4 5
      conjunto Y 1 2 3 4 5 6
      Mesa\(\PageIndex{2}\)
    3. conjunto P 47 53 58 62
      conjunto Q 37 43 68 72
      Mesa\(\PageIndex{3}\)

    Ejercicio\(\PageIndex{2}\): With a Heavy Load

    Considera la pregunta: ¿Las mochilas de los estudiantes de décimo grado generalmente pesan más que las mochilas de los estudiantes de séptimo grado?

    Aquí hay gráficas de puntos que muestran los pesos de las mochilas para una muestra aleatoria de estudiantes de estos dos grados:

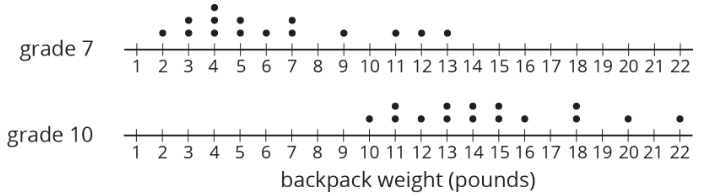
    clipboard_e8bad0e1ece5d16770be7cd5a0b870395.png
    Figura\(\PageIndex{1}\): Dos parcelas de puntos para el peso de la mochila en libras se etiquetan grado 7 y grado 10, y se indican los números 1 a 22. Los datos son los siguientes: Grado 7:2 libras, 1 punto. 3 libras, 2 puntos. 4 libras, 3 puntos. 5 libras, 2 puntos. 6 libras, 1 punto. 7 libras, 2 puntos. 9 libras, 1 punto. 11 libras, 1 punto. 12 libras, 1 punto. 13 libras, 1 punto. 13 libras, 1 punto. Grado 10:10 libras, 1 punto. 11 libras, 2 puntos. 12 libras, 1 punto. 13 libras, 2 puntos. 14 libras, 2 puntos. 15 libras, 2 puntos. 16 libras, 1 punto. 18 libras, 2 puntos. 20 libras, 1 punto. 22 libras, 1 punto.
    1. ¿Alguna mochila de séptimo grado en esta muestra pesaba más que una mochila de décimo grado?
    2. El peso medio de esta muestra de mochilas de séptimo grado es de 6.3 libras. ¿Crees que el peso medio de las mochilas para todos los estudiantes de séptimo grado es exactamente 6.3 libras?
    3. El peso medio de esta muestra de mochilas de décimo grado es de 14.8 libras. ¿Crees que hay una diferencia significativa entre el peso de todas las mochilas de estudiantes de séptimo y décimo grado? Explica o muestra tu razonamiento.

    Ejercicio\(\PageIndex{3}\): Do They Carry More?

    Aquí hay 10 muestras aleatorias más de pesos de mochila de estudiantes de séptimo grado.

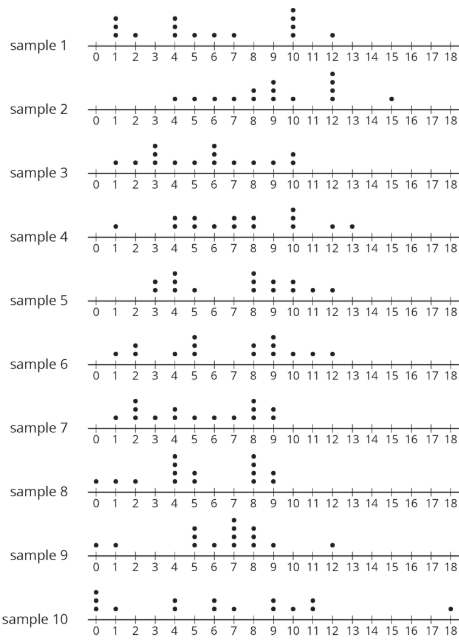
    clipboard_e46771988ea57f92f5cec87667ecbbfe1.png
    Figura\(\PageIndex{2}\): Diez parcelas de puntos tituladas muestra uno a muestra diez, cada uno con los números del 0 al 18 indicados.
    número de muestra peso medio (libras)
    1 5.8
    2 9.2
    3 5.5
    4 7.3
    5 7.2
    6 6.6
    7 5.2
    8 5.3
    9 6.3
    10 6.4
    Mesa\(\PageIndex{4}\)
      1. ¿Qué muestra tiene el peso medio más alto?
      2. ¿Qué muestra tiene el peso medio más bajo?
      3. ¿Cuál es la diferencia entre estas dos medias de muestra?
    2. Todas las muestras tienen una desviación media absoluta de aproximadamente 2.8 libras. Expresar la diferencia entre las medias de muestra más altas y más bajas como múltiplo de la MAD.
    3. ¿Estas muestras son muy diferentes? Explica o muestra tu razonamiento.
    4. Recuerde que nuestra muestra de mochilas de estudiantes de décimo grado tenía un peso promedio de 14.8 libras. El MAD para esta muestra es de 2.7 libras. Tu profesor te asignará una de las muestras de mochilas de estudiantes de séptimo grado para usar.
      1. ¿Cuál es la diferencia entre las medias de muestra para las mochilas de los estudiantes de décimo grado y las mochilas de los estudiantes de séptimo grado?
      2. Expresar la diferencia entre estas dos medias de muestra como un múltiplo del mayor de los MADs.
    5. ¿Crees que hay una diferencia significativa entre los pesos de todas las mochilas de estudiantes de séptimo y décimo grado? Explica o muestra tu razonamiento.

    Ejercicio\(\PageIndex{4}\): Steel From Different Regions

    Cuando los antropólogos encuentran artefactos de acero, pueden probar la cantidad de carbono en el acero para conocer a las personas que hicieron los artefactos. Aquí hay algunas gráficas de caja que muestran el porcentaje de carbono en muestras de acero que se encontraron en dos regiones diferentes:

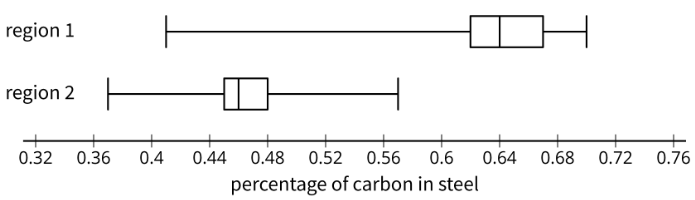
    clipboard_e378c9c8ade78052bb619e097605e8f1e.png
    Figura\(\PageIndex{3}\): Dos gráficas de caja desde 0 punto 32 hasta 0 punto 76 por 0 punto 4s. Trama de caja superior etiquetada región 1. Bigotes de aproximadamente 0 punto 41 a 48. Recuadro desde aproximadamente 0 punto 62 hasta aproximadamente 0 punto 67 con línea vertical en 0 punto 64. Bigotes desde aproximadamente 0 punto 67 hasta aproximadamente 0 punto 7. Gráfica de caja inferior etiquetada región 2. Bigotes de aproximadamente 0 punto 37 a 45. Recuadro desde aproximadamente 0 punto 45 hasta 0 punto 48 con línea vertical en aproximadamente 0 punto 46. Bigotes desde 0 punto 48 hasta aproximadamente 0 punto 57.
    1. Se encontró algún acero en la región 1 que tuviera:
      1. más carbono que algunos de los aceros que se encuentran en la región 2?
      2. menos carbono que algunos de los aceros encontrados en la región 2?
    2. ¿Crees que hay una diferencia significativa entre todos los artefactos de acero que se encuentran en las regiones 1 y 2?
    3. ¿Qué muestra tiene una distribución que no es aproximadamente simétrica?
    4. ¿Cuál es la diferencia entre las medianas de muestra para estas dos regiones?
      mediana de la muestra (%) IQR (%)
      región 1 \(0.64\) \(0.05\)
      región 2 \(0.47\) \(0.03\)
      Mesa\(\PageIndex{5}\)
    5. Expresar la diferencia entre estas dos medianas de muestra como un múltiplo del rango intercuartil más grande.
    6. Los antropólogos que realizaron el estudio concluyeron que había una diferencia significativa entre el acero de estas regiones. ¿Estás de acuerdo? Explica o muestra tu razonamiento.

    Resumen

    A veces queremos comparar dos poblaciones distintas. Por ejemplo, ¿hay una diferencia significativa entre los pesos de pugs y beagles? Aquí hay histogramas que muestran los pesos para una muestra de perros de cada una de estas razas:

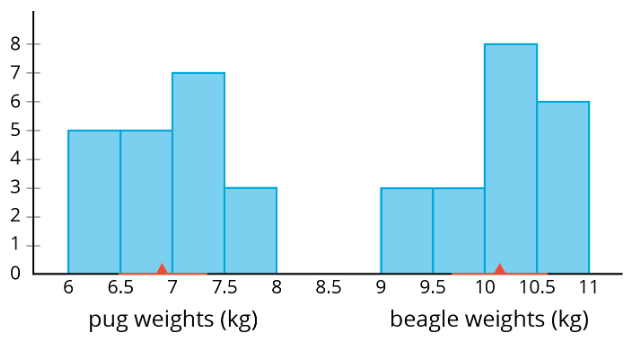
    clipboard_efc886fe953674089d1de755b369adcc6.png
    Figura\(\PageIndex{4}\): Un histograma para dos poblaciones diferentes: En el eje horizontal, se indican los números del 6 al 11, en incrementos del punto cero 5. Se indica la etiqueta pesos pug en kilogramos para los números del 6 al 8 y los pesos beagle en kilogramos para los números del 9 al 11. En el eje vertical se indican los números del 0 al 8. Los datos representados por las barras son los siguientes: Pesos Pug en kilogramos: Peso desde 6 hasta 6 punto 5, 5. Peso desde 6 punto 5 hasta 7, 5. Peso desde 7 hasta 7 punto 5, 7. Peso desde 7 punto 5 hasta 8, 3. Un triángulo se ubica en 6 punto 9 kilogramos. Pesos Beagle en kilogramos: Peso desde 9 hasta 9 punto 5, 3. Peso desde 9 punto 5 hasta 10, 3. Peso desde 10 hasta 10 punto 5, 8. Peso desde 10 punto 5 hasta 11, 6. Un triángulo se ubica en el punto 10 1.

    Los triángulos rojos muestran el peso medio de cada muestra, 6.9 kg para los pugs y 10.1 kg para los beagles. Las líneas rojas muestran los pesos que están dentro de 1 MAD de la media. Podemos pensar en estos como pesos “típicos” para la raza. Estos pesos típicos no se superponen. De hecho, la distancia entre las medias es\(10.1-6.9\) o 3.2 kg, ¡más de 6 veces la MAD más grande! Entonces podemos decir que hay una diferencia significativa entre los pesos de pugs y beagles.

    ¿Existe una diferencia significativa entre los pesos de los pugs machos y los pugs femeninos? Aquí hay diagramas de caja que muestran los pesos para una muestra de pugs macho y hembra:

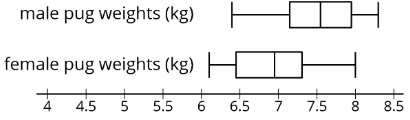
    clipboard_e45f1e48b17c1a402597ff8d77c535730.png
    Figura\(\PageIndex{5}\): Se indican dos parcelas de caja etiquetadas con pesos de pug macho en kilogramos y pesos de pug hembra en kilogramos. Se indican los números del 4 al 8 punto 5, en incrementos del punto cero 5. El resumen de cinco números para las parcelas de caja es el siguiente: Pesos de pug machos en kilogramos: Valor mínimo, 6 punto 4. Valor máximo, 8 punto 3. Q1, 7 punto 2. Q2, 7 punto 6. Q3, 7 punto 9. Pesos de pug hembra en kilogramos: Valor mínimo, 6 punto 2. Valor máximo, 8. Q1, 6 punto 4. Q2, 6 punto 9. Q3, 7 punto 3.

    Podemos ver que las medianas son diferentes, pero los pesos entre el primer y tercer cuartiles se superponen. A partir de estas muestras, diríamos que no hay una diferencia significativa entre los pesos de los pugs machos y los pugs hembras.

    En general, si las medidas de centro para dos muestras son al menos dos medidas de variabilidad separadas, decimos que la diferencia en las medidas de centro es significativa. Visualmente, esto significa que el rango de valores típicos no se superpone. Si están más cerca, entonces no consideramos que la diferencia sea significativa.

    Entradas en el glosario

    Definición: Rango intercuartílico (IQR)

    El rango intercuartílico es una forma de medir qué tan extendido está un conjunto de datos. A esto a veces lo llamamos el IQR. Para encontrar el rango intercuartil restamos el primer cuartil del tercer cuartil.

    Por ejemplo, el IQR de este conjunto de datos es 20 porque\(50-30=20\).

    22 29 30 31 32 43 44 45 50 50 59
    Q1 Q2 Q3
    Mesa\(\PageIndex{6}\)

    Definición: Proporción

    Una proporción de un conjunto de datos es la fracción de los datos en una categoría dada.

    Por ejemplo, una clase cuenta con 18 alumnos. Hay 2 estudiantes zurdos y 16 estudiantes diestros en la clase. La proporción de estudiantes que son zurdos es\(\frac{2}{20}\), o 0.1.

    Practica

    Ejercicio\(\PageIndex{5}\)

    Lin quiere saber si los estudiantes de primaria generalmente pasan más tiempo jugando al aire libre que los estudiantes en la secundaria. Ella selecciona una muestra aleatoria de talla 20 de cada población de estudiantes y les pregunta cuántas horas jugaron al aire libre la semana pasada. Supongamos que el MAD para cada una de sus muestras es de aproximadamente 3 horas.

    Seleccionar todos los pares de medias muestrales para las cuales Lin podría concluir que existe una diferencia significativa entre las dos poblaciones.

    1. escuela primaria: 12 horas, escuela media: 10 horas
    2. escuela primaria: 14 horas, escuela media: 9 horas
    3. escuela primaria: 13 horas, escuela media: 6 horas
    4. escuela primaria: 13 horas, escuela media: 10 horas
    5. escuela primaria: 7 horas, escuela media: 15 horas

    Ejercicio\(\PageIndex{6}\)

    Estas dos parcelas de caja muestran las distancias de un salto de pie, en pulgadas, para una muestra aleatoria de niños de 10 años y una muestra aleatoria de jóvenes de 15 años.

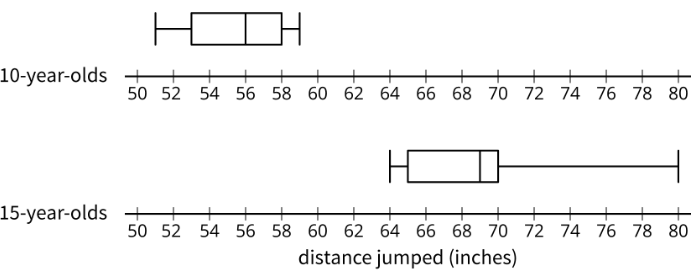
    clipboard_e20290b61fa97733fcb2ed36d63d568d0.png
    Figura\(\PageIndex{6}\): Dos parcelas de caja de 50 a 80 por 2s. Parcela de caja superior etiquetada con 10 años de edad. Bigotes del 51 al 53. Caja de 53 a 58 con línea vertical a 56. Bigotes del 58 al 59. Parcela de caja inferior etiquetada 15 años de edad. Bigotes del 64 al 65. Caja de 65 a 70 con línea vertical en 69. Bigotes del 70 al 80.

    ¿Existe una diferencia significativa en la distancia media para las dos poblaciones? Explique cómo sabe.

    Ejercicio\(\PageIndex{7}\)

    El ingreso medio para una muestra de personas de Chicago es de unos 60.000 dólares y el ingreso medio para una muestra de personas de Kansas City es de unos 46.000 dólares, pero los investigadores han determinado que no hay una diferencia significativa en las medianas. Explique por qué los investigadores podrían estar en lo cierto.

    Ejercicio\(\PageIndex{8}\)

    Un agricultor cultiva 5,000 calabazas cada año. Las calabazas tienen un precio de acuerdo a su peso, por lo que al agricultor le gustaría estimar el peso medio de las calabazas que cultivó este año. Selecciona al azar 8 calabazas y las pesa. Aquí están los pesos (en libras) de estas calabazas:

    \(2.9\quad 6.8\quad 7.3\quad 7.7\quad 8.9\quad 10.6\quad 12.3\quad 15.3\)

    1. Estimar el peso medio de las calabazas que cultivó el agricultor.

    Esta gráfica de puntos muestra el peso medio de 100 muestras de ocho calabazas, similar a la anterior.

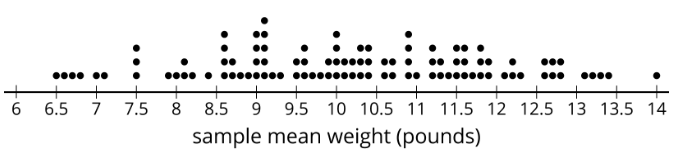
    clipboard_ee9425910f4947eb1f744dff5bc1b2a8e.png
    Figura\(\PageIndex{7}\)

    2. ¿Cuál parece ser el peso medio de las 5,000 calabazas?

    3. ¿Qué sugiere la gráfica de puntos de las medias de la muestra sobre cuán precisa podría ser una estimación basada en una sola muestra de 8 calabazas?

    4. ¿Qué cree que podría hacer el agricultor para obtener una estimación más precisa de la población?

    (De la Unidad 8.4.3)

    This page titled 8.4.4: Comparando Poblaciones Usando Muestras is shared under a CC BY license and was authored, remixed, and/or curated by Illustrative Mathematics.