1.1: Propiedades de Exponente y Más!
- Page ID
- 115900


La gente recuerda, sobre todo, ¡propiedades de las matemáticas! Las propiedades nos permiten transformar una expresión o una ecuación en una forma equivalente. A menudo necesitamos usar propiedades para movernos por la solución de un problema. Esta sección introduce varias propiedades. Para todas las propiedades de esta sección, las variables\(a\),\(b\), y\(c\) representan números reales. Aquí hay algunas propiedades, seguidas de ejemplos para su uso:
\[a + b = b+ a\]
El orden de adición no importa.
\[ab = ba\]
El orden de multiplicación no importa.
Evaluar\(40 + −6 + 12 + 6 + −40\)
Solución
La propiedad conmutativa de adición nos permite agregar en cualquier orden.
\(\begin{array} &&40 + −40 + 6 + −6 + 12 &\text{Rearrange the order to group opposites.} \\ &= 0 + 0 + 12 &\text{Opposites sum to zero.} \\ &= 12 \end{array}\)
¿Por qué es\(20\%\)\(45\) de lo mismo que\(45\%\) de\(20\)?
Solución
Verifiquemos que las dos expresiones son equivalentes:
\(\begin{array} &&0.20 \cdot 45 = 9 &\text{\(20\%\)de\(45\) es\(9\).}\\ &0.45\ cdot 20 = 9 &\ texto {\(45\%\)de\(20\) es\(9\).} \ end {array}\)
La propiedad conmutativa de la multiplicación nos dice por qué es verdad.
\(\begin{array} &&20 \cdot 0.01 \cdot 45 = 45 \cdot 0.01 \cdot 20 &\text{The order of multiplication is just rearranged.} \end{array}\)
La propiedad conmutativa, como se demostró, muestra por qué se mantiene la equivalencia.
¡Precaución! El orden de división y resta importa. Por lo tanto, la propiedad conmutativa sólo se aplica a la multiplicación y suma, NO a la división ni a la resta.
\[a(b+c) = ab + ac\]
La propiedad distributiva se puede visualizar como un área rectangular que es la suma de dos áreas rectangulares más pequeñas:
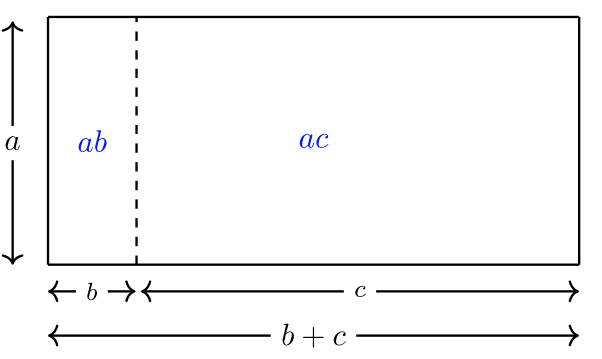
Simplificar\(6(2x + 7)\)
Solución
\(\begin{array}&&6(2x + 7) = 6(2x) + 6(7) \\ &= 12x + 42 \end{array}\)
\[x^a \cdot x^b = x^{a+b}\]
Hay muchas propiedades de potencia. Entender por qué se mantiene cada propiedad te ayudará a decidir si sumar o multiplicar exponentes. He aquí por qué la propiedad del producto tiene:
\( \underbrace{\underbrace{x \cdot x \cdot x \cdot x \cdot ... \cdot x}_{\text{\(a\)número de\(x\)'s}}\ cdot\ underbrackets {x\ cdot x\ cdot x\ cdot x\ cdot x\ cdot... \ cdot x} _ {\ texto {\(b\)número de\(x\)'s}}} _ {\ texto {\(a+b\)número de\(x\)}} = x^a\ cdot x^b = x^ {a+b}\)
\[(x^a)^b) = x^{ab}\]
Una vez más, entender por qué la propiedad tiene le ayudará a dominar la regla:
\(\underbrace{x^a \cdot x^a \cdot x^a \cdot x^a \cdot ... \cdot x^a}_{\text{\(b\)número de\(x^a\)'s}} =\ underbrackets {x^ {a+a+a+... +a}} _ {\ text {Producto de Poderes Propiedad}} =\ underbrackets {\ underbrackets {x^ {ba}} _ {a+a+a+... +a\; =\; ba}} _ {\ text {\(b\)número de\(a\)'s}} = x^ {ab}\)
Simplifica cada una de las siguientes expresiones.
- \(5y^8 \cdot y^4 \cdot y\)
- \(9(d^2)^3\)
- \(6u \cdot 3u^4 + (u^3)^2\)
Solución
- Producto de Poderes Propiedad
\(\begin{array} &&5y^8 \cdot y^4 \cdot y \\ &= 5 \cdot y^{8+4+1} \\ &= 5y^{13} \end{array}\)
- Poder de un Poder
\(\begin{array} &&9(d^2)^3 \\ &= 9d^{2 \cdot 3} \\ &= 9d^6 \end{array}\)
- Se utilizan ambas propiedades:
\(\begin{array} &&6u \cdot 3u^4 + (u^3)^2 \\ &= 6 \cdot 3 \cdot u^{1+4} \cdot u^{3 \cdot 2} \\ &= 18u^5 + u^6 \end{array}\)
La suma de poderes sólo puede simplificarse si las potencias son idénticas en base y exponente. Por ejemplo,\(x^3 + 7x^3 = (1 + 7)x^3 = 8x^3\). Simplifica combinando términos similares. De lo contrario, los poderes no pueden simplificarse. Ver solución al Ejemplo 4c.
\[(xy)^{a} = x^a \cdot y^a\]
Cada factor dentro de los paréntesis se eleva a la potencia indicada.
\[b^{-n} = \left( \dfrac{1}{b} \right)^{n} = \dfrac{1}{b^n} \]
Crear el recíproco de base\(b\), luego elevar\(b\) al poder positivo,\(n\).
Piensa en el exponente negativo como si estuviera marcando el poder, haciéndole saber que está en el lugar equivocado.

Simplifica cada una de las siguientes expresiones.
- \((3n)^4\)
- \(2(−4x^3y^2z)^2\)
- \((−2u^{−3}w^5 )^{−4}\)
Solución
- \(\begin{array} &&(3n)^4 \\ &=3^n \cdot 4^n \\ &=81n^4 \end{array}\)
- \(\begin{array} &&2(−4x^3y^2z)^2 \\ &=2(−4)^2 (x^3)^2(y^2)^2 (z)^2 \\ &=2 \cdot 16 \cdot x^{3 \cdot 2} \cdot y^{2 \cdot 2} \cdot z^2 \\ &= 32x^6y^4z^2 \end{array}\)
- \(\begin{array} &&(−2u^{−3}w^5 )^{−4} \\ &= (-2)^{-4} \cdot (u^{-3})^{-4} \cdot (w^5)^{-4} \\ &= \dfrac{1}{-2^4} \cdot u^{(-3)(-4)} \cdot w^{(5)(-4)} \\ &=\dfrac{u^{12}}{16w^{20}} \end{array}\)
\[\left( \dfrac{a}{b} \right)^{n} = \dfrac{a^n}{b^n}\]
La potencia se aplica tanto al numerador como al denominador.
Simplificar\(\left( \dfrac{5a^{-1}b^2}{2c^6} \right)^{-2}\)
Solución
Abordemos la solución como pelar una cebolla, comenzando por la capa externa:
\(\begin{array} &&=\left(\dfrac{2c^6}{5a^{-1}b^2}\right)^{2} &\text{The reciprocal of the fraction is taken. The power becomes positive.} \\ &= \left(\dfrac{2ac^6}{5b^2}\right)^{2} &\text{The negative exponent flags the power. \(\dfrac{1}{a^{-1}} = \dfrac{1}{\frac{1}{a}} = 1 \cdot a = a\)}\\ &=\ left (\ dfrac {(2ac^6) ^2} {(5b^2) ^2}\ right) &\ text {Se aplica el poder de una propiedad de cociente.}\\ &=\ dfrac {2^2\ cdot a^2\ cdot (c^6) ^2} {5^2\ cdot (b^2) ^2} &\ text {Se aplica el poder de una propiedad de producto.}\\ &=\ dfrac {4a^2c^ {12}} {25b^4} &\ text {El poder de un poder Se aplica propiedad. Todo está simplificado.} \ end {array}\)
\[\dfrac{x^a}{x^b} = x^{a-b} \]
Los exponentes se restan se debe a la cancelación de factores comunes. Por ejemplo,\(\dfrac{x^5}{x^3} = \dfrac{\cancel{x} \cdot \cancel{x} \cdot \cancel{x} \cdot x \cdot x}{\cancel{x} \cdot \cancel{x} \cdot \cancel{x}} = \dfrac{x \cdot x}{1} =x^2 = x^{5-3} \). Del mismo modo,\(\dfrac{x^3}{x^5} = \dfrac{\cancel{x} \cdot \cancel{x} \cdot \cancel{x}}{\cancel{x} \cdot \cancel{x} \cdot \cancel{x} \cdot x \cdot x} = \dfrac{1}{x \cdot x} =x^{-2} = x^{3-5} \)
Simplificar\(\left( \dfrac{4p^3q}{2p^2q^5} \right)^2\)
Solución
\(\begin{array} &&=\left( \dfrac{4}{2} \cdot p^{3-2} \cdot q^{1-5} \right)^2 &\text{The Quotient of Powers Property is applied.}\\ &=(2pq^{-4})^2 \text{The exponents are simplified.} \\ &=2^2 \cdot p^2 \cdot (q^{-4})^2 &\text{The Power of a Product Property is applied.} \\ &=4p^2q^{(-4)(2)} &\text{The Power of a Power Property is applied.} \\ &=4p^2q^{-8} &\text{The negative exponent flags the power \(q^8\).}\\ &=\ dfrac {4p^2} {q^8} &\ text {El poder\(q^8\) pertenece al denominador. Todo está simplificado.} \ end {array}\)
¡Pruébalo! (Ejercicios)
1. Nombra la propiedad que demuestra la ecuación.
- \((5 \cdot 7)^2 = 5^2 \cdot 7^2\)
- \(5(−20 + 2) = 5(−20) + 5(2)\)
- \(7(x + 1) = (x + 1) \cdot 7\)
- \(6^{12} \cdot 6^3 = 6^{15}\)
- \(8 + (−9) = −9 + 8\)
- \(4^{30} = (4^5)^6\)
2. Evaluar la siguiente suma. Reorganice los términos para que no sea necesaria una calculadora.
- \(12 + 84 + (−1) + (−84) + (−12) + 10\)
- \((−1.9) + (−5.8) + 13.2 + 1.9 + 5.8 + (−1.2)\)
Para #3 -11, use la propiedad distributiva para simplificar.
- \(10(7x + 9)\)
- \(2y^2 (8 + 2y)\)
- \(−7p(4p^4 + 1)\)
- \(3b[b^3 + (−2)]\)
- \(4u(5u^2 + 9u − 1)\)
- \(n^3m(2n^4m − 9nm^2 + 8)\)
- \(\dfrac{1}{2} \left( \dfrac{3}{4} − z^2 \right)\)
- \(\dfrac{2}{5} q^2 (5q + 10)\)
- \(\dfrac{7}{8} t(2t^2 − 4t + 3)\)
12. La propiedad conmutativa se aplica a la suma y multiplicación. La propiedad conmutativa NO aplica a la resta ni a la división. El símbolo ≠ significa “no es igual”. Mostrar que los dos lados de la desigualdad producen resultados diferentes.
- \(6 − 2 ≠ 2 − 6\)
- \(10 ÷ 5 ≠ 5 ÷ 10\)
Para #13 -15, use propiedades de potencia para simplificar. Las respuestas deben contener solo exponentes positivos.
- \((3n)^2 + (5n)(6n)\)
- \(( 5x^3 2y )^3\)
- \((−3a^5b^{−2}c)^4\)
16. La notación científica, aunada a reglas para exponentes, facilita los cálculos con números muy grandes y muy pequeños. Utilice las propiedades de potencia para evaluar cada uno de los siguientes. Deja tu respuesta en notación científica. Dejar poderes negativos de\(10\) como está para la respuesta final.
- \((6.02 x 10^{24})(1.3 x 10^{15})\)
- \((3.14 x 10^{10})(2.65 x 10^{18})\)
- \((7.4 x 10^{−6} )(1.25 x 10^{−4} )\)
- \((3.8 x 10^{−16})(2.4 x 10^{−8} )\)
Para #17 -25, use propiedades de potencia para simplificar. Las respuestas deben contener solo exponentes positivos. Usa fracciones, no decimales.
- \(\dfrac{12w^6}{4w}\)
- \(\dfrac{5u^2}{10u^3}\)
- \(\left( \dfrac{5}{4} \right)^{−1}\)
- \(\left( \dfrac{6t}{3} \right)^{−2}\)
- \(\left( \dfrac{4n^6}{2n} \right)^{−1}\)
- \(\left( \dfrac{7pq^5}{28p^3q} \right)^{2}\)
- \(\left( \dfrac{12x^{10}y^3}{24x^9y^8} \right)^{3}\)
- \(\left( \dfrac{9ab^{12}c^4}{27a^7bc^3} \right)^{−4}\)
- \(\left( \dfrac{6r^5 s^{−2}}{15r^{−1}s} \right)^{−3}\)
Para #26 -35, simplifique el uso de propiedades.
- \(2(3x + 10) + 5(2x − 1)\)
- \(4a^3 (a + 1) − 2a^2 (a^2 − a)\)
- \((8y^2 ) 2 − 3(7y^3 )(2y)\)
- \((4d)(9d^3)(2d^2) − (5d^3)^2\)
- \(\dfrac{1}{2} b^4 (6b − 2) − (3b^2 )^2\)
- \(\dfrac{3}{4} uv(8u − 4v) + \dfrac{3}{2} u \left(uv + \dfrac{2v}{u} \right)\)
- \(p^2q(4p + 3q) − (2pq)^2\)
- \(5mn^2 (m − n) − 4m^2 (n^2 − 1)\)
- \(10c^8 (2c^{−3} + c^{−4}) + c^{−2} (c^6 − 12c^7 )\)
- \(3n^7 (3n^{−2} )^{−1} + 2n^8 (n − 1) + (-n^{3} )^3\)


