Saltar al contenido principal
LibreTexts Español

1.2: Método FOIL y Productos Especiales

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    115892

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    En esta sección se dan ejemplos para multiplicar un binomio (polinomio\(2\) -término) por otro binomio. En algunos casos, el método FOIL produce patrones predecibles. A estos los llamamos “productos especiales”. Reconocer productos especiales será útil cuando volvamos a resolver ecuaciones cuadráticas.

    Los números reales informan cómo y por qué funcionan las reglas dentro de las expresiones algebraicas. Por esa razón, examinemos cómo multiplicar los números reales:\(53 \times 27\).

    Podrías completar el problema usando un enfoque tradicional aprendido en la escuela primaria. Este enfoque se muestra a continuación.

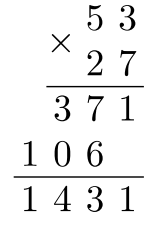
    clipboard_e55390c108993ead74561c60a31214d32.png

    Alternativamente, podemos usar área rectangular total para encontrar el producto\(53 \times 27\). El área total del área es la suma de cuatro áreas rectangulares más pequeñas.

    Paso 1: Escribe ambos\(53\) y\(27\) como la suma de decenas y unas:

    \(\begin{array}&&53 = 50 + 3\\ &27 = 20 + 7 \end{array}\)

    Paso 2: Cada longitud lateral del rectángulo más grande se divide en la suma de decenas y unas.

    Paso 3: Encuentra el área de cada uno de los cuatro rectángulos más pequeños.

    Paso 4: Suma las cuatro áreas para encontrar el área total.

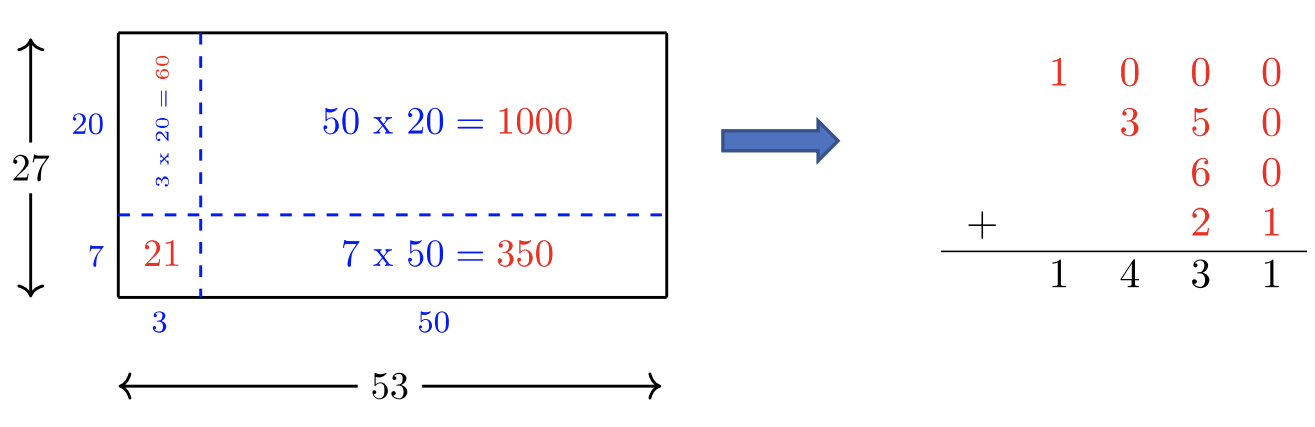
    clipboard_eb2dac278b5ef889b846be7a322fb80ba.png

    Por cualquiera de los dos métodos, la respuesta correcta es\(53 \times 27 = (50 + 3)(20 + 7) = 1431\).

    Sin embargo, el método de área rectangular nos informa cómo se multiplican correctamente los binomios. Podemos seguir un patrón de multiplicación llamado FOIL: F irst O uter I nner L ast.

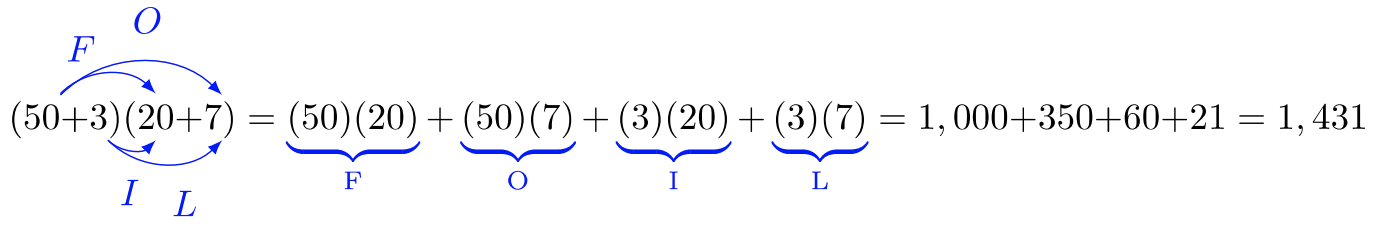
    clipboard_e583d6af916de22d5c96bd2d6c330edcd.png

    Los binomios que contienen expresiones algebraicas se comportarán del mismo modo que se comportan los números reales. Se requiere el método FOIL cuando las variables se sitúan en lugar de números reales.

    Ejemplo 1.2.1

    Multiplicar\((2x + 5)(3x + 2)\).

    Solución

    Utilice el método FOIL:

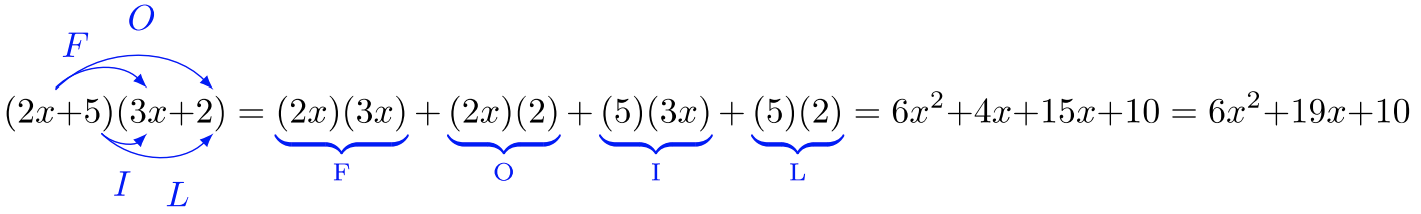
    clipboard_ed9513a55ff4b749682e9d63685df77dc.png

    Ejemplo 1.2.2

    Multiplicar\((2x − 5)(x − 4)\).

    Solución

    Utilice el método FOIL. La resta se puede cambiar por suma\((2x + (−5))(x + (−4))\), pero es costumbre permitir que la resta sea percibida como negativa en lugar de escribirla como tal. En definitiva, presta atención a tus valores negativos y ajusta la operación (suma o resta) en consecuencia.

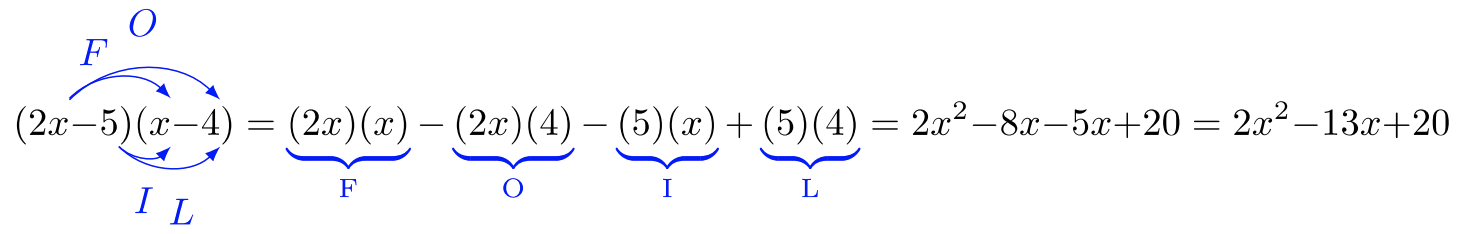
    clipboard_e97bab29a0f6ea4fecc5f6e375afc0008.png

    Productos Especiales de Binomios

    El método FOIL se puede utilizar de manera confiable para multiplicar todos los binomios. Es decir, no está obligado a utilizar los siguientes productos especiales si desea continuar usando FOIL. Sin embargo, acostumbrarse a observar patrones matemáticos y usar patrones es una buena habilidad matemática para perfeccionar.

    Caso 1: Los mismos términos, pero un binomio es una suma, mientras que el otro binomio es una diferencia.

    Ejemplo 1.2.3

    Multiplicar\((3x + 7)(3x − 7)\)

    Solución

    Por el método FOIL:\((3x + 7)(3x − 7) = 9x^2 − 21x + 21x − 49 = 9x^2 - 49\) Los dos términos intermedios cancelan.

    Caso 2: Los mismos términos, y la misma operación: o ambos son más, o ambos son menos.

    Ejemplo 1.2.4

    Multiplicar\((5x + 2)(5x + 2)\)

    Solución

    Por el método FOIL:\((5x + 2)(5x + 2) = 25x^2 + 10x + 10x + 4 = 25x^2 + 20x+ 4\) Los dos términos medios son iguales. ¡Doblar!

    Productos Especiales de Binomios

    \[(A+B)(A-B) = A^2 - B^2\]

    El producto se llama diferencia de cuadrados.

    \[(A+B)^2 = (A+B)(A+B) = A^2 + 2AB + B^2 \\ (A-B)^2 = (A-B)(A-B) = A^2 - 2AB + B^2\]

    El producto se llama trinomio cuadrado perfecto.

    Ejemplo 1.2.5

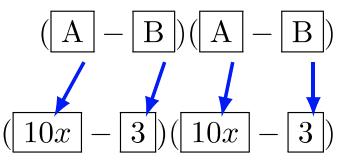
    Multiplicar\((10x − 3)^2\).

    Solución

    Utilice la fórmula especial del producto:\((A-B)^2 = (A-B)(A-B) = A^2 - 2AB + B^2\)

    Determinar los valores\(A\) y\(B\). La fórmula requerirá estas sustituciones:\(A = 10x \text{ and } B = 3\)

    clipboard_eb124014ae3b884dc0c0c04d49ddf6841.png

    \(\begin{array} &&A^2 - 2AB + B^2 &\text{Substitute \(A=10x\)y\(B=3\)}\\ & =( 10x) ^2 - 2 (10x) (3) + 3^2 &\\ &= 100x^2 - 60x + 9 &\ end {array}\)

    Contestar\((10x − 3)^2 = 100x^2 - 60x + 9\)

    Ejemplo 1.2.6

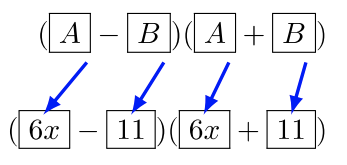
    Multiplicar\((6x − 11)(6x + 11)\)

    Solución

    Utilice la fórmula especial del producto:\((A-B)(A+B) = A^2 - B^2\)

    Determinar los valores\(A\) y\(B\). La fórmula requerirá estas sustituciones:\(A = 6x \text{ and } B = 11\)

    clipboard_e1f0eac5dc643a5a102444812b1fe11c1.png

    \(\begin{array} &&A^2 - B^2 &\text{Substitute \(A=6x\)y\(B=11\)}\\ & =( 6x) ^2 - 11^2 &\\ &= 36x^2 - 121 &\ end {array}\)

    Respuesta:\((6x − 11)(6x + 11) = 36x^2 - 121\)

    Ejemplo 1.2.7

    ¿Qué propiedad de multiplicación se demuestra en la siguiente ecuación?

    \((6x − 11)(6x + 11) = (6x + 11)(6x − 11)\)

    Solución

    Las cantidades\((6x − 11)\) y\((6x + 11)\) se colocan en el lugar de los números reales\(a\) y\(b\). El orden de multiplicación no arroja resultados diferentes. Es decir, para todos los números reales\(a\) y\(b\),\(ab = ba\). La ecuación demuestra la Propiedad Conmutativa de la Multiplicación.

    Multiplicar polinomios de más de 2 términos

    Por último, abordemos la multiplicación de polinomios de cualquier número de términos, no solo binomios. El método FOIL se desarrolló utilizando el área de un rectángulo. Utilizaremos el mismo método para desarrollar una estrategia para multiplicar polinomios de más de\(2\) términos entre sí.

    Ejemplo 1.2.8

    Multiplicar\((2x^2 − 4x + 5)(x^2 + 6x − 8)\)

    Solución

    El concepto de área de un rectángulo será nuestra guía 1.

    \(\underbrace{(2x^2 - 4x + 5)}_{\text{Length}} \;\underbrace{(x^2 + 6x - 8)}_{\text{Width}} = \text{ Total Area}\)

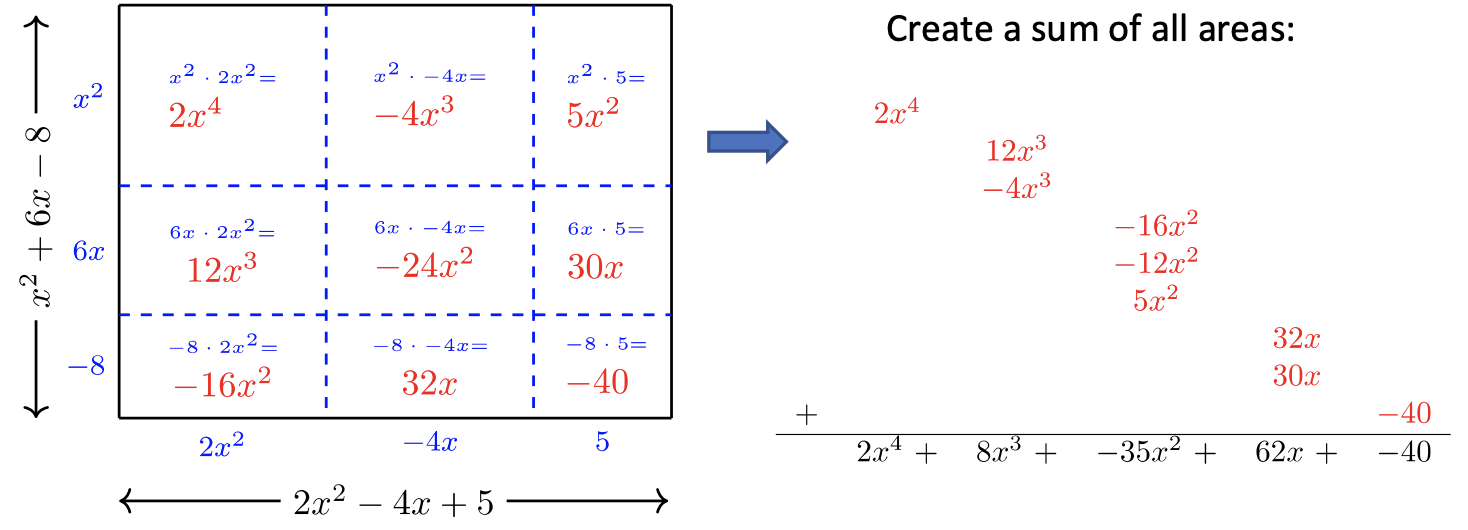
    clipboard_e286323f9c65834edbc15c7e41dc44dbb.png

    Respuesta:\((2x^2 − 4x + 5)(x^2 + 6x − 8) = 2x^4 + 8x^3 -35x^2 +62x -40\)

    Ejemplo 1.2.9

    Multiplicar\(2x(x^3 − 5)(x^2 − 7x + 10)\)

    Solución

    Tenemos\(3\) cantidades,\(2x\),\(x^3 − 5\), y\(x^2 − 7x + 10\). Estas cantidades se sitúan en el lugar de los números reales. Si se multiplicaran tres números reales, por ejemplo:\(3 \cdot 4 \cdot 7\), ¿cómo lo harías? ¡Selecciona dos números cualesquiera para multiplicar! \((3 \cdot 4)^7 = 12 \cdot 7 = 84\). Asimismo, el álgebra sigue las mismas reglas.

    \(\begin{array} &&[2x(x^3 − 5)](x^2 − 7x + 10) &\text{Multiply two quantities together.} \\ &(2x^4 − 10x)(x^2 − 7x + 10) &\text{Use the distributive property to multiply.} \end{array}\)

    Crea una tabla con los términos de cada polinomio representando el largo y ancho de un rectángulo:

    \(x^2\) \(-7x\) \(10\)
    \(2x^4\) \ (x^2\) ">\(2x^6\) \ (-7x\) ">\(-14x^5\) \ (10\) ">\(20x^4\)
    \(-10x\) \ (x^2\) ">\(-10x^3\) \ (-7x\) ">\(70x^2\) \ (10\) ">\(-100x\\)

    Contestar\(2x(x^3 − 5)(x^2 − 7x + 10) = 2x^6 - 14x^5 +20x^4 -10x^3 +70x^2 -100x\)

    ¡Pruébalo! (Ejercicios)

    Para #1 -12, multiplica usando el método FOIL.

    1. \((x + 7)(x + 6)\)
    2. \((y + 5)(y + 3)\)
    3. \((2t + 9)(t + 1)\)
    4. \((n − 2)(n + 4)\)
    5. \((p + 8)(p− 11)\)
    6. \((3q − 1)(2q + 1)\)
    7. \((10 − m)(12 − m)\)
    8. \((15 − w)(2 + w)\)
    9. \((9 + u)(2 − u)\)
    10. \((5z + 12)(z − 1)\)
    11. \((3r + 7)(2r − 7)\)
    12. \((6n + 5)(6n − 4)\)

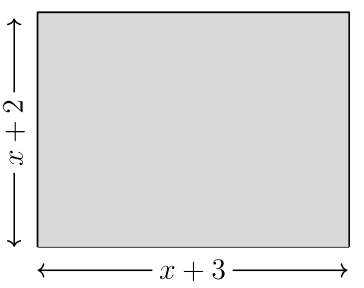
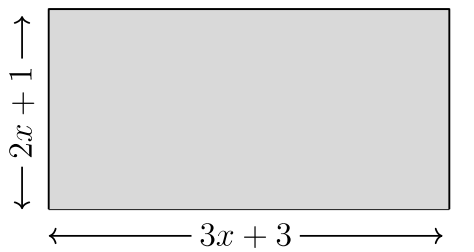
    Para #13 -14, encuentra el polinomio que representa el área de cada rectángulo.

    13. clipboard_e82d14c7075079b25a78a177da5280272.png

    14. clipboard_efc41a433f360f90f66fb741bd99c1e4b.png

    Para #15 -23, use una Fórmula de Productos Especiales apropiada para multiplicar.

    1. \((y + 5)^2\)
    2. \((p − 3)(p + 3)\)
    3. \((t − 7)^2\)
    4. \((7q − 1)(7q + 1)\)
    5. \((4n + 9)^2\)
    6. \((8c + 6)(8c − 6)\)
    7. \((2u − 2)^2\)
    8. \((4 − z)^2\)
    9. \((5 − 3r)^2\)

    Para #24 -31, multiplicar los polinomios.

    1. \((x − 8)(x^2 − 3x + 1)\)
    2. \((2y + 3)(y^2 − 6y − 4)\)
    3. \((u^2 + 1)(u^2 + 2u − 5)\)
    4. \((4p^2 − p + 2)(p^2 + 2p − 3)\)
    5. \(2h(3h − 1)(6h + 1)\)
    6. \(5t(t − 4)(t^2 + 3t − 2)\)
    7. \((2n + 1)^3\)
    8. \(4b(b − 3)^2\)

    This page titled 1.2: Método FOIL y Productos Especiales is shared under a CC BY-SA 4.0 license and was authored, remixed, and/or curated by Jennifer Freidenreich.