3.1: Transformaciones de f (x)
- Page ID
- 115914
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
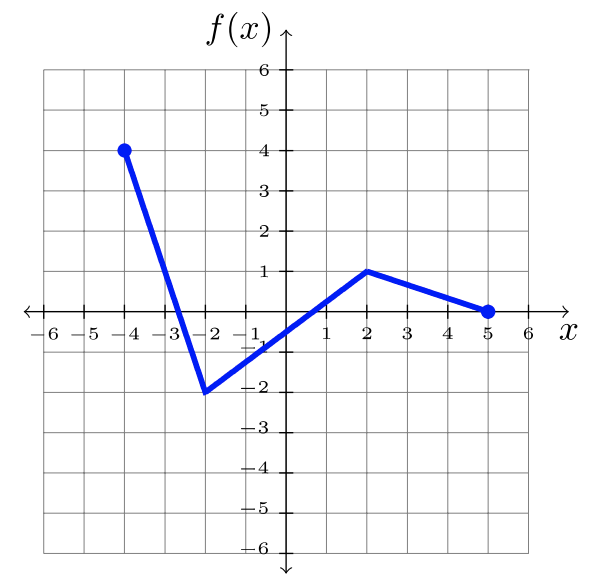
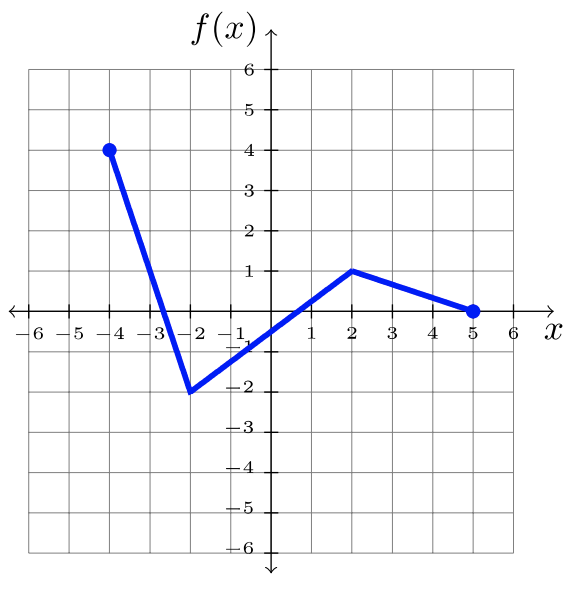
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En esta sección, practicarás la manipulación de una gráfica dada, de acuerdo con la notación de función correspondiente. Usaremos la función\(f\), graficada a continuación, para demostraciones a lo largo de esta sección. ¡Pero cualquier gráfica servirá!
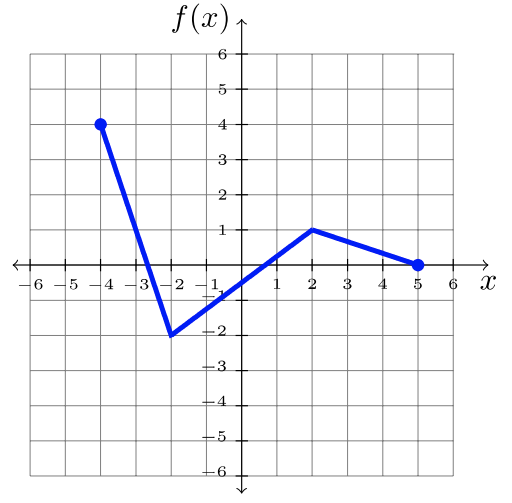
Al final de esta sección, aprenderás a leer la notación de funciones como un blueprint, reposicionar la gráfica de acuerdo con las instrucciones que da. Aprenderás a aplicar estas transformaciones.
| Transformación | Notación de funciones\((c > 0)\) | Notas |
|---|---|---|
| \(c\)Unidades de cambio hacia arriba | \ ((c “> 0)\)" >\(0>y = f(x) + c\) | Si la suma o resta está fuera de la función, cambie hacia arriba o hacia abajo. |
| \(c\)Unidades de cambio hacia abajo | \ ((c “> 0)\)" >\(0>y = f(x) − c\) | |
| \(c\)Unidades de cambio a la derecha | \ ((c “> 0)\)" >\(0>y = f(x-c)\) | Si la suma o resta está dentro de la función, desplace a la izquierda o a la derecha. |
| \(c\)Unidades de cambio a la izquierda | \ ((c “> 0)\)" >\(0>y = f(x+c)\) | |
| Reflexión a través del\(x\) eje | \ ((c “> 0)\)" >\(0>y = -f(x)\) | Si el negativo está fuera de la función, hay una reflexión\(x\) -axis. |
| Reflexión a través del\(y\) eje | \ ((c “> 0)\)" >\(0>y=f(-x)\) | Si el negativo está dentro de la función, hay una reflexión\(y\) -axis. |
| Cambio de escala vertical | \ ((c “> 0)\)" >\(0>y=cf(x)\) | Si el multiplicador,\(c\), está fuera de la función, hay un cambio de escala vertical. |
| Cambio de escala horizontal | \ ((c “> 0)\)" >\(0>y=f(cx)\) | Si el multiplicador,\(c\), está dentro de la función, hay un cambio de escala horizontal. |
Los ejemplos demuestran la manipulación apropiada a la gráfica de\(f\). La gráfica original\(f\) se conoce como la gráfica padre. El concepto se puede aplicar a cualquier función, pero se usa la misma función padre en cada ejemplo a continuación.
Usando la gráfica de\(f\), transforma la gráfica de manera apropiada.
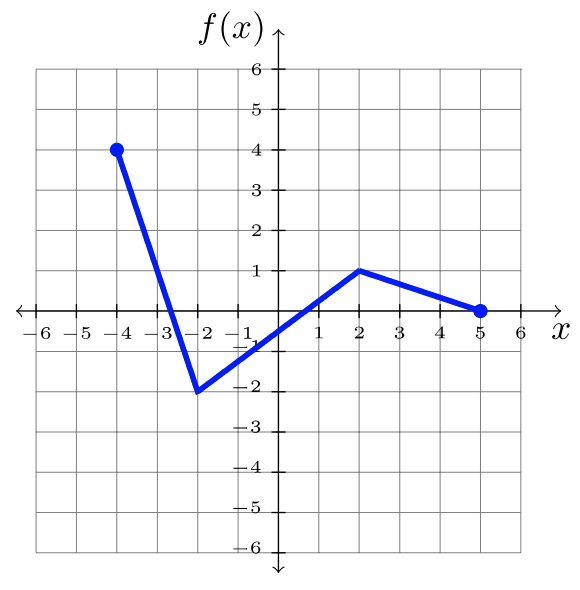
- \(y = f(x + 2)\)
- \(y = f(x) + 2\)
- \(y = f(x − 2)\)
Solución
- Paso 1: Identificar la transformación en la gráfica padre,\(f\).
\(\begin{array}&&y = f(x +2) &\text{Plus \(2\)Función interior; Mayús a la izquierda\(2\)}\ end {array}\)
Paso 2: Desplazar cada\(2\) unidad de punto a la izquierda:
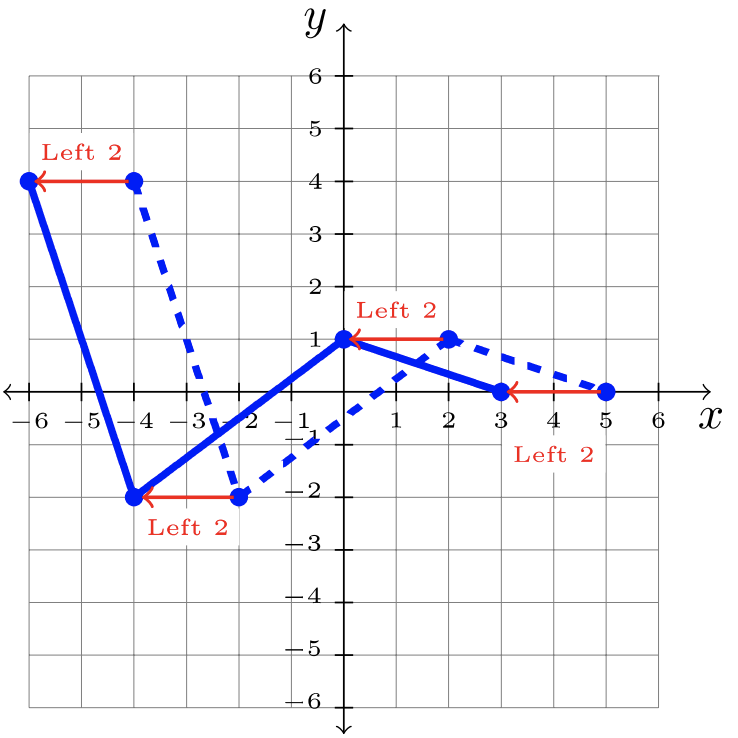
Paso 3: Respuesta:\(y = f(x + 2)\)
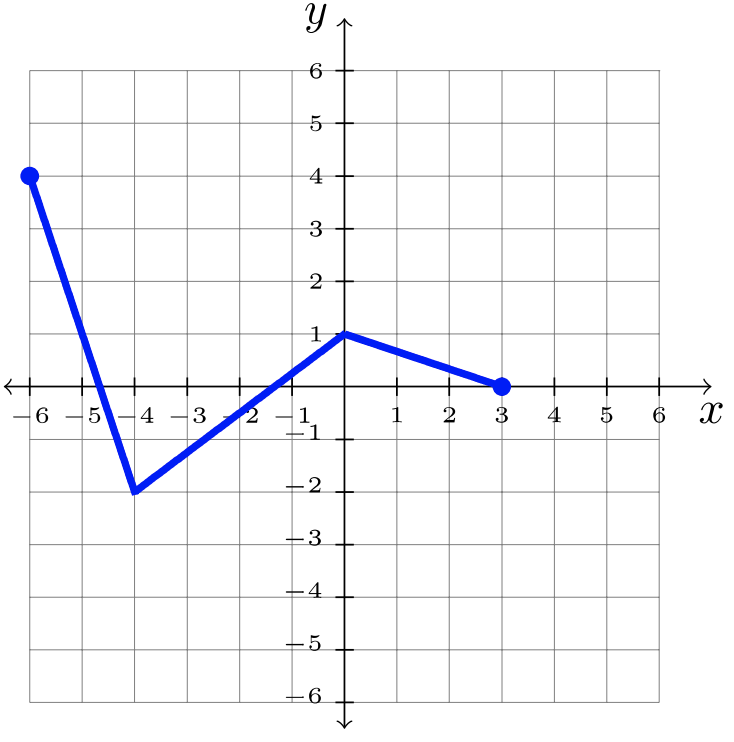
- Paso 1: Identificar la transformación en la gráfica padre,\(f\).
\(\begin{array}&&y = f(x) +2 &\text{Plus \(2\)Función exterior; Mayús hacia arriba\(2\)}\ end {array}\)
Paso 2: Desplazar cada\(2\) unidad de punto hacia arriba:
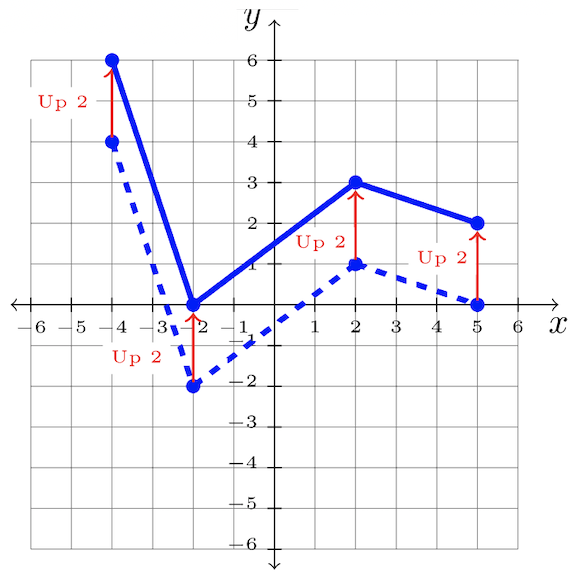
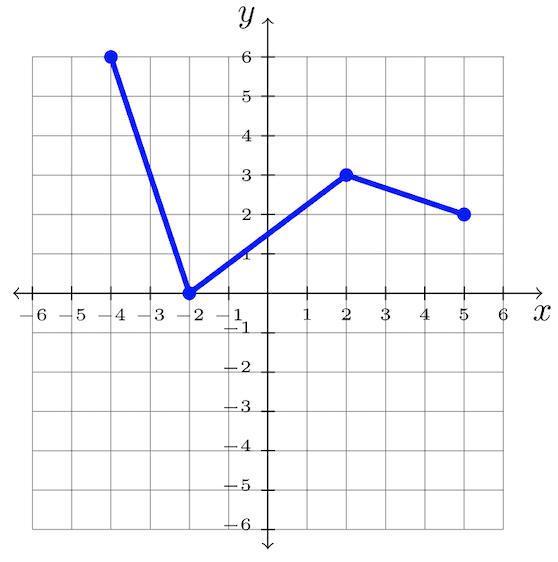
Paso 3: Respuesta:\(y = f(x )+ 2\)
- Paso 1: Identificar la transformación en la gráfica padre,\(f\).
\(\begin{array}&&y = f(x -2) &\text{Minus \(2\)Función interior; Mayús a la derecha\(2\)}\ end {array}\)
Paso 2: Desplazar cada\(2\) unidad de punto a la derecha:
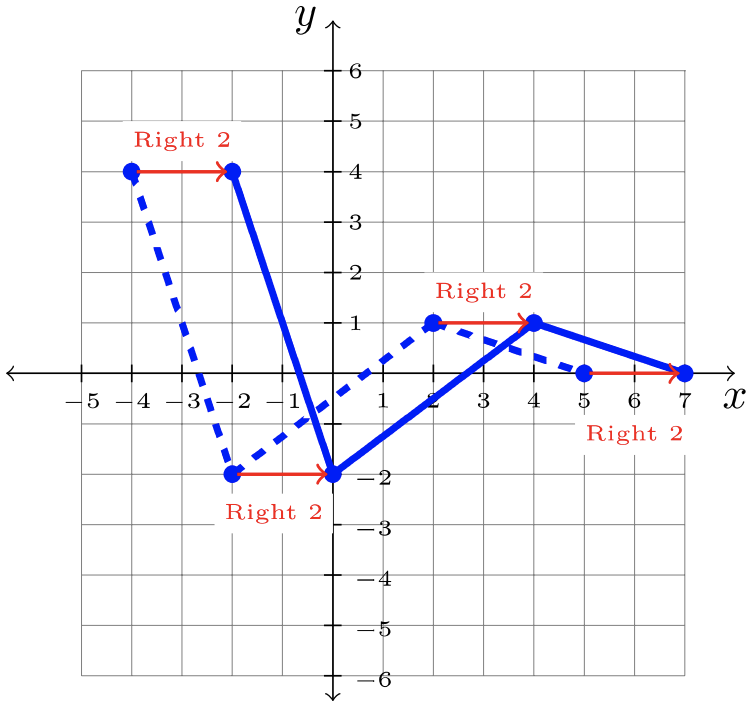
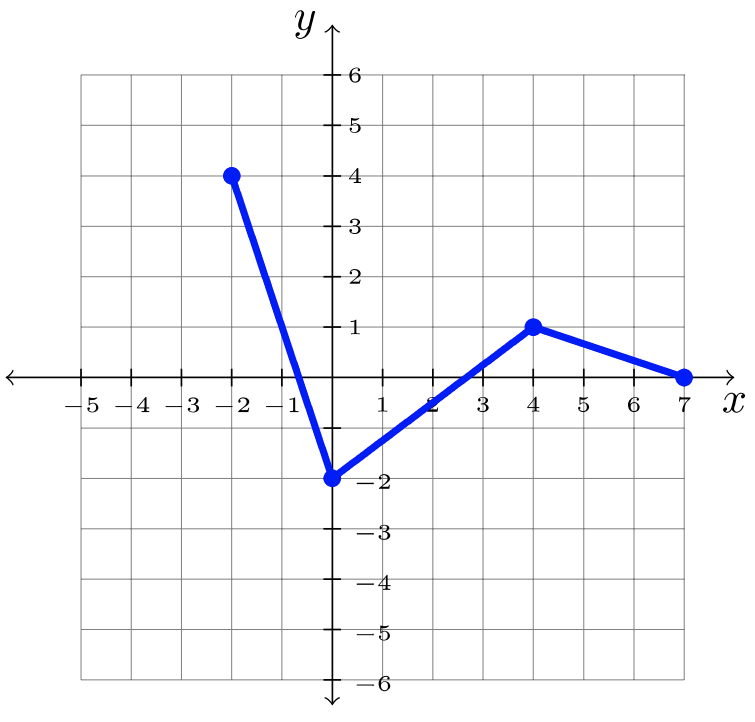
Paso 3: Respuesta:\(y = f(x -2)\)
Usando la gráfica de\(f\), transforma la gráfica de manera apropiada.
- \(y = f(x) − 2\)
- \(y = −f(x)\)
- \(y = f(−x)\)
Solución
- Paso 1: Identificar la transformación en la gráfica padre,\(f\).
\(\begin{array}&&y = f(x) -2 &\text{Minus \(2\)Función exterior; Mayús hacia abajo\(2\)}\ end {array}\)
Paso 2: Desplazar cada\(2\) unidad de punto hacia abajo:
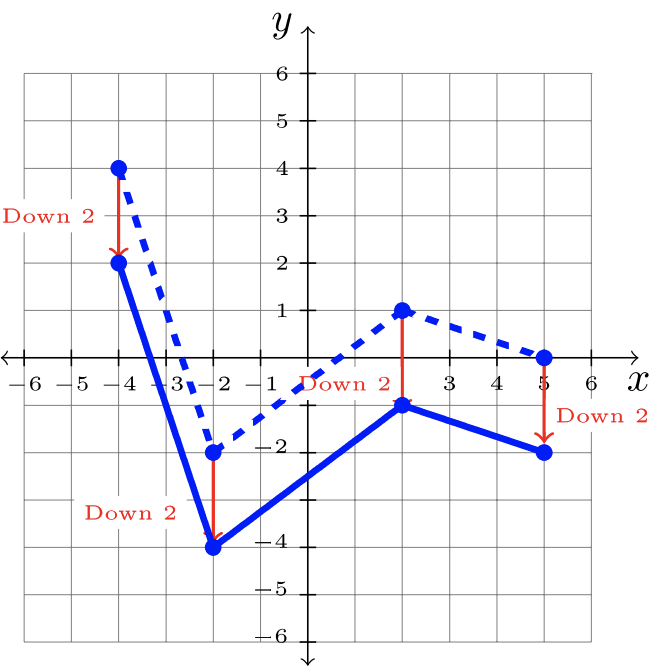
Paso 3: Respuesta:\(y = f(x) -2\)
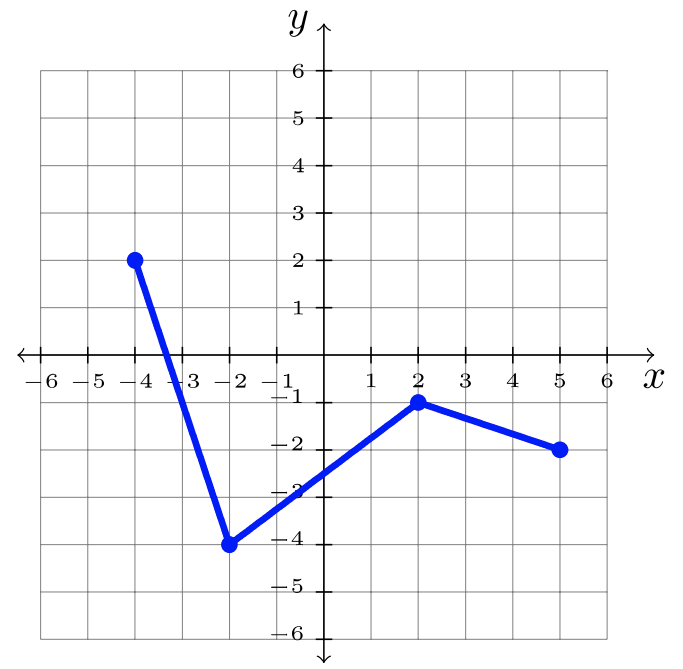
- Paso 1: Identificar la transformación en la gráfica padre,\(f\).
\(\begin{array}&&y = -f(x) &\text{Negative Outside Function; \(x\)-eje Reflejo}\ end {array}\)
Paso 2: Cambiar cada\(y\) -valor a su opuesto.
Paso 3: Respuesta:\(y = −f(x)\)
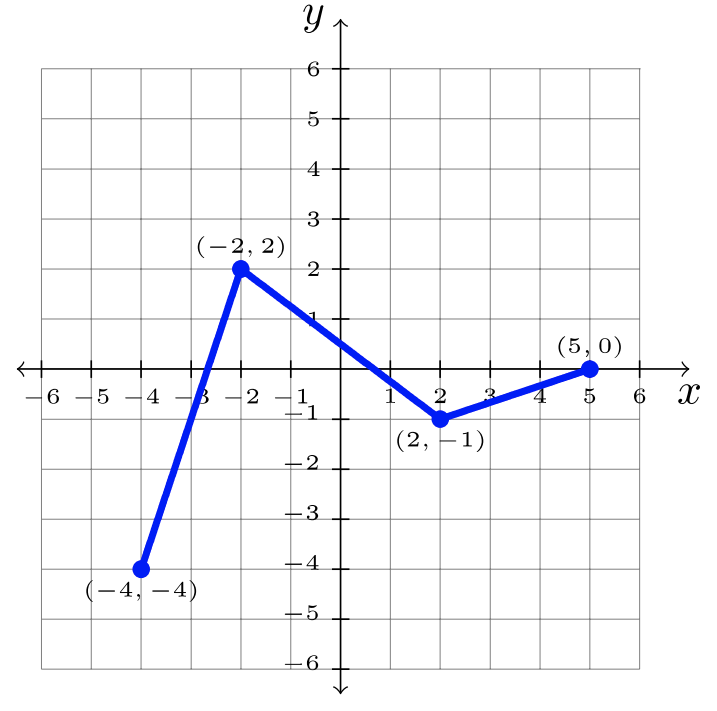
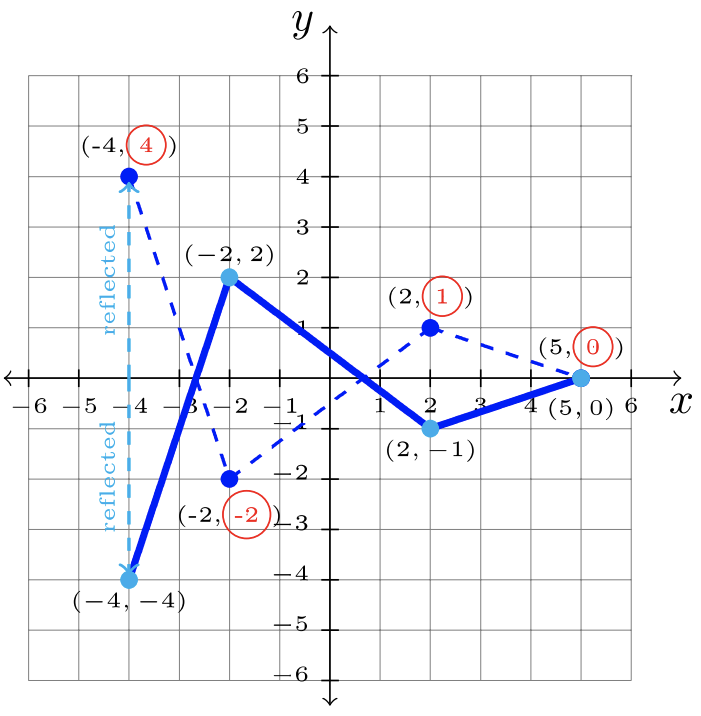
- Paso 1: Identificar la transformación en la gráfica padre,\(f\).
\(\begin{array}&&y = f(-x) &\text{Negative Inside Function; \(y\)-eje Reflejo}\ end {array}\)
Paso 2: Cambiar cada\(x\) -valor a su opuesto.
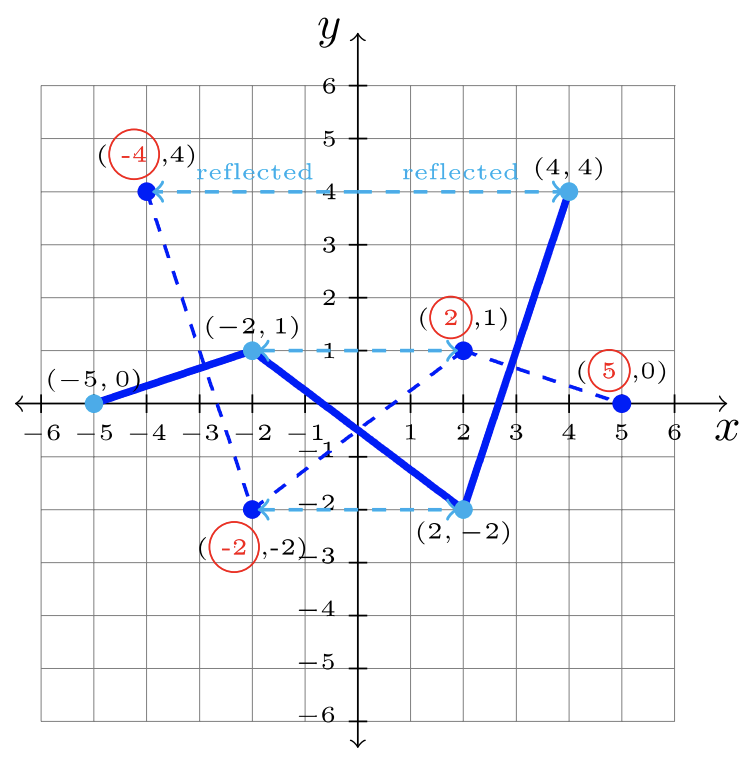
Paso 3: Respuesta:\(y = f(x) -2\):
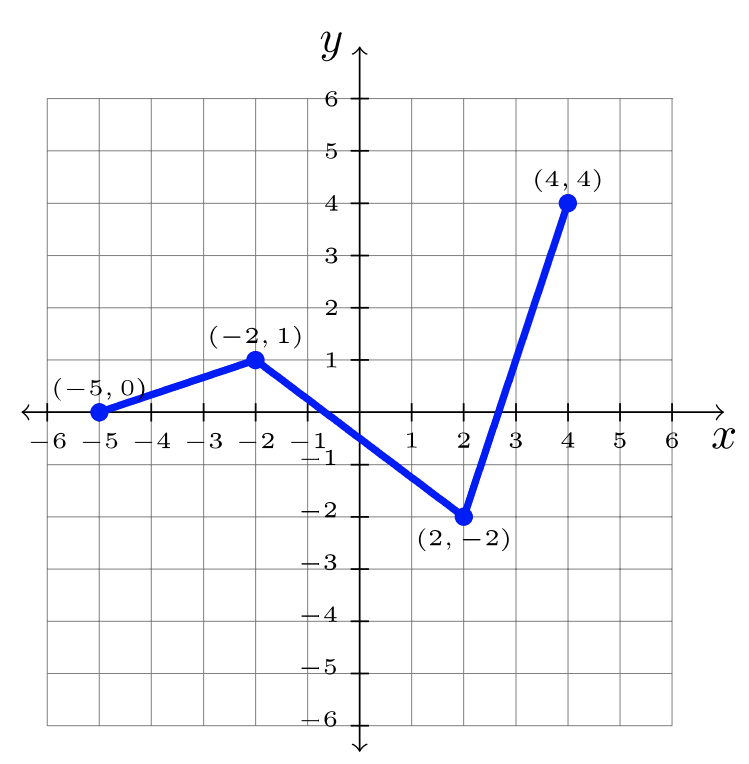
Usando la gráfica de\(f\), transforma la gráfica de manera apropiada.
- \(y = 2f(x)\)
- \(y = f(2x)\)
Solución
- Paso 1: Identificar la transformación en la gráfica padre,\(f\).
\(\begin{array}&&y = 2f(x) &\text{Times \(2\)Función exterior; Cambio de escala vertical\(2\)}\ end {array}\)
Paso 2: Multiplica cada\(y\) -valor por\(2\).
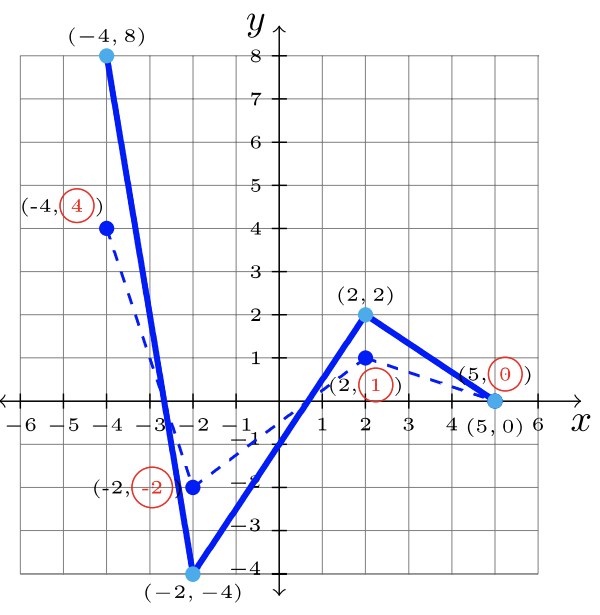
Paso 3: Respuesta:\(y = 2f(x)\):
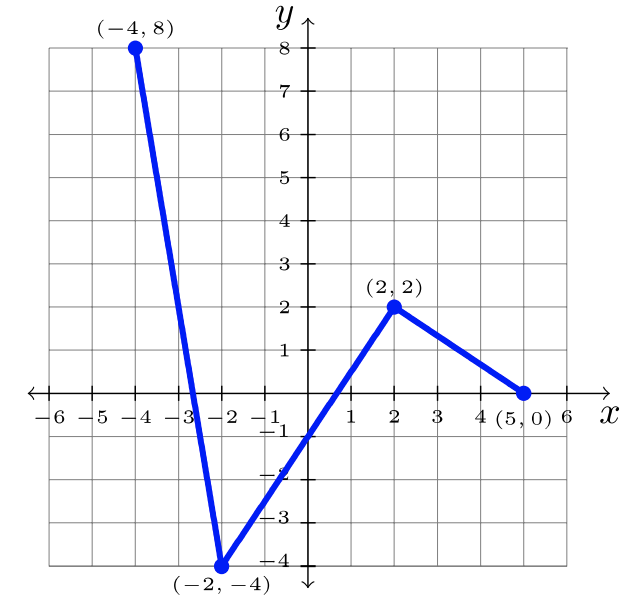
Precaución: ¡El cambio de escala horizontal es contraintuitivo! Para\(y = f(cx)\), la gráfica de\(f\) se escala horizontalmente por un factor de\(\dfrac{1}{c}\). En otras palabras, si\(c > 1\), entonces la gráfica se comprime. Si\(0 < c < 1\), (una fracción apropiada) entonces la gráfica se estira horizontalmente
- Paso 1: Identificar la transformación en la gráfica padre,\(f\).
\(\begin{array}&&y =- f(x) &\text{Minus \(2\)Función exterior; Mayús hacia abajo\(2\)}\ end {array}\)
Paso 2: Multiplica cada\(x\) -valor por\(\dfrac{1}{2}\).
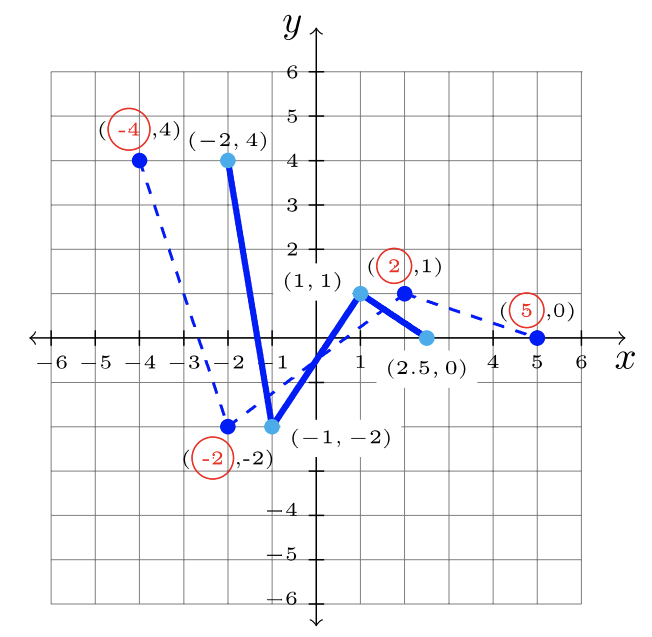
Paso 3: Respuesta:\(y = f(2x)\):
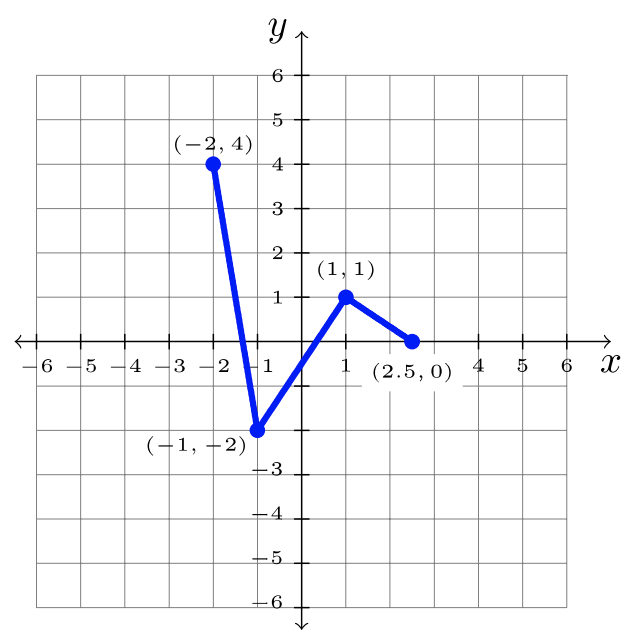
Combinando Transformaciones
En muchos casos, graficar una función requerirá más de una transformación. Realizar transformaciones en el mismo orden que PEMDAS, el orden de las operaciones. El siguiente ejemplo demuestra la manipulación de una gráfica mediante múltiples transformaciones.
Usando la gráfica de\(f\),
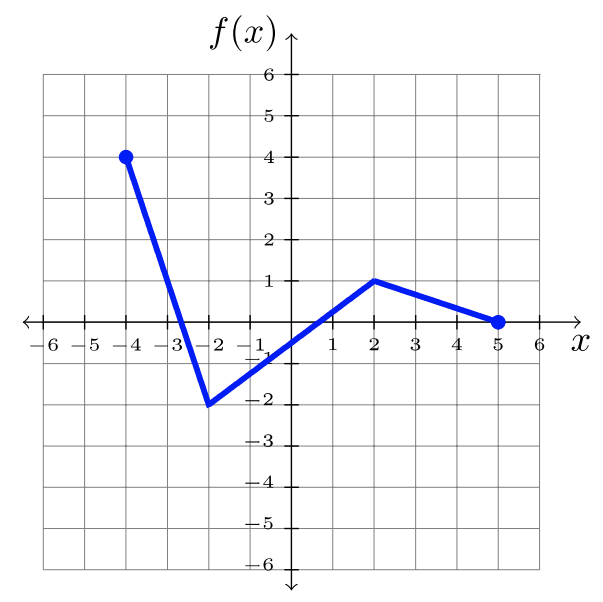
Esbozar la gráfica:\(y = −2f(x − 1) − 3\)
Solución
Dado que las transformaciones se van a realizar en el orden de PEMDAS, cada transformación se anota entonces ordenada.
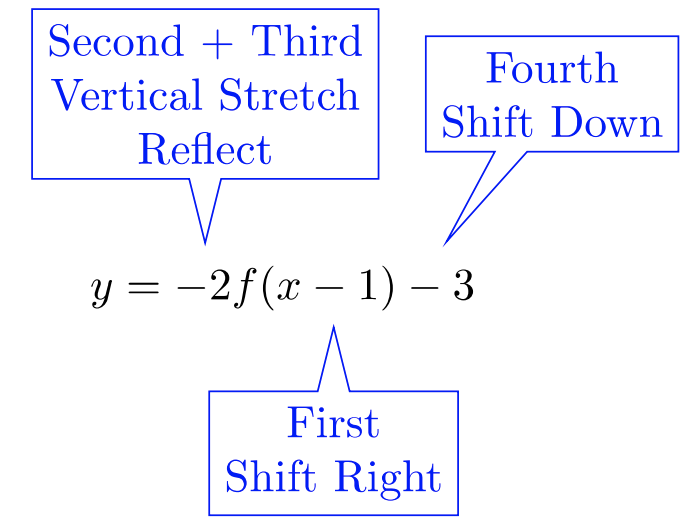
Las transformaciones de\(4\) puntos de\(f\) se trazan a continuación. Después de completar todas las transformaciones, graficar los puntos transformados establecidos en la columna final. Conecta los puntos para crear la gráfica.
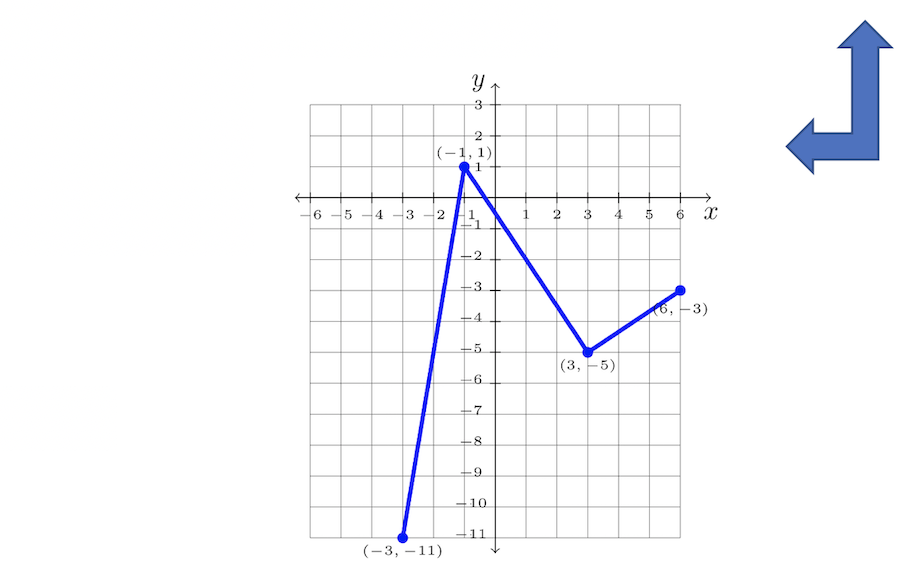
| \(f\)Punto | Mayús a la derecha: Agrega uno a cada\(x\) valor. | Estirar y reflejar verticales: Multiplicar\(y\) -valores por\(−2\). | Desplazamiento hacia abajo: restar\(3\)\(y\) de cada valor |
|---|---|---|---|
| Punto de\ (f\)” >\((−4, 4)\) | \ (x\) -valor.” >\((−3, 4)\) | \ (y\) -valores por\(−2\).” >\((−3, −8)\) | \ (3\) de cada\(y\) -valor">\((−3, −11)\) |
| Punto de\ (f\)” >\((−2, −2)\) | \ (x\) -valor.” >\((−1, −2)\) | \ (y\) -valores por\(−2\).” >\((−1, 4)\) | \ (3\) de cada\(y\) -valor">\((−1, 1)\) |
| Punto de\ (f\)” >\( (2, 1)\) | \ (x\) -valor.” >\((3, 1)\) | \ (y\) -valores por\(−2\).” >\((3, −2)\) | \ (3\) de cada\(y\) -valor">\((3,-5)\) |
| Punto de\ (f\)” >\((5, 0)\) | \ (x\) -valor.” >\((6, 0)\) | \ (y\) -valores por\(−2\).” >\((6, 0)\) | \ (3\) de cada\(y\) -valor">\((6,-3)\) |
La gráfica\(y = −2f(x − 1) − 3\) se muestra a continuación:
¡Pruébalo! (Ejercicios)
Para los ejercicios 1-17, use la gráfica de\(f\) a la derecha, junto con la (s) transformación (es) apropiada (s), para esbozar la función transformada. Usa papel gráfico.
- \(y = −f(x)\)
- \(y = f(x) + 1\)
- \(y = f(x + 2)\)
- \(y = f(x − 3)\)
- \(y = f(x) − 4\)
- \(y = f(−x)\)
- \(y = 3f(x)\)
- \(y = f(2x)\)
- \(y = \dfrac{1}{2} f(x)\)
- \(y = f \left( \dfrac{1}{2} x \right)\)
- \(y = −f(x)\)
- \(y = 2f(x + 1)\)
- \(y = 4 + f(x − 2)\)
- \(y = 3 − f(x)\)
- \(y = f(x − 3) − 3\)
- \(y = −3f \left( \dfrac{1}{3} x \right)\)
- \(y = 2f(−x) − 1\)
Para #18 -24, escriba la función que correspondería a las transformaciones descritas en\(f\).
- Refleja\(f\) a través del\(y\) eje, luego mueve la gráfica hacia arriba\(5\) unidades.
- Estirar\(f\) verticalmente por un factor de\(6\), luego desplazar las\(8\) unidades gráficas a la izquierda.
- Desplace la gráfica\(f\) a las\(10\) unidades de la derecha, luego desplace la gráfica hacia abajo\(7\) unidades.
- Reflejar\(f\) a través del\(x\) eje -eje, mover las\(3\) unidades de la gráfica hacia la derecha, luego desplazar la gráfica hacia arriba\(12\) unidades
- Reflejar\(f\) a través del\(x\) eje, estirarlo verticalmente por un factor de\(4\), luego desplazarlo hacia abajo\(5\) unidades.
- Reflejar\(f\) a través del\(y\) eje -eje, desplazarlo hacia la izquierda (9\) unidades, luego desplazarlo hacia arriba\(8\) unidades.
- Comprimir\(f\) horizontalmente por un factor de\(\dfrac{1}{4}\), reflejarlo a través del\(x\) eje, luego desplazar hacia abajo\(1\) la unidad.


