4.1: Funciones exponenciales

La India es el segundo país más poblado del mundo, con una población en 2008 de alrededor de 1.140 millones de personas. La población crece alrededor de 1.34% cada año (Banco Mundial, Indicadores de Desarrollo Mundial, como se informó en http://www.google.com/publicdata, recuperado el 20 de agosto de 2010). Podríamos preguntarnos si podemos encontrar una fórmula para modelar a la población\(P\),, en función del tiempo\(t\), en años posteriores a 2008, si la población sigue creciendo a este ritmo.

En el crecimiento lineal, tuvimos una tasa constante de cambio —una constante\(number\) que la producción aumentaba por cada incremento en la entrada. Por ejemplo, en la ecuación\(f(x)=3x+4\), la pendiente nos dice que la salida aumenta en tres cada vez que la entrada aumenta en uno. Este escenario poblacional es diferente —tenemos una\(percent\) tasa de cambio en lugar de un número constante de personas como nuestra tasa de cambio.

Para ver la significación de esta diferencia considera estas dos empresas:

• La compañía\(A\) cuenta con 100 tiendas, y se expande abriendo 50 nuevas tiendas al año
• La compañía\(B\) cuenta con 100 tiendas, y se expande al aumentar el número de tiendas en un 50% de su total cada año.

Mirando algunos años de crecimiento para estas empresas:

Año	Tiendas, empresa\(A\)		Tiendas, empresa\(B\)
0	\ (A\)” style="vertical-align:middle; ">100	Comenzando con 100 cada uno	\ (B\)” style="vertical-align:middle; ">100
1	\ (A\)” style="vertical-align:middle; ">100 + 50 = 150	Ambos crecen en 50 tiendas en el primer año.	\ (B\)” style="vertical-align:middle; ">100 + 50% de 100 100 + 0.50 (100) = 150
2	\ (A\)” style="vertical-align:middle; ">150 + 50 = 200	La tienda A crece por 50, la tienda B crece 75	\ (B\)” style="vertical-align:middle; ">150 + 50% de 150 150 + 0.50 (150) = 225
3	\ (A\)” style="vertical-align:middle; ">200 + 50 = 250	La tienda A crece por 50, la tienda B crece en 112.5	\ (B\)” style="vertical-align:middle; ">225 + 50% de 225 225 + 0.50 (225) = 337.5

Observe que con el crecimiento porcentual, cada año la compañía crece 50% del total del año en curso, por lo que a medida que la compañía crece, también crece el número de tiendas agregadas en un año.

Para tratar de simplificar los cálculos, observe que después de 1 año el número de tiendas para compañía\(B\) fue:

\[100+0.50\nonumber\]o equivalentemente factorizando
\[100(1+0.50)=150\nonumber\]

Podemos pensar en esto como “el nuevo número de tiendas es el 100% original más otro 50%”.

Después de 2 años, el número de tiendas fue:

\[150+0.50\nonumber\]o equivalentemente factorizando
\[150(1+0.50)\nonumber\] ahora recordar el 150 vino de 100 (1+0.50). Sustituyendo eso,
\[100(1 + 0.50) (1 + 0.50) = 100(1 + 0.50)^2 = 225\nonumber\]

Después de 3 años, el número de tiendas fue:

\[225+0.50\nonumber\]o equivalentemente factorizando
\[225(1+0.50)\nonumber\] ahora recordar el 225 vino de\(100(1+0.50)^{2}\). Sustituyendo eso,
\[100(1 + 0.50)^2 (1 + 0.50) = 100(1 + 0.50)^3 = 225\nonumber\]

A partir de esto, podemos generalizar, notando que para mostrar un incremento del 50%, cada año multiplicamos por un factor de (1+0.50), así que después de\(n\) años, nuestra ecuación sería

\[B(n)=100(1+0.50)^{n}\nonumber\]

En esta ecuación, el 100 representó la cantidad inicial, y el 0.50 fue la tasa de crecimiento porcentual. Generalizando aún más, llegamos a la forma general de funciones exponenciales.

Definición: Función exponencial

Una función de crecimiento o decaimiento exponencial es una función que crece o se contrae a una tasa de crecimiento porcentual constante. La ecuación se puede escribir en la forma

\[f(x)=a(1+r)^{x} \nonumber\]

o

\[f(x)=ab^{x} \nonumber\]

dónde\(b = 1+r\) y

• \(a\)es el valor inicial o inicial de la función
• \(r\)es el porcentaje de crecimiento o tasa de decaimiento, escrito como decimal
• \(b\)es el factor de crecimiento o multiplicador de crecimiento. Dado que los poderes de los números negativos se comportan de manera extraña, limitamos\(b\) a valores positivos.

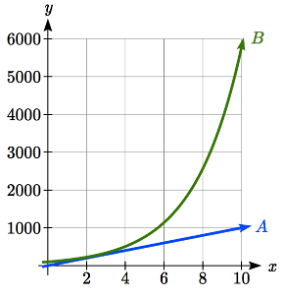
Para ver más claramente la diferencia entre crecimiento exponencial y lineal, compare las dos tablas y gráficas a continuación, que ilustran el crecimiento de la empresa\(A\) y\(B\) se describen anteriormente a lo largo de un marco de tiempo más largo si los patrones de crecimiento continuaran.

\ (\ begin {array} {|r|r|r|}
\ hline\ texto {años} &\ texto {Compañía} A &\ texto {Compañía} B
\\\ hline 2 & 200 & 225
\\ hline 4 & 300 & 506\
\ hline 6 & 400 & 1139\
\ hline 8 & 500 & 2563\\
\ hline 10 & 600 & 5767\\
\ hline
\ end {array}\)

Ejemplo\(\PageIndex{1}\)

Escriba una función exponencial para la población de la India, y utilícela para predecir la población en 2020.

Solución

Al inicio del capítulo nos dieron la población de la India de 1.140 millones de habitantes en el año 2008 y una tasa de crecimiento porcentual de 1.34%. Usando 2008 como nuestra hora de inicio (\(t\)= 0), nuestra población inicial será de 1.140 millones. Dado que la tasa de crecimiento porcentual fue de 1.34%, nuestro valor para\(r\) es de 0.0134.

Usando la fórmula básica para el crecimiento exponencial\(f(x)=a(1+r)^{x}\) podemos escribir la fórmula,\(f(t)=1.14(1+0.0134)^{t}\)

Para estimar la población en 2020, evaluamos la función a\(t\) = 12, ya que 2020 es 12 años después de 2008.

\[f=1.14(1+0.0134)^{12} \approx 1.337\text{ billion people in 2020}\nonumber \]

Ejercicio\(\PageIndex{1}\)

Dados los tres enunciados a continuación, identificar cuáles representan funciones exponenciales.

1. El subsidio por costo de vida de los empleados estatales incrementa los salarios en 3.1% cada año.
2. Los empleados estatales pueden esperar un aumento de $300 cada año que trabajan para el estado.
3. Los costos de colegiatura han aumentado 2.8% cada año durante los últimos 3 años.

Contestar

a & c son funciones exponenciales, crecen en un% no un número constante.

Ejemplo\(\PageIndex{2}\)

Un certificado de depósito (CD) es un tipo de cuenta de ahorro que ofrecen los bancos, que suelen ofrecer una tasa de interés más alta a cambio de un período de tiempo fijo que dejará su dinero invertido. Si un banco ofrece un CD de 24 meses con una tasa de interés anual de 1.2% compuesta mensualmente, ¿a cuánto crecerá una inversión de $1000 a lo largo de esos 24 meses?

Solución

Primero, debemos notar que la tasa de interés es una tasa anual, pero se compone mensualmente, es decir, el interés se calcula y se agrega a la cuenta mensualmente. Para encontrar la tasa de interés mensual, dividimos la tasa anual de 1.2% por 12 ya que hay 12 meses en un año: 1.2% /12 = 0.1%. Cada mes ganaremos 0.1% de interés. A partir de esto, podemos establecer una función exponencial, con nuestro monto inicial de $1000 y una tasa de crecimiento de\(r\) = 0.001, y nuestro input\(m\) medido en meses.

\[f(m)=1000\left(1+\dfrac{.012}{12} \right)^{m}\nonumber\]
\[f(m)=1000(1+0.001)^{m}\nonumber\]

Después de 24 meses, la cuenta habrá crecido a\(f(24)=1000(1+0.001)^{24} =\$ 1024.28\)

Ejercicio\(\PageIndex{2}\)

Al observar estas dos ecuaciones que representan el saldo en dos cuentas de ahorro diferentes, ¿qué cuenta está creciendo más rápido y qué cuenta tendrá un saldo mayor después de 3 años?

• \(A(t)=1000\left(1.05\right)^{t}\)
• \(B(t)=900\left(1.075\right)^{t}\)

Contestar

\(B(t)\)está creciendo más rápido (\(r\)= 0.075 > 0.05), pero después de 3 años A (t) aún tiene un saldo de cuenta más alto

En todos los ejemplos anteriores, vimos un crecimiento exponencial. Las funciones exponenciales también se pueden usar para modelar cantidades que están disminuyendo a una tasa porcentual constante. Un ejemplo de ello es la desintegración radiactiva, un proceso en el que los isótopos radiactivos de ciertos átomos se transforman en un átomo de otro tipo, provocando una disminución porcentual del material original a lo largo del tiempo.

Ejemplo\(\PageIndex{3}\)

El bismuto-210 es un isótopo que decae radiactivamente en aproximadamente 13% cada día, lo que significa que 13% del resto de bismuto-210 se transforma en otro átomo (polonio-210 en este caso) cada día. Si comienzas con 100 mg de bismuto-210, ¿cuánto queda después de una semana?

Solución

Con la desintegración radiactiva, en lugar de que la cantidad aumente a una tasa porcentual, la cantidad está disminuyendo a una tasa porcentual. Nuestra cantidad inicial es\(a\) = 100 mg, y nuestra tasa de crecimiento será negativa 13%, ya que estamos disminuyendo:\(r\) = -0.13. Esto da la ecuación:

\[Q(d)=100(1-0.13)^{d} =100(0.87)^{d}\nonumber\]

Esto también puede explicarse al reconocer que si el 13% decae, entonces queda 87%.

Después de una semana, 7 días, la cantidad restante sería

\[Q(7)=100(0.87)^{7} =37.73\text{ mg of Bismuth-210 remains.}\nonumber \]

Ejercicio\(\PageIndex{3}\)

Una población de 1000 está disminuyendo 3% cada año. Encuentra la población en 30 años.

Contestar

\[P(t)=1000(1-0.03)^{t} =1000(0.97)^{t} \nonumber\]

\[P(30)=1000(0.97)^{30} =401.0071 \nonumber\]

Ejemplo\(\PageIndex{4}\)

\(T(q)\)representa el número total de contratos de teléfonos inteligentes Android, en miles, en poder de cierta región de tiendas de Verizon medidos trimestralmente desde el 1 de enero de 2016, interpretan todas las partes de la ecuación\(T(2)=86(1.64)^{2} =231.3056\).

Solución

Interpretando esto desde la forma exponencial básica, sabemos que 86 es nuestro valor inicial. Esto significa que el 1 de enero de 2016 esta región tenía 86 mil contratos de teléfonos inteligentes Android. Ya que\(b = 1 + r = 1.64\), sabemos que cada trimestre el número de contratos de teléfonos inteligentes crece 64%. \(T(2) = 231.3056\)significa que en el\(2^{nd}\) trimestre (o al final del segundo trimestre) hubo aproximadamente 231,306 contratos de teléfonos inteligentes Android.

Encontrar ecuaciones de funciones exponenciales

Funciones exponenciales:Encontrar ecuaciones

En los ejemplos anteriores, pudimos escribir ecuaciones para funciones exponenciales ya que conocíamos la cantidad inicial y la tasa de crecimiento. Si no conocemos la tasa de crecimiento, sino que conocemos solo algunos pares de valores de entrada y salida, aún podemos construir una función exponencial.

Ejemplo\(\PageIndex{5}\)

En 2009, 80 venados fueron reintroducidos en un área de refugio de vida silvestre de la cual la población había sido previamente cazada hasta su eliminación. Para 2015, la población había crecido a 180 venados. Si esta población crece exponencialmente, encuentra una fórmula para la función.

Solución

Al definir nuestra variable de entrada a ser\(t\), años después de 2009, la información listada puede escribirse como dos pares entrada-salida: (0,80) y (6,180). Observe que al elegir nuestra variable de entrada para ser medida como años después del valor del primer año proporcionado, efectivamente nos hemos “dado” el valor inicial para la función:\(a\) = 80. Esto nos da una ecuación de la forma

\[f(t)=80b^{t} \nonumber\]

Sustituir en nuestro segundo par entrada-salida nos permite resolver\(b\):

\[180=80b^{6}\nonumber\]Dividir por 80
\[b^{6} =\dfrac{180}{80} =\dfrac{9}{4}\nonumber\] Toma la\({}^{th}\) raíz 6 de ambos lados.
\[b=\sqrt[{6}]{\dfrac{9}{4} } =1.1447\nonumber\]

Esto nos da nuestra ecuación para la población:

\[f(t)=80(1.1447)^{t}\nonumber\]

Recordemos que ya que\(b = 1+r\), podemos interpretar esto para significar que la tasa de crecimiento poblacional es\(r\) = 0.1447, y así la población está creciendo alrededor de 14.47% cada año.

En este ejemplo, también podrías haber usado (9/4) ^ (1/6) para evaluar la\({}^{th}\) raíz 6 si tu calculadora no tiene un botón\({n}^{th}\) raíz.

En el ejemplo anterior, optamos por usar la\(f(x)=ab^{x}\) forma de la función exponencial en lugar de la\(f(x)=a(1+r)^{x}\) forma. Esta elección fue completamente arbitraria — cualquiera de las formas estaría bien de usar.

Al encontrar ecuaciones, el valor para\(b\) o generalmente\(r\) tendrá que ser redondeado para ser escrito fácilmente. Para preservar la precisión, es importante no sobrepasar estos valores. Por lo general, desea asegurarse de conservar al menos 3 dígitos significativos en la tasa de crecimiento. Por ejemplo, si tu valor para\(b\) era 1.00317643, no querrías redondear esto más allá de 1.00318.

En el ejemplo anterior, pudimos “darnos” el valor inicial mediante una definición inteligente de nuestra variable de entrada. A continuación, consideramos una situación en la que no podemos hacer esto.

Ejemplo\(\PageIndex{6}\)

Encuentra una fórmula para una función exponencial que pasa por los puntos (-2,6) y (2,1).

Solución

Como no tenemos el valor inicial, tomaremos un enfoque general que funcionará para cualquier forma de función con parámetros desconocidos: sustituiremos en ambos pares de entrada-salida dados en la forma de función\(f(x)=ab^{x}\) y resolveremos los valores desconocidos,\(a\) y\(b\).

Sustituir en (-2, 6) da\(6=ab^{-2}\)
Sustituir en (2, 1) da\(1=ab^{2}\)

Ahora los resolvemos como un sistema de ecuaciones. Para ello, podríamos intentar un enfoque de sustitución, resolviendo una ecuación por una variable, luego sustituyendo esa expresión por la segunda ecuación.

Resolviendo\(6=ab^{-2}\) para\(a\):

\[a=\dfrac{6}{b^{-2} } =6b^{2}\nonumber\]

En la segunda ecuación,\(1=ab^{2}\), sustituimos la expresión anterior por\(a\):

\[\begin{array}{l} {1=(6b^{2} )b^{2} } \\ {1=6b^{4} } \\ {\dfrac{1}{6} =b^{4} } \\ {b=\sqrt[{4}]{\dfrac{1}{6} } \approx 0.6389} \end{array}\nonumber\]

Volviendo a la ecuación nos\(a=6b^{2}\) permite encontrar\(a\):

\[a=6b^{2} =6(0.6389)^{2} =2.4492\nonumber\]

Armando esto da la ecuación\(f(x)=2.4492(0.6389)^{x}\)

Ejercicio\(\PageIndex{4}\)

Dados los dos puntos (1, 3) y (2, 4.5) encontramos la ecuación de una función exponencial que pasa por estos dos puntos.

Contestar

\(3=ab^{1}\), entonces\(a=\dfrac{3}{b}\),

\(4.5=ab^{2}\), entonces\(4.5=\dfrac{3}{b} b^{2}\). \(4.5=3b\)

\(b = 1.5\). \(a=\dfrac{3}{1.5} =2\)

\(f(x)=2\left(1.5\right)^{x}\)

Ejemplo\(\PageIndex{7}\)

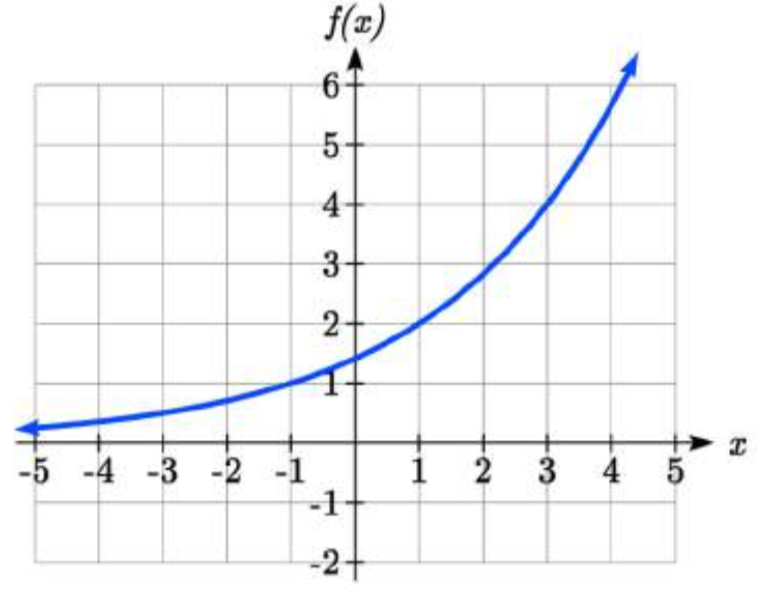
Encuentra una ecuación para la función exponencial graficada.

Solución

El valor inicial de la función no está claro en esta gráfica, por lo que en su lugar trabajaremos usando dos puntos más claros. Hay tres puntos claros: (-1, 1), (1, 2) y (3, 4). Como vimos en el último ejemplo, dos puntos son suficientes para encontrar la ecuación para un exponencial estándar, por lo que usaremos estos dos últimos puntos.

Sustituir en (1,2) da\(2=ab^{1}\)
Sustituir en (3,4) da\(4=ab^{3}\)

Resolviendo la primera ecuación para\(a\) da\(a=\dfrac{2}{b}\).

Sustituyendo esta expresión por a en la segunda ecuación:

\[4=ab^{3}\nonumber\]
\[4=\dfrac{2}{b} \quad b^{3} =\dfrac{2b^{3} }{b}\nonumber\]Simplificar el lado derecho
\[4 = 2b^2\nonumber\]
\[2 = b^2\nonumber\]
\[b = \pm \sqrt{2}\nonumber\]

Ya que nos limitamos a valores positivos de\(b\), vamos a utilizar\(b=\sqrt{2}\). Luego podemos regresar y encontrar\(a\):

\[a=\dfrac{2}{b} =\dfrac{2}{\sqrt{2} } =\sqrt{2}\nonumber \]

Esto nos da una ecuación final de\(f(x)=\sqrt{2} (\sqrt{2} )^{x}\).

Interés Compuesto

En el ejemplo de certificado bancario de depósito (CD) anterior en la sección, encontramos interés compuesto. Por lo general, las cuentas bancarias y otros instrumentos de ahorro en los que se reinvierten ganancias, como los fondos mutuos y las cuentas de jubilación, utilizan intereses compuestos. El término\(compounding\) proviene del comportamiento de que se ganan intereses no sobre el valor original, sino sobre el valor acumulado de la cuenta.

En el ejemplo de antes, el interés se compuso mensualmente, por lo que tomamos la tasa de interés anual, generalmente llamada tasa nominal o tasa porcentual anual (TAE) y dividida por 12, el número de compuestos en un año, para encontrar el interés mensual. El exponente se midió luego en meses.

Generalizando esto, podemos formar una fórmula general para el interés compuesto. Si la TAE se escribe en forma decimal como\(r\), y hay periodos\(k\) compuestos por año, entonces los intereses por periodo compuesto serán\(r/k\). De igual manera, si nos interesa el valor después de\(t\) años, entonces habrá periodos\(kt\) compuestos en ese tiempo.

Definición: Fórmula de interés compuesto

El interés compuesto se puede calcular usando la fórmula

\[A(t)=a\left(1+\dfrac{r}{k} \right)^{kt}\]

Dónde\(A(t)\) está el valor de la cuenta

• \(t\)se mide en años
• \(a\)es el monto inicial de la cuenta, a menudo llamado principal
• \(r\)es la tasa porcentual anual (TAE), también llamada tasa nominal
• \(k\)es el número de períodos compuestos en un año

Ejemplo\(\PageIndex{8}\)

Si invierte $3,000 en una cuenta de inversión pagando 3% de interés compuesto trimestralmente, ¿cuánto valdrá la cuenta en 10 años?

Solución

Ya que estamos empezando con $3000,\(a = 3000\)

Nuestra tasa de interés es del 3%, entonces\(r = 0.03\)

Como estamos componiendo trimestralmente, estamos componiendo 4 veces al año, por lo que\(k = 4\)

Queremos conocer el valor de la cuenta en 10 años, así que estamos buscando\(A(10)\), el valor cuando\(t = 10\).

\[A(10)=3000\left(1+\dfrac{0.03}{4} \right)^{4(10)} =\$ 4045.05\nonumber\]

La cuenta tendrá un valor de 4045.05 dólares en 10 años.

Ejemplo\(\PageIndex{9}\)

Un plan 529 es un plan de ahorro universitario en el que un familiar puede invertir dinero para pagar la matrícula universitaria posterior de un niño, y la cuenta crece libre de impuestos. Si Lily quiere configurar una cuenta 529 para su nueva nieta, quiere que la cuenta crezca a 40,000 dólares en 18 años, y cree que la cuenta ganará 6% compuesto semestral (dos veces al año), ¿cuánto necesitará Lily para invertir en la cuenta ahora?

Solución

Dado que la cuenta está ganando 6%,\(r = 0.06\)

Dado que los intereses se suman dos veces al año,\(k = 2\)

En este problema, no sabemos con qué tanto estamos empezando, así que vamos a estar resolviendo por un, la cantidad inicial necesaria. Sabemos que queremos que el monto final sea de $40.000, así que vamos a estar buscando el valor de un para que\(A(18) = 40,000\).

\[\begin{array}{l} {40,000=A(18)=a\left(1+\dfrac{0.06}{2} \right)^{2(18)} } \\ {40,000=a(2.8983)} \\ {a=\dfrac{40,000}{2.8983} \approx \$ 13,801} \end{array}\nonumber \]

Lily necesitará invertir 13.801 dólares para tener 40,000 dólares en 18 años.

Ejercicio\(\PageIndex{5}\)

Recalcular el ejemplo 2 desde arriba con la composición trimestral.

Contestar

24 meses = 2 años. \(1000\left(1+\dfrac{.012}{4} \right)^{4(2)}\)= $1024.25

Debido a la capitalización a lo largo del año, con interés compuesto el incremento real en un año es mayor que la tasa porcentual anual. Si se invirtieron $1,000 al 10%, la siguiente tabla muestra el valor después de 1 año a diferentes frecuencias de composición:

Frecuencia	Valor después de 1 año
Anualmente	$1100
Semestral	$1102.50
Trimestral	$1103.81
Mensual	$1104.71
Diario	$1105.16

Si tuviéramos que calcular el incremento porcentual real para la composición diaria, hubo un incremento de $105.16 a partir de un monto original de $1,000, para un incremento porcentual de\(\dfrac{105.16}{1000} =0.10516\) = 10.516%. Esta cantidad se denomina rendimiento porcentual anual (APY).

Observe que dado cualquier monto inicial, el monto después de 1 año sería

\(A(1)=a\left(1+\dfrac{r}{k} \right)^{k}\). Para encontrar el cambio total, restaríamos el monto original, luego para encontrar el cambio porcentual lo dividiríamos por el monto original:

\[\dfrac{a\left(1+\dfrac{r}{k} \right)^{k} -a}{a} =\left(1+\dfrac{r}{k} \right)^{k} -1\]

Rendimiento porcentual anual

El rendimiento porcentual anual (APY) es el porcentaje real que aumenta una cantidad en un año. Se puede calcular como

\[APY=\left(1+\dfrac{r}{k} \right)^{k} -1 \label{APY}\]

Esto equivale a encontrar el valor de $1 después de 1 año, y restar el dólar original.

Ejemplo\(\PageIndex{10}\)

El Banco A ofrece una cuenta pagando 1.2% compuesto trimestralmente. El Banco B ofrece una cuenta pagando 1.1% compuesto mensualmente. ¿Cuál es ofrecer una mejor tarifa?

Solución

Podemos comparar estas tasas usando el rendimiento porcentual anual, el incremento porcentual real en un año.

• Banco A:\(APY=\left(1+\dfrac{0.012}{4} \right)^{4} -1=0.012054\) = 1.2054%
• Banco B:\(APY=\left(1+\dfrac{0.011}{12} \right)^{12} -1=0.011056\) = 1.1056%

La capitalización mensual del Banco B no es suficiente para ponerse al día con la mejor APR del Banco A. El Banco A ofrece una mejor tasa.

Un límite a la composición

Como vimos antes, la cantidad que ganamos aumenta a medida que aumentamos la frecuencia de composición. La tabla, sin embargo, muestra que el incremento de la composición anual a semestral es mayor que el incremento de la composición mensual a la diaria. Esto podría llevarnos a creer que si bien aumentar la frecuencia de la composición aumentará nuestro resultado, hay un límite superior para este proceso.

Para ver esto, examinemos el valor de $1 invertido al 100% de interés por 1 año.

Frecuencia	Valor
Anual	$2
Trimestral	$2.441406
Mensual	$2.613035
Diario	$2.714567
Por hora	$2.718127
Una vez por minuto	$2.718279
Una vez por segundo	$2.718282

Estos valores sí parecen estar acercándose a un límite superior. Este valor termina siendo tan importante que se representa por su propia letra, al igual que cómo\(\pi\) representa un número.

Definición: Número de Euler:\(e\)

\(e\)es la letra utilizada para representar el valor que se\(\left(1+\dfrac{1}{k} \right)^{k}\) acerca a medida que\(k\) se hace grande.

\[e \approx 2.718282\nonumber\]

Debido a que a menudo\(e\) se usa como base de un exponencial, la mayoría de las calculadoras científicas y gráficas tienen un botón que puede calcular potencias de\(e\), generalmente etiquetadas\({e}^{x}\). Algunos programas informáticos en su lugar define una función\(exp(x)\), donde\(exp(x) = {e}^{x}\).

Porque\(e\) surge cuando el tiempo entre compuestos se vuelve muy pequeño, nos\(e\) permite definir el crecimiento continuo y nos permite definir una nueva función de kit de herramientas,\(f(x)=e^{x}\).

Definición: Fórmula de crecimiento continuo

El crecimiento continuo se puede calcular usando la fórmula

\[f(x)=ae^{rx}\nonumber\]

donde

\(a\)es la cantidad inicial

\(r\)es la tasa de crecimiento continuo

Este tipo de ecuación se usa comúnmente cuando se describen cantidades que cambian más o menos continuamente, como reacciones químicas, crecimiento de grandes poblaciones y desintegración radiactiva.

Ejemplo\(\PageIndex{11}\)

El radón-222 decae a una tasa continua de 17.3% por día. ¿A cuánto se desintegrarán 100mg de Radón-222 en 3 días?

Solución

Dado que se nos da una tasa de decaimiento continuo, utilizamos la fórmula de crecimiento continuo. Dado que la sustancia está en descomposición, sabemos que la tasa de crecimiento será negativa:\(r\) = -0.173

\(f(3)=100e^{-0.173(3)} \approx 59.512\)Quedarán mg de Radón-222.

Ejercicio\(\PageIndex{6}\)

Interpreta lo siguiente:\(S(t)=20e^{0.12t}\) si\(S(t)\) representa el crecimiento de una sustancia en gramos, y el tiempo se mide en días.

Contestar

Una sustancia inicial que pesa 20g está creciendo a una tasa continua de 12% por día.

El crecimiento continuo también se aplica a menudo al interés compuesto, lo que nos permite hablar de composición continua.

Ejemplo\(\PageIndex{12}\)

Si se invierte $1000 en una cuenta que gana 10% compuesta continuamente, encuentre el valor después de 1 año.

Solución

Aquí, la tasa de crecimiento continuo es del 10%, por lo que\(r\) = 0.10. Empezamos con $1000, entonces\(a\) = 1000.

Para encontrar el valor después de 1 año,

\[f(1)=1000e^{0.10(1)} \approx \$ 1105.17\nonumber\]

Observe que esto es un incremento de $105.17 para el año. Como incremento porcentual, esto es\(\dfrac{105.17}{1000} =0.10517=10.517\%\) incremento sobre los $1000 originales.

Observe que este valor es ligeramente mayor que la cantidad generada por la composición diaria en la tabla calculada anteriormente.

La tasa de crecimiento continuo es como la tasa de crecimiento nominal (o TAE) — refleja la tasa de crecimiento antes de que la composición entre en vigor. Esto es diferente a la tasa de crecimiento anual utilizada en la fórmula\(f(x)=a(1+r)^{x}\), que es como el rendimiento porcentual anual —refleja la cantidad real que crece la producción en un año.

Si bien la tasa de crecimiento continuo en el ejemplo anterior fue de 10%, el rendimiento anual real fue de 10.517%. Esto significa que podríamos escribir dos fórmulas de aspecto diferente pero equivalentes para el crecimiento de esta cuenta:

\(f(t)=1000e^{0.10t}\)utilizando la tasa de crecimiento continuo del 10%
\(f(t)=1000(1.10517)^{t}\) utilizando la tasa de rendimiento anual real de 10.517%.

Temas Importantes de esta Sección

• Porcentaje de crecimiento
• Funciones exponenciales
• Encontrar fórmulas
• Interpretación de ecuaciones
• Gráficas
• Crecimiento y Decaimiento Exponencial
• Interés compuesto
• Rendimiento porcentual anual
• Crecimiento Continuo