4.4: Propiedades logarítmicas

En la sección anterior, derivamos dos importantes propiedades de logaritmos, lo que nos permitió resolver algunas ecuaciones exponenciales y logarítmicas básicas.

propiedades de troncos

Propiedades inversas:

\[\log _{b} \left(b^{x} \right)=x\]

\[b^{\log _{b} x} =x\]

Propiedad Exponencial:

\[\log _{b} \left(A^{r} \right)=r\log _{b} \left(A\right)\]

Cambio de Base:

\[\log _{b} \left(A\right)=\dfrac{\log _{c} (A)}{\log _{c} (b)}\]

Si bien estas propiedades nos permiten resolver un gran número de problemas, no son suficientes para resolver todos los problemas que involucran ecuaciones exponenciales y logarítmicas.

propiedades de troncos

Propiedad Suma de Registros:

\[\log _{b} \left(A\right)+\log _{b} \left(C\right)=\log _{b} (AC)\]

Diferencia de Propiedad de Registros:

\[\log _{b} \left(A\right)-\log _{b} \left(C\right)=\log _{b} \left(\dfrac{A}{C} \right) \]

Es tan importante saber qué propiedades logaritmos no satisfacen como memorizar las propiedades válidas enumeradas anteriormente. En particular, el logaritmo no es una función lineal, lo que significa que no distribuye:

\[\log A + B \ne \log A + \log B. \label{distr1}\]

Para ayudar en este proceso ofrecemos una prueba de Ecuación\ ref {distr1} para ayudar a solidificar nuestras nuevas reglas y mostrar cómo se siguen de las propiedades que ya has visto.

Prueba

Dejar\(a=\log _{b} \left(A\right)\) y\(c=\log _{b} \left(C\right)\).

Por definición del logaritmo,\(b^{a} =A\) y\(b^{c} =C\).

Usando estas expresiones,

\[AC=b^{a} b^{c} \nonumber\]

Usando reglas de exponente a la derecha,

\[AC=b^{a+c} \nonumber\]

Tomando el tronco de ambos lados, y utilizando la propiedad inversa de los troncos,

\[\log _{b} \left(AC\right)=\log _{b} \left(b^{a+c} \right)=a+c \nonumber\]

Sustitución\(a\) y\(c\) con su definición establece el resultado

\[\log _{b} \left(AC\right)=\log _{b} A+\log _{b} C \nonumber\]

El comprobante de la propiedad de diferencia es muy similar.

Con estas propiedades, podemos reescribir expresiones que involucran múltiples registros como un solo registro, o romper una expresión que involucra un solo registro en expresiones que involucran múltiples registros.

Ejemplo\(\PageIndex{1}\)

Escribir\(\log _{3} \left(5\right)+\log _{3} \left(8\right)-\log _{3} \left(2\right)\) como un solo logaritmo.

Solución

Usando la suma de los registros propiedad en los dos primeros términos,

\[\log _{3} \left(5\right)+\log _{3} \left(8\right)=\log _{3} \left(5\cdot 8\right)=\log _{3} \left(40\right) \nonumber\]

Esto reduce nuestra expresión original a

\[\log _{3} \left(40\right)-\log _{3} \left(2\right) \nonumber\]

Luego usando la diferencia de propiedad de registros,

\[\log _{3} \left(40\right)-\log _{3} \left(2\right)=\log _{3} \left(\dfrac{40}{2} \right)=\log _{3} \left(20\right) \nonumber\]

Ejemplo\(\PageIndex{2}\)

Evaluar\(2\log \left(5\right)+\log \left(4\right)\) sin calculadora reescribiendo primero como un logaritmo único.

Solución

En el primer término, podemos usar la propiedad exponente de los registros para escribir

\[2\log \left(5\right)=\log \left(5^{2} \right)=\log \left(25\right) \nonumber\]

Con la expresión reducida a una suma de dos registros\(\log \left(25\right)+\log \left(4\right)\),, podemos utilizar la propiedad sum of logs

\[\log \left(25\right)+\log \left(4\right)=\log (4\cdot 25)=\log (100) \nonumber\]

Ya que\(100 = 10^2\), podemos evaluar este registro sin una calculadora:

\[\log (100)=\log \left(10^{2} \right)=2 \nonumber\]

Ejercicio\(\PageIndex{1}\)

Sin una calculadora evalúe primero reescribiendo como un solo logaritmo:

\[\log _{2} \left(8\right)+\log _{2} \left(4\right)\nonumber\]

Responder

\[\log _{2} \left(8\cdot 4\right)=\log _{2} \left(32\right)=\log _{2} \left(2^{5} \right)=5 \nonumber\]

Ejemplo\(\PageIndex{3}\)

Reescribir\(\ln \left(\dfrac{x^{4} y}{7} \right)\) como suma o diferencia de registros

Solución

Primero, notando que tenemos un cociente de dos expresiones, podemos utilizar la propiedad de diferencia de los registros para escribir

\[\ln \left(\dfrac{x^{4} y}{7} \right)=\ln \left(x^{4} y\right)-\ln (7) \nonumber\]

Después viendo el producto en el primer término, usamos la propiedad sum

\[\ln \left(x^{4} y\right)-\ln (7)=\ln \left(x^{4} \right)+\ln (y)-\ln (7)\nonumber\]

Por último, podríamos usar la propiedad exponente en el primer término

\[\ln \left(x^{4} \right)+\ln (y)-\ln (7)=4\ln (x)+\ln (y)-\ln (7) \nonumber\]

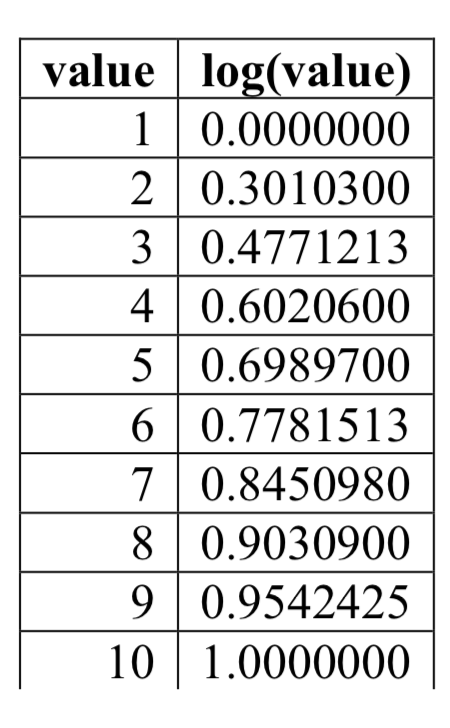De manera interesante, resolver ecuaciones exponenciales no fue la razón por la que los logaritmos se desarrollaron originalmente. Históricamente, hasta el advenimiento de las calculadoras y las computadoras, el poder de los logaritmos era que estas propiedades logarítmicas redujeron la multiplicación, división, raíces o potencias para ser evaluadas mediante suma, resta, división y multiplicación, respectivamente, las cuales son mucho más fáciles de calcular sin una calculadora. Se publicaron libros grandes en los que se enumeraban los logaritmos de los números, como en la tabla de la derecha. Para encontrar el producto de dos números, se utilizó la suma de propiedad de registro. Supongamos por ejemplo que no conocíamos el valor de 2 veces 3. Usando la propiedad sum de logs:

\[\log (2\cdot 3)=\log (2)+\log (3)\nonumber\]

Usando la tabla de registro,\[\log (2\cdot 3)=\log (2)+\log (3)=0.3010300+0.4771213=0.7781513\nonumber \]

Entonces podemos usar la tabla nuevamente a la inversa, buscando 0.7781513 como salida del logaritmo. A partir de eso podemos determinar:

\[\log (2\cdot 3)=0.7781513=\log (6).\nonumber\]

Mediante el uso de suma y la tabla de registros, pudimos determinar\(2\cdot 3=6\).

Del mismo modo, para calcular una raíz cubo como\(\sqrt[{3}]{8}\)

\[\log (\sqrt[{3}]{8} ) =\log \left(8^{1/3} \right)=\dfrac{1}{3} \log (8)=\dfrac{1}{3} (0.9030900)=0.3010300=\log (2) \nonumber\]

Entonces\(\sqrt[{3}]{8} =2\).

Aunque estos cálculos son simples e insignificantes, ilustran la misma idea que se utilizó durante cientos de años como una forma eficiente de calcular el producto, cociente, raíces y potencias de números grandes y complicados, ya sea usando tablas de logaritmos o herramientas mecánicas llamadas reglas de cálculo.

Estas propiedades aún tienen otras aplicaciones prácticas para interpretar cambios en las relaciones exponenciales y logarítmicas.

Ejemplo\(\PageIndex{4}\)

Recordemos que en química, la escala de pH se utiliza para cuantificar ácidos

\[pH=-\log \left(\left[H^{+} \right]\right). \nonumber\]

Si se duplica la concentración de iones hidrógeno en un líquido, ¿cuál es el efecto sobre el pH?

Solución

Supongamos que\(C\) es la concentración original de iones hidrógeno, y\(P\) es el pH original del líquido, entonces\(P=-\log \left(C\right)\). Si se duplica la concentración, la nueva concentración es\(2C\). Entonces el pH del nuevo líquido es

\[pH=-\log \left(2C\right) \nonumber\]

Usando la propiedad sum de los registros,

\[pH=-\log \left(2C\right)=-\left(\log (2)+\log (C)\right)=-\log (2)-\log (C) \nonumber\]

Ya que\(P=-\log \left(C\right)\), el nuevo pH es

\[pH=P-\log (2)=P-0.301 \nonumber\]

Cuando se duplica la concentración de iones hidrógeno, el pH disminuye en 0.301.

Propiedades de registro en Resolviendo ecuaciones

Las propiedades logarítmicas a menudo surgen al resolver problemas que involucran logaritmos. Primero, veremos una ecuación logarítmica más simple.

Ejemplo\(\PageIndex{5}\)

Resolver\(\log (2x-6)=3\).

Solución

Para resolverlo\(x\), necesitamos sacarlo desde dentro de la función log. Hay dos formas en las que podemos abordar esto.

Método 1: Reescribir como exponencial.

Recordemos que dado que el log común es base 10, se\(\log (A)=B\) puede reescribir como el exponencial\(10^{B} =A\). Así mismo, se\(\log (2x-6)=3\) puede reescribir en forma exponencial como

\[10^{3} =2x-6 \nonumber\]

Método 2: Exponenciar ambos lados.

Si\(A=B\), entonces\(10^{A} =10^{B}\). Usando esta idea, desde\(\log (2x-6)=3\), entonces\(10^{\log (2x-6)} =10^{3}\). Utilice la propiedad inversa de los registros para reescribir el lado izquierdo y obtener\(2x-6=10^{3}\).

Usando cualquiera de los dos métodos, ahora necesitamos resolver\(2x-6=10^{3}\). Evaluar\(10^{3}\) para obtener

\[2x-6=1000\nonumber\]Agregar 6 a ambos lados
\[2x=1006\nonumber\] Divide ambos lados por 2
\[x=503\nonumber\]

Ocasionalmente, el proceso de resolución dará como resultado soluciones extrañas, respuestas que están fuera del dominio de la ecuación original. En este caso, nuestra respuesta se ve bien.

Ejemplo\(\PageIndex{6}\)

Resolver\(\log (50x+25)-\log (x)=2\).

Solución

Para reescribir en forma exponencial, necesitamos una sola expresión logarítmica en el lado izquierdo de la ecuación. Usando la propiedad difference de logs, podemos reescribir el lado izquierdo:

\[\log \left(\dfrac{50x+25}{x} \right)=2 \nonumber\]

Reescribir en forma exponencial reduce esto a una ecuación algebraica:

\[\dfrac{50x+25}{x} =10^{2} =100\nonumber\]Multiplica ambos lados por\(x\)
\[50x+25=100x\nonumber\] Combinar términos similares
\[25=50x\nonumber\] Dividir por 50
\[x=\dfrac{25}{50} =\dfrac{1}{2}\nonumber\]

Al verificar esta respuesta en la ecuación original, podemos verificar que no hay problemas de dominio, y esta respuesta es correcta.

Ejercicio\(\PageIndex{2}\)

Resolver\(\log (x^{2} -4)=1+\log (x+2)\).

Responder

\[\log (x^{2} -4)=1+\log (x+2)\nonumber\]Mover ambos troncos a un lado

\[\log \left(x^{2} -4\right)-\log \left(x+2\right)=1\nonumber\]Usar la propiedad de diferencia de los registros

\[\log \left(\dfrac{x^{2} -4}{x+2} \right)=1\nonumber\]Factor

\[\log \left(\dfrac{(x+2)(x-2)}{x+2} \right)=1\nonumber\]Simplificar

\[\log \left(x-2\right)=1\nonumber\]Reescribir como exponencial

\[10^{1} =x-2\nonumber\]Agregar 2 a ambos lados

\[x=12\nonumber\]

Ejemplo\(\PageIndex{7}\)

Resolver\(\ln (x+2)+\ln (x+1)=\ln (4x+14)\).

Solución

\[\ln (x+2)+\ln (x+1)=\ln (4x+14)\nonumber\]Utilice la propiedad de suma de registros a la derecha
\[\ln \left((x+2)(x+1)\right)=\ln (4x+14)\nonumber\] Ampliar
\[\ln \left(x^{2} +3x+2\right)=\ln (4x+14)\nonumber\]

Tenemos un registro en ambos lados de la ecuación esta vez. Reescribir en forma exponencial sería complicado, así que en su lugar podemos exponenciar ambos lados.

\[e^{\ln \left(x^{2} +3x+2\right)} =e^{\ln (4x+13)}\nonumber\]Usar la propiedad inversa de logs
\[x^{2} +3x+2=4x+14\nonumber\] Mover términos a un lado
\[x^{2} -x-12=0\nonumber\] Factor
\[(x+4)(x-3)=0\nonumber\]
\[x = -4\text{ or }x = 3\nonumber \]

Al verificar nuestras respuestas, observe que evaluar la ecuación original en\(x = -4\) resultaría en que evaluáramos\(\ln (-2)\), lo cual no está definido. Esa respuesta está fuera del dominio de la ecuación original, por lo que es una solución extraña y la descartamos. Hay una solución:\(x = 3\).

Las ecuaciones exponenciales más complejas a menudo se pueden resolver de más de una manera. En el siguiente ejemplo, resolveremos el mismo problema de dos maneras: una usando propiedades logaritmos y la otra usando propiedades exponenciales.

Ejemplo\(\PageIndex{8a}\)

En 2008, la población de Kenia era de aproximadamente 38.8 millones, y crecía 2.64% cada año, mientras que la población de Sudán era de aproximadamente 41.3 millones y crecía 2.24% cada año (Banco Mundial, Indicadores de Desarrollo Mundial, como se informó en http://www.google.com/publicdata, recuperado agosto 24, 2010). Si estas tendencias continúan, ¿cuándo coincidirá la población de Kenia con la de Sudán?

Solución

Comenzamos por escribir una ecuación para cada población en términos de\(t\), el número de años después de 2008.

\[\begin{array}{l} {Kenya(t)=38.8(1+0.0264)^{t} } \\ {Sudan(t)=41.3(1+0.0224)^{t} } \end{array}\nonumber\]

Para encontrar cuando las poblaciones serán iguales, podemos establecer las ecuaciones iguales

\[38.8(1.0264)^{t} =41.3(1.0224)^{t} \nonumber\]

Para nuestro primer acercamiento, tomamos el log de ambos lados de la ecuación.

\[\log \left(38.8(1.0264)^{t} \right)=\log \left(41.3(1.0224)^{t} \right) \nonumber\]

Utilizando la propiedad sum de los registros, podemos reescribir cada lado,

\[\log (38.8)+\log \left(1.0264^{t} \right)=\log (41.3)+\log \left(1.0224^{t} \right)\nonumber\]

Luego, utilizando la propiedad del exponente, podemos sacar las variables del exponente

\[\log (38.8)+t\log \left(1.0264\right)=\log (41.3)+t\log \left(1.0224\right) \nonumber\]

Mover todos los términos que involucran\(t\) a un lado de la ecuación y el resto de los términos al otro lado,

\[t\log \left(1.0264\right)-t\log \left(1.0224\right)=\log (41.3)-\log (38.8) \nonumber\]

Factorizando el\(t\) de la izquierda,

\[t\left(\log \left(1.0264\right)-\log \left(1.0224\right)\right)=\log (41.3)-\log (38.8)\nonumber\]

Dividiendo para resolver\(t\)

\[t=\dfrac{\log (41.3)-\log (38.8)}{\log \left(1.0264\right)-\log \left(1.0224\right)} \approx 15.991\nonumber\]

Faltarán 15.991 años hasta que las poblaciones sean iguales.

Ejemplo\(\PageIndex{8b}\)

Resuelve el problema anterior reescribiendo antes de tomar el registro.

Solución

Comenzando en la ecuación

\[38.8(1.0264)^{t} =41.3(1.0224)^{t}\nonumber\]

Dividir para mover los términos exponenciales a un lado de la ecuación y las constantes al otro lado

\[\dfrac{1.0264^{t} }{1.0224^{t} } =\dfrac{41.3}{38.8}\nonumber\]

Usando reglas de exponente para agrupar a la izquierda,

\[\left(\dfrac{1.0264}{1.0224} \right)^{t} =\dfrac{41.3}{38.8}\nonumber\]

Tomando el tronco de ambos lados

\[\log \left(\left(\dfrac{1.0264}{1.0224} \right)^{t} \right)=\log \left(\dfrac{41.3}{38.8} \right)\nonumber\]

Utilizando la propiedad de exponente a la izquierda,

\[t\log \left(\dfrac{1.0264}{1.0224} \right)=\log \left(\dfrac{41.3}{38.8} \right)\nonumber\]

Dividir da

\[t=\dfrac{\log \left(\dfrac{41.3}{38.8} \right)}{\log \left(\dfrac{1.0264}{1.0224} \right)} \approx 15.991\text{ years}\nonumber\]

Si bien la respuesta no aparece inmediatamente idéntica a la producida usando el método anterior, tenga en cuenta que al usar la propiedad de diferencia de los registros, la respuesta podría reescribirse:

\[t=\dfrac{\log \left(\dfrac{41.3}{38.8} \right)}{\log \left(\dfrac{1.0264}{1.0224} \right)} =\dfrac{\log (41.3)-\log (38.8)}{\log (1.0264)-\log (1.0224)}\nonumber\]

Si bien ambos métodos funcionan igualmente bien, a menudo requiere menos pasos para utilizar álgebra antes de tomar registros, en lugar de depender únicamente de las propiedades del registro.

Ejercicio\(\PageIndex{3}\)

El Tanque A contiene 10 litros de agua, y 35% del agua se evapora cada semana. El Tanque B contiene 30 litros de agua, y el 50% del agua se evapora cada semana. ¿En cuántas semanas contendrán los tanques la misma cantidad de agua?

Responder

Tanque A:\(A(t)=10(1-0.35)^{t}\). Tanque B:\(B(t)=30(1-0.50)^{t}\)

Resolviendo A (t) = B (t),

\[10(0.65)^{t} =30(0.5)^{t}\nonumber\]Usando el método del Ejemplo 8b

\[\frac{(0.65)^{t}}{(0.5)^{t}} =\dfrac{30}{10}\nonumber\]Reagruparse

\[\left(\dfrac{0.65}{0.5} \right)^{t} =3\nonumber\]Simplificar

\[\left(1.3\right)^{t} =3\nonumber\]Tome el tronco de ambos lados

\[\log \left(\left(1.3\right)^{t} \right)=\log \left(3\right)\nonumber\]Usar la propiedad exponente de los registros

\[t\log \left(1.3\right)=\log \left(3\right)\nonumber\]Dividir y evaluar

\[t=\dfrac{\log \left(3\right)}{\log \left(1.3\right)} \approx 4.1874\text{ weeks}\nonumber\]

Temas Importantes de esta Sección

• Inversa
• Exponencial
• Cambio de base
• Suma de registros de propiedad
• Diferencia de propiedad de registros