4.5: Gráficas de funciones logarítmicas

Última actualización
Guardar como PDF

Page ID: 116808

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Recordemos que la función exponencial$f(x)=2^{x}$ produce esta tabla de valores

$x$	-3	-2	-1	0	1	2	3
$f(x)$	$\dfrac{1}{8}$	$\dfrac{1}{4}$	$\dfrac{1}{2}$	1	2	4	8

Dado que la función logarítmica es una inversa de la exponencial,$g(x)=\log _{2} (x)$ produce la tabla de valores

$x$	$\dfrac{1}{8}$	$\dfrac{1}{4}$	$\dfrac{1}{2}$	1	2	4	8
$g(x)$	-3	-2	-1	0	1	2	3

En esta segunda tabla, fíjese que

1. A medida que aumenta la entrada, la salida aumenta.
2. A medida que aumenta la entrada, la salida aumenta más lentamente.
3. Dado que la función exponencial solo genera valores positivos, el logaritmo solo puede aceptar valores positivos como entradas, por lo que el dominio de la función log es$(0,\infty )$.
4. Dado que la función exponencial puede aceptar todos los números reales como entradas, el logaritmo puede generar cualquier número real, por lo que el rango es todo números reales o$(-\infty ,\infty )$.

Al esbozar la gráfica, observe que a medida que la entrada se acerca a cero desde la derecha, la salida de la función crece muy grande en la dirección negativa, lo que indica una asíntota vertical en$x = 0$.

En notación simbólica escribimos como$x \to 0^{+} ,f(x) \to -\infty$, y como$x \to \infty ,f(x) \to \infty$

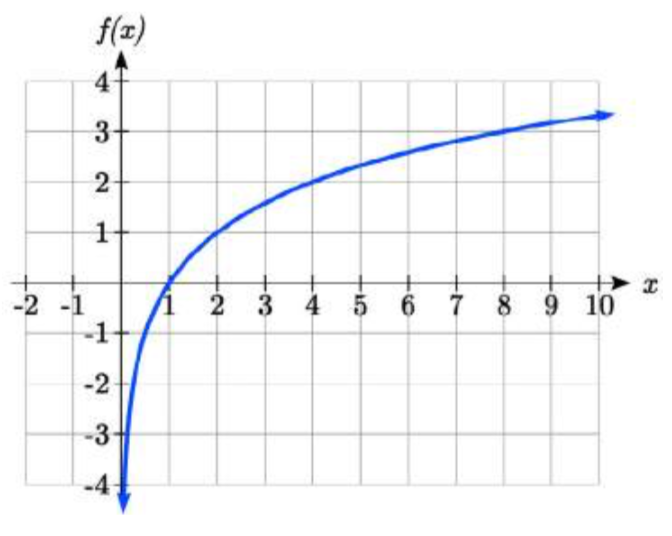
$Una gráfica que se acerca al infinito negativo a medida que x se acerca a 0 desde la derecha, y aumenta curvándose hacia abajo pasando por 1 coma 0, 2 coma 1, 4 coma 2 y 8 coma 3$

Características gráficas del logaritmo

Gráficamente, en la función$g(x)=\log _{b} (x)$
La gráfica tiene una intercepción horizontal en (1, 0)
La gráfica tiene una asíntota vertical en$x = 0$
La gráfica es creciente y cóncava hacia abajo
El dominio de la función es$x > 0$, o$(0,\infty )$
El rango de la función es todos los números reales, o$(-\infty ,\infty )$

Al esbozar un logaritmo general con base$b$, puede ser útil recordar que la gráfica pasará por los puntos (1, 0) y ($b$, 1). Para tener una idea de cómo la base afecta la forma de la gráfica, examine las gráficas a continuación.

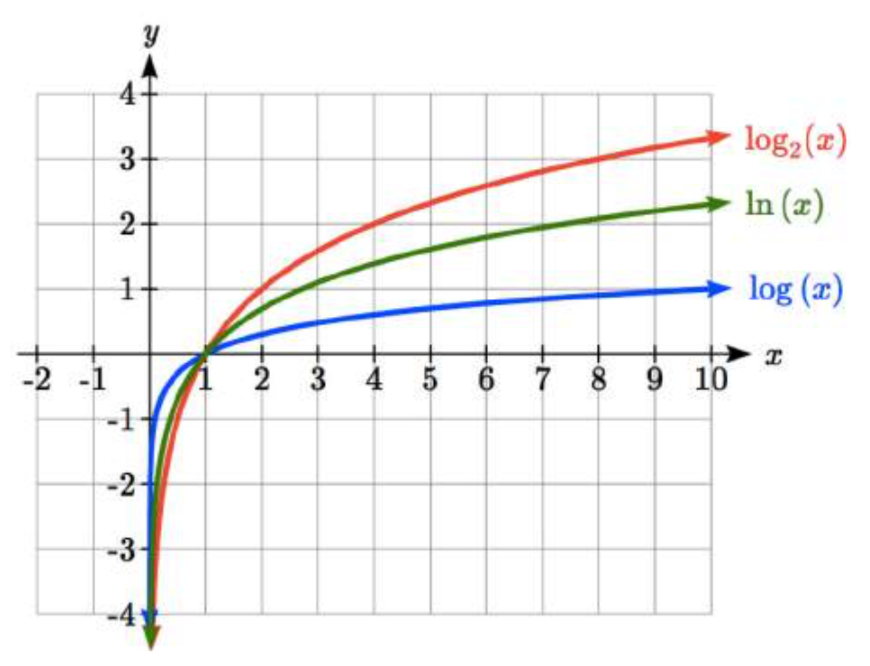
$Tres gráficas logarítmicas en los mismos ejes, todas ellas se acercan al infinito negativo a medida que x se acerca a 0 desde la derecha, y que aumentan curvándose hacia abajo, pasando todas por 1 coma 0. El primero, etiquetado log de x, aumenta más lentamente y pasa por 10 comas 1. El segundo, etiquetado ln de x, aumenta más rápidamente, y pasa por un punto alrededor de 2.818 coma 1. El tercero, etiquetado como base logarítmica 2 de x, aumenta más rápidamente y pasa por 2 coma 1.$

Observe que cuanto mayor sea la base, más lento crece el gráfico. Por ejemplo, la gráfica logarítmica común, mientras crece sin encuadernación, lo hace muy lentamente. Por ejemplo, para alcanzar una salida de 8, la entrada debe ser de 100,000,000.

Otra observación importante realizada fue el dominio del logaritmo. Al igual que las funciones recíprocas y de raíz cuadrada, el logaritmo tiene un dominio restringido que debe considerarse al encontrar el dominio de una composición que involucra un log.

Ejemplo$\PageIndex{1}$

Encuentra el dominio de la función$f(x)=\log (5-2x)$.

Solución

El logaritmo solo se define con la entrada es positiva, por lo que esta función solo se definirá cuando$5 - 2x > 0$. Resolviendo esta desigualdad,

\[\begin{align*} -2x &>-5 \\[4pt] x &< \dfrac{5}{2} \end{align*} \nonumber\]

El dominio de esta función es$x < \dfrac{5}{2}$, o en notación de intervalo,$\left(-\infty ,\dfrac{5}{2} \right)$

Ejercicio$\PageIndex{1}$

Encuentra el dominio de la función$f(x)=\log (x-5)+2$; antes de resolver esto como una desigualdad, considera cómo se ha transformado la función.

Responder: Dominio: {$x$|$x > 5$}

Transformaciones de la función logarítmica

Las transformaciones se pueden aplicar a una función logarítmica utilizando las técnicas básicas de transformación, pero al igual que con las funciones exponenciales, varias transformaciones dan como resultado relaciones interesantes.

Primero recordamos el cambio de propiedad base nos dice que:

\[\log _{b} x=\dfrac{\log _{c} x}{\log _{c} b} =\dfrac{1}{\log _{c} b} \log _{c} x \nonumber\]

A partir de esto, podemos ver que$\log _{b} x$ es un estiramiento vertical o compresión de la gráfica de la$\log _{c} x$ gráfica. Esto nos dice que un estiramiento o compresión vertical equivale a un cambio de base. Por esta razón, normalmente representamos todas las gráficas de funciones logarítmicas en términos de las funciones logarítmicas comunes o naturales.

A continuación, considere el efecto de una compresión horizontal en la gráfica de una función logarítmica. Considerando$f(x)=\log (cx)$, podemos usar la propiedad sum para ver

\[ \begin{align*} f(x) &=\log (cx) \\[4pt] &=\log (c)+\log (x) \end{align*}\]

Dado que log ($c$) es una constante, el efecto de una compresión horizontal es el mismo que el efecto de un desplazamiento vertical.

Ejemplo$\PageIndex{2}$

Sketch$f(x)=\ln (x)$ y$g(x)=\ln (x)+2$.

Solución

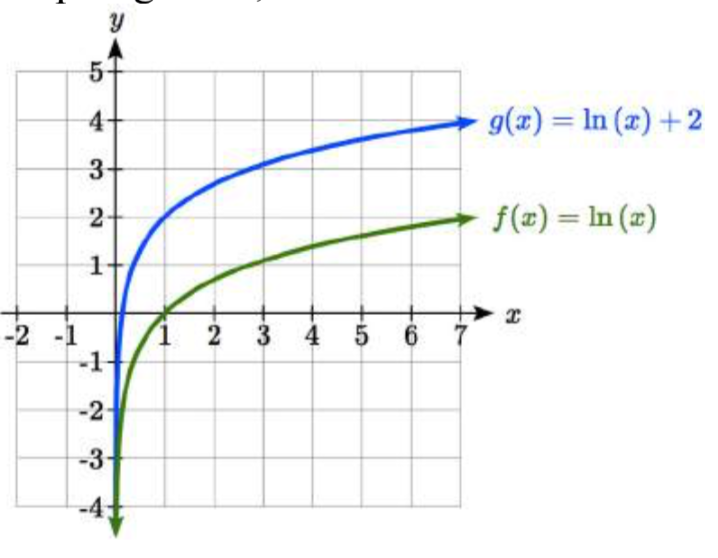
$Dos gráficas logarítmicas en los mismos ejes, ambas que se acercan al infinito negativo a medida que x se acerca a 0 desde la derecha, y que aumentan curvándose hacia abajo El primero marcado ln de x pasa por 1 coma 0 y 2.818 coma 1. El segundo marcado ln de x más 2 pasa por 1 coma 2 y 2.818 coma 3$

Graficando estos,

Obsérvese que este desplazamiento vertical también podría escribirse como una compresión horizontal, ya que$g(x)=\ln (x)+2=\ln (x)+\ln (e^{2} )=\ln (e^{2} x).$

Mientras que un estiramiento o compresión horizontal se puede escribir como un desplazamiento vertical, una reflexión horizontal es única y separada del desplazamiento vertical.

Finalmente, consideraremos el efecto de un desplazamiento horizontal en la gráfica de un logaritmo.

Ejemplo$\PageIndex{3}$

Esbozar una gráfica de$f(x)=\ln (x+2)$.

Solución

Se trata de un desplazamiento horizontal hacia la izquierda en 2 unidades. Observe que ninguna de nuestras reglas de logaritmo nos permite reescribir esto de otra forma, por lo que el efecto de esta transformación es único. Desviando la gráfica,

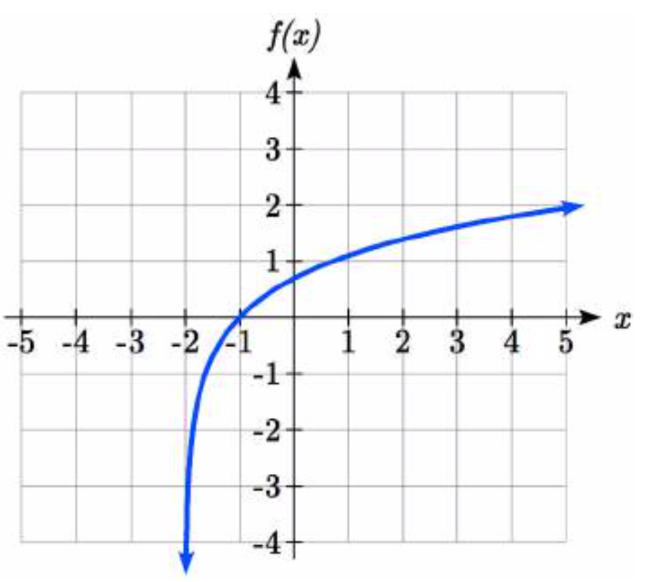
$Una gráfica que se acerca al infinito negativo a medida que x se acerca al negativo 2 desde la derecha, y aumenta curvándose hacia abajo pasando por negativo 1 coma 0 y 0.818 coma 1$

Observe que debido al desplazamiento horizontal, la asíntota vertical se desplazó a$x = -2$, y el dominio se desplazó a$(-2,\infty )$.

Combinando estas transformaciones,

Ejemplo$\PageIndex{4}$

Esbozar una gráfica de$f(x) = 5\log(-x + 2)$.

Solución

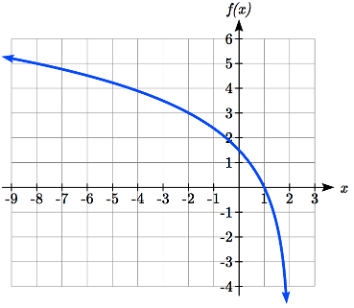
$Una gráfica que disminuye curvándose hacia abajo, pasando por negativo 8 coma 5 y 1 coma 0 y se acerca al infinito negativo a medida que x se acerca a 2 desde la izquierda.$

Factorizar el interior como$f (x) = 5\log(−(x − 2))$ revela que esta gráfica es la del logaritmo común, reflejada horizontalmente, estirada verticalmente por un factor de 5, y desplazada hacia la derecha en 2 unidades.

La asíntota vertical se desplazará a$x = 2$ y la gráfica tendrá dominio$(\infty, 2)$. Se puede crear un boceto rugoso usando la asíntota vertical junto con un par de puntos en la gráfica, como

\[ \begin{align*} (f (1) &= 5\log(−1+ 2) = 5\log(1) = 0 \\[4pt] f (−8) &= 5\log(−(−8) + 2) = 5\log(10) = 5 \end{align*}\]

Ejercicio$\PageIndex{2}$

Esboce una gráfica de la función$f(x)=-3\log (x-2)+1$.

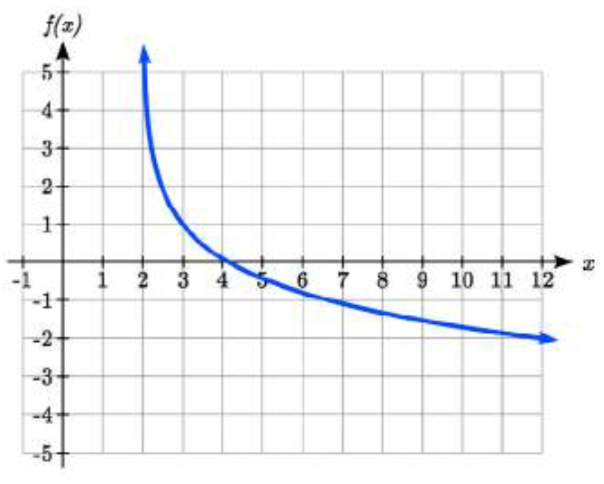
Responder: $Una gráfica que se acerca al infinito a medida que x se acerca a 2 desde la derecha y disminuye curvándose hacia arriba, pasando por 3 coma 1, 4 coma 0 y 12 coma negativa 2$

transormaciones de troncos

Cualquier función logarítmica transformada se puede escribir en la forma

\[f(x)=a\log (x-b)+k\text{ ,or }f(x)=a\log \left(-\left(x-b\right)\right)+k\]si se refleja horizontalmente,

donde$x = b$ está la asíntota vertical.

Ejemplo$\PageIndex{5}$

Encuentra una ecuación para la función logarítmica graficada.

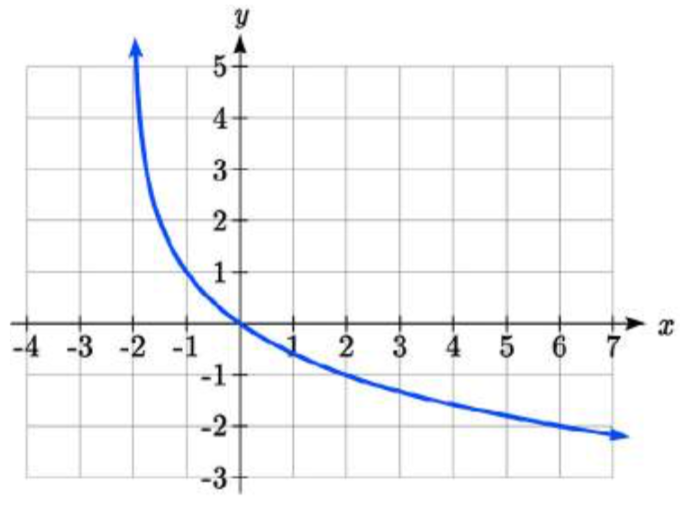
$Una gráfica que se acerca al infinito a medida que x se acerca al negativo 2 desde la derecha y disminuye curvándose hacia arriba, pasando por negativo 1 coma 1, 0 coma 0 y 2 coma negativa 1$

Solución

Esta gráfica tiene una asíntota vertical en$x = –2$ y se ha reflejado verticalmente. Aún no conocemos el desplazamiento vertical (equivalente al estiramiento horizontal) o el estiramiento vertical (equivalente a un cambio de base). Sabemos hasta ahora que la ecuación tendrá forma

\[f(x)=-a\log (x+2)+k\nonumber\]

Aparece que la gráfica pasa por los puntos (—1, 1) y (2, —1). Sustituyendo en (—1, 1),

\[\begin{array}{l} {1=-a\log (-1+2)+k} \\ {1=-a\log (1)+k} \\ {1=k} \end{array}\nonumber\]

A continuación, sustituyendo en (2, —1),

\[\begin{array}{l} {-1=-a\log (2+2)+1} \\ {-2=-a\log (4)} \\ {a=\dfrac{2}{\log (4)} } \end{array}\nonumber\]

Esto nos da la ecuación

\[f(x)=-\dfrac{2}{\log (4)} \log (x+2)+1. \nonumber\]

Esto también podría escribirse como

\[f(x)=-2\log _{4} (x+2)+1. \nonumber\]

Ejercicio$\PageIndex{3}$

Escribe una ecuación para la función graficada aquí.

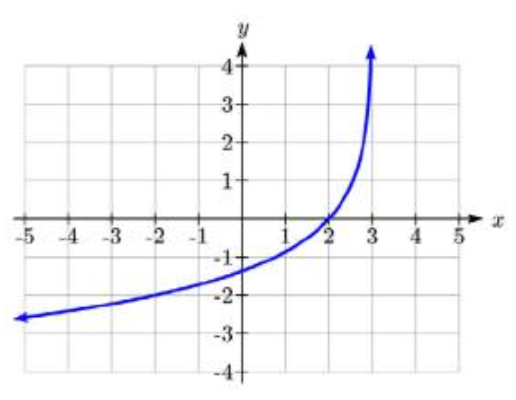
$Una gráfica que aumenta curvándose hacia arriba, pasando por negativo 2 coma negativo 2 y 2 coma 0, luego se acerca al infinito a medida que x se acerca a 3 desde la izquierda.$

Responder: La gráfica se refleja horizontalmente y tiene una asíntota vertical en$x = 3$, dando forma$f(x)=a\log \left(-\left(x-3\right)\right)+k$. Sustituyendo en el punto (2,0) da$0=a\log \left(-\left(2-3\right)\right)+k$, simplificando a$k = 0$. Sustituyendo en (-2, -2),\[-2=a\log \left(-\left(-2-3\right)\right)\nonumber\] entonces\[\dfrac{-2}{\log (5)} =a\nonumber\] La ecuación es\[f(x)=\dfrac{-2}{\log (5)} \log \left(-\left(x-3\right)\right)\nonumber\] o\[f(x)=-2\log _{5} \left(-\left(x-3\right)\right)\nonumber\]

flashback

Escriba el dominio y el rango de la función graficada en el Ejemplo 5, y describa su comportamiento a largo plazo.

Responder: Dominio: {$x$|$x$ > -2}, Rango: todos los números reales; Como$x\to -2^{+} ,f(x)\to \infty$ y como$x\to \infty ,f(x)\to -\infty$.

Temas Importantes de esta Sección

Gráfico de la función logarítmica (dominio y rango)
Transformación de funciones logarítmicas
Creación de gráficas a partir de ecuaciones
Creación de ecuaciones a partir de gráficas

\(x\)	-3	-2	-1	0	1	2	3
\(f(x)\)	\(\dfrac{1}{8}\)	\(\dfrac{1}{4}\)	\(\dfrac{1}{2}\)	1	2	4	8

\(x\)	\(\dfrac{1}{8}\)	\(\dfrac{1}{4}\)	\(\dfrac{1}{2}\)	1	2	4	8
\(g(x)\)	-3	-2	-1	0	1	2	3