7.4: Modelado de Amplitud Cambiante y Línea Media

Última actualización
Guardar como PDF

Page ID: 116638

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Sección 7.4 Modelado Cambio de Amplitud y Línea Media

Si bien las funciones sinusoidales pueden modelar una variedad de comportamientos, a menudo es necesario combinar funciones sinusoidales con curvas lineales y exponenciales para modelar aplicaciones y comportamientos reales. Comenzamos esta sección observando los cambios en la línea media de una función sinusoidal. Recordemos que la línea media describe el valor medio, o promedio, de la función sinusoidal.

Cambio de líneas medias

Ejemplo$\PageIndex{1}$

Actualmente, una población de alces tiene un promedio de 2000 alces, y ese promedio ha ido creciendo 4% cada año. Debido a la fluctuación estacional, la población oscila de 50 por debajo del promedio en el invierno hasta 50 por encima de la media en el verano. Encuentra una función que modele el número de alces después de$t$ años, comenzando en el invierno.

Solución

Hay dos componentes en el comportamiento de la población de alces: el promedio cambiante y la oscilación. El promedio es un crecimiento exponencial, a partir del año 2000 y creciendo 4% cada año. Escribiendo una fórmula para esto:

\[average=initial(1+r)^{t} =2000(1+0.04)^{t}\nonumber\]

Para la oscilación, dado que la población oscila 50 por encima y por debajo de la media, la amplitud será de 50. Dado que la población tarda un año en ciclar, el periodo es de 1. Encontramos el valor del coeficiente de estiramiento horizontal\[B=\frac{\text{original period}}{\text{new period}}=\frac{2\pi }{1}=2\pi \nonumber\]

La función inicia en invierno, por lo que la forma de la función será un coseno negativo, ya que inicia en el valor más bajo.

Poniéndolo todo junto, la ecuación sería:

\[P(t)=-50\cos (2\pi {\kern 1pt} t)+midline\nonumber\]

Dado que la línea media representa la población promedio, sustituimos en la función exponencial en la ecuación poblacional para encontrar nuestra ecuación final:

\[P(t)=-50\cos (2\pi {\kern 1pt} t)+2000(1+0.04)^{t}\nonumber\]

Este es un ejemplo de cambio de línea media — en este caso una línea media exponencialmente cambiante.

CAMBIANDO MIDLINE

Una función de la forma$f(t)=A\sin (Bt)+g(t)$ oscilará por encima y por debajo del promedio dado por la función$g(t)$.

Cambio de línea media

El cambio de líneas medias puede ser exponencial, lineal o cualquier otro tipo de función. Aquí hay algunos ejemplos:

$Un gráfico que muestra una línea creciente en rojo discontinuo, con una función de estilo sinusoidal en azul que se muestra oscilando por encima y por debajo de esa línea, con período constante, y picos y valles a una distancia constante por encima y por debajo de la línea.$ $Un gráfico que muestra una curva exponencial creciente en rojo discontinuo, con una función de estilo sinusoidal en azul que se muestra oscilando por encima y por debajo de esa curva, con período constante, y picos y valles a una distancia constante por encima y por debajo de la curva.$ $Un gráfico que muestra una curva parabólica en forma de U en rojo discontinuo, con una función de estilo sinusoidal en azul que se muestra oscilando por encima y por debajo de esa curva, con período constante, y picos y valles a una distancia constante por encima y por debajo de la curva.$

Ejemplo$\PageIndex{2}$

Encuentra una función con línea media lineal de la forma$f(t)=A\sin \left(\dfrac{\pi }{2} t\right)+mt+b$ que pasará por los puntos que se indican a continuación.

$t$	0	1	2	3
$f(t)$	5	10	9	8

Ya que se nos da el valor del coeficiente de compresión horizontal podemos calcular el periodo de esta función: nuevo periodo =$\dfrac{\text{original period}}{B}$ =$\dfrac{2\pi}{\pi/2}$ = 4.

Solución

Dado que la función seno está en la línea media al inicio de un ciclo y a mitad de un ciclo, esperaríamos que esta función estuviera en la línea media en t = 0 y t = 2, ya que 2 es la mitad del periodo completo de 4. En base a esto, esperamos que los puntos (0, 5) y (2, 9) sean puntos en la línea media. Podemos ver claramente que esta no es una función constante y así usamos los dos puntos para calcular una función lineal:$midline=mt+b$. A partir de estos dos puntos podemos calcular una pendiente:

\[m=\dfrac{9-5}{2-0} =\dfrac{4}{2} =2\nonumber\]

Combinando esto con el valor inicial de 5, tenemos la línea media:$midline=2t+5$.

La función completa tendrá forma$f(t)=A\sin \left(\dfrac{\pi }{2} t\right)+2t+5$. Para encontrar la amplitud, podemos enchufar un punto que no hayamos usado ya, como (1, 10).

\[10=A\sin \left(\dfrac{\pi }{2} (1)\right)+2(1)+5\nonumber\]Evaluar el seno y combinar términos similares
\[10=A+7\nonumber\]
\[A=3\nonumber\]

Una función de la forma dada ajustando los datos sería

\[f(t)=3\sin \left(\dfrac{\pi }{2} t\right)+2t+5\nonumber\]

Observe que podríamos haber tomado un enfoque alternativo al enchufar los puntos (0, 5) y (2, 9) en la ecuación original. Sustituyendo (0, 5),

\[5=A\sin \left(\dfrac{\pi }{2} (0)\right)+m(0)+b\nonumber\]Evaluar el seno y simplificar
\[5=b\nonumber\]

Sustitución (2, 9)

\[9=A\sin \left(\dfrac{\pi }{2} (2)\right)+m(2)+5\nonumber\]Evaluar el seno y simplificar
\[9=2m+5\nonumber\]
\[4=2m\nonumber\]
\[m=2\nonumber\] como encontramos anteriormente. Ahora podemos proceder a encontrar de$A$ la misma manera que lo hacíamos antes.

Ejemplo$\PageIndex{3}$

El número de turistas que visitan una estación de esquí y senderismo tiene un promedio de 4000 personas al año y oscila estacionalmente, 1000 por encima y por debajo de la media. Debido a una campaña de comercialización, el número promedio de turistas ha ido aumentando en 200 cada año. Escribir una ecuación para el número de turistas después de$t$ años, comenzando en la temporada alta.

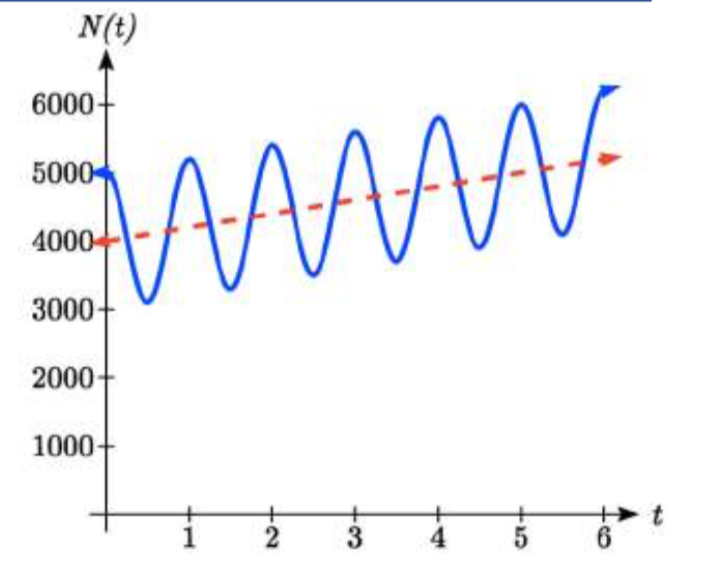
$Un gráfico que muestra una línea discontinua en rojo que comienza en 0 coma 4000 y pasa por 5 coma 5000. Una función de estilo sinusoidal se muestra en azul, con picos y valles grapando una amplitud constante por encima y por debajo de la línea. Comienza por encima de la línea roja en 0 coma 5000, disminuyendo por debajo de la línea, luego aumentando de nuevo hasta otro máximo en 1 coma 5200.$

Solución

Nuevamente hay dos componentes a este problema: la oscilación y la media. Para la oscilación, el número de turistas oscila 1000 por encima y por debajo de la media, dando una amplitud de 1000. Dado que la oscilación es estacional, tiene un periodo de 1 año. Dado que se nos da un punto de partida de “temporada alta”, modelaremos este escenario con una función coseno.

Hasta el momento, esto da una ecuación en la forma$N(t)=1000\cos (2\pi {\kern 1pt} t)+midline$.

El promedio es actualmente de 4000, y está aumentando en 200 cada año. Se trata de una tasa de cambio constante, por lo que se trata de un crecimiento lineal,$average=4000+200t$. Esta función actuará como la línea media.

Combinar estas dos piezas da una función para el número de turistas:

\[N(t)=1000\cos (2\pi {\kern 1pt} t)+4000+200t\nonumber\]

Ejercicio$\PageIndex{1}$

Dada la función$g(x)=(x^{2} -1)+8\cos (x)$, describir la línea media y la amplitud usando palabras.

Contestar: La línea media sigue la trayectoria de la cuadrática$x^{2} -1$ y la amplitud es un valor constante de 8.

Amplitud cambiante

También hay situaciones en las que la amplitud de una función sinusoidal no permanece constante. De vuelta en el Capítulo 6, modelamos el movimiento de un resorte usando una función sinusoidal, pero tuvimos que ignorar la fricción al hacerlo. Si hubiera fricción en el sistema, esperaríamos que la amplitud de la oscilación disminuyera con el tiempo. En la ecuación$f(t)=A\sin (Bt)+k$,$A$ da la amplitud de la oscilación, podemos permitir que la amplitud cambie reemplazando esta constante$A$ por una función$A(t)$.

AMPLITUIDAD

Una función de la forma$f(t)=A(t)\sin (Bt)+k$ oscilará por encima y por debajo de la línea media con una amplitud dada por$A(t)$.

Aquí hay algunos ejemplos:

$Una gráfica que muestra dos líneas discontinuas en rojo, una gráfica creciente y es igual a t, y una decreciente y es igual a t negativa, cruzando en el origen. Una función de estilo sinusoidal se muestra en azul, con período constante, línea media a 0 y amplitud cambiando de manera que los picos y valles tocan las dos líneas discontinuas.$ $Una gráfica que muestra dos curvas discontinuas en rojo, una gráfica exponencial ascendente cóncava creciente y su reflexión vertical. Una función de estilo sinusoidal se muestra en azul, con período constante, línea media a 0 y amplitud cambiando para que los picos y valles toquen las dos curvas discontinuas.$ $Una gráfica que muestra dos curvas discontinuas en rojo, una gráfica parabólica en forma de U de apertura hacia arriba de y es igual a x cuadrado, y es reflexión vertical. Una función de estilo sinusoidal se muestra en azul, con período constante, línea media a 0 y amplitud cambiando para que los picos y valles toquen las dos curvas discontinuas.$

Al pensar en un resorte con amplitud decreciente con el tiempo, es tentador usar la herramienta más simple para el trabajo: una función de $Una gráfica de estilo sinusoidal con periodo constante y línea media a 0, que comienza con una amplitud de 10 que disminuye linealmente a una amplitud de 0 cuando t es igual a 10. La amplitud entonces aumenta linealmente.$ oreja lin. Pero si intentamos modelar la amplitud con una función lineal decreciente, tal como$A(t)=10-t$, vemos rápidamente el problema cuando graficamos la ecuación$f(t)=(10-t)\sin (4t)$.

Mientras que la amplitud disminuye al principio como se pretendía, la amplitud alcanza cero en$t = 10$, luego continúa más allá de la intercepción, aumentando en valor absoluto, que no es el comportamiento esperado. Este comportamiento y función pueden modelar la situación en un dominio restringido y podríamos intentar atribuir el resto al desglose del modelo, pero de hecho los resortes simplemente no se comportan así.

$Una gráfica de estilo sinusoidal con período constante y línea media a 0, que comienza con una amplitud de 10 que disminuye exponencialmente, acercándose a 0 a medida que t se acerca al infinito.$

Un mejor modelo, como aprenderás más adelante en física y cálculo, mostraría la amplitud decreciente en un porcentaje fijo cada segundo, conduciendo a un modelo de decaimiento exponencial para la amplitud.

MOVIMIENTO ARMÓNICO

El movimiento armónico amortiguado, exhibido por resortes sujetos a fricción, sigue un modelo de la forma

\[f(t)=ab^{t} \sin (Bt)+k\text{ or }f(t)=ae^{rt} \sin (Bt)+k\nonumber\]

Ejemplo$\PageIndex{4}$

Un resorte con longitud natural de pies pulgadas se tira hacia atrás 6 pies y se libera. Oscila una vez cada 2 segundos. Su amplitud disminuye un 20% cada segundo. Encuentre una función que modele la posición del resorte t segundos después de haber sido liberado.

Solución

Dado que el resorte oscilará a ambos lados de la longitud natural, la línea media estará a 20 pies. La oscilación tiene un periodo de 2 segundos, y así lo es el coeficiente de compresión horizontal$B=\pi$. Adicionalmente, comienza a la distancia más alejada de la pared, indicando un modelo coseno.

$Una gráfica de estilo sinusoidal que alcanza un pico a t es igual a 0, 2, 4, etc. La gráfica oscila por encima y por debajo de una línea media de y es igual a 20. La gráfica comienza en 0 coma 26, disminuye hasta 1 coma aproximadamente 15, aumenta a 2 comas aproximadamente 24, disminuye a 3 coma 17, y continúa oscilando con amplitud decreciente.$ En tanto, la amplitud comienza en 6 pies, y disminuye en 20% cada segundo, dando una función de amplitud de$A(t)=6(1-0.20)^{t}$.

Combinando esto con la información sinusoidal da una función para la posición del resorte:

\[f(t)=6(0.80)^{t} \cos (\pi {\kern 1pt} t)+20\nonumber\]

Ejemplo$\PageIndex{5}$

Un resorte con longitud natural de 30 cm se saca 10 cm y se libera. Oscila 4 veces por segundo. Después de 2 segundos, la amplitud ha disminuido a 5 cm. Encuentra una función que modele la posición del muelle.

Solución

La oscilación tiene un periodo de$\dfrac{1}{4}$ segundo, entonces$B = \dfrac{2\pi}{1/4} = 8\pi$. Dado que el resorte oscilará a ambos lados de la longitud natural, la línea media estará a 30 cm. Comienza a la distancia más alejada de la pared, sugiriendo un modelo coseno. Juntos, esto da

\[f(t)=A(t)\cos (8\pi {\kern 1pt} t)+30.\nonumber\]

Para la función de amplitud, notamos que la amplitud comienza en 10 cm, y disminuye a 5 cm después de 2 segundos. Esto da dos puntos (0, 10) y (2, 5) que deben ser satisfechos por una función exponencial:$A(0)=10$ y$A(2)=5$. Dado que la función es exponencial, podemos usar la forma$A(t)=ab^{t}$. Sustituyendo el primer punto,$10=ab^{0}$, entonces$a = 10$. Sustituyendo en el segundo punto,

\[5=10b^{2}\nonumber\]Dividir por 10
\[\dfrac{1}{2} =b^{2}\nonumber\] Toma la raíz cuadrada
\[b=\sqrt{\dfrac{1}{2} } \approx 0.707\nonumber\]

Esto da una función de amplitud de$A(t)=10(0.707)^{t}$. Combinando esto con la oscilación,

\[f(t)=10(0.707)^{t} \cos (8\pi t)+30\nonumber\]

Ejercicio$\PageIndex{2}$

Cierta acción comenzó con un valor alto de $7 por acción, oscilando mensualmente por encima y por debajo del valor promedio, con la oscilación disminuyendo 2% anual. No obstante, el valor promedio comenzó en 4 dólares por acción y ha crecido linealmente 50 centavos al año.

a. Encuentra una fórmula para la línea media y la amplitud.
b. Encontrar una función$S(t)$ que modele el valor de la acción después de$t$ años.

Contestar: \[\begin{array}{l} {m(t)=4+0.5t} \\ {A(t)=7(0.98)^{t} } \end{array}\nonumber\]
\[S(t)= 7(0.98)^{t} \cos \left(24\pi t\right)+4+0.5t\nonumber\]

Ejemplo$\PageIndex{6}$

En la radio AM (Amplitud Modulada), se utiliza una onda portadora con alta frecuencia para transmitir música u otras señales aplicando la señal a transmitir como la amplitud de la señal portadora. Una nota musical con frecuencia 110 Hz (Hertz = ciclos por segundo) debe ser transportada sobre una onda con frecuencia de 2 kHz (kiloHertz = miles de ciclos por segundo). Si la onda musical tiene una amplitud de 3, escriba una función que describa la onda de difusión.

Solución

La onda portadora, con una frecuencia de 2000 ciclos por segundo, tendría periodo$\dfrac{1}{2000}$ de un segundo, dando una ecuación de la forma$\sin (4000\pi {\kern 1pt} t)$. Nuestra elección de una función sinusoidal aquí fue arbitraria — hubiera funcionado simplemente estaba bien usar un coseno.

El tono musical, con una frecuencia de 110 ciclos por segundo, tendría un periodo$\dfrac{1}{110}$ de segundo. Con una amplitud de 3, esto correspondería a una función de la forma$3\sin (220\pi {\kern 1pt} t)$. Nuevamente nuestra elección de usar una función sinusoidal es arbitraria.

La onda musical está actuando como la amplitud de la onda portadora, por lo que multiplicaremos la función del tono musical por la función de onda portadora, resultando en la función

\[f(t)=3\sin (220\pi {\kern 1pt} t)\sin (4000\pi {\kern 1pt} t)\nonumber\]

$Se muestran tres ciclos de una gráfica sinusoidal discontinua en rojo, con un periodo de 1 sobre 110. Una curva de estilo sinusoidal de frecuencia mucho mayor se muestra en azul, con un periodo de 1 sobre 2000, con una línea media a 0, y los picos y valles de la curva tocando la curva sinusoidal discontinua y su reflexión vertical.$

Temas Importantes de esta Sección

Cambio de línea media
Amplitud cambiante
Cambios Lineales
Cambios exponenciales
Movimiento armónico amortiguado

Search

Text Color

Text Size

Margin Size

Font Type

\(t\)	0	1	2	3
\(f(t)\)	5	10	9	8