7.4.4E: Modelado de Amplitud Cambiante y Línea Media (Ejercicios)

Última actualización
Guardar como PDF

Page ID: 116652

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Sección 7.4 Ejercicios

Encuentre una posible fórmula para la función trigonométrica cuyos valores se dan en las siguientes tablas.

$x$	0	3	6	9	12	15	18
$y$	-4	-1	2	-1	-4	-1	2

$x$	0	2	4	6	8	10	12
$y$	5	1	-3	1	5	1	-3

3. El desplazamiento$h(t)$, en centímetros, de una masa suspendida por un resorte es modelado por la función$h\left(t\right)=8{\rm sin}(6\pi t)$, donde t se mide en segundos. Encuentra la amplitud, periodo y frecuencia de este desplazamiento.

4. El desplazamiento$h(t)$, en centímetros, de una masa suspendida por un resorte es modelado por la función$h\left(t\right)=11{\rm sin}(12\pi t)$, donde$t$ se mide en segundos. Encuentra la amplitud, periodo y frecuencia de este desplazamiento.

5. Una población de conejos oscila 19 por encima y por debajo del promedio durante el año, alcanzando el valor más bajo en enero. La población promedio comienza en 650 conejos y aumenta 160 cada año. Encontrar una función que modele la población,$P$, en términos de los meses transcurridos desde enero,$t$.

6. Una población de venados oscila 15 por encima y por debajo del promedio durante el año, alcanzando el valor más bajo en enero. La población promedio comienza en 800 venados y aumenta en 110 cada año. Encontrar una función que modele la población,$P$, en términos de los meses transcurridos desde enero,$t$.

7. Una población de cratas almizcleras oscila 33 por encima y por debajo del promedio durante el año, alcanzando el valor más bajo en enero. La población promedio inicia en 900 cratas almizcleras y aumenta 7% cada mes. Encontrar una función que modele la población,$P$, en términos de los meses transcurridos desde enero,$t$.

8. Una población de peces oscila 40 por encima y por debajo del promedio durante el año, alcanzando el valor más bajo en enero. La población promedio comienza en 800 peces y aumenta 4% cada mes. Encontrar una función que modele la población,$P$, en términos de los meses transcurridos desde enero,$t$.

9. Se fija un resorte al techo y se tira 10 cm hacia abajo del equilibrio y se libera. La amplitud disminuye 15% cada segundo. El resorte oscila 18 veces cada segundo. Encuentra una función que modele la distancia,$D$, el extremo del resorte está por debajo del equilibrio en términos de segundos,$t$, ya que el resorte fue liberado.

10. Se fija un resorte al techo y se tira 7 cm hacia abajo del equilibrio y se libera. La amplitud disminuye 11% cada segundo. El resorte oscila 20 veces cada segundo. Encuentra una función que modele la distancia,$D$, el extremo del resorte está por debajo del equilibrio en términos de segundos,$t$, ya que el resorte fue liberado.

11. Se fija un resorte al techo y se tira 17 cm hacia abajo del equilibrio y se libera. Después de 3 segundos la amplitud ha disminuido a 13 cm. El resorte oscila 14 veces cada segundo. Encuentra una función que modele la distancia,$D$ el extremo del resorte está por debajo del equilibrio en términos de segundos,$t$, ya que el resorte fue liberado.

12. Un resorte se une al techo y se tira 19 cm hacia abajo del equilibrio y se libera. Después de 4 segundos la amplitud ha disminuido a 14 cm. El resorte oscila 13 veces cada segundo. Encuentra una función que modele la distancia,$D$ el extremo del resorte está por debajo del equilibrio en términos de segundos,$t$, ya que el resorte fue liberado.

Coincide cada forma de ecuación con una de las gráficas.

13. a.$ab^{x} +\sin \left(5x\right)$
b.$\sin \left(5x\right)+mx+b$

14. a.$ab^{x} \sin \left(5x\right)$
b.$\left(mx+b\right){\rm sin}(5x)$

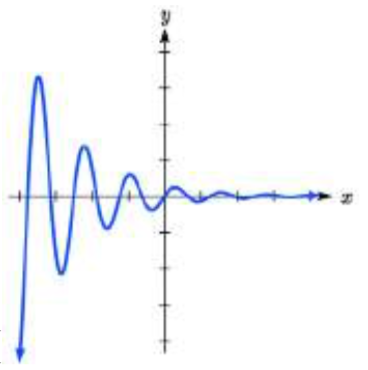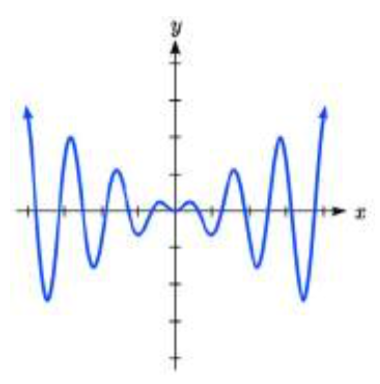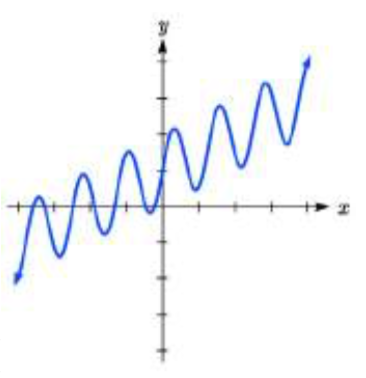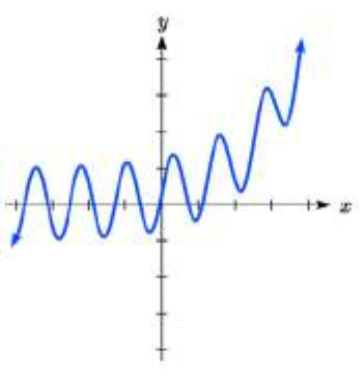
I $2019-07-19 8.2.23.png$ II $2019-07-19 8.02.50.png$ III $2019-07-19 8.03.17.png$ IV $2019-07-19 8.04.00.png$

Encuentra una función del formulario$y=ab^{x} +c\sin \left(\dfrac{\pi }{2} x\right)$ que se ajuste a los datos dados.

15.

$x$	0	1	2	3
$y$	6	29	96	379

16.

$x$	0	1	2	3
$y$	6	34	150	746

Encuentra una función del formulario$y=a\sin \left(\dfrac{\pi }{2} x\right)+m+bx$ que se ajuste a los datos dados.

17.

$x$	0	1	2	3
$y$	7	6	11	16

18.

$x$	0	1	2	3
$y$	-2	6	4	2

Encuentra una función del formulario$y=ab^{x} \cos \left(\dfrac{\pi }{2} x\right)+c$ que se ajuste a los datos dados.

19.

$x$	0	1	2	3
$y$	11	3	1	3

20.

$x$	0	1	2	3
$y$	4	1	-11	1

Contestar

1. $y = 3\sin(\dfrac{\pi}{6} (x - 3)) - 1$

3. Amplitud: 8, Periodo:$\dfrac{1}{3}$ segundo, Frecuencia: 3 Hz (ciclos por segundo)

5. $P(t) = -19\cos(\dfrac{\pi}{6}t) + \dfrac{40}{3} t + 650$

7. $P(t) = -33\cos(\dfrac{\pi}{6}t) + 900(1.07)^t$

9. $D(t) = 10 (0.85)^t \cos(36 \pi t)$

11. $D(t) = 17(0.9145)^t \cos(28\pi t)$

13. a. IV
b. III

15. $y = 6(4)^x + 5 \sin(\dfrac{\pi}{2} x)$

17. $y = -3\sin(\dfrac{\pi}{2}) + 2x + 7$

19. $y = 8(\dfrac{1}{2})^x \cos(\dfrac{\pi}{2}x) + 3$

\(x\)	0	3	6	9	12	15	18
\(y\)	-4	-1	2	-1	-4	-1	2

\(x\)	0	2	4	6	8	10	12
\(y\)	5	1	-3	1	5	1	-3

\(x\)	0	1	2	3
\(y\)	6	29	96	379

\(x\)	0	1	2	3
\(y\)	6	34	150	746