8.2: Coordenadas polares

Última actualización
Guardar como PDF

Page ID: 116884

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

El sistema de coordenadas con el que estamos más familiarizados se llama sistema de coordenadas cartesianas, un plano rectangular dividido en cuatro cuadrantes por ejes horizontales y verticales.

$Una rejilla de coordenadas rectangular vacía, con líneas de rejilla horizontales y verticales.$ En capítulos anteriores, a menudo encontramos las coordenadas cartesianas de un punto en un círculo en un ángulo dado desde el eje horizontal positivo. A veces ese ángulo, junto con la distancia del punto desde el origen, proporciona una manera más útil de describir la ubicación del punto que las coordenadas cartesianas convencionales.

Coordenadas polares

Las coordenadas polares de un punto consisten en un par ordenado, ($r$,$\theta$), donde$r$ está la distancia desde el punto hasta el origen, y$\theta$ es el ángulo medido en posición estándar.

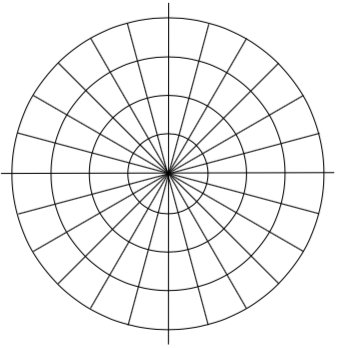
$Una cuadrícula gráfica polar vacía, con círculos concéntricos centrados en el origen, y rayos dibujados desde el origen en ángulos incrementales.$

Observe que si tuviéramos que “cuadrícular” el plano para coordenadas polares, se vería como la gráfica a la derecha, con círculos en radios incrementales, y rayos dibujados en ángulos incrementales.

Ejemplo$\PageIndex{1}$

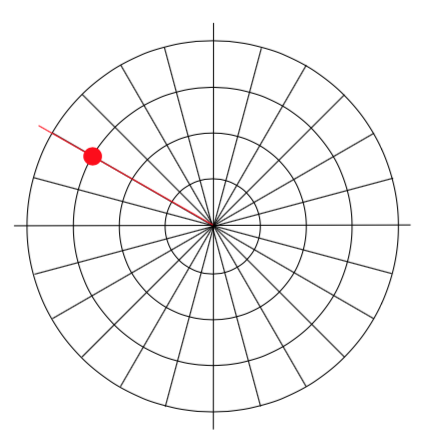
Trazar el punto polar ($3, \dfrac{5\pi}{6}$).

Solución

Este punto estará a una distancia de 3 desde el origen, en un ángulo de$\dfrac{5\pi}{6}$. Ploteando esto

$Una rejilla polar, con un punto A en el primer cuadrante$

Ejemplo$\PageIndex{2}$

Trazar el punto polar ($-2, \dfrac{\pi}{4}$).

Solución

Normalmente usamos$r$ valores positivos, pero ocasionalmente nos encontramos con casos en los que$r$ es negativo. En una recta numérica regular, medimos valores positivos a la derecha y valores negativos a la izquierda. Trazaremos este punto de manera similar. Para comenzar, giramos a un ángulo de$\dfrac{\pi}{4}$.

Mover esta dirección, hacia el primer cuadrante, serían valores r positivos. Para valores r negativos, nos movemos en dirección opuesta, hacia el tercer cuadrante. Al trazar esto:

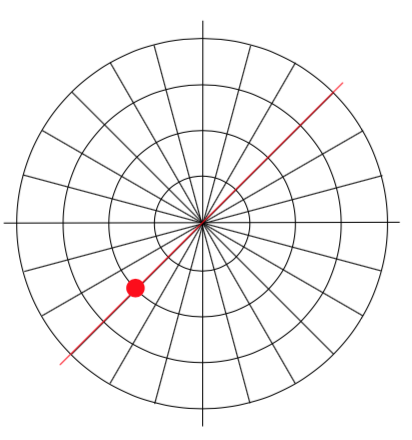
$En una rejilla polar, se muestra una línea en un ángulo de pi sobre 4, con un punto indicado en la línea en el tercer cuadrante a una distancia de 2 desde el origen.$

Tenga en cuenta que el punto resultante es el mismo que el punto polar ($2, \dfrac{5\pi}{4}$). De hecho, cualquier punto cartesiano puede ser representado por un número infinito de diferentes coordenadas polares sumando o restando rotaciones completas a estos puntos. Por ejemplo, el mismo punto también podría representarse como ($2, \dfrac{13\pi}{4}$).

Ejercicio$\PageIndex{1}$

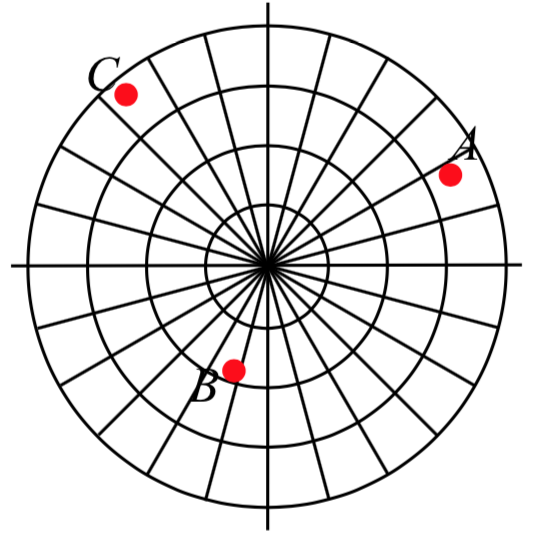
Trace los siguientes puntos dados en coordenadas polares y etiquételos.

a.$A = (3, \dfrac{\pi}{6})$

b.$B = (-2, \dfrac{\pi}{3})$

c.$C = (4, \dfrac{3\pi}{4})$

Responder: $Una rejilla polar. El punto A está en el radio 3 círculo en ángulo pi sobre 6 en el primer cuadrante. El punto B está en el círculo de radio 2 en el tercer cuadrante en ángulo 4 pi sobre 3. El punto C está en el radio 4 círculo en el segundo cuadrante en ángulo 3 pi sobre 4.$

Conversión de puntos

Para convertir entre coordenadas polares y coordenadas cartesianas, recordamos las relaciones que desarrollamos en el Capítulo 5.

Conversión entre coordenadas polares y cartesianas

Para convertir entre coordenadas polares ($r, \theta$) y cartesianas ($x, y$), utilizamos las relaciones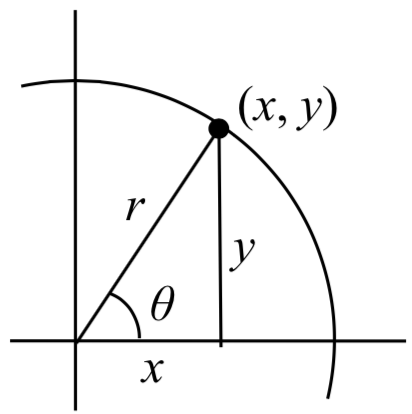 $Un círculo centrado en el origen con una línea etiquetada r dibujada en un ángulo de theta. El punto donde la línea se encuentra con el círculo se etiqueta x coma y. Una línea vertical se dibuja desde ese punto hasta el eje x formando un triángulo, con la longitud vertical etiquetada y. La pata horizontal del triángulo desde el origen hasta la línea vertical se etiqueta x.$

\[\cos (\theta )=\frac{x}{r}\quad x=r\cos (\theta )\]

\[\sin (\theta )=\frac{y}{r}\quad y=r\sin (\theta )\]

\[\tan (\theta )=\frac{y}{x}\quad x^{2}+y^{2}=r^{2}\]

A partir de esta relación y nuestro conocimiento del círculo unitario, si$r = 1$ y$\theta = \dfrac{\pi}{3}$, las coordenadas polares serían$(r, \theta) = (1, \dfrac{\pi}{3})$, y las coordenadas cartesianas correspondientes$(x, y) = (\dfrac{1}{2}, \dfrac{\sqrt{3}}{2})$.

Recordar los valores de tu círculo unitario será muy útil a medida que conviertas entre coordenadas cartesianas y polares.

Ejemplo$\PageIndex{3}$

Encuentra las coordenadas cartesianas de un punto con coordenadas polares$(r, \theta) = (5, \dfrac{2\pi}{3})$.

Solución

Para encontrar las$y$ coordenadas$x$ y del punto,

\[x = r\text{cos} (\theta) = 5 \cos (\dfrac{2\pi}{3}) = 5(-\dfrac{1}{2}) = -\dfrac{5}{2}\nonumber\]

\[y = r\text{sin} (\theta) = 5 \sin (\dfrac{2\pi}{3}) = 5(-\dfrac{\sqrt{3}}{2}) = -\dfrac{5\sqrt{3}}{2}\nonumber\]

Las coordenadas cartesianas son ($-\dfrac{5}{2}, \dfrac{5\sqrt{3}}{2}$).

Ejemplo$\PageIndex{4}$

Encuentra las coordenadas polares del punto con coordenadas cartesianas (−3, −4).

Solución

Comenzamos por encontrar la distancia$r$ usando la relación pitagórica$x^2 + y^2 = r^2$

\[(-3)^2 + (-4)^2 = r^2\nonumber\]
\[9 + 16 = r^2\nonumber\]
\[r^2 = 25\nonumber\]
\[r = 5\nonumber\]

Ahora que conocemos el radio, podemos encontrar el ángulo usando cualquiera de las tres relaciones trigonométricas. Tenga en cuenta que cualquiera de las relaciones producirá dos soluciones en el círculo, y necesitamos considerar el cuadrante para determinar qué solución aceptar. Usando el coseno, por ejemplo:

\[\cos(\theta) = \dfrac{x}{r} = \dfrac{-3}{5}\nonumber\]
\[\theta = \cos^{-1}(\dfrac{-3}{5}) \approx 2.214\nonumber\]Por simetría, hay una segunda posibilidad en
\[\theta = 2\pi - 2.24 = 4.069\nonumber\]

Dado que el punto (-3, -4) se encuentra en el$3^{\text{rd}}$ cuadrante, podemos determinar que el segundo ángulo es el que necesitamos. Las coordenadas polares de este punto son$(r, \theta) = (5, 4.069)$.

Ejercicio$\PageIndex{2}$

Convertir lo siguiente.

a. Convertir coordenadas polares$(r, \theta) = (2, \pi)$ a ($x, y)$.

b. Convertir coordenadas cartesianas$(x, y) = (0, -4)$ a$(r, \theta)$.

Responder

a.$(r, \theta) = (2, \pi)$ convierte a$(x, y) = (2\cos(\pi), 2\sin(\pi)) = (-2, 0)$

b.$(x, y) = (0, -4)$ convierte a$(r, \theta) = (4, \dfrac{3\pi}{2})\ or\ (-4, \dfrac{\pi}{2})$

Ecuaciones Polares

Así como una ecuación cartesiana como$y = x^2$ describe una relación entre$x$ y$y$ valores en una cuadrícula cartesiana, se puede escribir una ecuación polar describiendo una relación entre$r$ y$\theta$ valores en la cuadrícula polar.

Ejemplo$\PageIndex{5}$

Esbozar una gráfica de la ecuación polar$r = \theta$.

Solución

La ecuación$r = \theta$ describe todos los puntos para los que el radio$r$ es igual al ángulo. Para visualizar esta relación, podemos crear una tabla de valores.

$\theta$	0	$\pi/4$	$\pi/2$	$3\pi/4$	$\pi$	$5\pi/4$	$3\pi/2$	$7\pi/4$	$2\pi$
$r$	0	$\pi/4$	$\pi/2$	$3\pi/4$	$\pi$	$5\pi/4$	$3\pi/2$	$7\pi/4$	$2\pi$

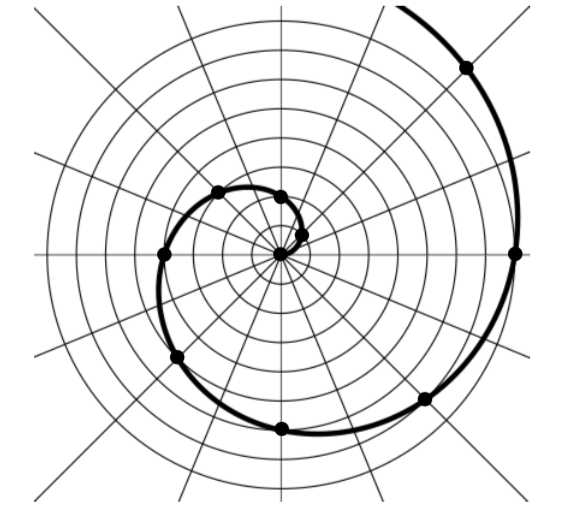
$En una cuadrícula polar, una gráfica que sale en espiral desde el origen. En un ángulo de pi sobre 4 hay un punto a una distancia pi sobre 4 desde el origen. En un ángulo de pi sobre 2 hay un punto a una distancia pi sobre 2 desde el origen, y así sucesivamente.$

Podemos trazar estos puntos en el plano, y luego esbozar una curva que se ajuste a los puntos. El gráfico resultante es una espiral.

Observe que la gráfica resultante no puede ser el resultado de una función de la forma$y = f(x)$, ya que no pasa la prueba de línea vertical, a pesar de que resultó de una función dando$r$ en términos de$\theta$.

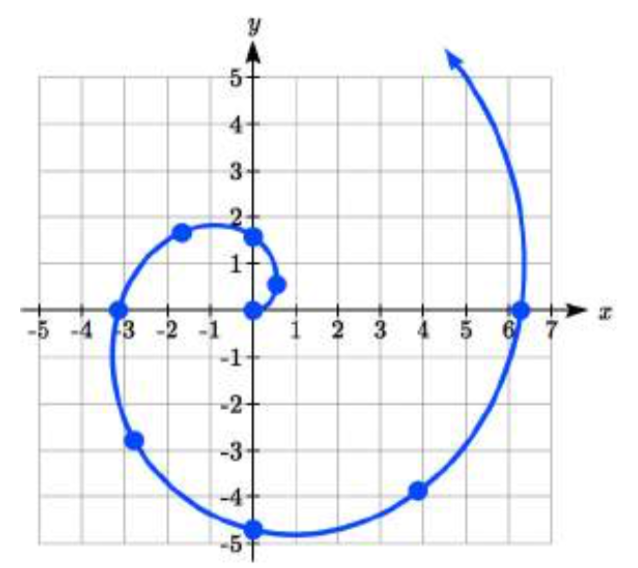
$Un gráfico en espiral que se muestra en una cuadrícula cartesiana. La gráfica sale en espiral desde el origen, pasando por estos puntos aproximados: 0 coma 0, 0.5 coma 0.5, 0 coma 1.6, negativo 1.6 coma 1.6, negativo pi coma 0, negativo 2.9 coma neativo 2.9, 0 coma negativo 4.8.$

Si bien es agradable ver ecuaciones polares en cuadrículas polares, es más común que las gráficas polares se grafiquen en el sistema de coordenadas cartesianas, y así, el resto de las ecuaciones polares se graficarán en consecuencia.

Aquí se muestra el gráfico espiral de arriba en una cuadrícula cartesiana.

Ejemplo$\PageIndex{6}$

Esbozar una gráfica de la ecuación polar$r = 3$.

Solución

Recordemos que cuando una variable no aparece en la ecuación, es decir que no importa qué valor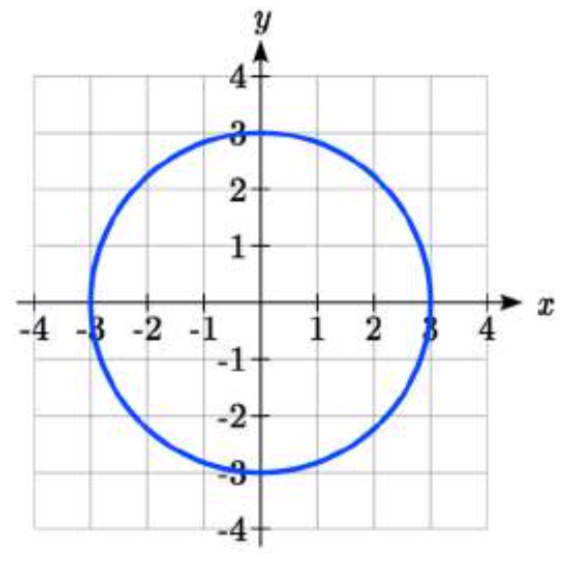 $Un círculo con radio 3 centrado en el origen.$ tenga esa variable; la salida para la ecuación seguirá siendo la misma. Por ejemplo, la ecuación cartesiana$y = 3$ describe todos los puntos donde$y = 3$, sin importar cuáles sean los valores x, se produce una línea horizontal.

De igual manera, esta ecuación polar está describiendo todos los puntos a una distancia de 3 del origen, sin importar cuál sea el ángulo, produciendo la gráfica de un círculo.

Los ajustes normales en calculadoras gráficas y gráfico de software en el sistema de coordenadas cartesianas con$y$ ser una función de$x$, donde la utilidad gráfica pide$f(x)$, o simplemente$y =$.

Para graficar ecuaciones polares, es posible que tengas que cambiar el modo de tu calculadora a Polar. Sabrás que has tenido éxito en cambiar el modo si ahora tienes$r$ como función de$\theta$, donde la utilidad gráfica pide$r(\theta)$, o simplemente$r =$.

Ejemplo$\PageIndex{7}$

Dibuje una gráfica de la ecuación$r = 4 \cos(\theta)$ polar y encuentre un intervalo en el que complete un ciclo.

Solución

Si bien podríamos volver a crear una tabla, trazar los puntos correspondientes y conectar los puntos, también podemos recurrir a la tecnología para graficarla directamente. Utilizando la tecnología, producimos la gráfica que se muestra aquí, un círculo que pasa por el origen.

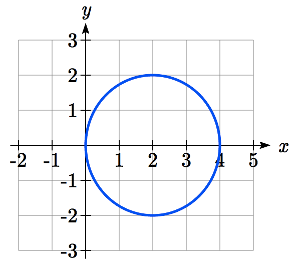
$Un círculo con radio 2, centrado en 2 coma 0. La gráfica toca los puntos 0 coma 0 y 4 coma 0.$

Dado que esta gráfica parece cerrar un bucle y repetirse, podríamos preguntar qué intervalo de$\theta$ valores arroja toda la gráfica. En$\theta = 0$,$r = 4\cos(0) = 4$, cediendo el punto (4, 0). Queremos el siguiente$\theta$ valor cuando la gráfica regrese al punto (4, 0). Resolver para cuando$x = 4$ equivale a resolver$r\cos(\theta) = 4$.

\[r \cos(\theta) = 4\nonumber\]Sustituir la ecuación por$r$ da
\[4\cos(\theta)\cos(\theta) = 4\nonumber\] Dividir por 4 y simplificar
\[\cos^{2}(\theta)= 1\nonumber\] Esto tiene soluciones a la hora de
\[\cos(\theta) = 1\text{ or }\cos(\theta) = -1\nonumber\] Resolver estos da soluciones
\[\theta = 0\text{ or }\theta = \pi\nonumber\]

Esto nos muestra a 0 radianes estamos en el punto (0, 4), y nuevamente en$\pi$ radianes estamos en el punto (0, 4) habiendo terminado una revolución completa.

Este intervalo$0 \le \theta < \pi$ produce una iteración completa del círculo.

Ejercicio$\PageIndex{3}$

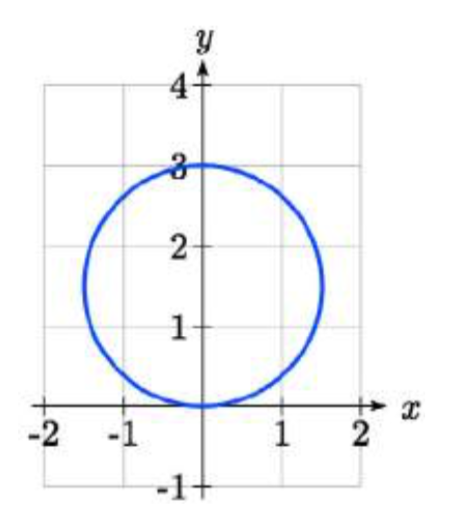
Dibuje una gráfica de la ecuación$r = 3 \sin (\theta)$ polar y encuentre un intervalo en el que complete un ciclo.

Responder

\[3 \sin(\theta) = 0\text{ at }\theta = 0\text{ and }\theta = \pi\nonumber\]

Se completa un ciclo en el intervalo$0 \le \theta < \pi$.

$Un círculo con radio 1.5, centrado en 0 coma 1.5. El círculo toca el origen y el punto 0 coma 3.$

Los últimos ejemplos han sido todos círculos. A continuación, consideraremos otras dos ecuaciones polares “nombradas”, limaçons y rosas.

Ejemplo$\PageIndex{8}$

Esbozar una gráfica de la ecuación polar$r = 4\sin(\theta) + 2$. ¿Qué intervalo de$\theta$ valores corresponde al bucle interno?

Solución

Este tipo de gráfica se llama limaçon. 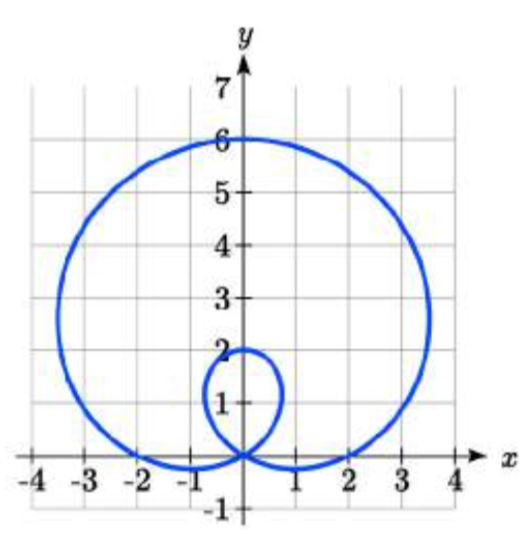$Una gráfica de un limacon. La gráfica tiene un bucle redondeado grande, comenzando en el origen, bajando luego aumentando a través de 2 coma 0, bucle hasta 0 coma 6, bucle a negativo 2 coma 0 y luego dando vueltas al origen. Luego, la gráfica continúa en un pequeño bucle que también comienza en el origen, recorre hasta 0 coma 2, luego vuelve al origen.$
Usando la tecnología, podemos dibujar la gráfica. El bucle interno comienza y termina en el origen, donde$r = 0$. Podemos resolver por los$\theta$ valores para los cuales$r = 0$.

\[0 = 4\sin(\theta) + 2\nonumber\]
\[-2 = 4\sin(\theta)\nonumber\]
\[\sin(\theta) = -\dfrac{1}{2}\nonumber\]
\[\theta = \dfrac{7\pi}{6}\text{ or }\theta = \dfrac{11\pi}{6}\nonumber\]

Esto nos dice que$r = 0$, así la gráfica pasa por el origen, dos veces en el intervalo$[0, 2\pi)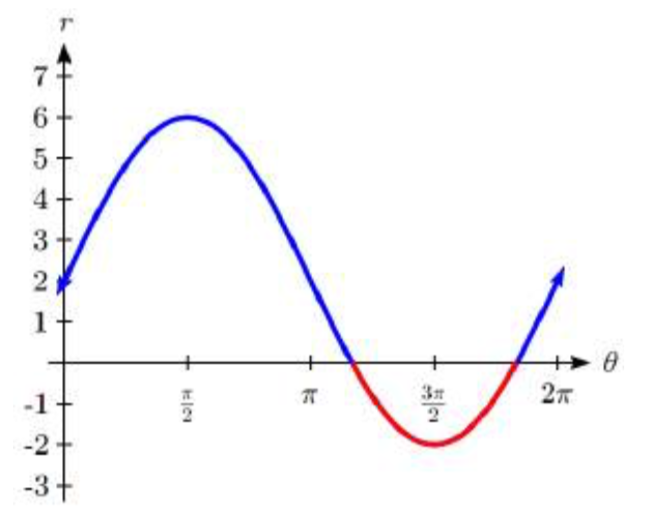$. $El eje horizontal se etiqueta theta y el eje vertical etiquetado r. Un gráfico sinusoidal, comenzando en la línea media en 0 coma 2, aumentando hasta pi sobre 2 coma 6, disminuyendo hasta 3 pi sobre 2 coma negativa 2, luego aumentando de nuevo hasta 2 pi coma 2. La parte de la gráfica que tiene una salida negativa se resalta en rojo$

El bucle interno surge del intervalo$\dfrac{7\pi}{6} \le \theta \le \dfrac{11\pi}{6}$.

Esto corresponde a donde la función$r = 4 \sin(\theta) + 2$ toma valores negativos, como podríamos ver si graficáramos la función en el$r \theta$ plano.

Ejemplo$\PageIndex{9}$

Esbozar una gráfica de la ecuación polar$r = \cos(3\theta)$. ¿Qué intervalo de$\theta$ valores describe un pequeño bucle de la gráfica?

Solución

Este tipo de gráfica se llama rosa de 3 hojas. 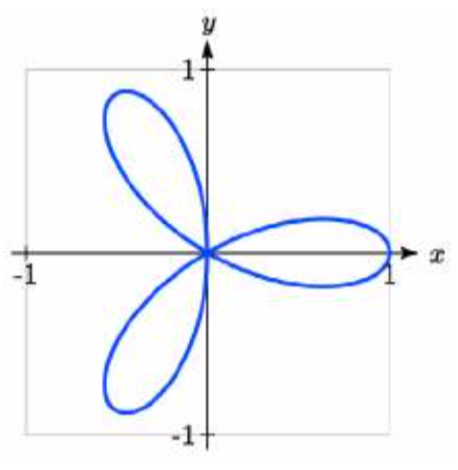$Gráfica de una rosa de 3 hojas. La gráfica consta de 3 bucles, todos tocando el origen. El primer bucle está más alejado del origen en 1 coma 0. El segundo está más alejado en negativo media coma raíz cuadrada de 3 sobre 2. El tercero está más alejado en una media coma negativa raíz cuadrada negativa de 3 sobre 2.$

Podemos utilizar la tecnología para producir una gráfica. El intervalo$[0, \pi)$ produce un ciclo de esta función. Al igual que con el último problema, podemos señalar que hay un intervalo en el que un bucle de esta gráfica comienza y termina en el origen, dónde$r = 0$. Resolviendo para$\theta$,

\[0 = \cos(3\theta)\nonumber\]Sustituto$u = 3\theta$
\[0 = \cos(u)\nonumber\]
\[u = \dfrac{\pi}{2}\text{ or }u = \dfrac{3\pi}{2}\text{ or }u = \dfrac{5\pi}{2}\nonumber\]

Deshacer la sustitución,

\[3 \theta = \dfrac{\pi}{2}\text{ or }3 \theta = \dfrac{3\pi}{2}\text{ or }3 \theta = \dfrac{5\pi}{2}\nonumber\]

\[\theta = \dfrac{\pi}{6}\text{ or }\theta = \dfrac{\pi}{2}\text{ or }\theta = \dfrac{5\pi}{6}\nonumber\]

Hay 3 soluciones sobre las$0 \le \theta < \pi$ que corresponden a las 3 veces que la gráfica regresa al origen, pero las dos primeras soluciones que resolvimos anteriormente son suficientes para concluir que

un bucle corresponde al intervalo$\dfrac{\pi}{6} \le \theta < \dfrac{\pi}{2}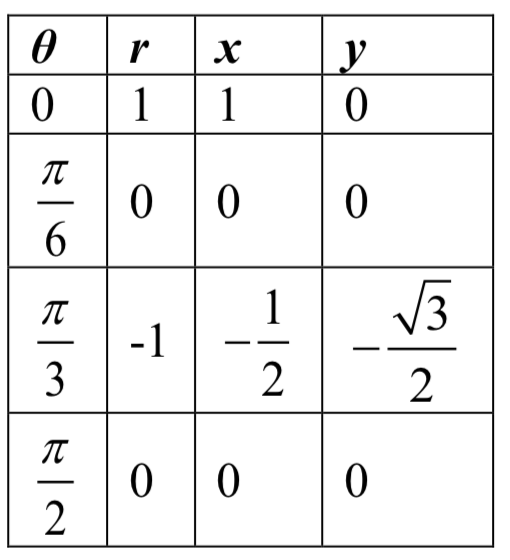$. $2019-07-21 7.54.40.png$

Si quisiéramos hacernos una idea de cómo la computadora dibujó esta gráfica, considere cuándo$\theta = 0$.

$r = \cos(3\theta) = \cos(0) = 1$, por lo que la gráfica comienza en (1, 0). Como encontramos anteriormente, en$\theta = \dfrac{\pi}{6}$ y$\theta = \dfrac{\pi}{2}$, la gráfica está en el origen. Al observar la ecuación, observe que cualquier ángulo intermedio$\dfrac{\pi}{6}$ y$\dfrac{\pi}{2}$, por ejemplo, en$\theta = \dfrac{\pi}{3}$, produce un negativo$r$:\[r = \cos(3 \cdot \dfrac{\pi}{3}) = \cos(\pi) = -1\nonumber\]

Observe que con un$r$ valor negativo y un ángulo con lado terminal en el primer cuadrante, el punto cartesiano correspondiente estaría en el tercer cuadrante. Dado que$r = \cos(3\theta)$ es negativo on$\dfrac{\pi}{6} \le \theta < \dfrac{\pi}{2}$, este intervalo corresponde al bucle de la gráfica en el tercer cuadrante.

Ejercicio$\PageIndex{4}$

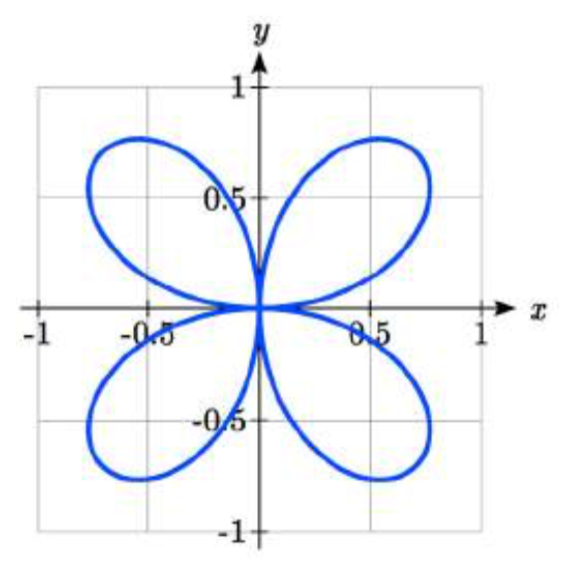
Esbozar una gráfica de la ecuación polar$r = \sin(2\theta)$. ¿Llamarías a esta función un limaçon o una rosa?

Responder

Se trata de una rosa de 4 hojas.

$Una gráfica de una rosa de 4 hojas, que consta de 4 bucles, todos tocando el origen. El primer bucle está más alejado del origen en la raíz cuadrada de 2 comas raíz cuadrada de 2, y las otras 3 hojas son reflejos de esa a través de los ejes y el origen.$

Conversión de ecuaciones

Si bien muchas ecuaciones polares no pueden expresarse bien en forma cartesiana (y viceversa), puede ser beneficioso convertir entre las dos formas, cuando sea posible. Para ello utilizamos las mismas relaciones que usamos para convertir puntos entre sistemas de coordenadas.

Ejemplo$\PageIndex{10}$

Reescribir la ecuación cartesiana$x^2 + y^2 = 6y$ como una ecuación polar.

Solución

Deseamos eliminar$x$ y$y$ de la ecuación e introducir$r$ y$\theta$. Idealmente, nos gustaría escribir la ecuación con$r$ aislado, si es posible, que representa$r$ como una función de$\theta$.

\[x^2 + y^2 = 6y\nonumber\]Recordando$x^2 + y^2 = r^2$ sustituimos
\[r^2 = 6y\nonumber\]$y = r\sin(\theta)$ y así sustituimos de nuevo
\[r^2 = 6r \sin(\theta)\nonumber\] Restar$6r\sin(\theta)$ de ambos lados
\[r^2 - 6r\sin(\theta) = 0\nonumber\] Factor
\[r (r - 6\sin(\theta)) = 0\nonumber\] Usa el teorema del factor cero
\[r = 6\sin(\theta)\text{ or }r = 0\nonumber\] Desde $r = 0$es sólo un punto, rechazamos esa solución.

La solución$r = 6\sin(\theta)$ es bastante similar a la que graficamos en el Ejemplo 7. De hecho, esta ecuación describe un círculo con la parte inferior en el origen y la parte superior en el punto (0, 6).

Ejemplo$\PageIndex{11}$

Reescribir la ecuación cartesiana$y = 3x + 2$ como una ecuación polar.

Solución

\[y = 3x + 2\nonumber\]Usar$y = r\sin(\theta)$ y$x = r\cos(\theta)$
\[r\sin(\theta) = 3r\cos(\theta) + 2\nonumber\] mover todos los términos con un
\[r\sin(\theta) - 3r\cos(\theta) = 2\nonumber\] factor$r$ a un lado$r$
\[r(\sin(\theta) - 3\cos(\theta)) = 2\nonumber\] Dividir
\[r = \dfrac{2}{\sin(\theta) - 3\cos(\theta)}\nonumber\]

En este caso, la ecuación polar es más difícil de manejar que la ecuación cartesiana, pero todavía hay momentos en los que esta ecuación podría ser útil.

Ejemplo$\PageIndex{12}$

Reescribir la ecuación polar$r = \dfrac{3}{1- 2\cos(\theta)}$ como una ecuación cartesiana.

Solución

Queremos eliminar$\theta$ y$r$ e introducir$x$ y$y$. Por lo general, es más fácil comenzar limpiando la fracción y buscando sustituir valores que eliminen$\theta$.

\[r = \dfrac{3}{1 - 2\cos(\theta)}\nonumber\]Borrar la fracción
\[r(1 - 2\cos(\theta)) = 3\nonumber\] Usar$\cos(\theta) = \dfrac{x}{r}$ para eliminar$\theta$
\[r(1 - 2\dfrac{x}{r}) = 3\nonumber\] Distribuir y simplificar
\[r - 2x = 3\nonumber\] Aislar el$r$
\[r = 3 + 2x\nonumber\] Cuadrado en ambos lados
\[r^2 = (3 + 2x)^2\nonumber\] Usar$x^2 + y^2 = r^2$
\[x^2 + y^2 = (3+2x)^2\nonumber\]

Cuando toda nuestra ecuación ha sido cargada desde$r$ y$\theta$ hacia$x$ y$y$ podemos detenernos a menos que se le pida que resuelva$y$ o simplifique.

En este ejemplo, si se desea, se podría ampliar el lado derecho de la ecuación y simplificar aún más la ecuación. Sin embargo, la ecuación no puede escribirse como una función en forma cartesiana.

Ejercicio$\PageIndex{5}$

a. Reescribir la ecuación cartesiana en forma polar:$y = \pm \sqrt{3 - x^2}$

b. Reescribir la ecuación polar en forma cartesiana:$r = 2\sin(\theta)$

Responder

a.$y = \pm \sqrt{3 - x^2}$ puede ser reescrito como$x^2 + y^2 = 3$, y se convierte$r = \sqrt{3}$

b.\[r = 2\sin(\theta)\nonumber\]
\[r= 2\dfrac{y}{r}\nonumber\]
\[r^2 = 2y\nonumber\]
\[x^2 + y^2 = 2y\nonumber\]

Ejemplo$\PageIndex{13}$

Reescribir la ecuación polar$r = \sin(2\theta)$ en forma cartesiana.

Solución

\[r = \sin(2\theta)\nonumber\]Utilice la identidad de doble ángulo para
\[r = 2\sin(\theta)\cos(\theta)\nonumber\] uso sinusoidal$\cos(\theta) = \dfrac{x}{r}$ y$\sin(\theta) = \dfrac{y}{r}$
\[r = 2 \cdot \dfrac{x}{r} \cdot \dfrac{y}{r}\nonumber\] Simplifique
\[r = \dfrac{2xy}{r^2}\nonumber\] Multiplicar por$r^2$
\[r^3 = 2xy\nonumber\] Since$x^2 + y^2 = r^2$,$r = \sqrt{x^2 + y^2}$
\[(\sqrt{x^2 + y^2})^3 = 2xy\nonumber\]

Esta ecuación también podría escribirse como

\[(x^2 + y^2)^{3/2} = 2xy\text{ or }x^2 + y^2 = (2xy)^{2/3}\nonumber\]

Temas Importantes de esta Sección

Sistema de coordenadas cartesianas
Sistema de coordenadas polares
Trazar puntos en coordenadas polares
Conversión de coordenadas entre sistemas
Ecuaciones polares: Espirales, círculos, limaçons y rosas Conversión de ecuaciones entre sistemas

\(\theta\)	0	\(\pi/4\)	\(\pi/2\)	\(3\pi/4\)	\(\pi\)	\(5\pi/4\)	\(3\pi/2\)	\(7\pi/4\)	\(2\pi\)
\(r\)	0	\(\pi/4\)	\(\pi/2\)	\(3\pi/4\)	\(\pi\)	\(5\pi/4\)	\(3\pi/2\)	\(7\pi/4\)	\(2\pi\)