8.1.1: Triángulos no rectos - Leyes de los senos y cosenos (Ejercicios)
- Page ID
- 116895
ejercicios de la sección 8.1
Resuelve los lados y ángulos desconocidos de los triángulos mostrados.
1. 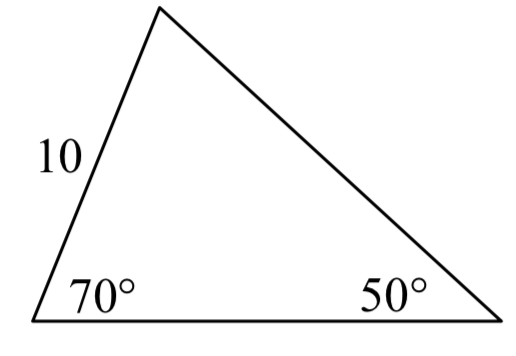 2.
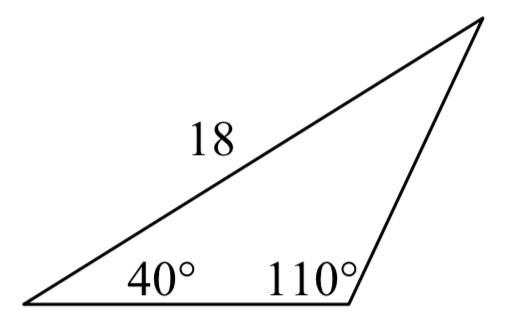
2. 
3. 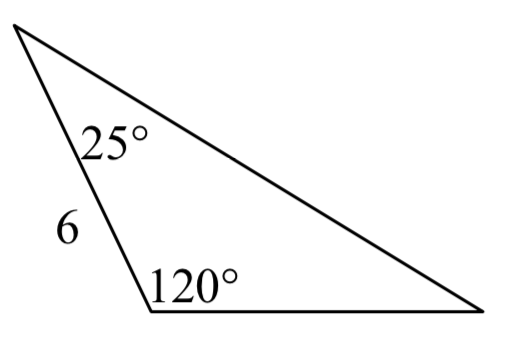 4.
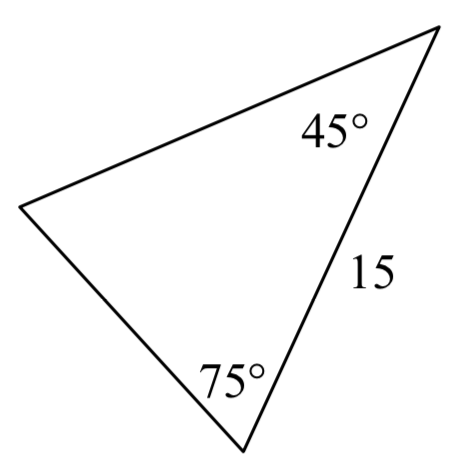
4. 
5. 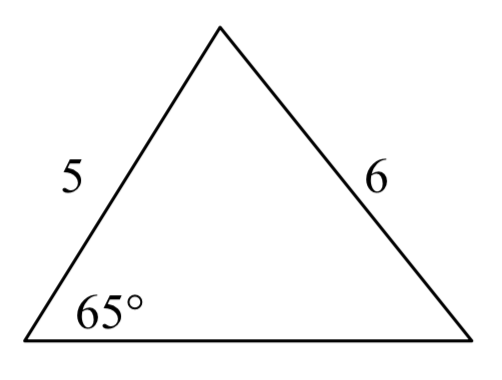 6.
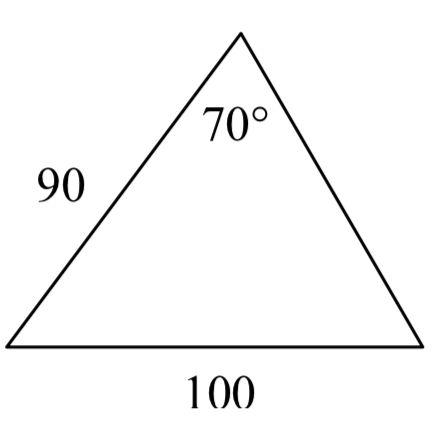
6. 
7. 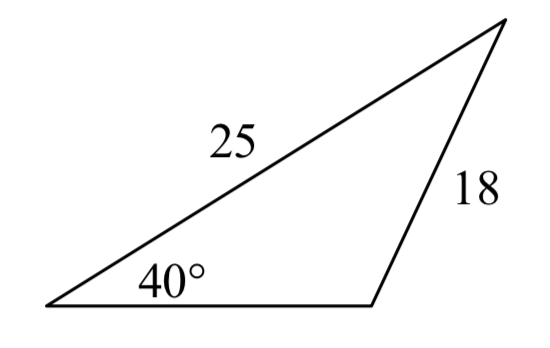 8.
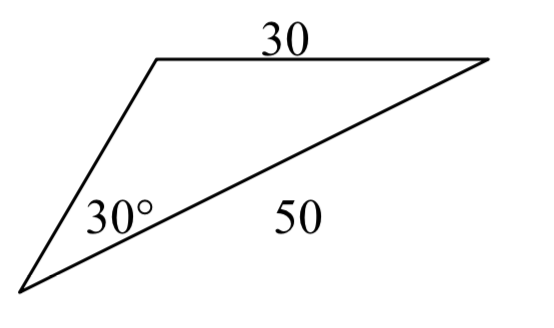
8. 
Supongamos que\(\alpha\) es lado opuesto\(a\),\(\beta\) es lado opuesto\(b\), y\(\gamma\) es lado opuesto\(c\). Resuelve cada triángulo para los lados y ángulos desconocidos si es posible. Si hay más de una solución posible, dé ambas.
9. \(\alpha = 43^{\circ}\),\(\gamma = 69^{circ}\),\(b = 20\)
10. \(\alpha = 35^{\circ}\),\(\gamma = 73^{circ}\),\(b = 19\)
11. \(\alpha = 119^{\circ}\),\(a = 26\),\(b = 14\)
12. \(\gamma = 113^{circ}\),\(b = 10\),\(c = 32\)
13. \(\beta = 50^{circ}\),\(a = 105\),\(b = 45\)
14. \(\beta = 67^{circ}\),\(a = 49\),\(b = 38\)
15. \(\alpha = 43.1^{circ}\),\(a = 184.2\),\(b = 242.8\)
16. \(\alpha = 36.6^{\circ}\),\(a = 186.2\),\(b = 242.2\)
Resuelve los lados y ángulos desconocidos de los triángulos mostrados.
17. 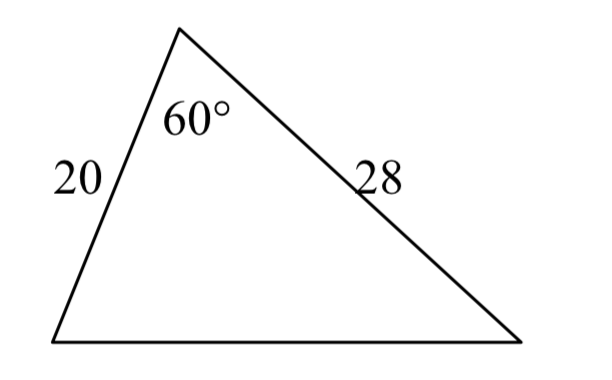 18.
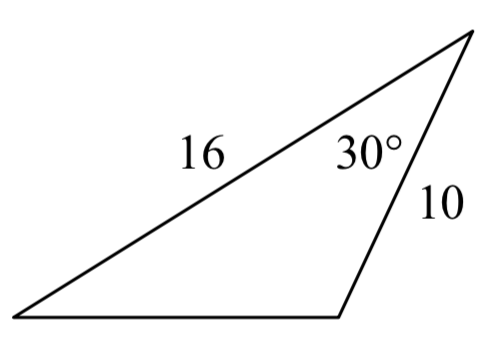
18. 
19. 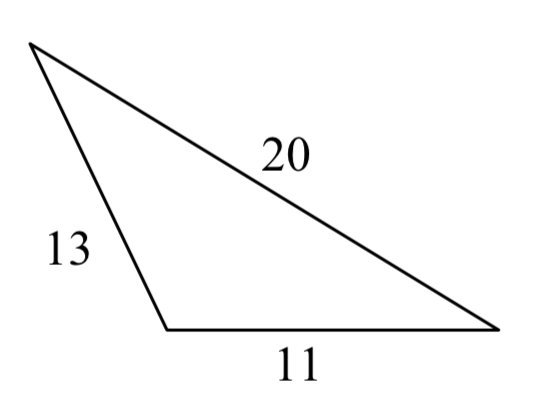 20.
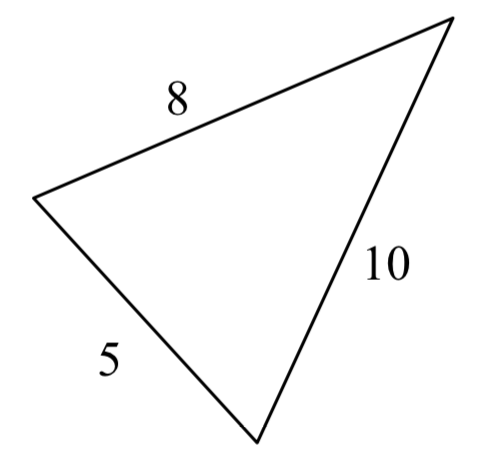
20. 
Supongamos que\(\alpha\) es lado opuesto\(a\),\(\beta\) es lado opuesto\(b\), y\(\gamma\) es lado opuesto\(c\). Resuelve cada triángulo para los lados y ángulos desconocidos si es posible. Si hay más de una solución posible, dé ambas.
21. \(\gamma = 41.2^{\circ}\),\(a = 2.49\),\(b = 3.13\)
22. \(\beta = 58.7^{\circ}\),\(a = 10.6\),\(c = 15.7\)
23. \(\alpha = 120^{\circ}\),\(b = 6\),\(c = 7\)
24. \(\gamma = 115^{\circ}\),\(a = 18\),\(b = 23\)
25. Encuentra el área de un triángulo con lados de longitud 18, 21 y 32.
26. Encuentra el área de un triángulo con lados de longitud 20, 26 y 37.
27. Para encontrar la distancia a través de un pequeño lago, un topógrafo ha tomado las medidas mostradas. Encuentra la distancia a través del lago.
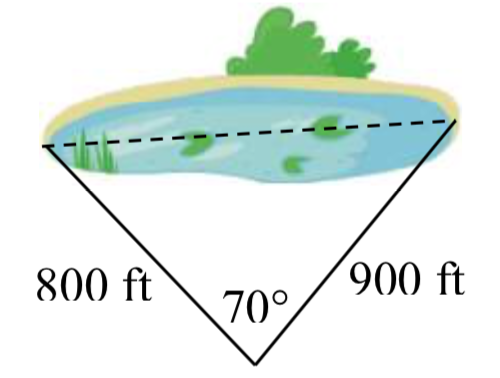
28. Para encontrar la distancia entre dos ciudades, un satélite calcula las distancias y el ángulo mostrados (\(not to scale\)). Encuentra la distancia entre las ciudades.
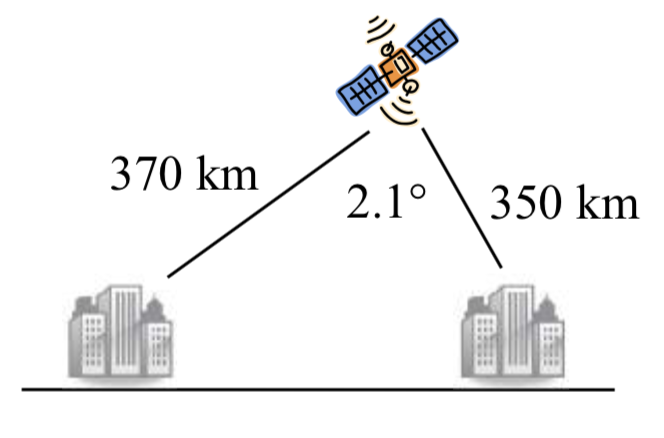
29. o determinar qué tan lejos está una embarcación de la costa, dos estaciones de radar a 500 pies de distancia determinan los ángulos hacia la embarcación, como se muestra. Encuentra la distancia del barco desde la estación A, y la distancia del barco desde la costa.
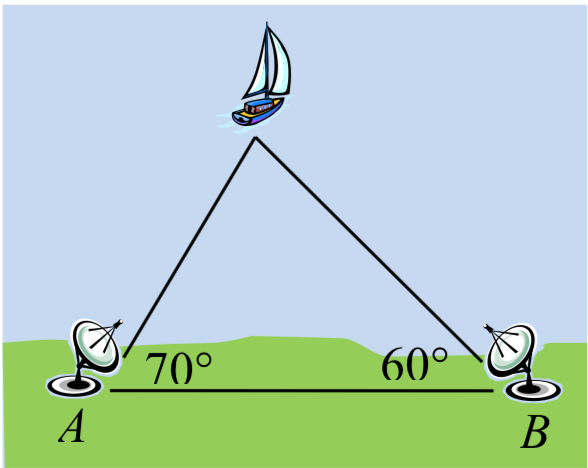
30. El camino de un satélite que orbita la tierra hace que pase directamente sobre dos estaciones de rastreo\(A\) y\(B\), que están a 69 millas de distancia. Cuando el satélite está en un lado de las dos estaciones, los ángulos de elevación en\(A\) y\(B\) se miden para ser\(86.2^{\circ}\) y\(83.9^{\circ}\), respectivamente. ¿A qué distancia está el satélite de la estación\(A\) y a qué altura está el satélite sobre el suelo?
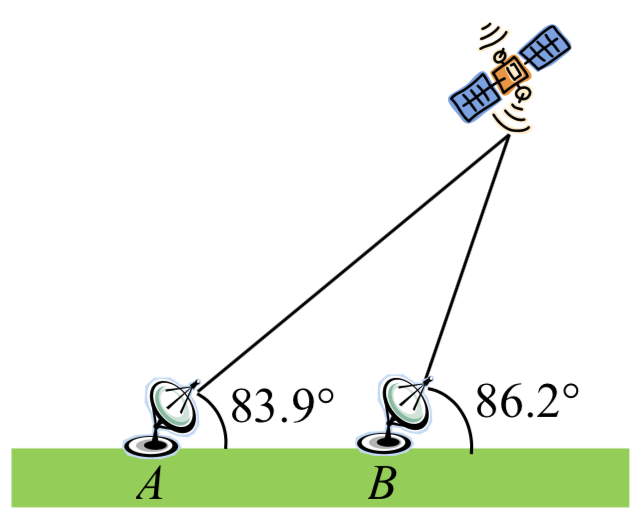
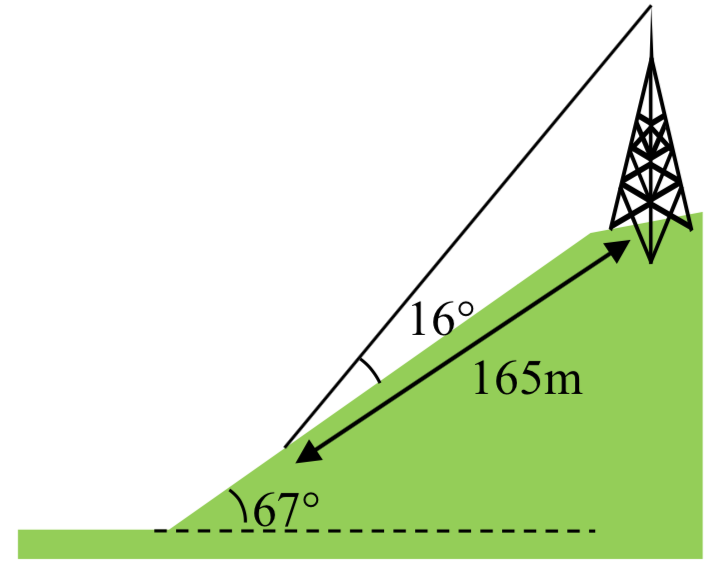
31. Una torre de comunicaciones se encuentra en lo alto de un cerro empinado, como se muestra. El ángulo de inclinación del cerro es\(67^{\circ}\). Se debe unir un cable de tipo a la parte superior de la torre y al suelo, a 165 m cuesta abajo desde la base de la torre. El ángulo formado por el chico-alambre y la colina es\(16^{\circ}\). Encuentre la longitud del cable requerida para el cable de sujeción.
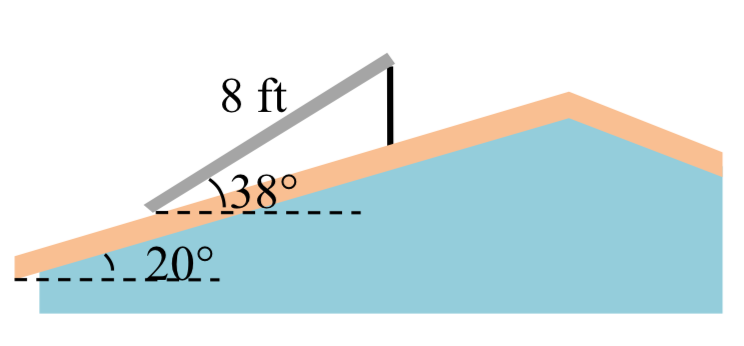
32. El techo de una casa está en\(20^{\circ}\) ángulo. Un panel solar de 8 pies debe montarse en el techo y debe estar en ángulo\(38^{\circ}\) con relación a la horizontal para obtener resultados óptimos. ¿Cuánto tiempo necesita ser el soporte vertical que sostiene la parte posterior del panel?
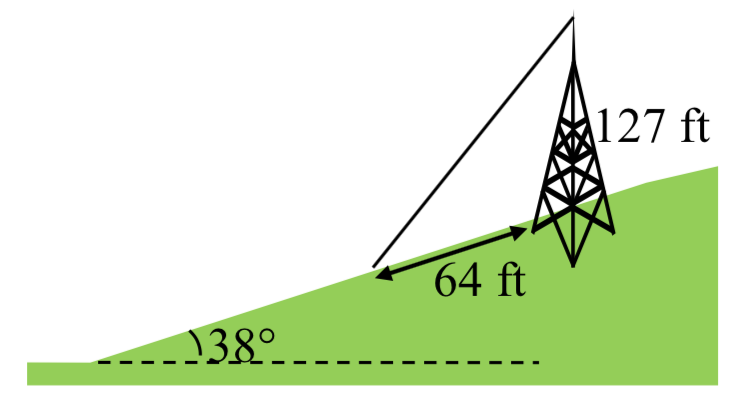
33. Una torre de 127 pies se ubica sobre un cerro que está inclinado\(38^{\circ}\) a la horizontal. Un cable de tipo se debe unir a la parte superior de la torre y anclarse en un punto a 64 pies cuesta abajo desde la base de la torre. Encuentre la longitud de cable necesaria.
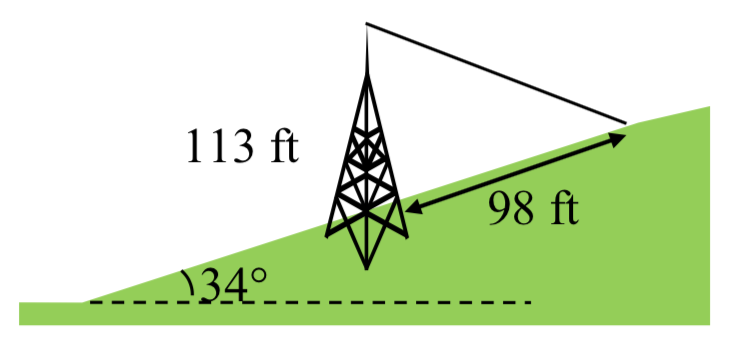
34. Una torre de 113 pies se encuentra en un cerro que está inclinado\(34^{\circ}\) a la horizontal. Un alambre tipo debe ser unido a la parte superior de la torre y anclado en un punto 98 pies cuesta arriba de la base de la torre. Encuentre la longitud de cable necesaria.
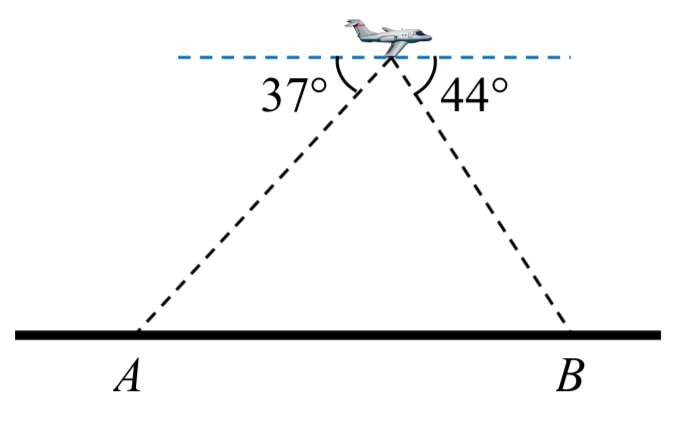
35. Un piloto sobrevuela una carretera recta. Determina los ángulos de depresión a dos postes, a 6.6 km de distancia, para ser\(37^{\circ}\) y\(44^{\circ}\), como se muestra en la figura. Encuentra la distancia del plano desde el punto\(A\), y la elevación del plano.
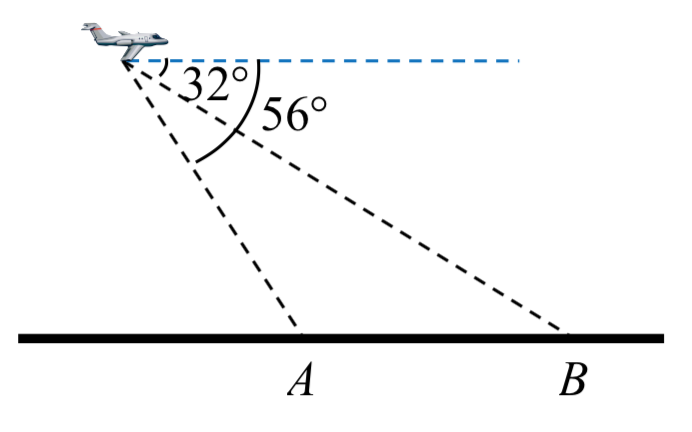
36. Un piloto sobrevuela una carretera recta. Determina los ángulos de depresión a dos postes de millas, a 4.3 km de distancia, para ser\(32^{\circ}\) y\(56^{\circ}\), como se muestra en la figura. Encuentra la distancia del plano desde el punto\(A\), y la elevación del plano.
37. Para estimar la altura de un edificio, dos estudiantes encuentran el ángulo de elevación desde un punto (a nivel del suelo) por la calle desde el edificio hasta la parte superior del edificio es\(39^{\circ}\). Desde un punto que está a 300 pies más cerca del edificio, el ángulo de elevación (a nivel del suelo) hasta la parte superior del edificio es\(50^{\circ}\). Si asumimos que la calle está nivelada, utilice esta información para estimar la altura del edificio.
38. Para estimar la altura de un edificio, dos estudiantes encuentran el ángulo de elevación desde un punto (a nivel del suelo) por la calle desde el edificio hasta la parte superior del edificio es\(35^{\circ}\). Desde un punto que está a 300 pies más cerca del edificio, el ángulo de elevación (a nivel del suelo) hasta la parte superior del edificio es\(53^{\circ}\). Si asumimos que la calle está nivelada, utilice esta información para estimar la altura del edificio.
39. Un piloto vuela en camino recto durante 1 hora 30 min. Luego hace una corrección de rumbo, encabezando 10 grados a la derecha de su curso original, y vuela 2 horas en la nueva dirección. Si mantiene una velocidad constante de 680 millas por hora, ¿a qué distancia está de su posición inicial?
40. Dos aviones salen del mismo aeropuerto al mismo tiempo. Uno vuela a 20 grados al este del norte a 500 millas por hora. El segundo vuela a 30 al este del sur a 600 millas por hora. ¿Qué tan lejos están los aviones después de 2 horas?
41. Los cuatro lados secuenciales de un cuadrilátero tienen longitudes de 4.5 cm, 7.9 cm, 9.4 cm y 12.9 cm. El ángulo entre los dos lados más pequeños es\(117^{\circ}\). ¿Cuál es el área de este cuadrilátero?
42. Los cuatro lados secuenciales de un cuadrilátero tienen longitudes de 5.7 cm, 7.2 cm, 9.4 cm y 12.8 cm. El ángulo entre los dos lados más pequeños es\(106^{\circ}\). ¿Cuál es el área de este cuadrilátero?
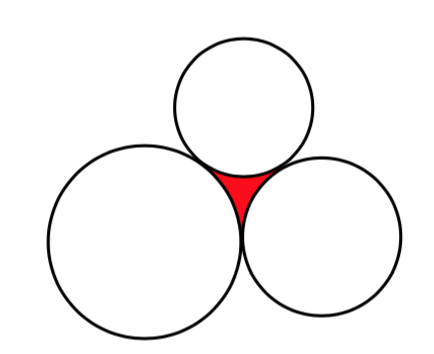
43. Tres círculos con radios 6, 7 y 8, todos tocan como se muestra. Encuentra el área sombreada delimitada por los tres círculos.
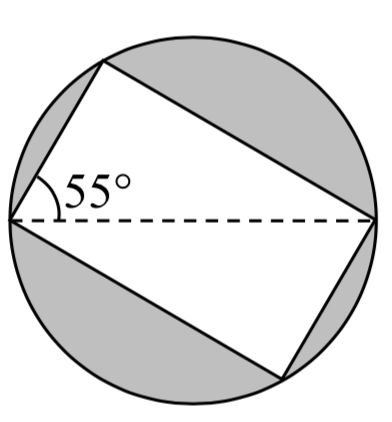
44. Un rectángulo se inscribe en un círculo de radio de 10 cm como se muestra. Encuentra el área sombreada, dentro del círculo pero fuera del rectángulo.
- Responder
-
1.
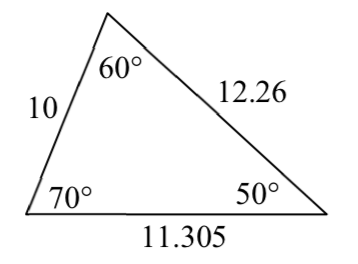
3.
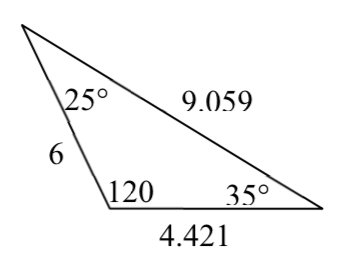
5.
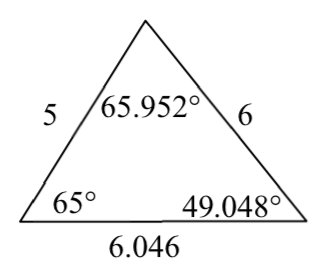
7.
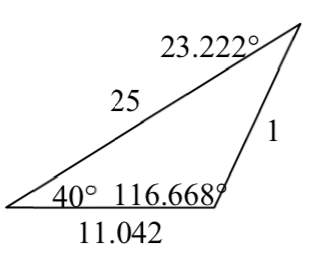
9. \(\beta = 68^(\circ)\),\(a = 14.711\),\(c = 20.138\)
11. \(\beta = 28.096^(\circ)\),\(\gamma = 32.904^(\circ)\),\(c = 16.149\)
13. No es posible.
15. \(\beta = 64.243^(\circ)\),\(\gamma = 72.657^(\circ)\),\(c = 257.328\) OR\(\beta = 115.757^(\circ)\),\(\gamma = 21.143^(\circ)\),\(c = 97.238\)
17.
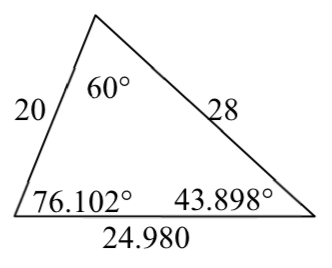
19.
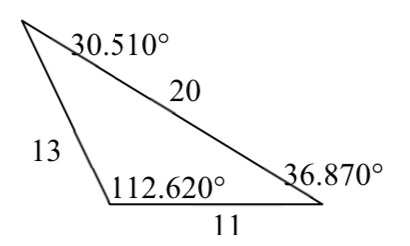
21. \(c = 2.066\),\(\alpha = 52.545^(\circ)\),\(\beta = 86.255^(\circ)\)
23. \(\alpha = 11.269\),\(\beta = 27.457^(\circ)\),\(\gamma = 32.543^(\circ)\)
25. 177.562
27. 978.515 ft
29. Distancia a A: 565.258ft. Distancia a la costa: 531.169 ft
31. 529.014
33. 173.877 pies
35. 4.642 km, 2.794 km
37. 757.963 ft
39. 2371.129 millas
41. 65.375 cm\(^(2)\)
43. 7.72


