8.4: Vectores

Última actualización
Guardar como PDF

Page ID: 116906

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Una mujer sale de casa, camina 3 millas al norte, luego 2 millas al sureste. ¿Qué tan lejos está de casa y en qué dirección tendría que caminar para regresar a casa? ¿Hasta dónde ha caminado para cuando llega a casa?

Esta pregunta puede parecer familiar —de hecho hicimos un problema similar con un barco en la primera sección de este capítulo. En esa sección, resolvimos el problema usando triángulos. En esta sección, investigaremos otra forma de abordar el problema utilizando vectores, una entidad geométrica que indica tanto una distancia como una dirección. Comenzaremos nuestra investigación utilizando una visión puramente geométrica de los vectores.

Una vista geométrica de vectores

Definición: VECTOR

Un vector es un objeto que tiene tanto una longitud como una dirección.

Geométricamente, un vector puede ser representado por una flecha que tiene una longitud fija y

indica una dirección. Si, comenzando en el punto$A$, un vector, que significa “portador” en latín, se mueve hacia el punto$B$, escribimos$\overrightarrow{AB}$ para representar el vector.

Un vector también se puede indicar usando una sola letra en negrilla, como u, o rematando la letra que representa el vector con una flecha, como$\vec{u}$.

Ejemplo$\PageIndex{1}$

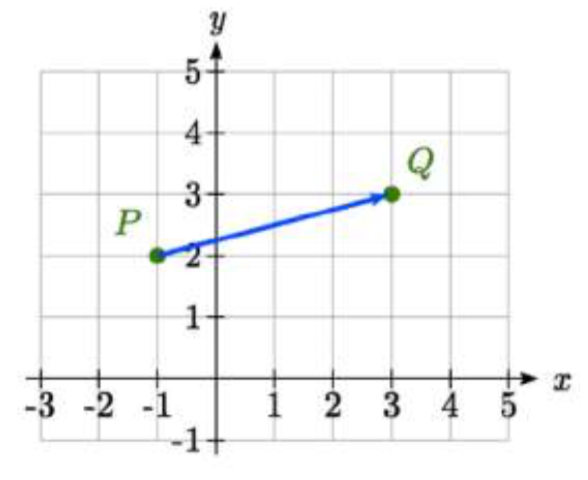
Dibuja un vector que represente el movimiento desde el punto$P$ (-1, 2) hasta el punto$Q$ (3, 3)

Solución

Dibujando una flecha desde el primer punto hasta el segundo, podemos construir un vector$\overrightarrow {PQ}$.

$Una cuadrícula de coordenadas con el punto P etiquetado en -1 coma 2 y el punto Q etiquetado en 3 coma 3, y una flecha dibujada de P a Q.$

Ejercicio$\PageIndex{1}$

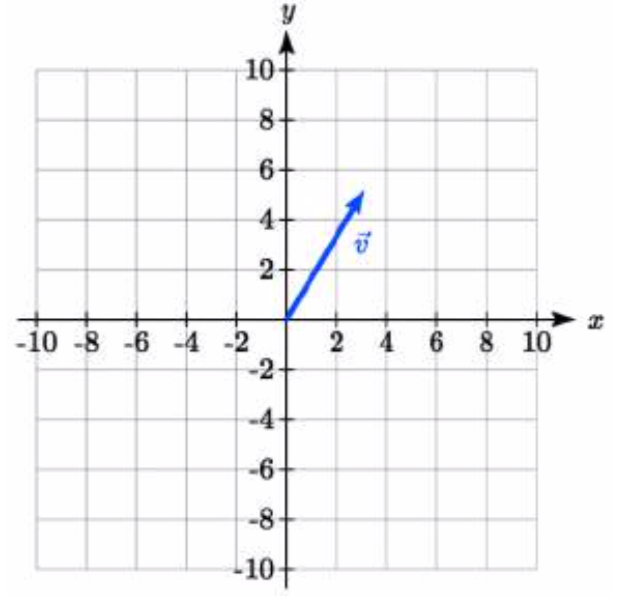
Dibuja un vector$\vec{v}$,, que viaja desde el origen hasta el punto (3, 5).

Contestar: $Un vector v dibujado desde el origen hasta 3 coma 5$

Usando esta representación geométrica de vectores, podemos visualizar la adición y escalado de vectores.

Para agregar vectores, vislumbramos una suma de dos movimientos. Para encontrar$\vec{u} + \vec{v}$, primero dibujamos el vector$\vec{u}$, luego desde el final$\vec{u}$ dibujamos el vector$\vec{v}$. Esto corresponde a la noción de que primero nos movemos a lo largo del primer vector, y luego desde esa posición final nos movemos a lo largo del segundo vector. La suma$\vec{u} + \vec{v}$ es el nuevo vector que viaja directamente desde el principio$\vec{u}$ hasta el final de$\vec{v}$ en un camino recto.

Adición de vectores geométricamente

Para agregar vectores geométricamente, dibuje$\vec{v}$ comenzando desde el final de$\vec{u}$. La suma$\vec{u} + \vec{v}$ es el vector desde el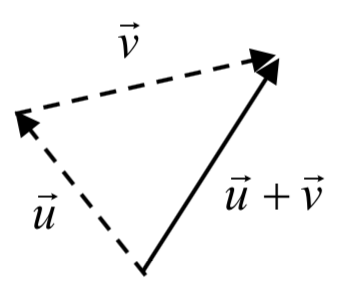 $Se dibuja un vector u discontinua. Desde el final de u se dibuja un segundo vector v discontinuo. Se dibuja un tercer vector desde el inicio de u hasta el final de v, etiquetado como u más v.$ inicio$\vec{u}$ hasta el final de$\vec{v}$.

Ejemplo$\PageIndex{2}$

Dados los dos vectores que se muestran a continuación, dibujar$\vec{u} + \vec{v}$

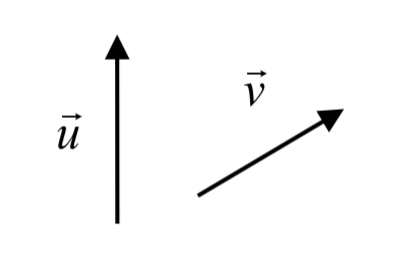
$Se dibujan dos vectores. Vector u puntos verticalmente. Vector v apunta a la parte superior derecha.$

Solución

Dibujamos$\vec{v}$ comenzando desde el final de$\vec{u}$, luego dibujamos la suma$\vec{u} + \vec{v}$ desde el principio$\vec{u}$ hasta el final de$\vec{v}$.

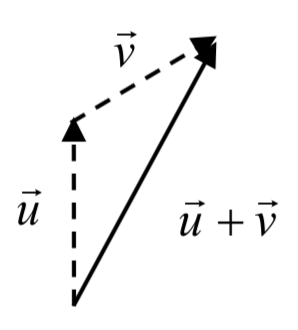
$El vector u se dibuja verticalmente. Desde el final de u vector v se dibuja hacia la parte superior derecha. Un vector desde el inicio de u hasta el final de v se dibuja etiquetado como u más v.$

Observe que el camino de la mujer caminante desde el inicio de la sección podría visualizarse como la suma de dos vectores. El vector de suma resultante indicaría su posición final relativa al inicio.

Aunque los vectores pueden existir en cualquier parte del plano, si ponemos el punto de partida en el origen es fácil entender su tamaño y dirección relativa a otros vectores.

Para escalar vectores por una constante, tal como$3\vec{u}$, podemos imaginarnos sumando$\vec{u} + \vec{u} + \vec{u}$. El resultado será un vector tres veces más largo en la misma dirección que el vector original. Si tuviéramos que escalar un vector por un número negativo, tal como$-\vec{u}$, podemos vislumbrar esto como lo contrario de$\vec{u}$; el vector para que nos$\vec{u} + (-\vec{u}$ devuelva al punto de partida. Este vector$-\vec{u}$ apuntaría en la dirección opuesta como$\vec{u}$ pero tendría la misma longitud.

Otra forma de pensar en escalar un vector es mantener su dirección y multiplicar su longitud por una constante, de modo que$3\vec{u}$ apuntaría en la misma dirección pero será 3 veces más largo.

Escalar un vector geométricamente

Para escalar geométricamente un vector por una constante, escala la longitud del vector por la constante.

El escalado de un vector por una constante negativa invertirá la dirección del vector.

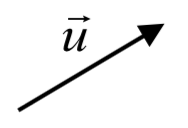
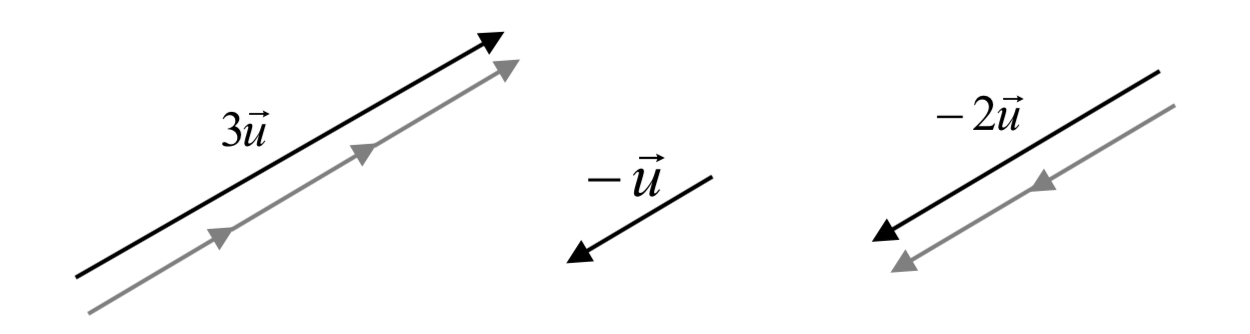
Ejemplo$\PageIndex{3}$

Dado el vector mostrado, dibujar$3\vec{u}$$-\vec{u}$, y$-2\vec{u}$.

$Un vector etiquetado u apunta a la parte superior derecha$

Solución

El vector$3\vec{u}$ será tres veces más largo. El vector$-\vec{u}$ tendrá la misma longitud pero apuntará en dirección opuesta. El vector$-2\vec{u}$ apuntará en la dirección opuesta y será el doble de largo.

$Un vector etiquetado 3u apunta a la parte superior derecha, tres veces más largo que u. Un vector etiquetado negativo u apunta a la parte inferior izquierda en la dirección opuesta a u. Un vector etiquetado negativo 2 u apunta a la parte inferior izquierda, el doble de largo que u en la dirección opuesta.$

Al combinar escalado y suma, podemos encontrar la diferencia entre vectores geométricamente también, ya que$\vec{u} - \vec{v} = \vec{u} + (-\vec{v})$.

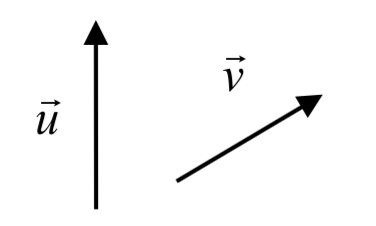
Ejemplo$\PageIndex{4}$

Dados los vectores mostrados, dibujar$\vec{u} - \vec{v}$

$Se dibujan dos vectores. Vector u puntos verticalmente. Vector v apunta a la parte superior derecha.$

Solución

Desde el final de$\vec{u}$ dibujamos$-\vec{v}$, luego dibujamos el resultado.

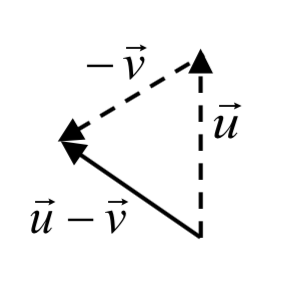
$El vector u apunta verticalmente. Desde el final de u, se dibuja el vector negativo v apuntando hacia la parte inferior izquierda. Se dibuja un vector desde el inicio de u hasta el final de v negativo, etiquetado como u menos v.$

Observe que la suma y diferencia de dos vectores son las dos diagonales de un paralelogramo con los vectores$\vec{u}$ y$\vec{v}$ como e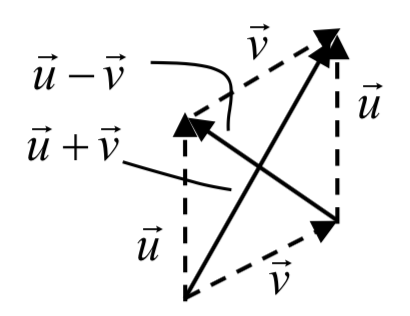 $Se muestra un paralelgramo, con los vectores u y v constituyendo los lados del paralelgramo. Las diagonales están etiquetadas con u más v y u menos v.$ dges.

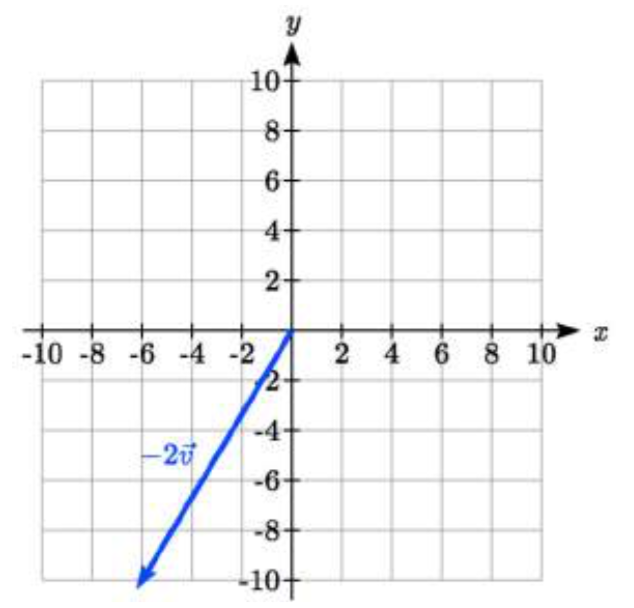
Ejercicio$\PageIndex{2}$

Usando vector$\vec{v}$ del Ejercicio anterior, dibuja$-2 \vec{v}$.

Contestar: $Un vector etiquetado negativo 2 v dibujado desde el origen a negativo 6 coma negativo 10$

Forma componente de vectores

Si bien la interpretación geométrica de los vectores nos da una comprensión intuitiva de los vectores, no nos proporciona una manera conveniente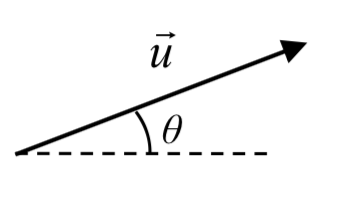 $Se muestra un vector u apuntando a la parte superior derecha. El ángulo desde la horizontal positiva en sentido contrario a las agujas del reloj hasta el vector se etiqueta theta.$ de hacer cálculos. Para ello, necesitamos una manera práctica de representar vectores. Dado que un vector implica una longitud y una dirección, sería lógico querer representar un vector usando una longitud y un ángulo$\theta$, generalmente medidos desde la posición estándar.

Definición: MAGNITUD Y DIRECCIÓN DE UN VECTOR

Un vector se$\vec{u}$ puede describir por su magnitud, o longitud$|\vec{u}|$, y un ángulo$\theta$.

Un vector con longitud 1 se llama vector unitario.

Si bien esto es muy razonable, y una forma común de describir vectores, a menudo es más conveniente que los cálculos representen un vector por componentes horizontales y verticales.

FORMA COMPONENTE DE UN VECTOR

La forma componente de un vector representa el vector usando dos componentes. $\vec{u} = \langle x, y \rangle$indica que el vector representa un desplazamiento de$x$ unidades horizontalmente y$y$ unidades verticalmente.

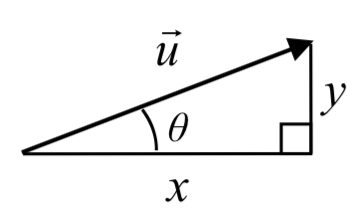
$Se muestra un triángulo a la derecha. La hipotenusa tiene una flecha y está etiquetada como vector u. La pata vertical está etiquetada con y y la pata horizontal está etiquetada con x. El ángulo desde la pata x hasta la hipotenusa se etiqueta theta.$

Observe cómo podemos ver la magnitud del vector como la longitud de la hipotenusa de un triángulo rectángulo, o en forma polar como el radio,$r$.

Notación alternativa para componentes vectoriales

En ocasiones es posible que veas vectores escritos como la combinación de vectores unitarios$\vec{i}$ y$\vec{j}$, donde$\vec{i}$ apunta la derecha y$\vec{j}$ apunta hacia arriba. En otras palabras,$\vec{i} = \langle 1, 0 \rangle$ y$\vec{j} = \langle \theta, 1 \rangle$.

En esta notación, el vector se$\vec{u} = \langle 3, -4 \rangle$ escribiría como$\vec{u} = 3\vec{i} - 4\vec{j}$ ya que ambos indican un desplazamiento de 3 unidades a la derecha, y 4 unidades hacia abajo.

Si bien puede ser conveniente pensar en el vector$\vec{u} = \langle x, y \rangle$ como una flecha desde el origen hasta el punto ($x$,$y$), asegúrese de recordar que la mayoría de los vectores pueden estar situados en cualquier parte del plano, y simplemente indican un desplazamiento (cambio de posición) en lugar de una posición.
Es común necesitar convertir de una magnitud y ángulo a la forma componente del vector y viceversa. Felizmente, este proceso es idéntico a convertir de coordenadas polares a coordenadas cartesianas, o de la forma polar de números complejos a la$a+bi$ forma.

Ejemplo$\PageIndex{5}$

Encuentra la forma componente de un vecor con longitud 7 en un ángulo de 135 grados.

Solución

Usando las fórmulas de conversión$x = r\cos(\theta)$ y$y = r\sin(\theta)$, podemos encontrar los componentes

\[x = 7 \cos (135^{\circ}) = -\dfrac{7\sqrt{2}}{2}\nonumber\]
\[y = 7 \sin (135^{\circ}) = \dfrac{7\sqrt{2}}{2}\nonumber\]

El vector se puede escribir en forma de componente como$\langle -\dfrac{7\sqrt{2}}{2}, \dfrac{7\sqrt{2}}{2} \rangle$

Ejemplo$\PageIndex{6}$

Encuentra la magnitud y el ángulo$\theta$ que representa el vector$\vec{u} = \langle 3, -2 \rangle$.

Solución

Primero podemos encontrar la magnitud recordando la relación entre$x$,$y$ y$r$:

\[r^2 = 3^2 + (-2)^2 = 13\nonumber\]
\[r = \sqrt{13}\nonumber\]

En segundo lugar podemos encontrar el ángulo. Usando la tangente,

\[\tan(\theta) = \dfrac{-2}{3}\nonumber\]
\[\theta = \tan^{-1}(-\dfrac{2}{3}) \approx -33.69^{\circ}\nonumber\]o escrito como un ángulo positivo coterminal,$326.31^{\circ}$. Este ángulo está en el$4^{\text{th}}$ cuadrante según se desee.

Ejercicio$\PageIndex{3}$

Usando vector$\vec{v}$ del primer Ejercicio, el vector que viaja desde el origen hasta el punto (3, 5), encuentra los componentes, magnitud y ángulo$\theta$ que representan este vector.

Contestar: \[\vec{v} = \langle 3, 5 \rangle \nonumber\]
\[\text{magnitude} = \sqrt{34}\nonumber\]
\[\theta = \tan^{-1} (\dfrac{5}{3}) = 59.04^{\circ}\nonumber\]

Además de representar movimientos de distancia, los vectores se utilizan comúnmente en física e ingeniería para representar cualquier cantidad que tenga tanto dirección como magnitud, incluyendo velocidades y fuerzas.

Ejemplo$\PageIndex{7}$

Un objeto es lanzado con una velocidad inicial de 200 metros por segundo en un ángulo de 30 grados. Encuentra las velocidades horizontales y verticales iniciales.

Solución

Al ver la velocidad inicial como un vector, podemos resolver el vector en componentes horizontales y verticales. 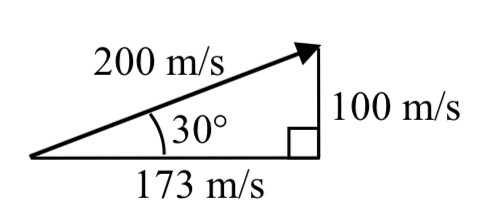$Se muestra un triángulo rectángulo. La hipotenusa es un vector, etiquetado 200 metros por segundo. La pata vertical está etiquetada con 100 metros por segundo, y la pata horizontal está etiquetada con 173 metros por segundo. El ángulo de la horizontal al vector es de 30 grados.$

\[x = 200 \cos(30^{\circ} = 200 \cdot \dfrac{\sqrt{3}}{2} \approx 173.205\text{ m/sec}\nonumber\]
\[y = 200 \sin(30^{\circ} = 200 \cdot \dfrac{1}{2} = 100\text{ m/sec}\nonumber\]

Esto nos dice que, a falta de resistencia al viento, el objeto viajará horizontalmente a unos 173 metros cada segundo. La gravedad hará que la velocidad vertical cambie con el tiempo; dejaremos una discusión sobre eso a las clases de física o cálculo.

Agregar y escalar vectores en forma de componente

Para agregar vectores en forma de componentes, simplemente podemos agregar los componentes correspondientes. Para escalar un vector por una constante, escalamos cada componente por esa constante.

Combinación de vectores en forma de componentes

Para sumar, restar o escalar vectores en forma de componente

Si$\vec{u} = \langle u_1, u_2 \rangle$,$\vec{v} = \langle v_1, v_2 \rangle$, y$c$ es alguna constante, entonces

\[\vec{u} + \vec{v} = \langle u_1 + v_1, u_2 + v_2 \rangle\]
\[\vec{u} - \vec{v} = \langle u_1 - v_1, u_2 - v_2 \rangle\]
\[c\vec{u} = \langle cu_1, cu_2 \rangle\]

Ejemplo$\PageIndex{8}$

Dado$\vec{u} = \langle 3, -2 \rangle$ y$\vec{v} = \langle -1, 4 \rangle$, encontrar un nuevo vector$\vec{w} = 3\vec{u} - 2\vec{v}$

Solución

Usando los vectores dados,

\[\begin{array} {rcl} {\vec{w}} &= & {3\vec{u} - 2\vec{v}} \\ {} &= & {3 \langle 3, -2 \rangle - 2\langle -1, 4 \rangle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{Scale each vector}} \\ {} &= & {\langle 9, -6 \rangle - \langle -2, 8 \rangle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{Subtract corresponding components}} \\ {} &= & {\langle 11, -14 \rangle} \end{array}\nonumber\]

Al representar vectores en forma de componentes, podemos encontrar el vector de desplazamiento resultante después de una multitud de movimientos sin necesidad de dibujar muchos triángulos complicados no rectos. Por un ejemplo sencillo, revisamos el problema desde la apertura de la sección. El procedimiento general que seguiremos es:

1) Convertir vectores a forma de componente
2) Agregar los componentes de los vectores
3) Convertir de nuevo a longitud y dirección si es necesario para adaptarse al contexto de la pregunta

Ejemplo$\PageIndex{9}$

Una mujer sale de casa, camina 3 millas al norte, luego 2 millas al sureste. ¿Qué tan lejos está de casa y qué dirección necesitaría caminar para regresar a casa? ¿Hasta dónde ha caminado para cuando llega a casa?

Solución

Empecemos por entender la pregunta con un poco más de profundidad. Cuando usamos vectores para describir una dirección de desplazamiento, a menudo colocamos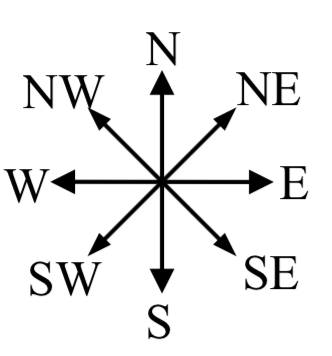 $Se muestra una imagen de las direcciones de la brújula: N apuntando hacia arriba, E apuntando a la derecha, W apuntando a la izquierda y S apuntando En el medio se encuentran direcciones como NE, apuntando hacia la parte superior derecha.$ gs delgados de manera que apunta al norte en dirección ascendente, este apunta a la derecha, y así sucesivamente, como se muestra aquí.

En consecuencia, viajar NW, SW, NE o SE, significa que estamos viajando a través del cuadrante bordeado por las direcciones dadas en un ángulo de 45 grados.

Con esto en mente, comenzamos por convertir cada vector en componentes.

Un paseo 3 millas al norte sería, en componentes,$\langle 0, 3 \rangle$.

Un paseo de 2 millas al sureste estaría en un ángulo del$45^{\circ}$ Sur del Este. Midiendo desde la posición estándar el ángulo sería$315^{\circ}$.

Al convertir a componentes, elegimos usar el ángulo de posición estándar para que no tengamos que preocuparnos por si los signos son negativos o positivos; funcionarán automáticamente.

\[\langle 2\cos (315^{\circ}),\: 2\sin (315^{\circ })\rangle = \langle 2\cdot\frac{\sqrt{2}}{2},\:2\cdot\frac{-\sqrt{2}}{2}\rangle\approx\langle 1.414, -1.414\rangle\nonumber\]

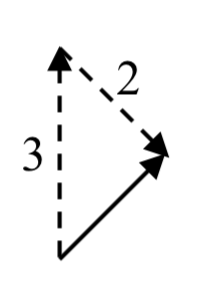
$Se muestra un vector apuntando hacia arriba con longitud 3. Desde el final de la misma, hay un vector de longitud 2 apuntando a la parte inferior derecha. Desde el inicio de la primera hasta el final del segundo se dibuja el vector suma.$

Agregar estos vectores da la suma de los movimientos en forma de componente

\[\langle 0, 3 \rangle + \langle 1.414, -1.414 \rangle = \langle 1.414 1.586 \rangle\nonumber\]

Para saber qué tan lejos está de casa y la dirección que necesitaría caminar para regresar a casa, podríamos encontrar la magnitud y el ángulo de este vector.

\[\text{Length} = \sqrt{1.414^2 + 1.586^2} = 2.125\nonumber\]

Para encontrar el ángulo, podemos usar la tangente

\[\tan(\theta) = \dfrac{1.586}{1.414}\nonumber\]
\[\theta = tan^{-1} (\dfrac{1.586}{1.414}) = 48.273^{\circ}\text{ north of east}\nonumber\]

Por supuesto, este es el ángulo desde su punto de partida hasta su punto final. Para regresar a casa, necesitaría dirigirse en dirección opuesta, que podríamos describir como$180^{\circ} + 48.273^{\circ} = 228.273^{\circ}$ medida en posición estándar, o como$48.273^{\circ}$ sur de oeste (u$41.727^{\circ}$ oeste de sur).

Ella ha caminado una distancia total de 3 + 2 + 2.125 = 7.125 millas.

Tenga en cuenta que la distancia total recorrida no es la misma que la longitud del vector de desplazamiento resultante o el vector de “retorno”.

Ejercicio$\PageIndex{4}$

En una búsqueda del tesoro, se dan indicaciones para encontrar un tesoro enterrado. Desde un punto de partida en un asta de bandera debes caminar 30 pies hacia el este, girar 30 grados hacia el norte y recorrer 50 pies, para luego girar hacia el sur y recorrer 75 pies. Dibuja una imagen de estos vectores, encuentra sus componentes y calcula qué tan lejos y en qué dirección debes viajar para ir directamente al tesoro desde el asta de la bandera sin seguir el mapa.

Contestar

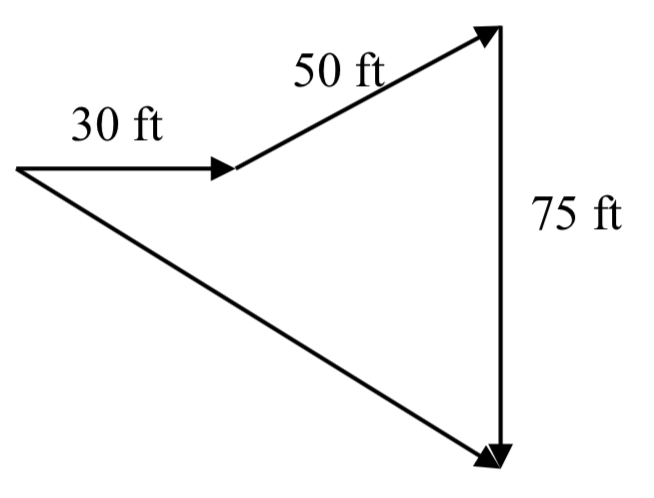
$Un vector de longitud 30 pies apuntando a la derecha. Desde el final de la misma, un vector de 50 pies apuntando a la parte superior derecha. Desde el final de la misma, un vector de 75 pies apuntando hacia abajo. Se dibuja un vector de suma desde el inicio del primero hasta el final de los últimos vectores.$

\[\vec{v}_1 = \langle 30, 0 \rangle\quad \vec{v}_2 = \langle 50\cos(30^{\circ}), 50\sin(30^{circ}) \rangle\quad \vec{v}_3 = \langle 0, -75 \rangle\nonumber\]
\[\vec{v}_f = \langle 30 + 50 \cos(30^{\circ}), 50 \sin(30^{\circ}) - 75 \rangle = \langle 73.301, -50 \rangle\nonumber\]
Magnitud = 88.73 pies en ángulo$34.3^{\circ}$ al sur del este.

Si bien usar vectores no es mucho más rápido que usar la ley de los cosenos con solo dos movimientos, al combinar tres o más movimientos, fuerzas u otras cantidades de vectores, usar vectores rápidamente se vuelve mucho más eficiente que tratar de usar triángulos.

Ejemplo$\PageIndex{10}$

Tres fuerzas están actuando sobre un objeto como se muestra a continuación, cada una medida en Newtons (N). ¿Qué fuerza se debe ejercer para mantener el objeto en equilibrio (donde la suma de las fuerzas es cero)?

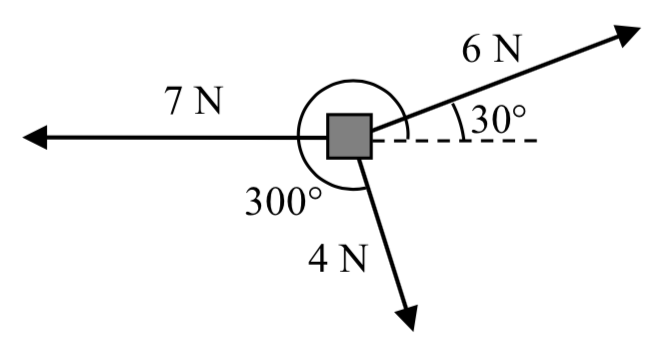
$Se muestra un objeto en el centro, con tres vectores de fuerza que salen de él: Un vector de 6 Newton apuntando 30 grados en sentido antihorario desde la horizontal positiva, un vector de 7 Newton apuntando a la izquierda y un vector de 4 Newton apuntando 300 grados en sentido antihorario desde la horizontal positiva.$

Solución

Comenzamos resolviendo cada vector en componentes.

El primer vector con magnitud 6 Newtons en un ángulo de 30 grados tendrá componentes

\[\langle 6\cos(30^{\circ}). 6\sin(30^{\circ}) \rangle = \langle 6 \cdot \dfrac{\sqrt{3}}{2}, 6 \cdot \dfrac{1}{2} \rangle = \langle 3\sqrt{3} 3 \rangle\nonumber\]

El segundo vector es sólo en la dirección horizontal, por lo que se puede escribir como$\langle -7, 0 \rangle$.

El tercer vector con magnitud 4 Newtons en un ángulo de 300 grados tendrá componentes

\[\langle 4 \cos(300^{\circ}), 4\sin(300^{\circ}) \rangle = \langle 4 \cdot \dfrac{1}{2}, 4 \cdot \dfrac{-\sqrt{3}}{2} \rangle = \langle 2, -2\sqrt{3} \rangle\nonumber\]

Para mantener el objeto en equilibrio, necesitamos encontrar un vector de fuerza$x$,$y$ por lo que la suma de los cuatro vectores es el vector cero,$\langle 0, 0 \rangle$.

\[\langle 3\sqrt{3}, 3 \rangle + \langle -7, 0 \rangle + \langle 2, -2\sqrt{3} \rangle + \langle x, y \rangle = \langle 0, 0 \rangle\nonumber\]Agregar componentes
\[\langle 3\sqrt{3} - 7 + 2, 3 + 0 - 2\sqrt{3} \rangle + \langle x, y \rangle = \langle 0, 0 \rangle\nonumber\] Simplify
\[\langle 3\sqrt{3} - 5, 3 - 2\sqrt{3} \rangle + \langle x, y \rangle = \langle 0, 0 \rangle\nonumber\] Solve
\[\langle x, y \rangle = \langle 0, 0 \rangle - \langle 3\sqrt{3} - 5, 3 - 2\sqrt{3} \rangle\nonumber\]
\[\langle x, y \rangle = \langle -3\sqrt{3} + 5, -3 + 2\sqrt{3} \rangle \approx \langle -0.196, 0.464 \rangle\nonumber\]

Este vector da en componentes la fuerza que habría que aplicar para mantener el objeto en equilibrio. Si se desea, podríamos encontrar la magnitud de esta fuerza y dirección en la que habría que aplicar.

\[\text{Magnitude} = \sqrt{(-0.196)^2 + 0.464^2} = 0.504\text{ N}\nonumber\]

Ángulo:

\[\tan(\theta) = \dfrac{0.464}{-0.196}\nonumber\]
\[\theta = \tan^{-1} (\dfrac{0.464}{-0.196} = -67.089^{\circ}\nonumber\]

Esto está en el cuadrante equivocado, por lo que ajustamos encontrando el siguiente ángulo con el mismo valor de tangente agregando un periodo completo de tangente:

\[\theta = -67.089^{\circ} + 180^{\circ} = 112. 911^{circ}\nonumber\]

Para mantener el objeto en equilibrio, se necesitaría aplicar una fuerza de 0.504 Newtons en un ángulo de$112.911^{\circ}$

Temas Importantes de esta Sección

Vectores, magnitud (longitud) y dirección Adición de vectores
Escalado de vectores
Componentes de vectores
Vectores como velocidad
Vectores como fuerzas
Agregar y escalar vectores en forma de componente Distancia total recorrida frente a desplazamiento total