2.1: Funciones trigonométricas de ángulos no agudos

Última actualización
Guardar como PDF

Page ID: 117029

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

2.1 Funciones trigonométricas de los ángulos no agudos
En el capítulo$1,$ aprendimos sobre las funciones trigonométricas de los ángulos agudos positivos que ocurren dentro de los triángulos rectos. Si queremos extender la definición de las funciones trigonométricas, entonces necesitamos definir cómo determinar los valores para el seno y el coseno de otros ángulos. Para ello, considere un triángulo rectángulo dibujado en los ejes de coordenadas. El ángulo agudo positivo$\theta$ será el ángulo creado entre el$x$ eje -eje y la hipotenusa del triángulo. Las longitudes de las dos patas del triángulo serán las$y$ coordenadas$x$ y de un punto en el primer cuadrante.
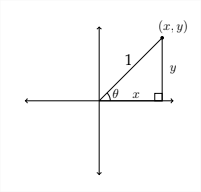
$clipboard_e31c267b0cd6633f99e8553b725ec74f2.png$

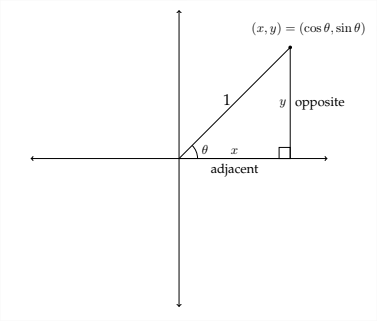
$clipboard_e0d60d9059d7786e85a627372bc090510.png$

En la imagen de arriba vemos un triángulo en el primer cuadrante con una hipotenusa de
1. En esta situación,$\sin \theta=\frac{\rho p p}{h y p}=\frac{y}{1}=y,$ cuyo valor es solo la$y$ coordenada -del punto en la parte superior del triángulo. Correspondientemente, el valor de$\cos \theta=\frac{a d j}{h y p}=$$\frac{x}{1}=x,$ o el valor$x$ de la coordenada del mismo punto.

Esto nos permite encontrar el seno o coseno para lo que se conoce como los ángulos cuadránticos - los ángulos que son múltiplos de$90^{\circ} .$ Si miramos el círculo unitario (el círculo con un radio de 1), entonces podemos ver los valores del seno y coseno para estos ángulos.

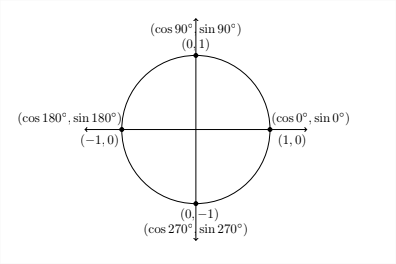
$clipboard_e51775e6d82d295f9257f54f13b8de9d1.png$

En el diagrama anterior, vemos los valores para el seno y el coseno de los ángulos cuadrangulares:
\ [ \ cos 0^ {\ circ} =1\ quad\ cos 90^ {\ circ} =0\ quad\ cos 180^ {\ circ} =-1\ quad\ cos 270^ {\ circ} =0
\] $\sin 0^{\circ}=0 \quad \sin 90^{\circ}=1 \quad \sin 180^{\circ}=0 \quad \sin 270^{\circ}=-1$
Si tomamos un radio de longitud 1 y lo giramos contra- en sentido horario en el plano de$y$ coordenadas, las coordenadas$x$ y del punto en la punta corresponderán a los valores del coseno y seno del ángulo que se crea en la rotación. Veamos un ejemplo en el segundo cuadrante. Si giramos un segmento de línea de longitud 1 por 120”, terminará en el Cuadrante II.
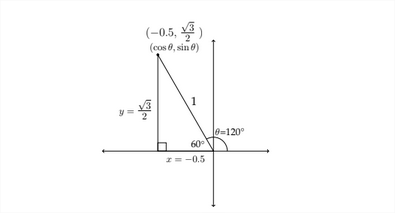
$clipboard_e3a1e889097ae0a19d1ee00ca837c27bb.png$
En el diagrama anterior notamos varias cosas. El radio de longitud 1 ha sido girado por el$120^{\text {ento }}$ Cuadrante II. Si luego dejamos caer una línea perpendicular desde el punto final del radio hasta el$x$ eje -eje, creamos un triángulo en el Cuadrante II. Observe que el ángulo suplementario a$120^{\circ}$ aparece en el triángulo y esto nos permite encontrar las longitudes de los lados del triángulo y de ahí los valores para las$y$ coordenadas$x$ y del punto en la punta del radio.

Siempre que$90^{\circ}$ se cree un ángulo mayor que en los ejes de coordenadas, simplemente suelte una perpendicular al$x$ eje. El ángulo creado es el ángulo de referencia. Los valores de las funciones trigonométricas del ángulo de rotación y el ángulo de referencia sólo diferirán en su signo$(+,-) .$ En la siguiente página hay ejemplos para Cuadrantes$\mathbb{1}$,
III y IV.

$clipboard_e64b03e3d4642a799307136eaa920a426.png$

$clipboard_e963abb1fb1c273cd235acf8136662014.png$

$clipboard_e653285009f7165d2cbb241cafcc9caaf.png$

El proceso para encontrar ángulos de referencia depende de en qué cuadrante termina el ángulo.
Ejemplos
Encuentra el ángulo de referencia para los siguientes ángulos:
$1.128^{\circ}$
$2.41^{\circ}$
$3.327^{\circ}$
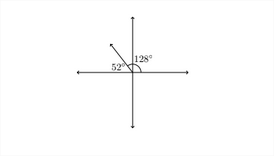
1. Un ángulo de$128^{\circ}$ termina en el Cuadrante II. Para encontrar el ángulo de referencia, restaríamos el ángulo de$180^{\circ}: \quad 180^{\circ}-128^{\circ}=52^{\circ}$

$clipboard_e937cf910af7cd6c22699c362c546b730.png$

2. Un ángulo de$241^{\circ}$ termina en el Cuadrante III. Para encontrar el ángulo de referencia, restaríamos$180^{\circ}$ del ángulo:$\quad 241^{\circ}-180^{\circ}=61^{\circ}$
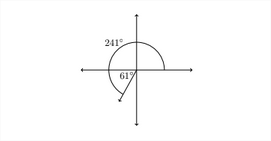
$clipboard_e073aff23423362f76511ecf5d0559489.png$
3. Un ángulo de$327^{\circ}$ termina en el Cuadrante IV. Para encontrar el ángulo de referencia, restamos el ángulo de$360^{\circ}: \quad 360^{\circ}-327^{\circ}=33^{\circ}$
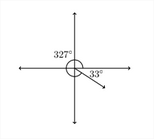
$clipboard_e05098219a4b165740b59a1f7daebcb58.png$
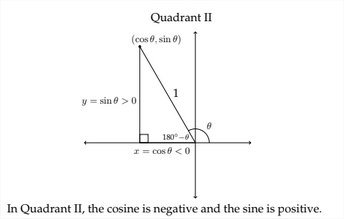
Una vez que conocemos el ángulo de referencia, podemos encontrar las funciones trigonométricas para el propio ángulo original. En ejemplo$1,$ tuvimos$128^{\circ},$ un ángulo en el Cuadrante II con un ángulo de referencia de$52^{\circ} .$ Por lo tanto, si queremos encontrar el seno, coseno y tangente de$128^{\circ},$ entonces debemos encontrar el seno, coseno y tangente de$52^{\circ}$ y aplicar el signo positivo o negativo apropiado.

Ejemplo 1 Cuadrante II
En el Cuadrante II, las$x$ coordenadas son$y$ negativas y las coordenadas son positivas. Esto significa que$\cos \theta<0$ y$\sin \theta>0 .$ Los valores para este proceso se dan a continuación:
$\sin 52^{\circ} \approx 0.7880$
$\sin 128^{\circ} \approx 0.7880$
$\cos 52^{\circ} \approx 0.6157 \quad \cos 128^{\circ} \approx-0.6157$
$\tan 52^{\circ} \approx 1.280 \quad \tan 128^{\circ} \approx-1.280^{\circ}$
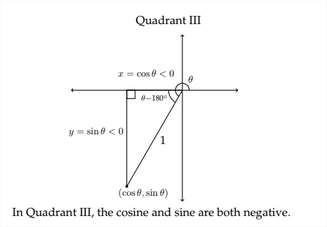
Ejemplo 2 Cuadrante III
En el Cuadrante III,$x$ -coordenadas son negativas y$y$ -coordenadas también son negativas. Esto significa que$\cos \theta<0$ y$\sin \theta<0 .$ Los valores para este proceso se dan a continuación:
$\sin 61^{\circ} \approx 0.8746 \quad \sin 241^{\circ} \approx-0.8746$
$\cos 61^{\circ} \approx 0.4848$
$\cos 241^{\circ} \approx-0.4848$
$\tan 61^{\circ} \approx 1.8040 \quad \tan 241^{\circ} \approx 1.8040$
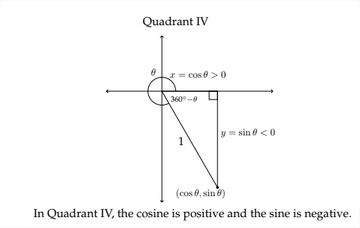
Ejemplo 3 Cuadrante IV
En el cuadrante IV,$x$ -coordenadas son las$y$ coordenadas positivas y -son negativas. Esto significa que$\cos \theta>0$ y$\sin \theta<0 .$ Los valores para este proceso se dan a continuación:
$\sin 33^{\circ} \approx 0.5446$
$\sin 327^{\circ} \approx-0.5446$
$\cos 33^{\circ} \approx 0.8387$
$\cos 327^{\circ} \approx 0.8387$
$\tan 33^{\circ} \approx 0.6494 \quad \tan 327^{\circ} \approx-0.6494$

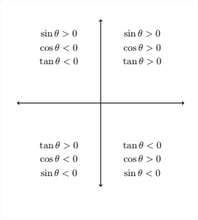
$clipboard_e5dc5691f7e27a0bd4490d5ba56859b39.png$

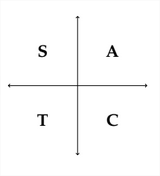
En el Cuadrante I, TODAS las funciones trigonométricas son positivas. En el Cuadrante II, la función SIN es positiva (así como la CSC).
En el Cuadrante III, la función TAN es positiva (así como la COT).
En el Cuadrante IV, la función COS es positiva (así como la SEC).
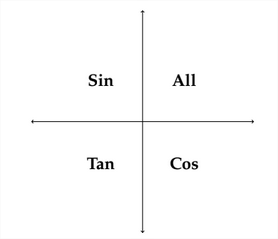
$clipboard_ee7dbd49153c83821fc497725cbdb9b37.png$
Un dispositivo monumónico común para recordar estas relaciones es la frase:
“Todos los estudiantes toman cálculo”. Esto puede ayudarte a recordar qué funciones trigonométricas son positivas en cada uno de los cuatro cuadrantes.
$clipboard_e15b4edf9ed16f50e041c87990c22cf96.png$

Ángulos de referencia para ángulos negativos Los ángulos medidos
negativamente giran en sentido horario.
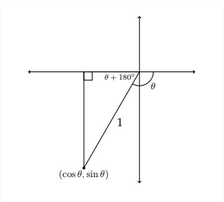
$clipboard_e485f67fb5ea133e6be1b57d9466636c1.png$
Hay una variedad de métodos para encontrar el ángulo de referencia para un ángulo de valor negativo. Se puede encontrar un ángulo positivo que es co-terminal con el ángulo negativo y luego encontrar el ángulo de referencia para el ángulo positivo. También puede soltar una perpendicular al$x$ eje -para encontrar el ángulo de referencia para el ángulo negativo directamente.

Por ejemplo, el ángulo$-120^{\circ}$ termina en el Cuadrante III y es co-terminal con el ángulo positivo$240^{\circ}$. De cualquier manera, cuando se cae una perpendicular al$x$ eje, se encuentra que el ángulo de referencia es$60^{\circ} .$

Si se le da el valor de una de las funciones trigonométricas de un ángulo$\theta$ y sabe en qué cuadrante$\theta$ se encuentra, puede encontrar las otras funciones trigonométricas para ese ángulo.
Ejemplo
Dado$\theta$ en Cuadrante$\mathrm{IV}$ con$\cos \theta=\frac{1}{5},$ hallazgo$\sin \theta$ y$\tan \theta$
Si$\cos \theta=\frac{1}{5},$ entonces el lado adyacente y la hipotenusa deben estar en una proporción de$15 .$

Podemos etiquetar estos lados como 1 y 5 y luego encontrar la longitud del tercer lado en el triángulo. Esto nos permitirá encontrar$\sin \theta$ y$\tan \theta$
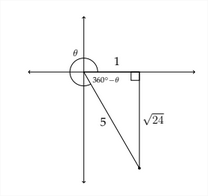
$clipboard_e38bbc5d5d3c3ae46eb646a15d63ce410.png$
Usando el Teorema de Pitágoras:
13
$25-10$
$x=1$
encontramos que el lado opuesto al ángulo de referencia para$\theta$ es$\sqrt{24}$ o $2 \sqrt{6}$. Ahora podemos encontrar$\sin \theta$ y broncearse$\theta:$
\ [ \ sin\ theta=\ frac {\ sqrt {24}} {5}
\] y
\ [ \ tan\ theta=\ frac {\ sqrt {24}} {1} =\ sqrt {24}
\]

En los problemas de esta sección se utilizan las funciones recíprocas secante, cosecante y cotangente. Recuerda que:
\ [ \ sec\ theta=\ frac {1} {\ cos\ theta} =\ frac {h y p} {a d y}
\] $\csc \theta=\frac{1}{\sin \theta}=\frac{h y p}{\alpha p p}$
$\cot \theta=\frac{1}{\tan \theta}=\frac{a d j}{o p p}$
Ejercicios 2.1
Determinar el cuadrante en el que$\theta$ se encuentra el ángulo.
1. $\cos \theta>0, \tan \theta>0$
$\sin \theta<0, \cos \theta>0$
3. $\quad \sec \theta>0, \tan \theta<0$
4. $\quad \cot \theta>0, \cos \theta<0$
5. $\sin \theta>0, \cos \theta<0$
6. $\sin \theta>0, \cot \theta>0$
7. $\sin \theta<0, \cos \theta<0$
8. $\csc \theta>0, \cot \theta<0$
Determine en qué cuadrante termina el ángulo dado y encuentre el ángulo de referencia para cada uno.
$9.195^{\circ}$
$10.330^{\circ}$
$11.120^{\circ}$
$12.210^{\circ}$
$13.135^{\circ}$
$14.300^{\circ}$
$15 . \quad-100^{\circ}$
$16.225^{\circ}$
$17 . \quad 315^{\circ}$
$18 . \frac{5 \pi}{4}$
19. $\quad-\frac{2 \pi}{3}$
$20 . \quad \frac{7 \pi}{3}$
$21 . \quad \frac{11 \pi}{4}$
$22 . \quad \frac{7 \pi}{6}$
23. $\frac{11 \pi}{6}$

Encuentra$\sin \theta, \cos \theta$ y broncea$\theta$ en cada problema.
24. $\quad \sin \theta=-\frac{12}{13}, \theta$en el Cuadrante IV
25. $\quad \cos \theta=-\frac{4}{5}, \theta$en el Cuadrante II
26. $\quad \cos \theta=\frac{1}{4}, \theta$en el Cuadrante I
27. $\quad \tan \theta=\frac{3}{2}, \theta$en el Cuadrante III
28. $\quad \tan \theta=-\frac{4}{5}, \theta$en el Cuadrante II
29. $\quad \sin \theta=\frac{3}{8}, \theta$en el Cuadrante II
30. $\quad \sin \theta=-\frac{1}{3}, \theta$en el Cuadrante III
31. $\quad \tan \theta=5, \theta$en el Cuadrante$I$
32. $\quad \sec \theta=-2, \tan \theta<0$
33. $\quad \cot \theta=\sqrt{3}, \cos \theta<0$
34. $\quad \tan \theta=-\frac{1}{3}, \sin \theta<0$
35. $\quad \csc \theta=\sqrt{2}, \cos \theta>0$
36. $\quad \cos \theta=-\frac{2}{5}, \tan \theta>0$
37. $\quad \sec \theta=2, \sin \theta<0$
38. $\quad \sin \theta=\frac{1}{\sqrt{2}}, \cos \theta>0$
39. $\quad \sin \theta=-\frac{2}{3}, \cot \theta>0$