2.2: Graficar funciones trigonométricas

Última actualización
Guardar como PDF

Page ID: 117036

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Hemos visto cómo determinar los valores de las funciones trigonométricas para los ángulos que terminan en los Cuadrantes II, III y IV. Esto nos permite hacer una gráfica de los valores de la función sinusoidal para cualquier ángulo. En la tabla a continuación, he enumerado los valores para la función sinusoidal para los ángulos entre$0^{\circ}$ y$360^{\circ} .$

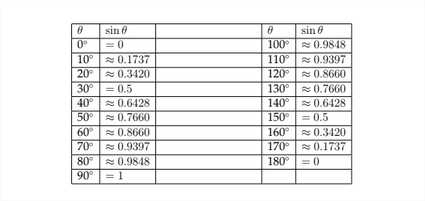
$clipboard_ecbaa7c060e98136ab9ef4c8da796cc04.png$

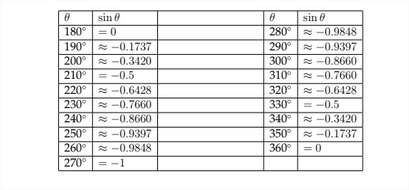
$clipboard_e7c485645d8405d9d3df38738686903fd.png$

A continuación vemos una gráfica de estos puntos trazados en los ejes de coordenadas.

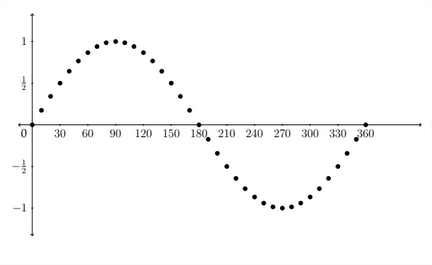
$clipboard_e00bd79757e5ffb83695fbd35b1600d87.png$

Al graficar funciones trigonométricas, normalmente usamos medidas de radianes a lo largo del$x$ eje, por lo que la gráfica generalmente se vería así:

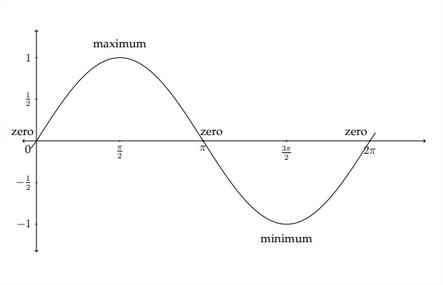
$clipboard_e36027f6d35ebd83c380f794da68a9da5.png$

El gráfico de la función sinusoidal estándar comienza en el punto cero, luego se eleva al valor máximo de 1 entre 0 y$\frac{7}{3}$ radianes. Luego vuelve a disminuir a 0 en
\ pi radianes antes de cruzar a los valores negativos y golpear su valor mínimo en$\frac{3 \pi}{2}$ radianes. Luego vuelve a subir a 0 en$2 \pi$ radianes antes de comenzar de nuevo.
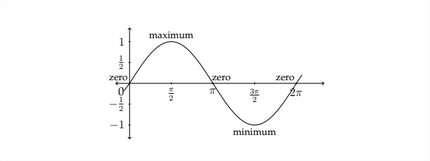
$clipboard_ef0282727bb1ab930c524eef2f2c39a11.png$
El gráfico coseno estándar se comporta de manera similar pero ligeramente diferente. Vimos antes que$\cos 0^{\circ}=1,$ así la gráfica coseno comenzaría en el punto$(0,1),$ luego disminuiría gradualmente a cero. Una imagen de la gráfica de coseno estándar se vería como la siguiente figura:
máximo
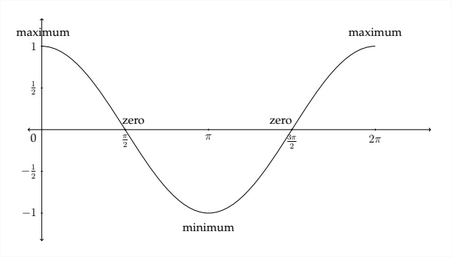
$clipboard_e77f435a00d220919700a979f860bcbf3.png$

Los gráficos de seno y coseno a veces se denominan “onda sinusoidal” o “sinusoide” y pueden ser muy útiles para modelar fenómenos que ocurren en ondas. Ejemplos de ello son el ascenso y la caída de las mareas; las ondas sonoras y la música; la electricidad; y la duración del día a lo largo del año. Las gráficas estándar de seno y coseno deben ser modificadas para que se ajusten a una aplicación particular de manera que modelarán efectivamente la situación. Las ideas que examinemos a continuación explicarán cómo modificar los gráficos de seno y coseno para adaptarse a una variedad de situaciones diferentes.

Hay cuatro aspectos a las funciones seno y coseno a tener en cuenta a la hora de hacer una gráfica. Estos son:
1) La Amplitud de la gráfica
2) El Periodo de la gráfica
3) El Desplazamiento Vertical de la gráfica
4) El Desplazamiento de Fase de la Gráfica
Amplitud
La amplitud de una función sinusoidal o coseno se refiere al máximo y al mínimo valores de la función. En las gráficas estándar de seno y coseno, el valor máximo es 1 y el valor mínimo es$-1 .$ La amplitud es la mitad de la diferencia entre los valores máximo y mínimo. En las gráficas estándar la diferencia entre el máximo y el mínimo es la$1-(-1)=2 ;$ mitad de esto es 1 por lo que la amplitud de las funciones estándar seno y coseno es$1 .$

El valor de la amplitud es también el valor absoluto del coeficiente de la expresión sinusoidal o coseno. En la gráfica estándar,$y=\sin x,$ el coeficiente de la función sinusoidal es$1,$ así que la amplitud es$1 .$ En la función$y=2 \sin x,$ todos$y$ los valores se multiplicarán por 2 y la amplitud de la función será$2 .$ La gráfica para$y=2 \sin x$ se muestra en la página siguiente.

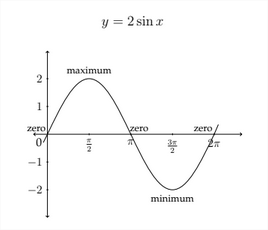
$clipboard_e10addc6d6e9fb4f730cea8eb2beb47da.png$
Un valor negativo del coeficiente frente a una función trigonométrica no cambiará la Amplitud de la función, sino que cambiará la forma de la función. Por ejemplo, la función:
tiene una amplitud de$1,$ pero la gráfica será diferente de la gráfica$y=\sin x$ Todos los$y$ -valores de la función$y=-\sin x$ tendrán el signo opuesto como los$y$ -valores de la función$y=\sin x .$ La gráfica para$y=-\sin x$ aparece abajo:
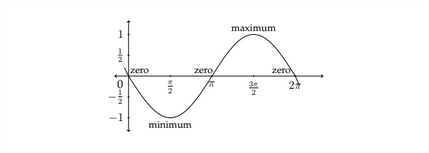
$clipboard_e649a25a6314b95e2bb5ea5f252ee379a.png$
Observe que, debido a la negación de los$y$ -valores, la gráfica comienza en$0,$ como lo hace la función sinusoidal estándar, pero la gráfica de$y=-\sin x$ primero va a un valor mínimo antes de cruzar por 0 nuevamente hasta el valor máximo.

De igual manera, la gráfica de$y=-\cos x$ comienza en el valor mínimo antes de cruzar por 0 e ir al valor máximo, volver a través de 0 y terminando en el valor mínimo nuevamente.

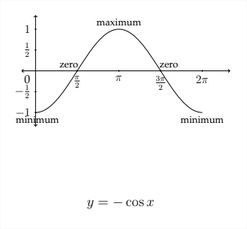
$clipboard_eb2800d610ad544d5ea48a970891bd43a.png$

Periodo
El periodo de la gráfica se refiere al tiempo que tarda la gráfica en completar un ciclo completo de valores. En las funciones estándar de seno y coseno, el período es$2 \pi$ radianes. La función completa una sola “onda” y vuelve a su lugar inicial entre 0 y$2 \pi .$ un coeficiente delante de la variable en una función sinusoidal o coseno afectará el periodo de la gráfica. En la expresión general$y=A \sin B x,$ el valor de$A$ afecta la amplitud de la función y el valor de$B$ afecta el periodo de la función.

Si examinamos la tabla de valores para la función sinusoidal estándar, podemos ver cómo afectará el coeficiente de la$x$ variable -al periodo de la gráfica. Comenzando con la tabla de la función sinusoidal estándar:

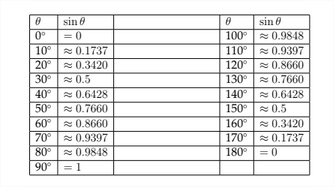
$clipboard_e6529e99371cc5c0ad4407afcb59ae469.png$

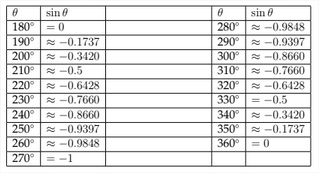
$clipboard_ed9db336957eb1992d191ce40715e87cd.png$

Si creamos una tabla similar para la función$y=\sin (2 x),$ entonces podemos ver cómo esto afectará a la gráfica:

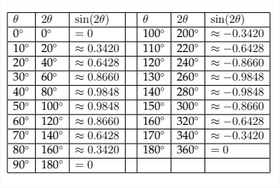
$clipboard_ee42dab72e931f24237f8763d496e1961.png$

En la tabla anterior podemos ver que la función$y=\sin (2 x)$ completa un ciclo completo entre 0 y$\pi$ radianes en lugar del estándar 0 a$2 \pi$ radianes. A continuación se muestra la gráfica para estos puntos. También se muestran las coordenadas para$x$ los valores -entre
$\pi$ y$2 \pi$ radianes.

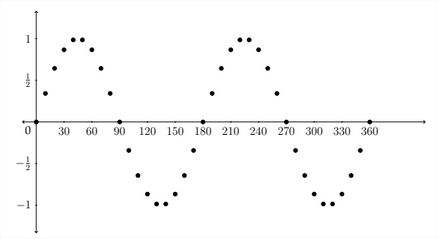
$clipboard_e718e7dfec6f34d305284574e705e3ff5.png$

En esta gráfica, se puede ver que hay dos ondas completas entre 0 y$2 \pi$ radianes, o una onda completa entre 0 y$\pi$ radianes. Entonces, en una función sinusoidal o coseno de la forma$y=A \sin B x,$ la amplitud será$|A|$ y el periodo será$\frac{2 \pi}{b} .$ La gráfica estándar para un ciclo completo de la función$y=\sin (2 x)$ se muestra a continuación:
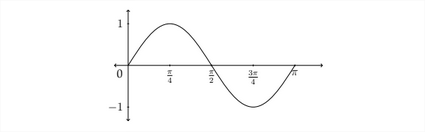
$clipboard_e1acf6e221a60970c0ef974e75863c921.png$
Observe que, debido a que el periodo se ha cortado a la mitad, el $x$-coordenadas que corresponden a los$y$ coondinatos máximo, mínimo y cero se cortan a la mitad como

Ejemplo 1
Graficar un periodo completo de la función$y=-2 \sin 3 x$
La amplitud en este caso es$2,$ pero como el coeficiente es negativo, esta gráfica sinusoidal comenzará yendo primero al valor mínimo. El periodo de la gráfica será$\frac{2 \pi}{B},$ o en este caso en$\frac{2 \pi}{3}$ lugar de$2 \pi .$ Para determinar los$x$ valores -para los valores máximo, mínimo y cero$y$ -valores, debemos examinar cómo se determinan estos para la curva sinusoidal estándar.

Los valores y máximo, mínimo y cero para una curva sinusoidal estándar ocurren en los ángulos cuadrangulares, es decir, los ángulos que separan los cuatro cuadrantes entre sí. Los ángulos cuadránticos son 0 'o 0 radianes,$90^{\circ}$ o$\frac{\pi}{2}$ radianes,$180^{\circ}$ o radianes\ pi,$270^{\circ}$ o$\frac{3 \pi}{2}$ radianes$360^{\circ}$ y/o$2 \pi$ radianes. Estos$x$ valores producen los valores “críticos” y del cero, máximo y mínimo.

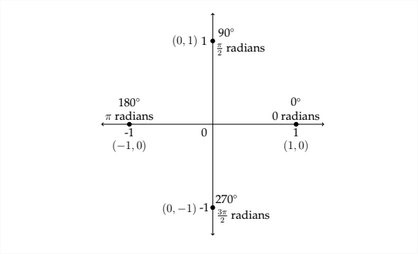
$clipboard_eb1b0ec8e5ccf9fe176fd73368f4cae7b.png$

En la gráfica estándar de seno o coseno, la distancia desde cada “valor crítico” del

gráfico a la siguiente es siempre un “salto” de$\frac{\pi}{2}$ a lo largo del$x$ eje -. Esto es una cuarta parte del periodo:$\frac{2 \pi}{1} * \frac{1}{4}=\frac{\pi}{2} .$ Entonces, para determinar las etiquetas para los valores críticos de la gráfica a lo largo del$x$ eje, debemos tomar el nuevo periodo y multiplicar por$\frac{1}{4}$

La función con la que estamos trabajando es$y=-2 \sin 3 x,$ así encontrar el nuevo periodo$\frac{2 \pi}{B},$ que calculamos que era$\frac{2 \pi}{3} .$ Entonces, para etiquetar correctamente el$x$ eje -debemos tomar$\frac{2 \pi}{3}$ y multiplicar por$\frac{1}{4}$
\ [ \ frac {2\ pi} {3} *\ frac {1} {4} =\ frac {2\ pi} {12} =\ frac {\ pi} {6}
\] Entonces, los valores críticos a lo largo del$x$ eje -serán:
\ [\ frac {1\ pi} {6},\ frac {2\ pi} {6},\ frac {3\ pi} {6},\ text {y}\ frac {4\ pi} {6}
\] Queremos expresarlos en términos más bajos, así los etiquetaríamos como$\frac{\pi}{6}, \frac{\pi}{3}, \frac{\pi}{2},$ y$\frac{2 \pi}{3} .$ La gráfica comenzará en cero, entonces (debido a que el valor del coeficiente$A$ es negativo) bajará a un valor mínimo$\frac{\pi}{6},$ atrás a cero en$\frac{\pi}{3},$ entonces hasta el máximo at$\frac{\pi}{2}$ y retrocederá a cero en$\frac{2 \pi}{3}$ para completar un periodo completo de la gráfica. La gráfica de esta función se muestra a continuación. Observe que el valor y mínimo es -2 y el$y$ valor -máximo es 2 porque$A=2$
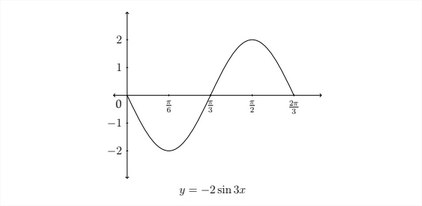
$clipboard_e67301b047c0b60305317f8095cae63a5.png$
Veamos un ejemplo usando la gráfica coseno.

Ejemplo 2
Gráfica un periodo completo de$y=5 \cos \frac{2}{3} x$
la función La amplitud de la función es 5 porque$A=5,$ así el valor y máximo será 5 y el$y$ valor mínimo será$-5 .$ El periodo de la gráfica será el$\frac{2 \pi}{B}$ cual en este caso es$\frac{2 \pi}{7}=2 \pi * \frac{3}{2}=3 \pi .$ Así el periodo es 3$\pi .$ Los valores críticos a lo largo$x$ del eje -comenzarán en 0 y estarán separados por “saltos” de$3 \pi * \frac{1}{4}=\frac{3 \pi}{4} .$ Así que los valores críticos a lo largo$x$ del eje serán:
\ [ 0,\ frac {3\ pi} {4},\ frac {6\ pi} {4},\ frac {9\ pi} {4},\ text {y}\ frac {12\ pi} {4}
\] Queremos expresarlos en términos más bajos para que los etiquetemos como$\frac{3 \pi}{4}, \frac{3 \pi}{2}, \frac{9 \pi}{4}$ y$3 \pi .$ La gráfica comenzará en el$y$ valor máximo de 5 en$x=0,$ luego irá a cero en$x=\frac{3 \pi}{4},$ abajo al mínimo$y$ -valor de -5$x=\frac{3 \pi}{2},$ atrás a través de 0 at$x=\frac{9 \pi}{4},$ y luego hasta el$y$ valor máximo de 5 at$x=3 \pi$ para completar un periodo completo de la gráfica. La gráfica de$y=5 \cos \frac{2}{3} x$. se muestra a continuación.

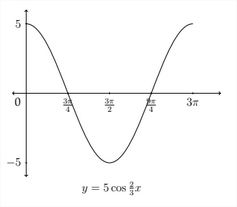
$clipboard_e9162d65c3cd1ee96c71269b0d848fda1.png$

Determinar una ecuación a partir de una gráfica
A veces, se le dará una gráfica y se le pedirá que determine una ecuación que satisfaga las condiciones visibles en la gráfica. Hasta el momento, solo hemos discutido dos de las posibles transformaciones de una función trigonométrica: la amplitud y el período. Recuerda que en una ecuación de la forma$y=A \sin B x$ o$y=A \cos B x,$ la amplitud es$|A|$ y el periodo es$\frac{2 \pi}{B} .$ Así, para escribir una ecuación para una función trigonométrica, necesitamos determinar los valores de$A$ y$B$.
Ejemplo 3

Deterimine una ecuación que satisfaga la gráfica dada.
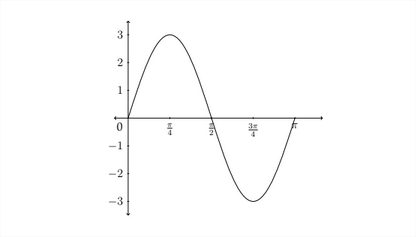
$clipboard_ee9c8a3fe37f39fe18fb601c1dc85f4c6.png$
Primero tenga en cuenta que el$y$ -valor máximo para la gráfica es 3 y el mínimo es -3 Esto significa que la amplitud es$3 .$ A continuación vemos que hay un periodo completo de la función entre 0 y$\pi$, esto significa que el periodo es$\pi$. A partir de esta información, sabemos que$A=3$ y que el periodo para la gráfica es$\pi$. Desde el periodo$P=\frac{2 \pi}{B},$ entonces sabemos que$B=\frac{2 \pi}{P} .$ Así,$B=\frac{2 \pi}{\pi}=2$

Por último, esta gráfica comienza con un$y$ -valor del$5,$ cual es el$y$ valor máximo. Luego va a 0 y baja al mínimo, de vuelta a través de 0 y luego de vuelta al máximo para formar una onda completa. ya que esta es la firma de la función coseno, la respuesta a este problema sería:
\ [ y=5\ cos\ frac {8} {9} x
\]

Ejercicios 2.2
Determinar la amplitud y el periodo para cada problema y graficar un periodo de la función. Identificar puntos importantes en los$y$ ejes$x$ y.
1. $y=\cos 4 x$
2. $y=-\sin 2 x$
3. $y=3 \sin 3 x$
4. $y=-2 \cos 5 x$
5. $y=4 \cos \frac{1}{2} x$
6. $y=2 \sin \frac{1}{3} x$
7. $y=-\frac{1}{2} \sin \frac{2}{3} x$
8. $y=-3 \cos \frac{1}{5} x$
9. $y=-4 \sin 6 x$
10. $y=3 \sin 4 x$
11. $\quad y=2 \cos \frac{1}{2} x$
12. $\quad y=3 \cos \frac{1}{3} x$
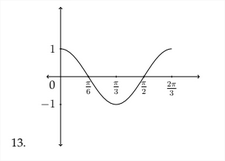
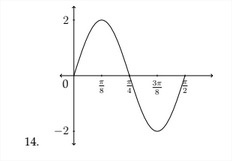
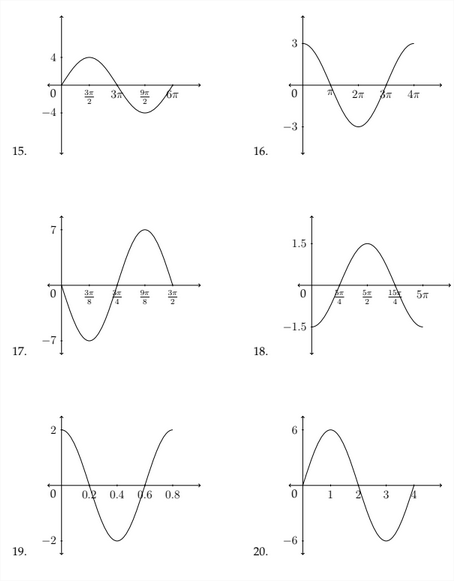
Determinar una ecuación que sacifique la gráfica dada.

$clipboard_eab715513ed7308128d01ae2d789f5531.png$ $clipboard_ec092dcd152289cb4b73d358937de9c6b.png$

$clipboard_e432b94b1a3bdf90344b42614ce0df8a3.png$