2.5: Combinando las Transformaciones
- Page ID
- 117035
En los apartados anteriores, hemos visto cómo las diversas transformaciones actúan sobre las funciones trigonométricas y hemos trabajado con las tres primeras (amplitud, periodo y desplazamiento vertical) en combinación entre sí. Combinar el cambio de fase con las otras transformaciones es complicado debido a la forma en que el período y el desplazamiento de fase interactúan entre sí.
Ahora tenemos dos ecuaciones estándar para la sinusoide:
\ [
Y=A\ sin (B x+C) +D
\]
y
\ [
y=A\ cos (B x+C) +D
\]
\(A\) y\(D,\) la amplitud y el desplazamiento vertical afectan al\(y\) eje -, mientras\(B\) y\(C\) afectar al\(x\) eje -.

Veamos un ejemplo en el que necesitamos combinar un cambio en el periodo de la gráfica con un desplazamiento de fase.
Ejemplo 1
Grafica al menos un periodo de la función dada. Indicar los valores importantes a lo largo de los\(y\) ejes\(x\) y.
\(y=\cos (4 x+\pi)\)
Las transformaciones en este ejemplo solo afectan al\(x\) eje -eje. El periodo de la función es\(\frac{2 \pi}{B}=\frac{2 \pi}{4}=\frac{\pi}{2} .\) Así, la función completará un ciclo completo sobre una distancia de\(\frac{\pi}{2}\) a lo largo del\(x\) eje -eje.
No obstante, debido al desplazamiento de fase, esta gráfica no comenzará en 0 y terminará en\(\frac{\pi}{2} .\) Necesitamos encontrar el nuevo punto de partida que es causado por el desplazamiento de fase. Entonces, tomamos lo que se llama el “argumento”, o lo que es lo que estamos encontrando el coseno de:\((4 x+\pi)\) y fijamos eso igual a cero.
\ [
\ begin {array} {c}
4 x+\ pi=0\\
4 x=-\ pi\\
x=-\ frac {\ pi} {4}
\ end {array}
\]
Este es nuestro nuevo punto de partida. Para identificar los valores críticos a lo largo del\(x\) eje, necesitaremos determinar hasta qué punto se le\(^{\prime \prime}\) daría a cada “salto un periodo de\(\frac{\pi}{2}\)
\ [
\ frac {\ pi} {2} *\ frac {1} {4} =\ frac {\ pi} {8}
\]
Entonces, cada valor crítico posterior a lo largo del\(x\) eje -será estar a una\(\frac{\pi}{8}\) distancia de la anterior. Si empezamos en nuestro nuevo punto de partida para esta función\(-\frac{\pi}{4},\) entonces si sumamos\(\frac{\pi}{8}\) un total de 4 veces, llegaremos a cada uno de los cinco valores críticos para esta función.
Entonces, cada valor crítico posterior a lo largo del\(x\) eje -será una\(\frac{\pi}{8}\) distancia del anterior. Si comenzamos en nuestro nuevo punto de partida para esta función\(-\frac{\pi}{4},\) entonces si agregamos\(\frac{\pi}{8}\) un total de 4 veces, llegaremos a cada uno de los cinco valores críticos para esta función
\ [
\ begin {array} {c}
-\ frac {\ pi} {4} +\ frac {\ pi} {8} =-\ frac {2\ pi} {8} +\ frac {\ pi} {8} =-\ frac ac {\ pi} {8}\ \
-\ frac {\ pi} {8} +\ frac {\ pi} {8} =0\\
0+\ frac {\ pi} {8} =\ frac {\ pi} {8}\
\ frac {\ pi} {8} +\ frac {\ pi} {8} =\ frac {2\ pi} {8} =\ frac {\ pi} 4}
\ end {array}
\]
Así que los valores críticos a lo largo del\(x\) eje serían:
\ [
-\ frac {\ pi} {4}, -\ frac {\ pi} {8}, 0,\ frac {\ pi} {8},\ text {y}\ frac {\ pi} {4}
\]
Observe que la distancia entre el punto inicial\(-\frac{\pi}{4}\) y el punto final\(\frac{\pi}{4}\) es igual al periodo que encontramos al inicio del problema, que fue\(\frac{\pi}{2} .\) Ahora vamos a graficar la función:
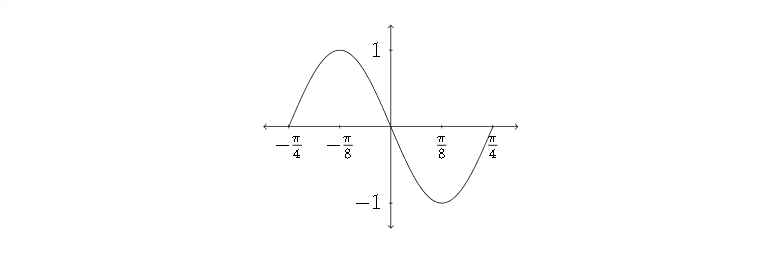
ya que no hubo cambios en el\(y\) eje -la amplitud para la función es 1 y el desplazamiento vertical es 0. A lo largo del\(x\) eje, vemos una función sinusoidal positiva que inicia\(\operatorname{at}\left(-\frac{\pi}{4}, 0\right)\) luego sube para\(\left(-\frac{\pi}{8}, 1\right),\) retroceder a través de (0,0) hasta\(\left(\frac{\pi}{8},-1\right)\) y retroceder\(\left(\frac{\pi}{4}, 0\right)\) hasta completar un ciclo completo de la gráfica.
Veamos un ejemplo en el que hay algunos cambios tanto en el\(y\) eje -como en el\(x\) eje -.
Ejemplo 2
Grafica al menos un periodo de la función dada. Asegúrese de identificar valores críticos a lo largo de los\(y\) ejes\(x\) y.
\ [
y=-\ frac {5} {2} +\ cos (3 x-\ pi)
\]
Recuerda qué coeficientes afectan a qué eje en la gráfica:

En este ejemplo, la amplitud es\(1,\) ya que no hay coeficiente frente a la función coseno. El desplazamiento vertical es el\(-\frac{5}{2},\) que desplazará la función hacia abajo una distancia de 2.5 en el\(y\) eje -axis. Entonces, los puntos de línea media o “cero” de la gráfica estarán en\(-2.5,\) el\(y\) valor máximo será de -1.5 y el\(y\) valor mínimo será de -3.5
A lo largo del\(x\) eje -el periodo para la gráfica será\(\frac{2 \pi}{B}=\frac{2 \pi}{3},\) ya que el coeficiente\(B\) en este problema es\(3 .\) Para encontrar el nuevo punto de partida, tomaremos el argumento de la función coseno y lo pondremos igual a cero.
\ [
\ begin {array} {c}
3 x-\ pi=0\\
3 x=\ pi\\
x=\ pi *\ frac {1} {3} =\ frac {\ pi} {3}
\ end {array}
\]
Entonces, nuestro nuevo punto de partida estará en\(\frac{\pi}{3} .\) Para determinar los otros valores críticos a lo largo del\(x\) eje, podemos averiguar hasta qué punto estaría cada “salto” entre los valores críticos. Para ello, tomamos el periodo\(\left(\frac{2 \pi}{3}\right)\) y lo dividimos por 4 (o multiplicamos por
\(\left.\frac{1}{4}\right)\)
\ [
\ frac {2\ pi} {3} *\ frac {1} {4} =\ frac {2\ pi} {12} =\ frac {\ pi} {6}
\]
Ahora podemos agregar este valor a nuestro nuevo punto de partida cuatro veces para determinar el otro crítico valores a lo largo del\(x\) eje.
\ [
\ begin {array} {c}
\ frac {\ pi} {3} +\ frac {\ pi} {6} =\ frac {2\ pi} {6} +\ frac {\ pi} {6} =\ frac {3\ pi} {6} =\ frac {\ pi} {2}\
\ frac {3\ pi} {6} +\ frac {\ pi} {6} =\ frac {4\ pi} {6} =\ frac {2\ pi} {3}\
\ frac {4\ pi} {6} +\ frac {\ pi} {6} =\ frac {5\ pi} {6}\
\ frac {5\ pi} {6} +\ frac {\ pi } {6} =\ pi
\ end {array}
\]
Así que los valores críticos a lo largo\(x\) del eje serían:
\ [\ frac {2\ pi} {6},\ frac {3\ pi} {6},\ frac {4\ pi} {6},\ frac {5\ pi} {6},\ text {y}\ frac {6\ pi} {6}
\] [
\ begin {array} {c}
\ texto {o} \
\ frac {\ pi} {3},\ frac {\ pi} {2},\ frac {2\ pi} {3},\ frac {5\ pi} {6},\ text {y}\ pi
\ end {array}
\]
Nuevamente, observe que la distancia a lo largo del\(x\) eje -desde el punto inicial hasta el punto final es el punto:\(\frac{2 \pi}{3} .\) Ahora vamos a graficar la función:
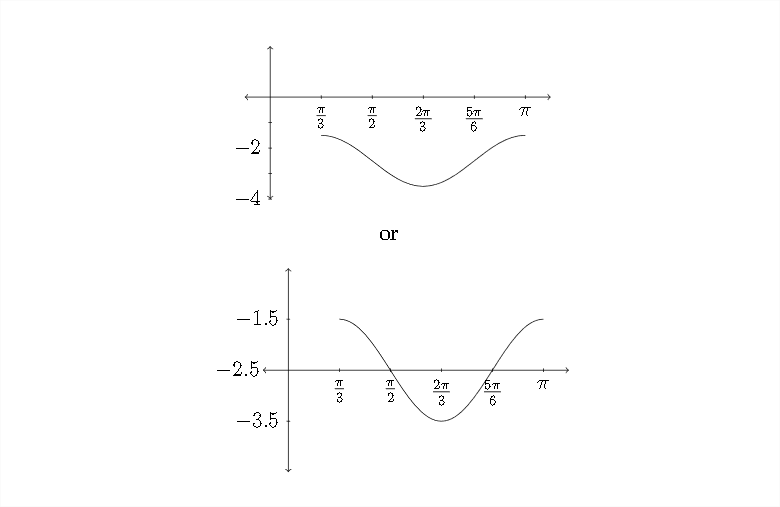
Veamos un ejemplo más.
Ejemplo 3
A veces el coeficiente\(B\) aparece factorizado fuera del argumento como lo hace en el problema de abajo.
Grafique al menos un periodo de la función dada. Asegúrese de incluir los valores críticos a lo largo de los\(y\) ejes\(x\) y.
\(y=4 \sin 2\left(x+\frac{\pi}{3}\right)-1\)
Primero veamos cómo los\(y\) ejes\(x\) y se ven afectados por las transformaciones en este problema.

\ [
y=4\ sin 2\ left (x+\ frac {\ pi} {3}\ right) -1
\]
La amplitud en este problema es 4 y el desplazamiento vertical es -1
El periodo para esta gráfica es\(\frac{2 \pi}{B}=\frac{2 \pi}{2}=\pi .\) Observe que el valor de\(B\) es 2 en este ejemplo, aunque haya sido factorizado del resto del argumento.
El nuevo punto de partida para la gráfica es en realidad más fácil de encontrar en problemas de este tipo. Si tomamos el argumento tal como es y lo ponemos igual a cero:
\ [
2\ left (x+\ frac {\ pi} {3}\ right) =0
\]
podemos dividir a través de ambos lados por 2 para cancelar el factor de\(B\):
\ [
\ begin {array} {c}
\ frac {2\ left (x+\ frac {\ pi} {3}\ right)} {2} =\ frac {0} {2}\\
x+\ frac {\ pi} {3} =0\\
x=-\ frac {\ pi} {3}
\ end {array}
\]
Entonces, el nuevo punto de partida para la función es\(-\frac{\pi}{3}\)
Ahora vamos a encontrar el resto de los valores críticos a lo largo del\(x\) eje -eje. El periodo para esta gráfica es\(\pi,\) así que el “salto" entre los valores críticos a lo largo del\(x\) eje -será:
\ [
\ pi *\ frac {1} {4} =\ frac {\ pi} {4}
\]
Para encontrar el resto de los valores críticos tendremos que sumar\(\left(-\frac{\pi}{3}\right)\) cuatro veces\(\frac{\pi}{4}\) al punto de partida de la gráfica:
\ [
\ begin {array} {c}
-\ frac {\ pi} {3} +\ frac {\ pi} {4} =-\ frac {4\ pi} {12} +\ frac {3\ pi} {12} =-\ frac {\ pi} {12}\
-\ frac {\ pi} {12} +\ frac {3\ pi} {12} = \ frac {2\ pi} {12} =\ frac {\ pi} {6}\
\ frac {2\ pi} {12} +\ frac {3\ pi} {12} =\ frac {5\ pi} {12}\
\ frac {5\ pi} {12} +\ frac {3\ pi} {12} =\ frac {8\ pi} 12} =\ frac {2\ pi} {3}
\ end {array}
\]
Así que los valores críticos a lo largo del\(x\) eje serían:
\ [
-\ frac {4\ pi} {12}, -\ frac {1\ pi} {12},\ frac {2\ pi} {12},\ frac {5\ pi} {12},\ text {y}\ frac {8\ pi} {12}
\]
O
\ [
-\ frac {\ pi} {3}, -\ frac {\ pi} {12},\ frac {\ pi} {6},\ frac {5\ pi} {12},\ texto {y}\ frac {2\ pi} {3}
\]
Ahora que hemos abordado cada una de las cuatro transformaciones usemos esta información para dibujar la gráfica. Primero el\(y\) -eje - la amplitud es 4 y el desplazamiento vertical es -1:
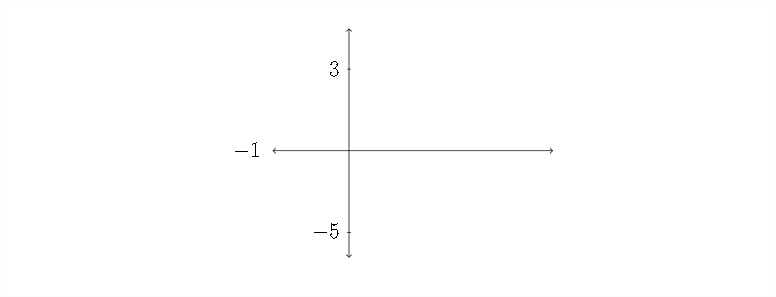
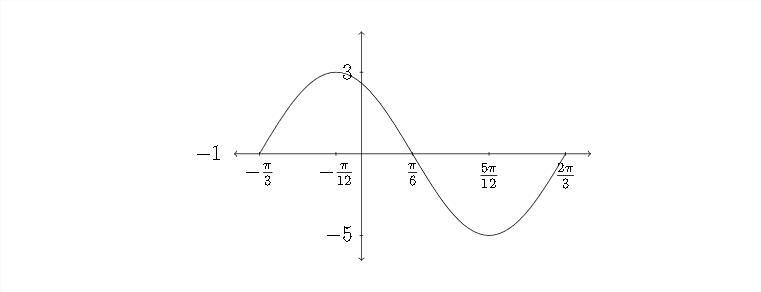
Ahora, vamos a rellenar la información para el\(x\) eje -. Los valores críticos a lo largo del\(x\) eje\(\operatorname{are}-\frac{\pi}{3},-\frac{\pi}{12}, \frac{\pi}{6}, \frac{5 \pi}{12},\) y\(\frac{2 \pi}{3}\)
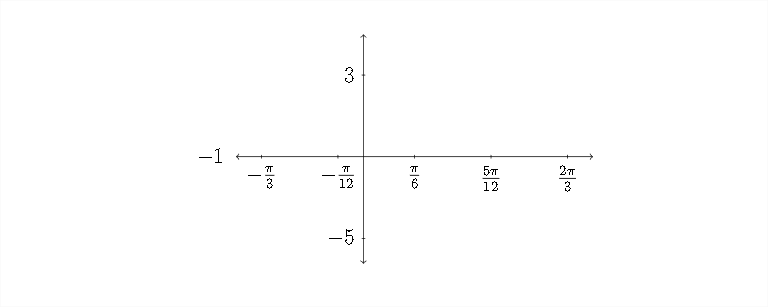
La función que estamos graficando es una función sinusoidal positiva, por lo que comenzará en la “línea media” o valor cero (que en este caso es -1), irá hasta el máximo, de vuelta por la línea media al mínimo y de vuelta a la línea media:
Determine la Amplitud, Período, Desplazamiento Vertical y Desplazamiento de Fase para cada función y grafique al menos un periodo completo. Asegúrese de identificar los valores críticos a lo largo de los\(y\) ejes\(x\) y.
1. \(\quad y=\sin \left(x+\frac{\pi}{2}\right)\)
2. \(\quad y=\sin (x-\pi)\)
3. \(\quad y=3 \cos \left(x-\frac{\pi}{2}\right)\)
4. \(y=\frac{1}{2} \cos (x+\pi)\)
5. \(\quad y=3+\cos \left(x-\frac{\pi}{4}\right)\)
6. \(\quad y=-2+\sin \left(x+\frac{\pi}{6}\right)\)
7. \(\quad y=\sin (2 x-\pi)\)
\(8 . \quad y=\sin \left(4 x+\frac{\pi}{4}\right)\)
\(9 . \quad y=2 \cos \left(\frac{x}{2}+\pi\right)\)
\(10 . \quad y=-3 \sin (6 x-\pi)\)
11. \(y=-\frac{1}{3} \sin \left(2 x+\frac{\pi}{4}\right) \quad\)
12. \(\quad y=\frac{1}{2} \cos \left(\frac{x}{2}-\pi\right)\)
13. \(\quad y=2 \sin \left(2 x-\frac{\pi}{3}\right)-1\)
\(14 . \quad y=1+2 \cos \left(3 x+\frac{\pi}{2}\right)\)
15. \(\quad y=3 \cos 2\left(x+\frac{\pi}{6}\right)\)
16. \(\quad y=-4 \sin 2\left(x+\frac{\pi}{2}\right)\)
\(17 . \quad y=\sin \frac{1}{2}\left(x+\frac{\pi}{4}\right)\)
18. \(\quad y=3+2 \sin 3\left(x+\frac{\pi}{2}\right)\)
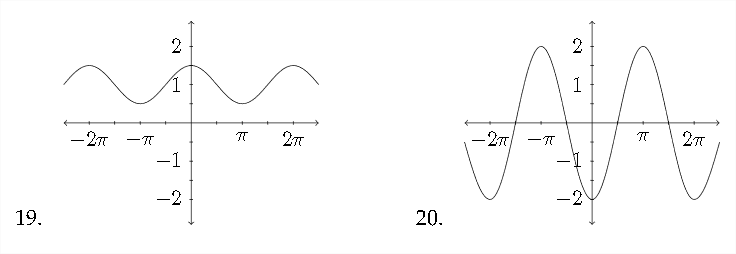
En problemas\(19-22,\) determinar una ecuación para la función que se muestra.
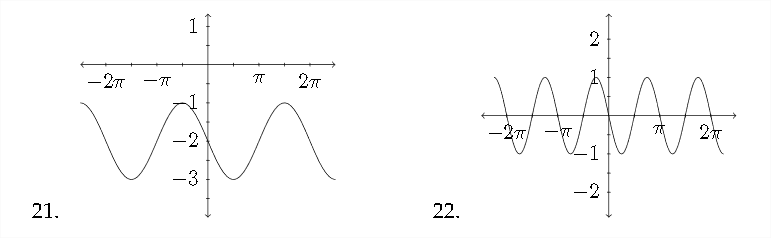
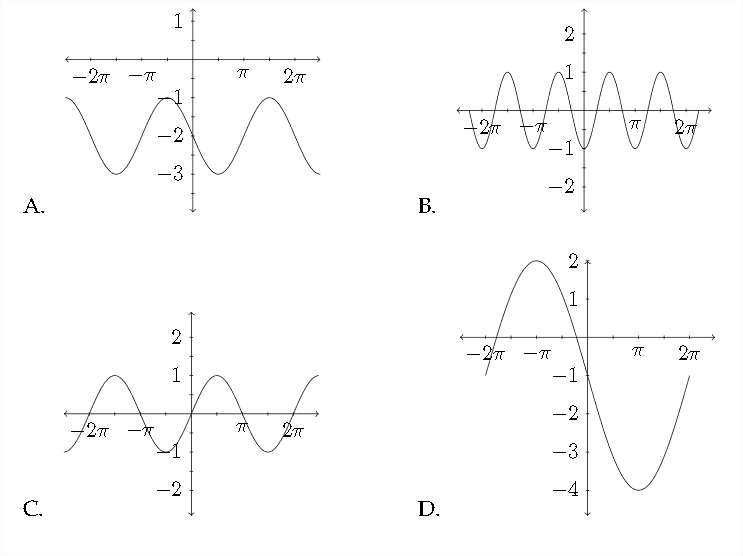
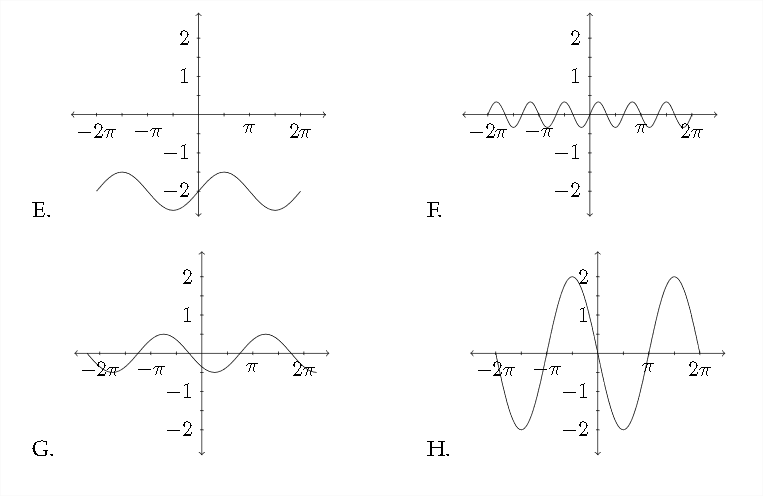
Coincidir la función con la gráfica apropiada
23. \(\quad y=-\cos 2 x\)
24. \(\quad y=\frac{1}{2} \sin x-2\)
25. \(\quad y=2 \cos \left(x+\frac{\pi}{2}\right)\)
26. \(\quad y=-3 \sin \frac{1}{2} x-1\)
27. \(\quad y=\sin (x-\pi)-2\)
28. \(\quad y=-\frac{1}{2} \cos \left(x-\frac{\pi}{4}\right)\)
29. \(\quad y=\frac{1}{3} \sin 3 x\)
30. \(\quad y=\cos \left(x-\frac{\pi}{2}\right)\)
Determine la Amplitud, Período, Desplazamiento Vertical y Desplazamiento de Fase para cada función y grafique al menos un periodo completo. Asegúrese de identificar los valores críticos a lo largo de los\(y\) ejes\(x\) y.
31. \(\quad y=2 \cos \left(2 x+\frac{\pi}{2}\right)-1\)
32. \(\quad y=-4 \cos (3 x-2 \pi)\)
33. \(\quad y=\sin \left(2 x-\frac{\pi}{4}\right)\)
\(34 . \quad y=-\sin (3 x+\pi)\)
35. \(\quad y=3 \cos \left(x+\frac{\pi}{3}\right)+1\)
36. \(\quad y=-2 \sin \left(3 x-\frac{\pi}{2}\right)+4\)
37. \(\quad y=-\frac{1}{2} \sin \left(x-\frac{\pi}{2}\right)-2\)
38. \(\quad y=2-\cos \left(2 x-\frac{\pi}{3}\right)\)


