2.4: Desplazamiento de fase

Última actualización
Guardar como PDF

Page ID: 117028

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

La última forma de transformación que discutiremos en la gráfica de las funciones trigonométricas es el desplazamiento de fase, o desplazamiento horizontal. Hasta el momento, hemos considerado las transformaciones de amplitud, periodo y desplazamiento vertical de las funciones trigonométricas. En la ecuación estándar$y=A \sin (B x)+D,$ estos corrresponden a los coeficientes$A, B$ y$D .$ Observe que los coeficientes de amplitud y desplazamiento vertical$(A \text { and } D),$ que afectan al$y$ eje se producen fuera de la función trigonométrica, mientras que el coeficiente que afecta el periodo de la gráfica a lo largo del$x$ eje -ocurre dentro de la función sinusoidal. Esto también es cierto para el cambio de fase.
Si consideramos una ecuación general de:
\ [ Y=A\ sin (B x+C) +D
\] la constante$C$ afectará al desplazamiento de fase, o desplazamiento horizontal de la función. Veamos un ejemplo sencillo.

Grafique al menos un periodo de la función dada:$\quad y=\sin (x+\pi)$ Asegúrese de indicar puntos importantes a lo largo de$y$ los ejes$x$ y.
Examinemos esta función mirando una tabla de valores.
$clipboard_eea838b016f267b5815be7961be0f71cd.png$

Ahora veamos una gráfica de en$y=\sin (x+\pi)$ comparación con la gráfica estándar de$y=\sin x$

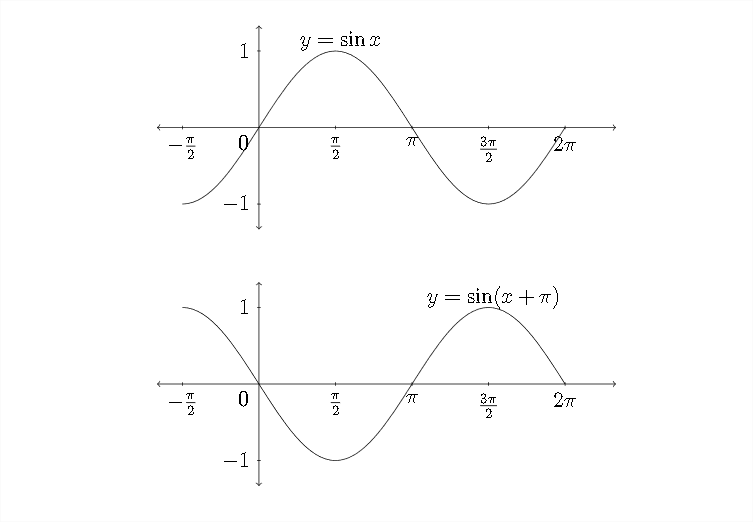
$clipboard_ea97568fc29ad3b695c44e798e3a63cb4.png$

Observe que si tomamos la gráfica estándar de$y=\sin x$ y la arrastramos hacia atrás a lo largo del$x$ eje -eje una distancia de$\pi,$ tendríamos la gráfica de$y=\sin (x+\pi)$ Eso es porque cada$x$ valor se le$\pi$ ha agregado, así que para llegar al$x$ valor que produce un particular $y$-valor, necesitaríamos restar$\pi$. Aquí hay un ejemplo:

$clipboard_eafd6029e16e02557d6bd444bbcdec9f2.png$

En la tabla anterior vemos el estándar$x$ y$y$ los valores para la gráfica de la función sinusoidal. En la siguiente tabla, agregamos una columna que muestra el valor que$x$ tendría que ser$x+\pi$ para ser los valores estándar:

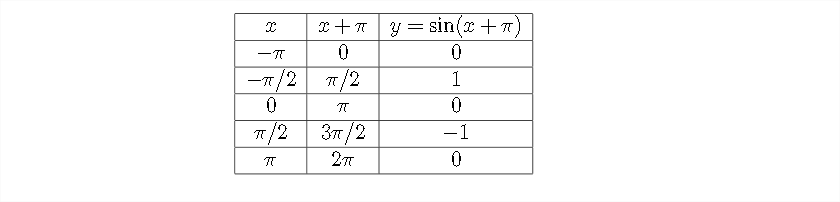
$clipboard_e05ce85703e45666c62b4cfea8cf799fa.png$

Aquí hay una gráfica de estos valores:

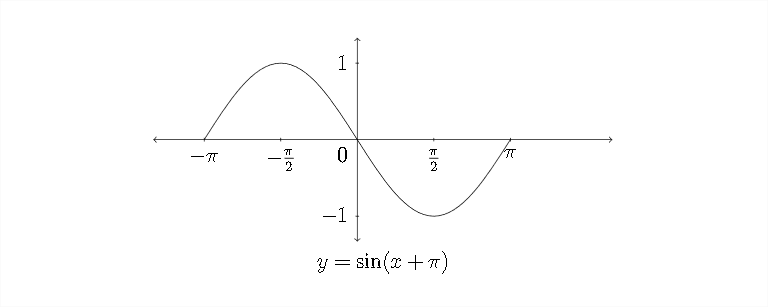
$clipboard_e95f548b13685dffd12f70d8af31280de.png$

Esta es la misma gráfica de la$y=\sin (x+\pi)$ que vimos en la página anterior, pero anclada a diferentes puntos en el$x$ eje -eje. Cualquiera de los dos gráficos sería una respuesta correcta a una pregunta que pide por lo menos un periodo de la gráfica de$y=\sin (x+\pi)$
Veamos otro ejemplo:

Ejemplo 2
Grafique al menos un periodo de la función dada:$y=\sin \left(x+\frac{\pi}{3}\right)$ Asegúrese de indicar puntos importantes a lo largo de$y$ los ejes$x$ y.
En este ejemplo simplificado, realmente solo tenemos una transformación de la que preocuparnos: el cambio de fase. Observe que la amplitud, el periodo y el desplazamiento vertical se han dejado fuera. Al considerar una gráfica de seno o coseno que tenga un desplazamiento de fase, una buena manera de iniciar la gráfica de la función es determinar el nuevo punto de partida de la gráfica. En el ejemplo anterior, vimos cómo la función$y=\sin (x+\pi)$

desplazó la gráfica una distancia de$\pi$ a la izquierda e hizo el nuevo punto de partida de la curva sinusoidal$-\pi$

Al graficar la curva sinusoidal estándar generalmente nos interesan los ángulos cuadránticos que producen los puntos máximo, mínimo y cero de la gráfica. Al graficar la función$y=\sin \left(x+\frac{\pi}{3}\right),$ queremos saber qué valores de$x$ producirán los ángulos cuadránticos cuando los$\frac{\pi}{3}$ agreguemos.

Entonces, para determinar el nuevo punto de partida queremos conocer la solución a la ecuación$x+\frac{\pi}{3}=0$
\ [ \ qquad\ begin {array} {r}
x+\ frac {\ pi} {3} =0\\
-\ frac {\ pi} {3} -\ frac {\ pi} {3}\
x=-\ frac {\ pi} {3}
\ end {array}
\]

Este es el nuevo punto de partida para la gráfica$y=\sin \left(x+\frac{\pi}{3}\right) .$ Debido a que esta gráfica tiene un periodo estándar, el “salto” entre cada uno de los ángulos cuadránticos será
$\frac{\pi}{2} .$ Para graficar un periodo de una función trigonométrica típica necesitaremos al menos cinco valores de ángulo cuadrangular. Entonces, si nuestro nuevo punto de partida es$-\frac{\pi}{3}$, entonces el siguiente valor crítico a lo largo$x$ del eje -será:
\ [ -\ frac {\ pi} {3} +\ frac {\ pi} {2} =-\ frac {2\ pi} {6} +\ frac {3\ pi} {6} =\ frac {\ pi} {6}
\] Entonces los valores críticos subsiguientes serían:
\ [ \ begin {array} { c}
\ frac {\ pi} {6} +\ frac {\ pi} {2} =\ frac {\ pi} {6} +\ frac {3\ pi} {6} =\ frac {4\ pi} {6} =\ frac {2\ pi} {3}\
\ frac {4\ pi} {6} +\ frac {3\ pi} {6}} =\ frac {7\ pi} {6}\
\ frac {7\ pi} {6} +\ frac {3\ pi} {6} =\ frac {10\ pi} {6} =\ frac {5\ pi} {3}
\ end {array}
\]

Entonces los cinco valores críticos a lo largo del$x$ eje son:
\ [ -\ frac {2\ pi} {6},\ frac {\ pi} {6},\ frac {4\ pi} {6},\ frac {7\ pi} {6}\ text {y}\ frac {10\ pi} {6}
\] o, en forma reducida:
\ [ -\ frac {\ pi} {3},\ frac {\ pi} {6},\ frac {2\ pi} {3},\ frac {7\ pi} {6}\ texto {and}\ frac {5\ pi} {3}
\] Para graficar la función, pondríamos estos valores a lo largo del$x$ eje -y trazaríamos$y$ los valores cuadrantales estándar para que coincidan con ellos:

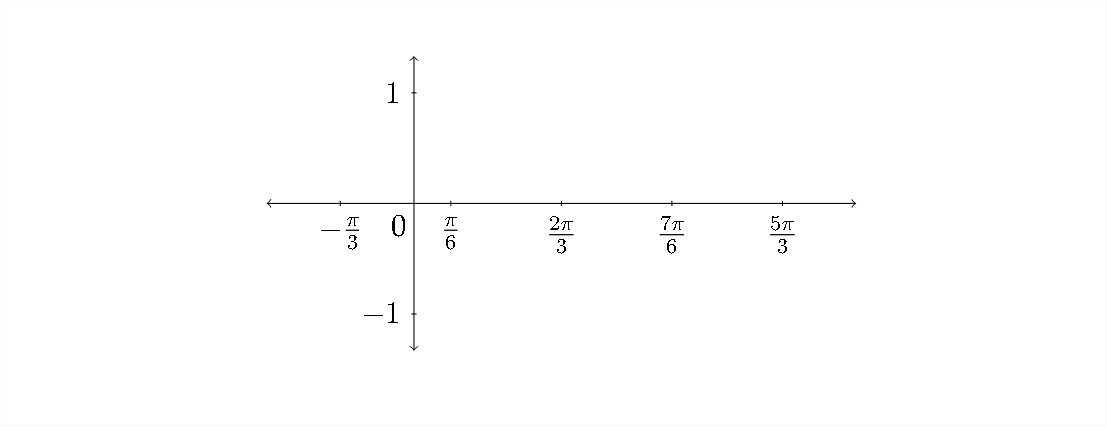
$clipboard_e7a2081f121713a784b96d06dec9e7796.png$

$y$Los valores -para la función sinusoidal comienzan en cero, suben al máximo, retroceden por cero al mínimo y luego vuelven a cero:

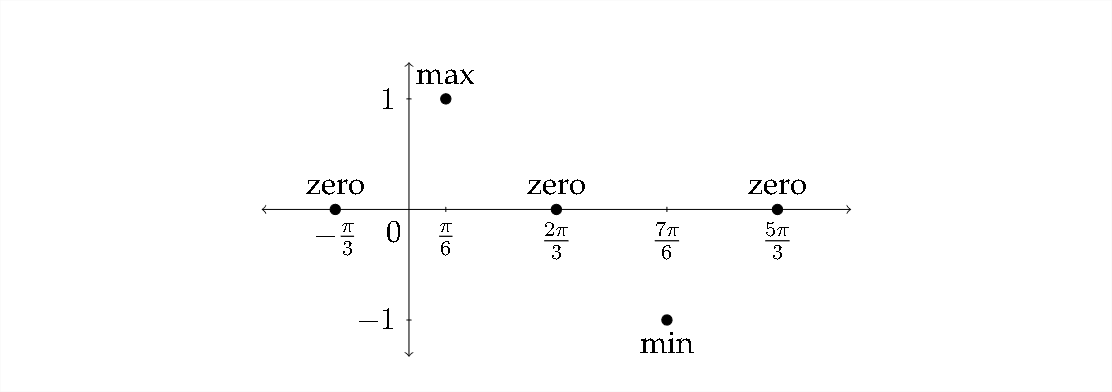
$clipboard_e6a3a76c56f36b6904e27204cc40f4294.png$

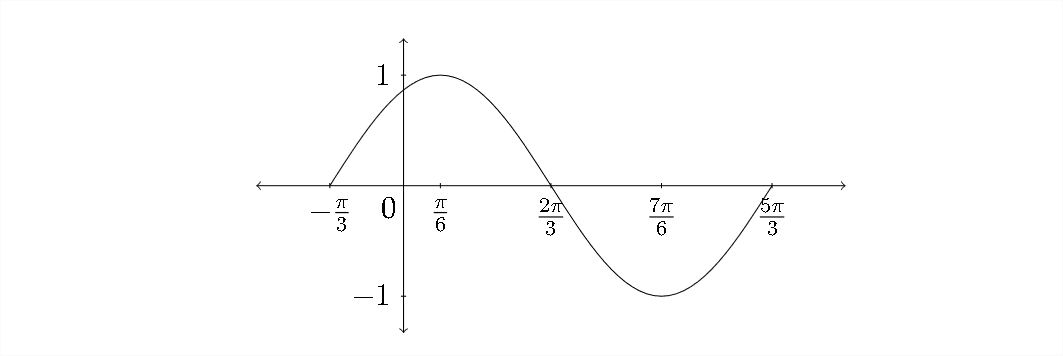
Conectando estos puntos para hacer una curva sinusoidal produce la siguiente gráfica:

$clipboard_efb0a49759e8bd757f4daf0701154e076.png$

Ejercicios 2.4
Emparejar cada función con la gráfica apropiada.
1. $\quad y=\cos \left(x-\frac{\pi}{4}\right)$
2. $\quad y=\sin \left(x+\frac{\pi}{4}\right)$
3. $\quad y=\cos x-1$
4. $\quad y=\sin x+1$
5. $\quad y=\sin \left(x-\frac{\pi}{4}\right)$
6. $\quad y=1-\cos x$
7. $\quad y=\sin x-1$
8. $\quad y=\cos \left(x+\frac{\pi}{4}\right)$

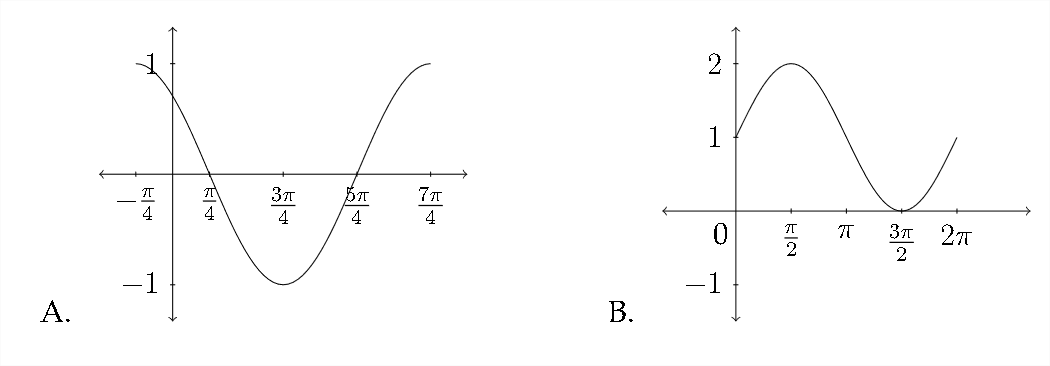
$clipboard_e1dd2353d5fa336008d23c08401f4509c.png$

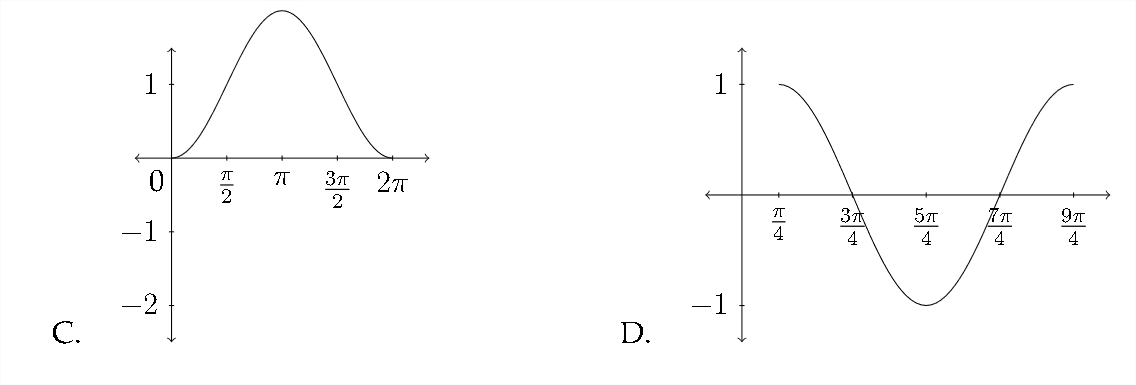
$clipboard_e9ff9ee4754f9eb6aace5fc83fee5040b.png$

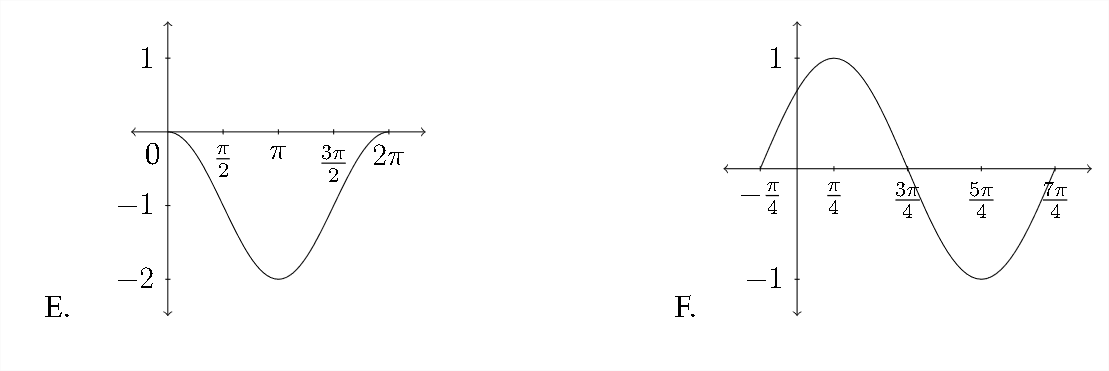
$clipboard_ee6a49a80cce1635f165c4124fa154b2c.png$

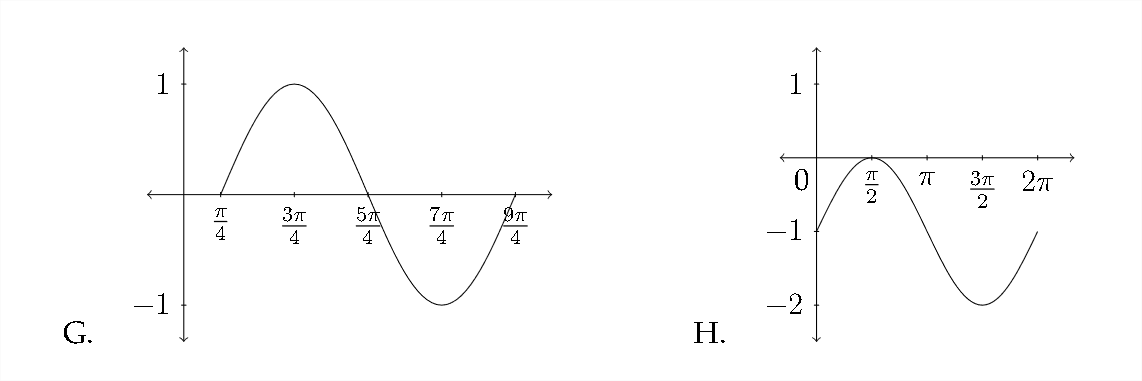
$clipboard_e94fb0d33b269c67405bd879e413c6069.png$

Haga un boceto de al menos un periodo para cada función. Asegúrese de incluir los valores importantes a lo largo de los$y$ ejes$x$ y.
9. $\quad y=\sin \left(x+\frac{\pi}{6}\right)$
$10 . \quad y=\cos \left(x-\frac{\pi}{6}\right)$
11. $\quad y=\cos \left(x-\frac{\pi}{3}\right)$
12. $\quad y=\sin \left(x+\frac{\pi}{3}\right)$
13. $\quad y=\sin \left(x-\frac{3 \pi}{4}\right) \quad$

14. $\quad y=\cos \left(x+\frac{3 \pi}{4}\right)$
15. $\quad y=\cos \left(x+\frac{2 \pi}{3}\right) \quad$

16. $\quad y=\sin \left(x-\frac{2 \pi}{3}\right)$