4.E: Funciones Exponenciales y Logarítmicas (Ejercicios)
- Page ID
- 121443
4.1: Funciones exponenciales
Cuando las poblaciones crecen rápidamente, a menudo decimos que el crecimiento es “exponencial”, lo que significa que algo está creciendo muy rápidamente. Para un matemático, sin embargo, el término crecimiento exponencial tiene un significado muy específico. En esta sección, echaremos un vistazo a las funciones exponenciales, que modelan este tipo de rápido crecimiento.
Verbal
1) Explicar por qué los valores de una función exponencial creciente eventualmente superarán a los valores de una función lineal creciente.
- Respuesta:
-
Las funciones lineales tienen una tasa de cambio constante. Las funciones exponenciales aumentan con base en un porcentaje del original.
2) Dada una fórmula para una función exponencial, ¿es posible determinar si la función crece o decae exponencialmente con solo mirar la fórmula? Explique.
3) El Oxford Dictionary define la palabra nominal como un valor que es “declarado o expresado pero que no necesariamente corresponde exactamente al valor real”. Desarrollar un argumento razonable sobre por qué se utiliza el término tasa nominal para describir la tasa porcentual anual de una cuenta de inversión que compone el interés.
- Respuesta:
-
Cuando se agrava el interés, el porcentaje de intereses devengados al principal termina siendo mayor que la tasa porcentual anual para la cuenta de inversión. Así, la tasa porcentual anual no corresponde necesariamente a los intereses reales devengados, que es la definición misma de nominal.
Algebraico
Para los siguientes ejercicios, identifique si la declaración representa una función exponencial. Explique.
4) El incremento promedio anual de la población de una manada de lobos es\(25\).
5) Una población de bacterias disminuye por un factor de\(\frac{1}{8}\) cada\(24\) hora.
- Respuesta:
-
exponencial; la población disminuye por una tasa proporcional.
6) El valor de una colección de monedas ha aumentado en\(3.25\%\)
7) Por cada sesión de entrenamiento, un entrenador personal cobra a sus clientes\(\$5\) menos que la sesión de entrenamiento anterior.
- Respuesta:
-
no exponencial; la carga disminuye en una cantidad constante cada visita, por lo que la sentencia representa una función lineal.
8) La altura de un proyectil en el momento\(t\) está representada por la función\(h(t)= -4.9t^2 + 18t + 40\)
Para los siguientes ejercicios, considere este escenario: Para cada año \(t\), la población de un bosque de árboles está representada por la función \(A(t)=115(1.025)^t\).
9) ¿Qué población forestal crece a un ritmo más rápido?
- Respuesta:
-
El bosque representado por la función\(B(t)=82(1.029)^t\).
10) ¿Qué bosque tuvo un mayor número de árboles inicialmente? ¿Por cuántos?
11) Suponiendo que los modelos de crecimiento poblacional sigan representando el crecimiento de los bosques, ¿qué bosque tendrá un mayor número de árboles después de\(20\) años? ¿Por cuántos?
- Respuesta:
-
Después de\(t=20\) años, el bosque A tendrá\(43\)
12) Suponiendo que los modelos de crecimiento poblacional sigan representando el crecimiento de los bosques, cuyos bosques tendrán un mayor número de árboles después\(100\)
13) Discutir los resultados anteriores de los cuatro ejercicios anteriores. Suponiendo que los modelos de crecimiento poblacional sigan representando el crecimiento de los bosques, ¿qué bosque tendrá el mayor número de árboles a largo plazo? ¿Por qué? ¿Cuáles son algunos factores que podrían influir en la validez a largo plazo del modelo de crecimiento exponencial?
- Respuesta:
-
Las respuestas variarán. Respuesta muestral: Durante varios años, la población del bosque A superará cada vez más al bosque B, pero debido a que el bosque B en realidad crece a un ritmo más rápido, la población eventualmente llegará a ser más grande que el bosque A y seguirá siendo así mientras se mantengan los modelos de crecimiento poblacional. Algunos factores que podrían influir en la validez a largo plazo del modelo de crecimiento exponencial son la sequía, una epidemia que destruye a la población, y otros factores ambientales y biológicos.
Para los siguientes ejercicios, determine si la ecuación representa crecimiento exponencial, decaimiento exponencial, o ninguno. Explique.
14)\(y=300(1−t)^5\)
15)\(y=220(1.06)^x\)
- Respuesta:
-
crecimiento exponencial; El factor de crecimiento,\(1.06\) es mayor que\(1\).
16)\(y=16.5(1.025)^{\frac{1}{x}}\)
17)\(y=11,701(0.97)^t\)
- Respuesta:
-
decaimiento exponencial; El factor de decaimiento,\(0.97\)
, .
Para los siguientes ejercicios, encuentra la fórmula para una función exponencial que pase por los dos puntos dados.
18) (\(0,6)\)y\((3,750)\)
19)\((0,2000)\)
- Respuesta:
-
\(f(x)=2000(0.1)^x\)
20)\(\left (−1,\frac{3}{2} \right )\) y\((3,24)\)
21)\((−2,6)\)
- Respuesta:
-
\(f(x)=\left ( \frac{1}{6} \right )^{-\frac{3}{5}} \left ( \frac{1}{6} \right )^{\frac{x}{5}}\approx 2.93 (0.699)^x\)
22)\((3,1)\) y\((5,4)\)
Para los siguientes ejercicios, determine si la tabla podría representar una función lineal, exponencial o ninguna. Si parece ser exponencial, encuentra una función que pase por los puntos.
23)
| \(x\) | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| \(f(x)\) | 70 | 40 | 10 | -20 |
- Respuesta:
-
Lineal
24)
| \(x\) | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| \(h(x)\) | 70 | 49 | 34.3 | 24.01 |
25)
| \(x\) | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| \(m(x)\) | 80 | 61 | 42.9 | 25.61 |
- Respuesta:
-
Tampoco
26)
| \(x\) | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| \(f(x)\) | 10 | 20 | 40 | 80 |
27)
| \(x\) | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| \(g(x)\) | -3.25 | 2 | 7.25 | 12.5 |
- Respuesta:
-
Lineal
Para los siguientes ejercicios, utilice la fórmula de interés compuesto,\(A(t)=P\left (1+ \frac{r}{n} \right )^{nt}\)
28) Después de cierto número de años, el valor de una cuenta de inversión está representado por la ecuación\(10,250\left (1+ \frac{0.04}{12} \right )^{120}\)
29) ¿Cuál fue el depósito inicial realizado en la cuenta en el ejercicio anterior?
- Respuesta:
-
\(\$10,250\)
30) ¿Cuántos años había ido acumulando intereses la cuenta del ejercicio anterior?
31) Se abre una cuenta con un depósito inicial de\(\$6,500\) y gana\(3.6\%\) intereses compuestos semestralmente. ¿Cuál será el valor de la cuenta en\(20\) años?
- Respuesta:
-
\(\$13,268.58\)
32) ¿Cuánto más habría valido la cuenta en el ejercicio anterior si los intereses se estuvieran componiendo semanalmente?
33) Resolver la fórmula de interés compuesto para el principal,\(P\).
- Respuesta:
-
\(P=A(t)\cdot \left (1+ \frac{r}{n} \right )^{-nt}\)
34) Utilizar la fórmula encontrada en el ejercicio anterior para calcular el depósito inicial de una cuenta que vale\(\$14,472.74\) después de ganar\(5.5\%\)
35) ¿Cuánto más valdría la cuenta en los dos ejercicios anteriores si estuviera ganando intereses por\(5\) más años?
- Respuesta:
-
\(\$4,572.56\)
36) Utilizar propiedades de exponentes racionales para resolver la fórmula de interés compuesto para la tasa de interés,\(r\).
37) Utilizar la fórmula encontrada en el ejercicio anterior para calcular la tasa de interés de una cuenta que se compuso semestralmente, tenía un depósito inicial de\(\$9,000\) y valía\(\$13,373.53\) después de\(10\) años.
- Respuesta:
-
\(4\%\)
38) Utilizar la fórmula encontrada en el ejercicio anterior para calcular la tasa de interés de una cuenta que se compuso mensualmente, tenía un depósito inicial de\(\$5,500\), y valía\(\$38,455\) después de\(30\) años.
Para los siguientes ejercicios, determine si la ecuación representa crecimiento continuo, decaimiento continuo, o ninguno. Explique.
39)\(y=3742(e)^{0.75t}\)
- Respuesta:
-
crecimiento continuo; la tasa de crecimiento es mayor que\(0\).
40)\(y=150(e)^{\frac{3.25}{t}}\)
41)\(y=2.25(e)^{-2t}\)
- Respuesta:
-
decaimiento continuo; la tasa de crecimiento es menor que\(0\).
42) Supongamos que se abre una cuenta de inversión con un depósito inicial de\(\$12,000\) ganancias\(7.2\%\)
43) ¿Cuánto menos valdría la cuenta del Ejercicio 42 después de\(30\) años si en su lugar fuera compuesta mensualmente?
- Respuesta:
-
\(\$669.42\)
Numérico
Para los siguientes ejercicios, evalúe cada función. Redondear las respuestas a cuatro decimales, si es necesario.
44)\(f(x)=2(5)^x\) para\(f(-3)\)
45)\(f(x)=-4^{2x+3}\) para\(f(-1)\)
- Respuesta:
-
\(f(-1)=-4\)
46)\(f(x)=e^x\), para\(f(3)\)
47)\(f(x)=-2e^{x-1}\), para\(f(-1)\)
- Respuesta:
-
\(f(-1)\approx -0.2707\)
48)\(f(x)=2.7(4)^{-x+1}+1.5\), para\(f(-2)\)
49)\(f(x)=1.2e^{2x}-0.3\), para\(f(3)\)
- Respuesta:
-
\(f(3)\approx 483.8146\)
50)\(f(x)=-\frac{3}{2}(3)^{-x}+\frac{3}{2}\), para\(f(2)\)
Tecnología
Para los siguientes ejercicios, utilice una calculadora gráfica para encontrar la ecuación de una función exponencial dados los puntos en la curva.
51)\((0,3)\) y\((3,375)\)
- Respuesta:
-
\(y=3\cdot 5^x\)
52)\((3,222.62)\) y\((10,77.456)\)
53)\((20,29.495)\) y\((150,730.89)\)
- Respuesta:
-
\(y\approx 18\cdot 1.025^x\)
54)\((5,2.909)\) y\((13,0.005)\)
55) ((11,310.035)\) y\((25,356.3652)\)
- Respuesta:
-
\(y\approx 0.2\cdot 1.95^x\)
Extensiones
56) El rendimiento porcentual anual (APY) de una cuenta de inversión es una representación de la tasa de interés real ganada en una cuenta compuesta. Se basa en un periodo compuesto de un año. Demostrar que el APY de una cuenta que compuestos mensualmente se puede encontrar con la fórmula\(APY=\left (1+\frac{r}{12} \right )^{12}-1\)
57) Repetir el ejercicio anterior para encontrar la fórmula para el APY de una cuenta que se componga diariamente. Utilizar los resultados de éste y del ejercicio anterior para desarrollar una función\(I(n)\)
- Respuesta:
-
\(\begin{align*} APY &= \frac{A(t)-a}{a}\\ &= \frac{a\left ( 1+\frac{r}{365} \right )^{365(1)}-a}{a}\\ &= \frac{a\left [\left ( 1+\frac{r}{365} \right )^{365}-1 \right ]}{a}\\ &= \left ( 1+\frac{r}{365} \right )^{365}-1 \end{align*}\);\(I(n)=\left ( 1+\frac{r}{n} \right )^n - 1\)
58) Recordemos que una función exponencial es cualquier ecuación escrita en la forma\(f(x)=a\cdot b^x\) tal que\(a\) y\(b\) son números positivos y\(b≠1\). Cualquier número positivo\(b\)
59) En una función de decaimiento exponencial, la base del exponente es un valor entre\(0\) y\(1\). Así, para algún número\(b>1\),
- Respuesta:
-
\(f\)Sea la función de decaimiento exponencial\(f(x)=a\cdot \left (\frac{1}{b} \right )^x\) tal que\(b>1\). Entonces para algún número\(n>0\),
\(\begin{align*} f(x) &= a\cdot \left (\frac{1}{b} \right )^x \\ &= a \left (b^{-1} \right )^x\\ &= a\left ( (e^n)^{-1} \right )^x\\ &= a\left ( e^{-n} \right )^x\\ &= a(e)^{-nx} \end{align*}\)
60) La fórmula para el monto\(A\) en una cuenta de inversión con una tasa de interés nominal\(r\) en cualquier momento\(t\) viene dada por\(A(t)=a(e)^{rt}\), donde\(a\)
Aplicaciones del mundo real
61) La población de zorros en una determinada región tiene una tasa de crecimiento\(9\%\) anual anual. En el año 2012, se contabilizaron\(23,900\) zorros en la zona. ¿Cuál es la población de zorros pronosticada para ser en el año 2020?
- Respuesta:
-
\(47,622\)zorro
62) Un científico comienza con\(100\) miligramos de una sustancia radiactiva que se descompone exponencialmente. Después de\(35\) horas, quedan\(50\) mg de la sustancia. ¿Cuántos miligramos quedarán después de\(54\) horas?
63) En el año 1985, se valoró una casa en\(\$110,000\). Para el año 2005, el valor se había apreciado\(\$145,000\). ¿Cuál fue la tasa de crecimiento anual entre 1985 y 2005? Supongamos que el valor siguió creciendo en el mismo porcentaje. ¿Cuál era el valor de la casa en el año 2010?
- Respuesta:
-
\(1.39\%\);\(\$155,368.09\)
64) Un automóvil fue valorado\(\$38,000\) en el año 2007. Para 2013, el valor se había depreciado a\(\$11,000\) Si el valor del automóvil sigue bajando en el mismo porcentaje, ¿cuánto valdrá para 2017?
65) Jamal quiere ahorrar\(\$54,000\) para el pago inicial de una vivienda. ¿Cuánto necesitará invertir en una cuenta con\(8.2\%\) APR, componiendo diariamente, para poder alcanzar su meta en\(5\) años?
- Respuesta:
-
\(\$35,838.76\)
66) Kyoko tiene\(\$10,000\) que quiere invertir. Su banco tiene varias cuentas de inversión para elegir, todas compuestas diariamente. Su objetivo es tener\(\$15,000\) para cuando termine la escuela de posgrado en\(6\) años. A la centésima de porcentaje más cercana, ¿cuál debería ser su tasa mínima de interés anual para alcanzar su meta? (Pista: resolver la fórmula de interés compuesto para la tasa de interés.)
67) Alyssa abrió una cuenta de retiro con\(7.25\%\) APR en el año 2000. Su depósito inicial fue\(\$13,500\). ¿Cuánto valdrá la cuenta en 2025 si los intereses se agravan mensualmente? ¿Cuánto más ganaría si el interés se agravara continuamente?
- Respuesta:
-
\(\$82,247.78\);\(\$449.75\)
68)\(7\%\) Se abrió una cuenta de inversión con una tasa de interés anual de con un depósito inicial de\(\$4,000\) Comparar los valores de la cuenta después de\(9\) años en que el interés se compone anual, trimestral, mensual y continuamente.
4.2: Gráficas de Funciones Exponenciales
Como discutimos en la sección anterior, las funciones exponenciales se utilizan para muchas aplicaciones del mundo real como finanzas, forense, ciencias de la computación y la mayoría de las ciencias de la vida. Trabajar con una ecuación que describa una situación del mundo real nos da un método para hacer predicciones. La mayoría de las veces, sin embargo, la ecuación en sí no es suficiente. Aprendemos mucho de las cosas al ver sus representaciones pictóricas, y es exactamente por eso que graficar ecuaciones exponenciales es una herramienta poderosa.
Verbal
1) ¿Qué papel juega la asíntota horizontal de una función exponencial al decirnos sobre el comportamiento final de la gráfica?
- Respuesta:
-
Una asíntota es una línea a la que se acerca la gráfica de una función,\(x\) ya que aumenta o disminuye sin límite. La asíntota horizontal de una función exponencial nos dice el límite de los valores de la función ya que la variable independiente se vuelve extremadamente grande o extremadamente pequeña.
2) ¿Cuál es la ventaja de saber reconocer las transformaciones de la gráfica de una función padre algebraicamente?
Algebraico
3) La gráfica de\(f(x) = 3^x\)
- Respuesta:
-
\(g(x)=4(3)^{-x}\)
; intercepción en Y: ;
4) La gráfica de\(f(x)=\left ( \frac{1}{2} \right )^{-x}\)
5) La gráfica de\(f(x)=10^x\) se refleja alrededor del\(x\) eje -y\(7\) unidades desplazadas hacia arriba. ¿Cuál es la ecuación de la nueva función,\(g(x)\)?
- Respuesta:
-
\(g(x)=-10^x + 7\);\(y\) -interceptar:\((0,6)\); Dominio: todos los números reales; Rango: todos los números reales menores que\(7\).
6) La gráfica de\(3\) unidades\(f(x)=(1.68)^x\) se desplaza a la derecha, estirada verticalmente por un factor de\(2\)
7) La gráfica de\(2\) unidades\(f(x)=2\left ( \frac{1}{4} \right )^{x-20}\) es desplazada a la izquierda, estirada verticalmente por un factor de\(4\)
- Respuesta:
-
\(g(x)=2\left ( \frac{1}{4} \right )^x\);\(y\) -interceptar:\((0,2)\);
Gráfica
Para los siguientes ejercicios, graficar la función y su reflejo alrededor del\(y\) eje -en los mismos ejes, y dar la\(y\) -intercepción.
8)\(f(x)=3\left ( \frac{1}{2} \right )^x\)
9)\(g(x)=-2(0.25)^x\)
- Respuesta:
-
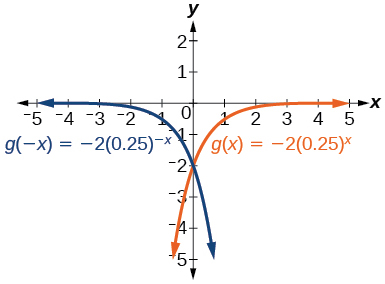
\(y\)-interceptar:\((0,-2)\)
10)\(h(x)=6(1.75)^{-x}\)
Para los siguientes ejercicios, grafica cada conjunto de funciones en los mismos ejes.
11)\(f(x)=3\left ( \frac{1}{4} \right )^x, g(x)=3(2)^x, h(x)=3(4)^x\)
- Respuesta:
-
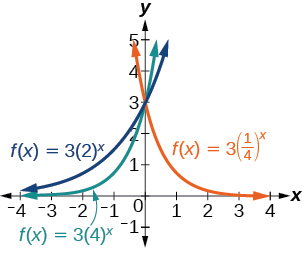
12)\(f(x)=\frac{1}{4}(3)^x, g(x)=2(3)^x, h(x)=4(3)^x\)
Para los siguientes ejercicios, haga coincidir cada función con una de las gráficas de la Figura a continuación.
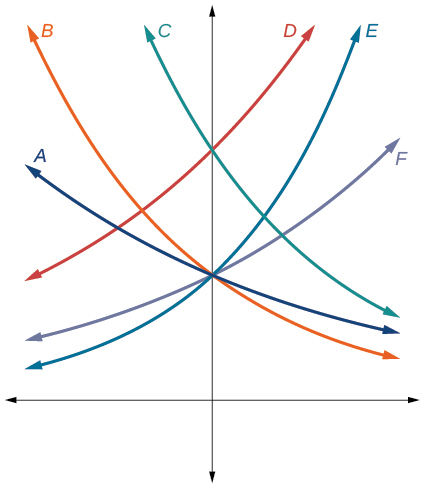
13)\(f(x)=2(0.69)^x\)
- Respuesta:
-
B
14)\(f(x)=2(1.28)^x\)
15)\(f(x)=2(0.81)^x\)
- Respuesta:
-
A
16)\(f(x)=4(1.28)^x\)
17)\(f(x)=2(1.59)^x\)
- Respuesta:
-
E
18)\(f(x)=4(0.69)^x\)
Para los siguientes ejercicios, utilice las gráficas que se muestran en la Figura a continuación. Todos tienen la forma\(f(x)=ab^x\).
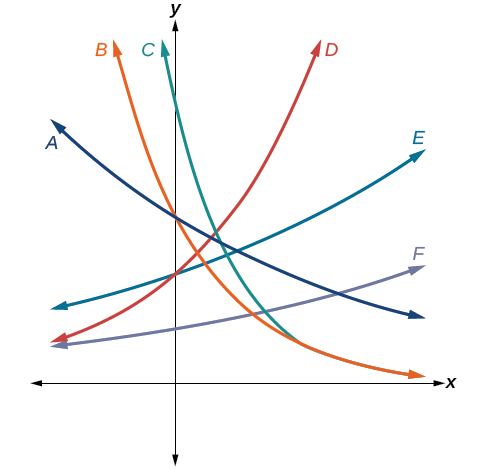
19) ¿Para qué gráfica tiene el mayor valor\(b\)?
- Respuesta:
-
D
20) ¿Para qué gráfica tiene el menor valor\(b\)?
21) ¿Para qué gráfica tiene el mayor valor\(a\)?
- Respuesta:
-
C
22) ¿Para qué gráfica tiene el menor valor\(a\)?
Para los siguientes ejercicios, grafica la función y su reflejo alrededor del\(x\) eje -en los mismos ejes.
23)\(f(x)=\frac{1}{2}(4)^x\)
- Respuesta:
-
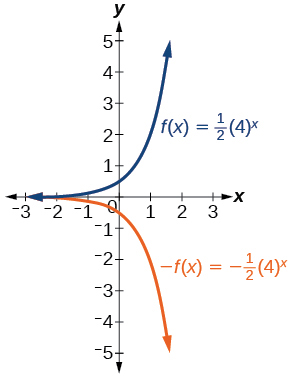
24)\(f(x)=3(0.75)^x-1\)
25)\(f(x)=-4(2)^x+2\)
- Respuesta:
-
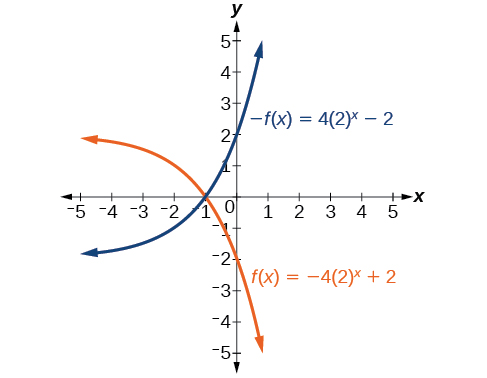
Para los siguientes ejercicios, grafica la transformación de\(f(x)=2^x\)
26)\(f(x)=2^{-x}\)
27)\(h(x)=2^x+3\)
- Respuesta:
-
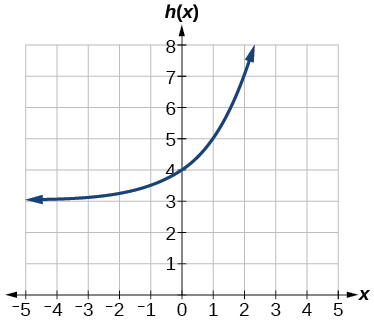
Asintota horizontal:\(h(x)=3\)
;
28)\(f(x)=2^{x-2}\)
Para los siguientes ejercicios, describa el comportamiento final de las gráficas de las funciones.
29)\(f(x)=-5(4)^x-1\)
- Respuesta:
-
Como\(x\rightarrow \infty , f(x)\rightarrow -\infty\)
Como\(x\rightarrow -\infty , f(x)\rightarrow -1\)
30)\(f(x)=3\left ( \frac{1}{2} \right )^x-2\)
31)\(f(x)=3(4)^{-x}+2\)
- Respuesta:
-
Como\(x\rightarrow \infty , f(x)\rightarrow 2\)
Como\(x\rightarrow -\infty , f(x)\rightarrow \infty\)
Para los siguientes ejercicios, comience con la gráfica de\(f(x)=4^x\)
32)\(f(x)\)\(4\) Unidades de cambio hacia arriba
33) Desplazamiento\(f(x)\) \(3\) units hacia abajo
- Respuesta:
-
\(f(x)=4^x-3\)
34)\(f(x)\)\(2\) Unidades de cambio a la izquierda
35)\(f(x)\)\(5\) Unidades de cambio a la derecha
- Respuesta:
-
\(f(x)=4^{x-5}\)
36) Reflexionar\(f(x)\) sobre el\(x\) eje
37) Reflexionar\(f(x)\) sobre el\(y\) eje
- Respuesta:
-
\(f(x)=4^{-x}\)
Para los siguientes ejercicios, cada gráfica es una transformación de\(f(x)=2^x\)
38)
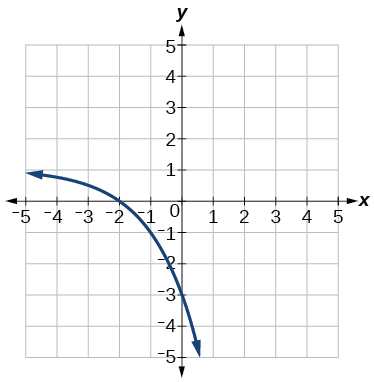
39)
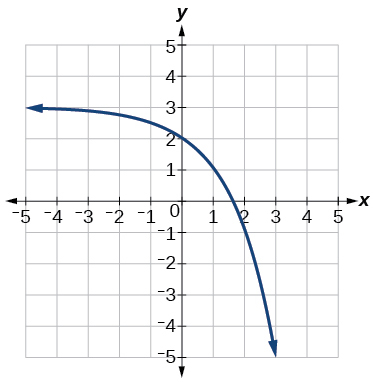
- Respuesta:
-
\(y=-2^x+3\)
40)
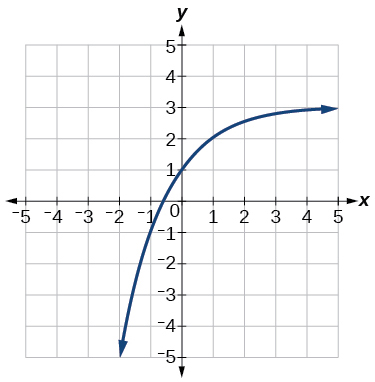
Para los siguientes ejercicios, encuentra una ecuación exponencial para la gráfica.
41)
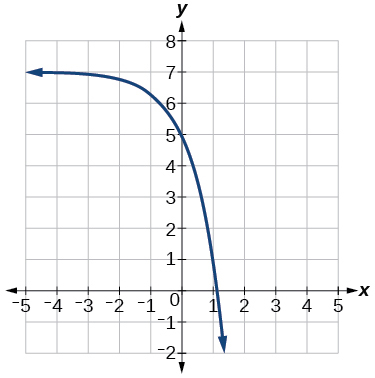
- Respuesta:
-
\(y=-2(3)^x+7\)
42)
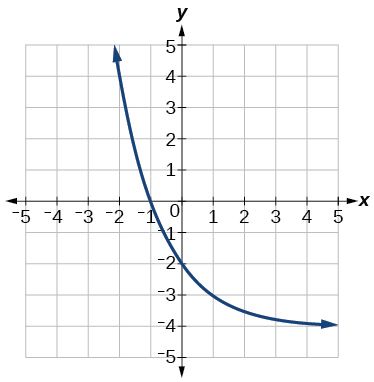
Numérico
Para los siguientes ejercicios, evaluar las funciones exponenciales para el valor indicado de\(x\).
43)\(g(x)=\frac{1}{3}(7)^{x-2}\) para\(g(6)\).
- Respuesta:
-
\(g(6)=800+\frac{1}{3}\approx 800.3333\)
44)\(f(x)=4(2)^{x-1}-2\) para\(f(5)\).
45)\(h(x)=-\frac{1}{2}\left ( \frac{1}{2} \right )^x+6\) para\(h(-7)\).
- Respuesta:
-
\(h(-7)=-58\)
Tecnología
Para los siguientes ejercicios, utilice una calculadora gráfica para aproximar las soluciones de la ecuación. Redondear a la milésima más cercana.
46)\(-50=\left ( \frac{1}{2} \right )^{-x}\)
47)\(116=\left ( \frac{1}{4} \right )\left ( \frac{1}{8} \right )^x\)
- Respuesta:
-
\(x\approx -2.953\)
48)\(12=2(3)^x+1\)
49)\(5=3\left ( \frac{1}{2} \right )^{x-1}-2\)
- Respuesta:
-
\(x\approx -0.222\)
50)\(-30=-4(2)^{x+2}+2\)
Extensiones
51) Explorar y discutir las gráficas de\(F(x)=(b)^x\) y\(G(x)=\left ( \frac{1}{b} \right )^x\). Después hacer una conjetura sobre la relación entre las gráficas de las funciones\(b^x\) y\(\left ( \frac{1}{b} \right )^x\) para cualquier número real\(b>0\).
- Respuesta:
-
La gráfica de\(G(x)=\left ( \frac{1}{b} \right )^x\) es la refelción sobre el\(y\) -eje de la gráfica de\(F(x)=(b)^x\); Para cualquier número real\(b>0\) y función\(f(x)=(b)^x\)
,
52) Demostrar la conjetura hecha en el ejercicio anterior.
53) Explorar y discutir las gráficas de\(f(x) = 4^x\),\(g(x)=4^{x-2}\), y\(h(x)=\left ( \frac{1}{16} \right )4^x\)
- Respuesta:
-
Las gráficas de\(g(x)\) y\(h(x)\) son las mismas y son un desplazamiento horizontal a la derecha de la gráfica de\(f(x)\); Para cualquier número real\(n\)\(b>0\), número real y función\(f(x)=b^x\)
,
54) Demostrar la conjetura hecha en el ejercicio anterior.
4.3: Funciones logarítmicas
La inversa de una función exponencial es una función logarítmica, y la inversa de una función logarítmica es una función exponencial.
Verbal
1) ¿Qué es un\(b\) logaritmo base? Discutir el significado interpretando cada parte de las ecuaciones equivalentes\(b^y=x\) y\(\log _bx=y\) para\(b>0, b\neq 1\).
- Contestar
-
Un logaritmo es un exponente. Específicamente, es el exponente al que\(b\) se eleva una base para producir un valor dado. En las expresiones dadas, la base\(b\) tiene el mismo valor. El exponente,\(y\)
, ,
2) ¿Cómo se\(f(x)=\log _bx\) relaciona la función logarítmica con la función exponencial\(g(x)=b^x\)? ¿Cuál es el resultado de componer estas dos funciones?
3) ¿Cómo se\(\log _bx=y\) puede resolver la ecuación logarítmica para\(x\) usar las propiedades de los exponentes?
- Contestar
-
Dado que la ecuación de un logaritmo es equivalente a una ecuación exponencial, el logaritmo se puede convertir a la ecuación exponencial\(b^y = x\)
, .
4) Discutir el significado del logaritmo común. Cuál es su relación con un logaritmo con base\(b\)
5) Discutir el significado del logaritmo natural. Cuál es su relación con un logaritmo con base\(b\)
- Contestar
-
El logaritmo natural es un caso especial del logaritmo con base\(b\) en que el logaritmo natural siempre tiene base\(e\).
, .
Algebraico
Para los siguientes ejercicios, reescribe cada ecuación en forma exponencial.
6)\(\log_{4}(q)=m\)
7)\(\log_{a}(b)=c\)
- Contestar
-
\(a^c=b\)
8)\(\log_{16}(y)=x\)
9)\(\log_{x}(64)=y\)
- Contestar
-
\(x^y=64\)
10)\(\log_{y}(x)=-11\)
11)\(\log_{15}(a)=b\)
- Contestar
-
\(15^b=a\)
12)\(\log_{y}(137)=x\)
13)\(\log_{13}(142)=a\)
- Contestar
-
\(13^a=142\)
14)\(\log(v)=t\)
15)\(\ln(w)=n\)
- Contestar
-
\(e^n=w\)
Para los siguientes ejercicios, reescribe cada ecuación en forma logarítmica.
16)\(4^x=y\)
17)\(c^d=k\)
- Contestar
-
\(\log_{c}(k)=d\)
18)\(m^{-7}=n\)
19)\(19^x=y\)
- Contestar
-
\(\log_{19}(y)=x\)
20)\(x^{-\frac{10}{13}}=y\)
21)\(n^4 = 103\)
- Contestar
-
\(\log_{n}(103)=4\)
22)\(\left ( \dfrac{7}{5} \right )^m=n\)
23)\(y^x=\dfrac{39}{100}\)
- Contestar
-
\(\log_{y}\left ( \dfrac{39}{100} \right )=x\)
24)\(10^a=b\)
25)\(e^k=h\)
- Contestar
-
\(\ln(w)=n\)
Para los siguientes ejercicios, resuelva para\(x\) convirtiendo la ecuación logarítmica a forma exponencial.
26)\(\log_{3}(x)=2\)
27)\(\log_{2}(x)=-3\)
- Contestar
-
\(x=2^{-3}=\dfrac{1}{8}\)
28)\(\log_{5}(x)=2\)
29)\(\log_{3}(x)=3\)
- Contestar
-
\(x = 3^3 = 27\)
30)\(\log_{2}(x)=6\)
31)\(\log_{9}(x)=\dfrac{1}{2}\)
- Contestar
-
\(x=9^{\frac{1}{2}}=3\)
32)\(\log_{18}(x)=2\)
33)\(\log_{6}(x)=-3\)
- Contestar
-
\(x=6^{-3}=\dfrac{1}{216}\)
34)\(\log (x)=3\)
35)\(\ln(x)=2\)
- Contestar
-
\(x=e^2\)
Para los siguientes ejercicios, utilice la definición de logaritmos comunes y naturales para simplificar.
36)\(\log (100^8)\)
37)\(10^{\log (32)}\)
- Contestar
-
\(32\)
38)\(2\log (.0001)\)
39)\(e^{\ln (1.06)}\)
- Contestar
-
\(1.06\)
40)\(\ln (e^{-5.03})\)
41)\(e^{\ln (10.125)}+4\)
- Contestar
-
\(14.125\)
Numérico
Para los siguientes ejercicios, evalúe la expresión\(b\) logarítmica base sin usar una calculadora.
42)\(\log _3\left ( \frac{1}{27} \right )\)
43)\(\log _6(\sqrt{6})\)
- Contestar
-
\(\dfrac{1}{2} \)
44)\(\log _2\left ( \frac{1}{8} \right )+4\)
45)\(6\log _8(4)\)
- Contestar
-
\(4\)
Para los siguientes ejercicios, evalúe la expresión logarítmica común sin usar una calculadora.
46)\(\log (10,000)\)
47)\(\log (0.001)\)
- Contestar
-
\(-3\)
48)\(\log (1)+7\)
49)\(2\log (100^{-3})\)
- Contestar
-
\(-12\)
Para los siguientes ejercicios, evalúe la expresión logarítmica natural sin usar una calculadora.
50)\(\ln \left ( e^{\frac{1}{3}} \right )\)
51)\(\ln (1)\)
- Contestar
-
\(0\)
52)\(\ln \left ( e^{-0.225} \right )-3\)
53)\(25\ln \left ( e^{\frac{2}{5}} \right )\)
- Contestar
-
\(10\)
Tecnología
Para los siguientes ejercicios, evalúe cada expresión usando una calculadora. Redondear a la milésima más cercana.
54)\(\log (0.04)\)
55)\(\ln (15)\)
- Contestar
-
\(2.708\)
56)\(\ln \left ( {\frac{4}{5}} \right )\)
57)\(\log (\sqrt{2})\)
- Contestar
-
\(0.151\)
58)\(\ln (\sqrt{2})\)
Extensiones
59) ¿Está\(x=0\) en el dominio de la función\(f(x)=\log x\)? Si es así, ¿cuál es el valor de la función cuándo\(x=0\)? Verificar el resultado.
- Contestar
-
No, la función no tiene valor definido para\(x=0\)
. . . ,
60) ¿Está\(f(x)=0\) en el rango de la función\(f(x)=\log (x)\)?
61) ¿Hay un número\(x\) tal que\(\ln x = 2\)? Si es así, ¿cuál es ese número? Verificar el resultado.
- Contestar
-
Sí. Supongamos que existe un número real\(x\) tal que\(\ln x = 2\)
. , . .
62) Es cierto lo siguiente:\(\frac{\log _3(27)}{\log _4\left ( \frac{1}{64} \right )}=-1\)
63) Es cierto lo siguiente:\(\frac{\ln (e^{1.725})}{\ln (1)}=1.725\) Verificar el resultado.
- Contestar
-
No;\(\ln (1) =0\), así\(\frac{\ln (e^{1.725})}{\ln (1)}=1.725\) es indefinido.
Aplicaciones del mundo real
64) El índice de exposición\(EI\) para una cámara\(35\) milimétrica es una medida de la cantidad de luz que golpea la película. Se determina por la ecuación\(EI=\log _2\left ( \frac{f^2}{t} \right )\)
65) Refiérase al ejercicio anterior. Supongamos que el medidor de luz en una cámara indica una\(EI\) de\(-2\)
- Contestar
-
\(2\)
66) Los niveles\(I\) de intensidad de dos sismos medidos en un sismógrafo se pueden comparar por la fórmula\(\log \left ( \frac{I_1}{I_2} \right )=M_1-M_2\)
4.4: Gráficas de funciones logarítmicas
En esta sección discutiremos los valores para los que se define una función logarítmica, y luego volveremos nuestra atención a graficar la familia de funciones logarítmicas.
Verbal
1) La inversa de cada función logarítmica es una función exponencial y viceversa. ¿Qué nos dice esto sobre la relación entre las coordenadas de los puntos en las gráficas de cada uno?
- Contestar
-
Dado que las funciones son inversas, sus gráficas son imágenes especular sobre la línea\(y-x\)
.
2) ¿Qué tipo (s) de traducción (es), en su caso, afectan al rango de una función logarítmica?
3) ¿Qué tipo (s) de traducción (es), en su caso, afectan al dominio de una función logarítmica?
- Contestar
-
Desplazar la función hacia la derecha o hacia la izquierda y reflejar la función alrededor\(y\) del eje -afectará su dominio.
4) Considerar la función logarítmica general\(f(x)=\log _b(x)\)
5) ¿La gráfica de una función logarítmica general tiene una asíntota horizontal? Explique.
- Contestar
-
No. Una asíntota horizontal sugeriría un límite en el rango, y el rango de cualquier función logarítmica en forma general es todos números reales.
Algebraico
Para los siguientes ejercicios, indique el dominio y rango de la función.
6)\(f(x)=\log _3(x+4)\)
7)\(h(x)=\ln \left ( \dfrac{1}{2}-x \right )\)
- Contestar
-
Dominio:\(\left ( -\infty , \dfrac{1}{2} \right )\); Rango:\((-\infty , \infty )\)
8)\(g(x)=\log _5(2x+9)-2\)
9)\(h(x)=\ln (4x+17)-5\)
- Contestar
-
Dominio:\(\left ( -\dfrac{17}{4}, \infty \right )\); Rango:\((-\infty , \infty )\)
10)\(f(x)=\log _2 (12-3x)-3\)
Para los siguientes ejercicios, indique el dominio y la asíntota vertical de la función.
11)\(f(x)=\log _b (x-5)\)
- Contestar
-
Dominio:\((5, \infty )\); asíntota vertical:\(x=5\)
12)\(g(x)=\ln (3-x)\)
13)\(f(x)=\log (3x+1)\)
- Contestar
-
Dominio:\(\left ( -\dfrac{1}{3}, \infty \right )\); asíntota vertical:\(x=-\dfrac{1}{3}\)
14)\(f(x)=3\log (-x)+2\)
15)\(g(x)=-\ln (3x+9)-7\)
- Contestar
-
Dominio:\((-3, \infty )\); asíntota vertical:\(x=-3\)
Para los siguientes ejercicios, indique el dominio, la asíntota vertical y el comportamiento final de la función.
16)\(f(x)=\ln (2-x)\)
17)\(f(x)=\log \left ( x-\dfrac{3}{7} \right )\)
- Contestar
-
Dominio:\(\left ( \dfrac{3}{7},\infty \right )\)
Asintota vertical:\(x=\dfrac{3}{7}\)
Comportamiento final: como\(x\rightarrow \left (\dfrac{3}{7} \right )^+\)\(f(x)\rightarrow -\infty\) y como\(x\rightarrow \infty ,f(x)\rightarrow \infty\)
18)\(h(x)=-\log (3x-4)+3\)
19)\(g(x)=\ln (2x+6)-5\)
- Contestar
-
Dominio:\(\left ( -3,\infty \right )\)
Asintota vertical:\(x=-3\)
Comportamiento final: como\(x\rightarrow -3^+\)\(f(x)\rightarrow -\infty\) y como\(x\rightarrow \infty ,f(x)\rightarrow \infty\)
20)\(f(x)=\log_3 (15-5x)+6\)
Para los siguientes ejercicios, indique el dominio, el rango y las intercepciones x e y, si existen. Si no existen, escriba DNE.
21)\(h(x)=\log_4 (x-1)+1\)
- Contestar
-
Dominio:\(\left (1,\infty \right )\)
Rango:\(-\infty , \infty \)
Asintota vertical:\(x=1\)
\(x\)-interceptar:\(\left ( \dfrac{5}{4},0\right )\)
\(y\)-intercepción: DNE
22)\(f(x)=\log (5x+10)+3\)
23)\(g(x)=\ln (-x)-2\)
- Contestar
-
Dominio:\(\left (-\infty ,0 \right )\)
Rango:\(-\infty , \infty \)
Asintota vertical:\(x=0\)
\(x\)-interceptar:\(\left ( -e^2,0 \right )\)
\(y\)-intercepción: DNE
24)\(f(x)=\log_2 (x+2)-5\)
25)\(h(x)=3\ln (x)-9\)
- Contestar
-
Dominio:\(\left (0,\infty \right )\)
Rango:\(-\infty , \infty \)
Asintota vertical:\(x=0\)
\(x\)-interceptar:\(\left ( e^3,0 \right )\)
\(y\)-intercepción: DNE
Gráfica
Para los siguientes ejercicios, haga coincidir cada función de la Figura siguiente con la letra correspondiente a su gráfica.
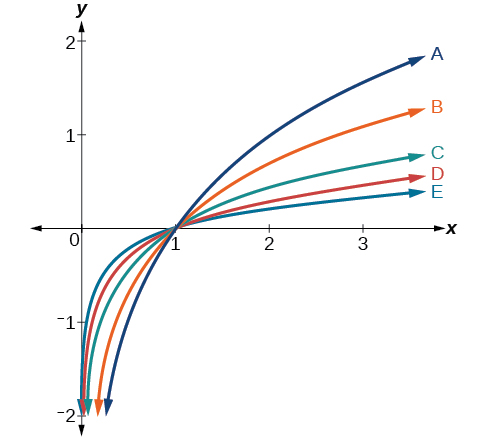
26)\(d(x)=\log (x)\)
27)\(f(x)=\ln (x)\)
- Contestar
-
\(B\)
28)\(g(x)=\log_2 (x)\)
29)\(h(x)=\log_5 (x)\)
- Contestar
-
\(C\)
30)\(j(x)=\log_{25} (x)\)
Para los siguientes ejercicios, haga coincidir cada función de la Figura con la letra correspondiente a su gráfica.
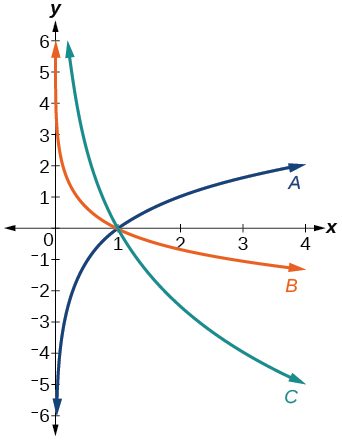
31)\(f(x)=\log_{\frac{1}{3}} (x)\)
- Contestar
-
\(B\)
32)\(g(x)=\log_2 (x)\)
33)\(h(x)=\log_{\frac{3}{4}} (x)\)
- Contestar
-
\(C\)
Para los siguientes ejercicios, esboce las gráficas de cada par de funciones en un mismo eje.
34)\(f(x)=\log (x)\) y\(g(x)=10^x\)
35)\(f(x)=e^x\) y\(g(x)=\ln (x)\)
- Contestar
-
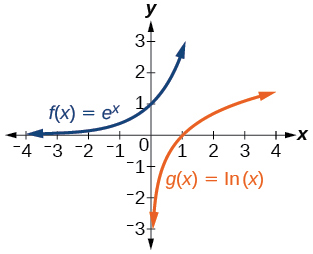
Para los siguientes ejercicios, haga coincidir cada función de la Figura con la letra correspondiente a su gráfica.
36)\(f(x)=\log _4(-x+2)\)
37)\(g(x)=-\log _4(x+2)\)
- Contestar
-
\(C\)
38)\(h(x)=\log _4(x+2)\)
Para los siguientes ejercicios, esboce la gráfica de la función indicada.
39)\(f(x)=\log _2(x+2)\)
- Contestar
-
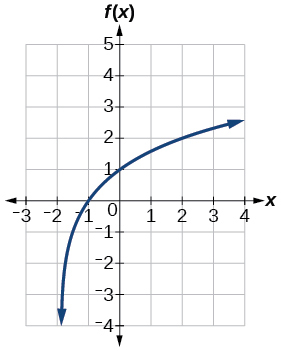
40)\(f(x)=2\log (x)\)
41)\(f(x)=\ln (-x)\)
- Contestar
-
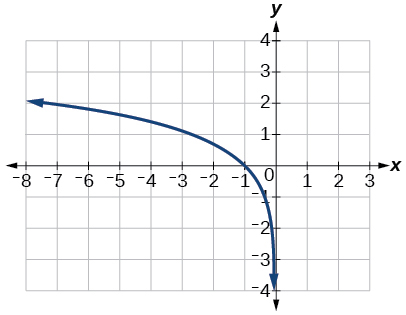
42)\(g(x)=\log (4x+16)+4\)
43)\(g(x)=\log (6-3x)+1\)
- Contestar
-
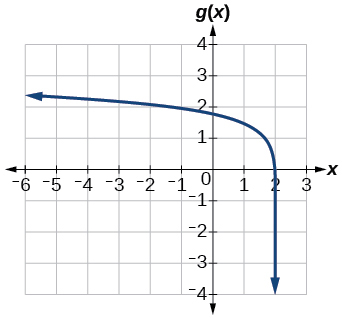
44)\(h(x)=-\dfrac{1}{2}\log (x+1)-3\)
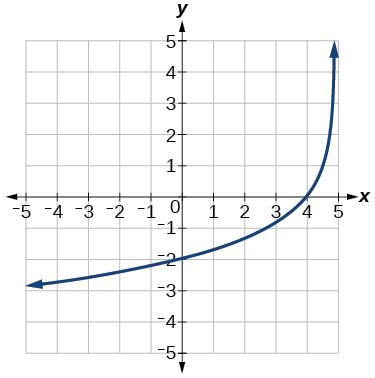
Para los siguientes ejercicios, escriba una ecuación logarítmica correspondiente a la gráfica mostrada.
45) Uso\(y=\log _2(x)\)

- Responder
-
\(f(x)=\log _2(-(x-1))\)
46) Utilizar\(f(x)=\log _3(x)\) como función padre.
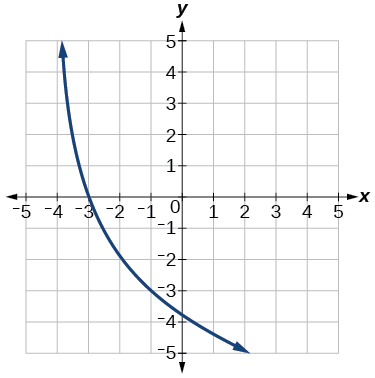
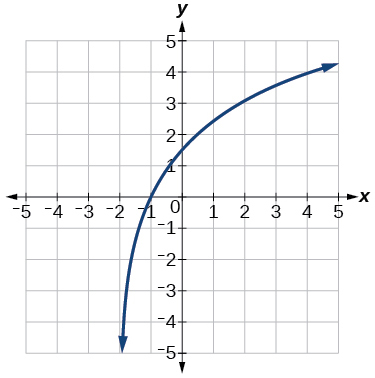
47) Utilizar\(f(x)=\log _4(x)\) como función padre.
- Responder
-
\(f(x)=3\log _4(x+2)\)
48) Utilizar\(f(x)=\log _5(x)\) como función padre.
Tecnología
Para los siguientes ejercicios, utilice una calculadora gráfica para encontrar soluciones aproximadas a cada ecuación.
49)\(\log (x-1)+2=\ln (x-1)+2\)
- Responder
-
\(x=2\)
50)\(\log (2x-3)+2=-\log (2x-3)+5\)
51)\(\ln (x-2)+2=-\ln (x+1)\)
- Responder
-
\(x\approx 2.303\)
52)\(2\ln (5x+1)=\dfrac{1}{2}\ln (-5x)+1\)
53)\(\dfrac{1}{3}\log (1-x)=\log (x+1)+\dfrac{1}{3}\)
- Responder
-
\(x\approx -0.472\)
Extensiones
54)\(b\) Sea cualquier número real positivo tal que\(b\neq 1\)
55) Explorar y discutir las gráficas de\(f(x)=\log_{\frac{1}{2}}(x)\) y\(g(x)=-\log _2(x)\)
- Responder
-
Las gráficas de\(f(x)=\log_{\frac{1}{2}}(x)\) y\(g(x)=-\log _2(x)\) parecen ser las mismas;
Conjetura: para cualquier base positiva\(b\neq 1\),\(\log_{b}(x)=\log_{\frac{1}{b}}(x)\)
56) Demostrar la conjetura hecha en el ejercicio anterior.
57) Cuál es el dominio de la función\(f(x)=\ln \left (\frac{x+2}{x-4} \right )\)
- Responder
-
Recordemos que el argumento de una función logarítmica debe ser positivo, por lo que determinamos dónde\(\frac{x+2}{x-4}> 0\). De la gráfica de la función\(f(x)=\frac{x+2}{x-4}\)
, . . 
58) Utilizar propiedades de exponentes para encontrar las\(x\) -intercepciones de la función\(f(x)=\log \left ( x^2+4x+4 \right )\) algebraicamente. Muestre los pasos para resolver y luego verifique el resultado graficando la función.
4.5: Propiedades logarítmicas
Recordemos que las funciones logarítmicas y exponenciales se “deshacen” entre sí. Esto significa que los logaritmos tienen propiedades similares a los exponentes. Aquí se dan algunas propiedades importantes de logaritmos.
Verbal
1) Cómo ayuda la regla de poder para logaritmos a la hora de resolver logaritmos con la forma\(\log _b(\sqrt[n]{x})\)
- Responder
-
Cualquier expresión raíz se puede reescribir como una expresión con un exponente racional para que se pueda aplicar la regla de potencia, haciendo que el logaritmo sea más fácil de calcular. Así,\(\log _b \left ( x^{\frac{1}{n}} \right ) = \dfrac{1}{n}\log_{b}(x)\).
2) ¿Qué hace la fórmula de cambio de base? ¿Por qué es útil cuando se usa una calculadora?
Algebraico
Para los siguientes ejercicios, expanda cada logaritmo tanto como sea posible. Reescriba cada expresión como suma, diferencia o producto de registros.
3)\(\log _b (7x\cdot 2y)\)
- Responder
-
\(\log _b (2)+\log _b (7)+\log _b (x)+\log _b (y)\)
4)\(\ln (3ab\cdot 5c)\)
5)\(\log_b \left ( \dfrac{13}{17} \right )\)
- Responder
-
\(\log _b (13)-\log _b (17)\)
6)\(\log_4 \left ( \dfrac{\frac{x}{z}}{w} \right )\)
7)\(\ln \left ( \dfrac{1}{4^k} \right )\)
- Responder
-
\(-k\ln(4)\)
8)\(\log _2 (y^x)\)
Para los siguientes ejercicios, condensar a un solo logaritmo si es posible.
9)\(\ln (7)+\ln (x)+\ln (y)\)
- Responder
-
\(\ln(7xy)\)
10)\(\log_3(2)+\log_3(a)+\log_3(11)+\log_3(b)\)
11)\(\log_b(28)-\log_b(7)\)
- Responder
-
\(\log_b(4)\)
12)\(\ln (a)-\ln (d)-\ln (c)\)
13)\(-\log_b\left ( \dfrac{1}{7} \right )\)
- Responder
-
\(\log_b(7)\)
14)\(\dfrac{1}{3}\ln(8)\)
Para los siguientes ejercicios, utilice las propiedades de logaritmos para expandir cada logaritmo tanto como sea posible. Reescriba cada expresión como suma, diferencia o producto de registros.
15)\(\log \left ( \dfrac{x^{15}y^{13}}{z^{19}} \right )\)
- Responder
-
\(15\log (x)+13\log (y)-19\log (z)\)
16)\(\ln \left ( \frac{a^{-2}}{b^{-4}c^{5}} \right )\)
17)\(\log \left ( \sqrt{x^3y^{-4}} \right )\)
- Responder
-
\(\frac{3}{2}\log (x)-2\log (y)\)
18)\(\ln \left ( y\sqrt{\frac{y}{1-y}} \right )\)
19)\(\log \left ( x^2y^3 \sqrt[3]{x^2y^5} \right )\)
- Responder
-
\(\dfrac{8}{3}\log (x)+\dfrac{14}{3}\log (y)\)
Para los siguientes ejercicios, condense cada expresión en un solo logaritmo utilizando las propiedades de logaritmos.
20)\(\log \left ( 2x^4 \right )+\log \left (3x^5 \right )\)
21)\(\ln \left ( 6x^9 \right )-\ln \left (3x^2 \right )\)
- Responder
-
\(\ln \left ( 2x^7 \right )\)
22)\(2\log (x)+3\log (x+1)\)
23)\(\log (x)-\dfrac{1}{2}\log (y)+3\log (z)\)
- Responder
-
\(\log \left ( \dfrac{xz^3}{\sqrt{y}} \right )\)
24)\(4\log _7(c)+\dfrac{\log _7(a)}{3}+\dfrac{\log _7(b)}{3}\)
Para los siguientes ejercicios, reescriba cada expresión como una proporción equivalente de registros utilizando la base indicada.
25)\(\log _7(15)\) a la base\(e\)
- Responder
-
\(\log _7(15)=\dfrac{\ln (15)}{\ln (7)}\)
Para los siguientes ejercicios, supongamos\(\log _5(6)=a\) y\(\log _5(11)=b\)
27)\(\log _{11} (5)\)
- Responder
-
\(\log _{11} (5)=\dfrac{\log_5 (5)}{\log_5 (11)}=\dfrac{1}{b}\)
28)\(\log _{6} (55)\)
29)\(\log _{11}\left (\dfrac{6}{11} \right )\)
- Responder
-
\(\log _{11}\left (\dfrac{6}{11} \right )=\dfrac{\log _{11}\left (\frac{6}{11} \right )}{\log _{5}(11)}=\dfrac{\log _{5}(6)-\log _{5}(11)}{\log _{5}(11)}=\dfrac{a-b}{b}=\dfrac{a}{b}-1\)
Numérico
Para los siguientes ejercicios, use propiedades de logaritmos para evaluar sin usar calculadora.
30)\(\log _3 \left ( \dfrac{1}{9} \right )-3\log _3 (3)\)
31)\(6\log _8 (2)+\dfrac{\log _8 (64)}{3\log _8 (4)}\)
- Responder
-
\(3\)
32)\(2\log _9 (3)-4\log _9 (3)+\log _9 \left (\dfrac{1}{729} \right )\)
Para los siguientes ejercicios, utilice la fórmula de cambio de base para evaluar cada expresión como cociente de registros naturales. Use una calculadora para aproximar cada uno a cinco decimales.
33)\(\log _3 (22)\)
- Responder
-
\(2.81359\)
34)\(\log _8 (65)\)
35)\(\log _6 (5.38)\)
- Responder
-
\(0.93913\)
36)\(\log _4 \left (\dfrac{15}{2} \right )\)
37)\(\log _{\frac{1}{2}} (4.7)\)
- Responder
-
\(-2.23266\)
Extensiones
38) Utilice la regla de producto para logaritmos para encontrar todos los\(x\) valores de tal manera que\(\log _{12} (2x+6)+\log _{12} (x+2)=2\)
39) Usa la regla del cociente para logaritmos para encontrar todos los\(x\) valores de tal manera que\(\log _{6} (x+2)-\log _{6} (x-3)=1\)
- Responder
-
Reescribir como ecuación exponencial y resolver para\(x\):
\ (\ begin {alinear*}
6^1 &=\ frac {x+2} {x-3}\\
0 &=\ frac {x+2} {x-3} -6\\
0 &=\ frac {x+2} {x-3} -\ frac {6 (x-3)} {(x-3)}\\
0 &=\ frac {x+2-6x+18} {x-3}\\
0 &=\ frac {x-4} {x-3}\\
x &= 4
\ end {alinear*}\)Comprobando, encontramos que\(\log _6(4+2)-\log _6(4-3)=\log _6(6)-\log _6(1)\) está definido, entonces\(x=4\)
40) ¿Se puede derivar la propiedad de potencia de logaritmos de la propiedad de potencia de los exponentes usando la ecuación?\(b^x=m\)
41) Demostrar que\(\log_b(n)=\frac{1}{\log_b(n)}\) para cualquier número entero positivo\(b>1\) y\(n>1\)
- Responder
-
Dejar\(b\) y\(n\) ser enteros positivos mayores que\(1\)
.
42) Hace\(\log_{81}(2401)=\log_3(7)\)
4.6: Ecuaciones Exponenciales y Logarítmicas
El crecimiento descontrolado de la población puede modelarse con funciones exponenciales. Las ecuaciones resultantes de esas funciones exponenciales se pueden resolver para analizar y hacer predicciones sobre el crecimiento exponencial. En esta sección, aprenderemos técnicas para resolver funciones exponenciales.
Verbal
1) ¿Cómo se puede resolver una ecuación exponencial?
- Responder
-
Determine primero si la ecuación puede ser reescrita para que cada lado utilice la misma base. Si es así, los exponentes se pueden establecer iguales entre sí. Si la ecuación no puede ser reescrita para que cada lado utilice la misma base, entonces aplique el logaritmo a cada lado y use propiedades de logaritmos para resolver.
2) ¿Cuándo ocurre una solución extraña? ¿Cómo se puede reconocer una solución extraña?
3) ¿Cuándo se puede utilizar la propiedad uno-a-uno de logaritmos para resolver una ecuación? ¿Cuándo no se puede usar?
- Responder
-
La propiedad uno a uno se puede usar si ambos lados de la ecuación se pueden reescribir como un logaritmo único con la misma base. Si es así, los argumentos se pueden establecer iguales entre sí, y la ecuación resultante se puede resolver algebraicamente. La propiedad uno a uno no se puede usar cuando cada lado de la ecuación no se puede reescribir como un solo logaritmo con la misma base.
Algebraico
Para los siguientes ejercicios, use como bases para resolver la ecuación exponencial.
4)\(4^{-3v-2}=4^{-v}\)
5)\(64\cdot 4^{3x}=16\)
- Responder
-
\(x=-\dfrac{1}{3}\)
6)\(3^{2x+1}\cdot 3^x=243\)
7)\(2^{-3n}\cdot \dfrac{1}{4}=2^{n+2}\)
- Responder
-
\(n=-1\)
8)\(625\cdot 5^{3x+3}=125\)
9)\(\frac{36^{3b}}{36^{2b}}=216^{2-b}\)
- Responder
-
\(b=\dfrac{6}{5}\)
10)\(\left (\dfrac{1}{64} \right )^{3n}\cdot 8=2^6\)
Para los siguientes ejercicios, usa logaritmos para resolver.
11)\(9^{x-10}=1\)
- Responder
-
\(x=10\)
12)\(2e^{6x}=13\)
13)\(e^{r+10}-10=-42\)
- Responder
-
Sin solución
14)\(2\cdot 10^{9a}=29\)
15)\(-8\cdot 10^{p+7}-7=-24\)
- Responder
-
\(p=\log \left (\frac{17}{8} \right )-7\)
16)\(7e^{3n-5}+5=-89\)
17)\(e^{-3k}+6=44\)
- Responder
-
\(k=-\frac{\ln(38)}{3}\)
18)\(-5e^{9x-8}-8=-62\)
19)\(-6e^{9x+8}+2=-74\)
- Responder
-
\(x=\frac{\frac{\ln(38)}{3}-8}{9}\)
20)\(2^{x+1}=5^{2x-1}\)
21)\(e^{2x}-e^{x}-132=0\)
- Responder
-
\(x=\ln 12\)
22)\(7e^{8x+8}-5=-95\)
23)\(10e^{8x+3}+2=8\)
- Responder
-
\(x=\frac{\frac{\ln(3)}{5}-3}{8}\)
24)\(4e^{3x+3}-7=53\)
25)\(8e^{-5x-2}-4=-90\)
- Responder
-
Sin solución
26)\(3^{2x+1}=7^{x-2}\)
27)\(e^{2x}-e^{x}-6=0\)
- Responder
-
\(x=\ln 3\)
28)\(3e^{3-3x}+6=-31\)
Para los siguientes ejercicios, utilice la definición de un logaritmo para reescribir la ecuación como una ecuación exponencial.
29)\(\log \left ( \frac{1}{100} \right )=-2\)
- Responder
-
\(10^{-2}=\dfrac{1}{100}\)
30)\(\log _{324}(18)=\dfrac{1}{2}\)
Para los siguientes ejercicios, utilice la definición de un logaritmo para resolver la ecuación.
31)\(5\log _{7}n=10\)
- Responder
-
\(n=49\)
32)\(-8\log _{9}x=16\)
33)\(4+\log _{2}(9k)=2\)
- Responder
-
\(k=\dfrac{1}{36}\)
34)\(2\log (8n+4)+6=10\)
35)\(10-4\ln (9-8x)=6\)
- Responder
-
\(x=\dfrac{9-e}{8}\)
Para los siguientes ejercicios, use la propiedad uno-a-uno de logaritmos para resolver.
36)\(\ln (10-3x)=\ln (-4x)\)
37)\(\log_{13} (5n-2)=\log_{13} (8-5n)\)
- Responder
-
\(n=1\)
38)\(\log (x+3)-\log (x)=\log (74)\)
39)\(\ln (-3x)=\ln (x^2-6x)\)
- Responder
-
Sin solución
40)\(\log_4 (6-m)=\log_4 (3m)\)
41)\(\ln (x-2)-\ln (x)=\ln (54)\)
- Responder
-
Sin solución
42)\(\log_9 (2n^2-14n)=\log_9 (-45+n^2)\)
43)\(\ln (x^2-10)+\ln (9)=\ln (10)\)
- Responder
-
\(x=\pm \frac{10}{3}\)
Para los siguientes ejercicios, resuelve cada ecuación para\(x\).
44)\(\log (x+12)=\log (x)+\log (12)\)
45)\(\ln (x)+\ln (x-3)=\ln (7x)\)
- Responder
-
\(x=10\)
46)\(\log_2 (7x+6)=3\)
47)\(\ln (7)+\ln (2-4x^2)=\ln (14)\)
- Responder
-
\(x=0\)
48)\(\log_8 (x+6)-\log_8 (x)=\log_8 (58)\)
49)\(\ln (3)-\ln (3-3x)=\ln (4)\)
- Responder
-
\(x=\dfrac{3}{4}\)
50)\(\log_3 (3x)-\log_3 (6)=\log_3 (77)\)
Gráfica
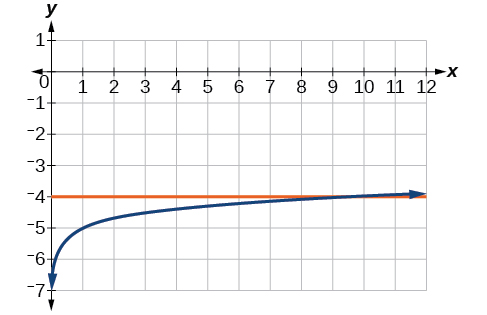
Para los siguientes ejercicios, resuelve la ecuación para\(x\)
51)\(\log_9 (x)-5=-4\)
- Responder
-
\(x=9\)
52)\(\log_3 (x)+3=2\)
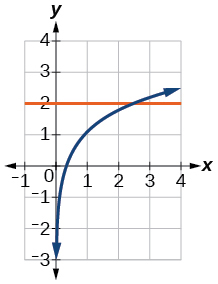
53)\(\ln (3x)=2\)
- Responder
-
\(x=\dfrac{e^2}{3}\approx 2.5\)
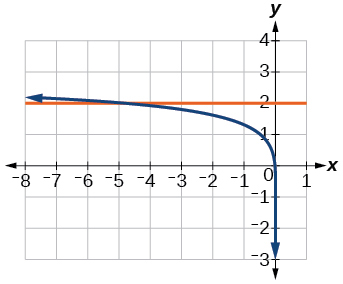
54)\(\ln (x-5)=1\)
55)\(\log (4)+\log (-5x)=2\)
- Responder
-
\(x=-5\)
56)\(-7+\log_3 (4-x)=-6\)
57)\(\ln (4x-10)-6=-5\)
- Responder
-
\(x=\dfrac{e+10}{4}\approx 3.2\)
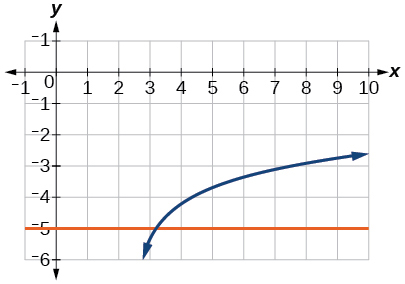
58)\(\log (4-2x)=\log (-4x)\)
59)\(\log_{11} (-2x^2 -7x)=\log_{11} (x-2)\)
- Responder
-
Sin solución
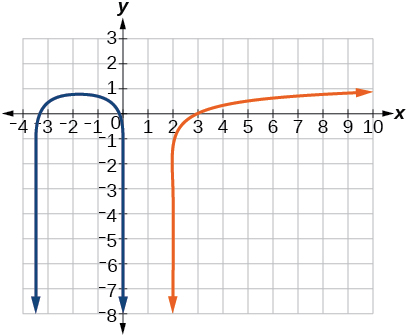
60)\(\ln (2x+9)=\ln (-5x)\)
61)\(\log_9 (3-x)=\log_9 (4x-8)\)
- Responder
-
\(x=\dfrac{11}{5}\approx 2.2\)
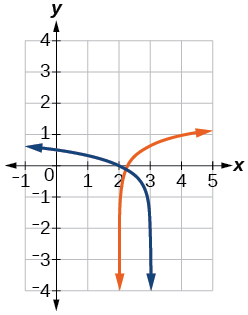
62)\(\log (x^2+13)=\log (7x+3)\)
63)\(\dfrac{3}{\log _2(10)}-\log (x-9)=\log (44)\)
- Responder
-
\(x=\dfrac{101}{11}\approx 9.2\)
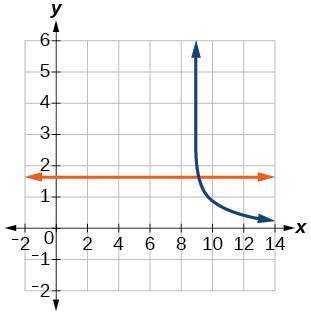
64)\(\ln (x)-\ln (x+3)=\ln (6)\)
Para los siguientes ejercicios, resuelva para el valor indicado, y grafique la situación mostrando el punto de solución.
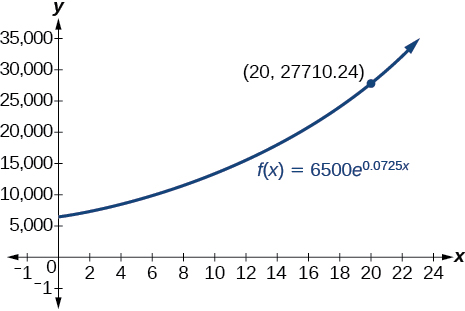
65) Una cuenta con un depósito inicial de\(\$6,500\) gana intereses\(7.25\%\) anuales, compuestos continuamente. ¿Cuánto valdrá la cuenta después de\(20\) años?
- Responder
-
acerca de\(\$27,710.24\)
66) La fórmula para medir la intensidad del sonido en decibelios\(D\) se define por la ecuación\(D=10\log \left ( \frac{I}{I_0} \right )\)
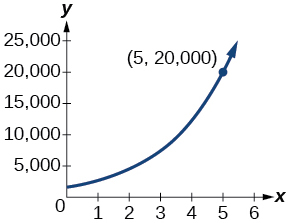
67) La población de un pueblo pequeño es modelada por la ecuación\(P=1650e^{0.5t}\) donde\(t\) se mide en años. ¿En aproximadamente cuántos años llegará la población del pueblo\(20,000\)?
- Responder
-
acerca de\(5\) años
Tecnología
Para los siguientes ejercicios, resuelve cada ecuación reescribiendo la expresión exponencial usando el logaritmo indicado. Luego usa una calculadora para aproximar la variable a lugares\(3\) decimales.
68)\(1000(1.03)^t=5000\) utilizando el registro común.
69)\(e^{5x}=17\) utilizando el tronco natural.
- Responder
-
\(\dfrac{\ln (17)}{5}\approx 0.567\)
70)\(3(1.04)^{3t}=8\) usando el registro común
71)\(3^{4x-5}=38\) usando el registro común
- Responder
-
\(x=\dfrac{\log (38+5\log (3))}{4\log(3)}\approx 2.078\)
72)\(50e^{-0.12t}=10\) utilizando el tronco natural
Para los siguientes ejercicios, utilice una calculadora para resolver la ecuación. A menos que se indique lo contrario, redondear todas las respuestas a la diez milésima más cercana.
73)\(7e^{3x-5}+7.9=47\)
- Responder
-
\(x\approx 2.2401\)
74)\(\ln (3)+\ln (4.4x+6.8)=2\)
75)\(\log(-0.7x-9)=1+5\log(5)\)
- Responder
-
\(x\approx -44655.7143\)
76) La presión atmosférica\(P\) en libras por pulgada cuadrada está representada por la fórmula\(P=14.7e^{-0.21x}\)
77) La magnitud\(M\) de un sismo está representada por la ecuación\(M=\dfrac{2}{3}\log \left ( \dfrac{E}{E_0} \right )\) donde\(E\) está la cantidad de energía liberada por el sismo en julios\(E_0=10^{4.4}\) y es la medida mínima asignada liberada por un sismo. A la centésima más cercana, ¿cuál sería la magnitud de un sismo liberando\(1.4\cdot 10^{13}\) julios de energía?
- Responder
-
acerca de\(5.83\)
Extensiones
78) Utilizar la definición de logaritmo junto con la propiedad uno-a-uno de logaritmos para demostrarlo\(b^{\log_b x}=x\).
79) Recordemos la fórmula para capitalizar continuamente los intereses,\(y=Ae^{kt}\)
- Responder
-
\(t=\ln \left ( \left ( \dfrac{y}{A} \right )^{\frac{1}{k}} \right )\)
80) Recordemos la fórmula de interés compuesto\(A=a\left ( 1+\frac{r}{k} \right )^{kt}\)
81) La Ley de Enfriamiento de Newton establece que la temperatura\(T\) de un objeto en cualquier momento\(t\) puede ser descrita por la ecuación\(T=T_s+(T_0-T_s)e^{-kt}\)
- Responder
-
\(t=\ln \left ( \left ( \frac{T-T_s}{T_0-T_s} \right )^{-\frac{1}{k}} \right )\)
4.7: Modelos Exponenciales y Logarítmicos
Ya hemos explorado algunas aplicaciones básicas de funciones exponenciales y logarítmicas. En esta sección, exploramos algunas aplicaciones importantes en mayor profundidad, incluyendo los isótopos radiactivos y la Ley de Enfriamiento de Newton.
Verbal
1) ¿Con qué tipo de modelo exponencial se asociaría la vida media? ¿Qué papel juega la vida media en estos modelos?
- Responder
-
La vida media es una medida de decadencia y, por lo tanto, se asocia con modelos de decaimiento La vida media de una sustancia o cantidad es la cantidad de tiempo que tarda la mitad de la cantidad inicial de esa sustancia o cantidad en decairse.
2) ¿Qué es la datación por carbono? ¿Por qué funciona? Dé un ejemplo en el que sería útil la datación por carbono.
3) ¿Con qué tipo de modelo exponencial se asociaría duplicar el tiempo? ¿Qué papel juega la duplicación del tiempo en estos modelos?
- Responder
-
El tiempo de duplicación es una medida del crecimiento y, por lo tanto, se asocia con modelos de crecimiento exponencial. El tiempo de duplicación de una sustancia o cantidad es la cantidad de tiempo que toma para que la cantidad inicial de esa sustancia o cantidad duplique su tamaño.
4) Definir la Ley de Enfriamiento de Newton. Entonces nombra al menos tres situaciones del mundo real donde se aplicaría la Ley de Enfriamiento de Newton.
5) ¿Qué es un orden de magnitud? ¿Por qué son útiles los órdenes de magnitud? Dar un ejemplo para explicar.
- Responder
-
Un orden de magnitud es la potencia más cercana de diez por la cual una cantidad crece exponencialmente. También es una posición aproximada en una escala logarítmica; Respuesta muestral: Los órdenes de magnitud son útiles a la hora de hacer comparaciones entre números que difieren en gran cantidad. Por ejemplo, la masa de Saturno es\(95\) veces mayor que la masa de la Tierra. Esto es lo mismo que decir que la masa de Saturno es aproximadamente\(10^2\) veces, u\(2\) órdenes de magnitud mayor, que la masa de la Tierra.
Numérico
6) La temperatura de un objeto en grados Fahrenheit después de\(t\) minutos se representa por la ecuación\(T(t)=68e^{-0.0174t}+72\)
Para los siguientes ejercicios, utilice el modelo de crecimiento logístico \(f(x)=\dfrac{150}{1+8e^{-2x}}\)
7) Buscar e interpretar\(f(0)\)
- Responder
-
\(f(0)\approx 16.7\); La cantidad inicialmente presente es sobre\(16.7\) unidades.
8) Buscar e interpretar\(f(4)\)
9) Encuentra la capacidad de carga.
- Responder
-
\(150\)
10) Graficar el modelo.
11) Determinar si los datos de la tabla podrían representarse mejor como una función lineal, exponencial o logarítmica. Después escribe una fórmula para un modelo que represente los datos.
| \(x\) | \(f(x)\) |
|---|---|
| \ (x\) ">—2 | \ (f (x)\) ">0.694 |
| \ (x\) ">—1 | \ (f (x)\) ">0.833 |
| \ (x\) ">0 | \ (f (x)\) ">1 |
| \ (x\) ">1 | \ (f (x)\) ">1.2 |
| \ (x\) ">2 | \ (f (x)\) ">1.44 |
| \ (x\) ">3 | \ (f (x)\) ">1.728 |
| \ (x\) ">4 | \ (f (x)\) ">2.074 |
| \ (x\) ">5 | \ (f (x)\) ">2.488 |
- Responder
-
exponencial;\(f(x)=1.2^x\)
12) Reescribir\(f(x)=1.68(0.65)^x\) como una ecuación exponencial con base\(e\) a cinco dígitos significativos.
Tecnología
Para los siguientes ejercicios, ingrese los datos de cada tabla en una calculadora gráfica y grafique las gráficas de dispersión resultantes. Determine si los datos de la tabla podrían representar una función lineal, exponencial o logarítmica.
13)
| \(x\) | \(f(x)\) |
|---|---|
| \ (x\) ">1 | \ (f (x)\) ">2 |
| \ (x\) ">2 | \ (f (x)\) ">4.079 |
| \ (x\) ">3 | \ (f (x)\) ">5.296 |
| \ (x\) ">4 | \ (f (x)\) ">6.159 |
| \ (x\) ">5 | \ (f (x)\) ">6.828 |
| \ (x\) ">6 | \ (f (x)\) ">7.375 |
| \ (x\) ">7 | \ (f (x)\) ">7.838 |
| \ (x\) ">8 | \ (f (x)\) ">8.238 |
| \ (x\) ">9 | \ (f (x)\) ">8.592 |
| \ (x\) ">10 | \ (f (x)\) ">8.908 |
- Responder
-
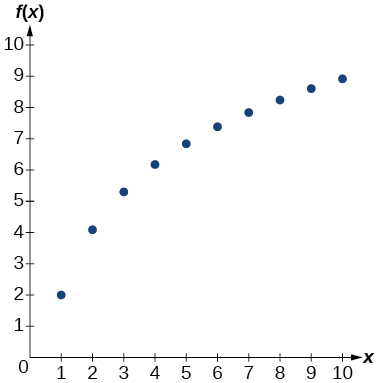
14)
| \(x\) | \(f(x)\) |
|---|---|
| \ (x\) ">1 | \ (f (x)\) ">2.4 |
| \ (x\) ">2 | \ (f (x)\) ">2.88 |
| \ (x\) ">3 | \ (f (x)\) ">3.456 |
| \ (x\) ">4 | \ (f (x)\) ">4.147 |
| \ (x\) ">5 | \ (f (x)\) ">4.977 |
| \ (x\) ">6 | \ (f (x)\) ">5.972 |
| \ (x\) ">7 | \ (f (x)\) ">7.166 |
| \ (x\) ">8 | \ (f (x)\) ">8.6 |
| \ (x\) ">9 | \ (f (x)\) ">10.32 |
| \ (x\) ">10 | \ (f (x)\) ">12.383 |
15)
| \(x\) | \(f(x)\) |
|---|---|
| \ (x\) ">4 | \ (f (x)\) ">9.429 |
| \ (x\) ">5 | \ (f (x)\) ">9.972 |
| \ (x\) ">6 | \ (f (x)\) ">10.415 |
| \ (x\) ">7 | \ (f (x)\) ">10.79 |
| \ (x\) ">8 | \ (f (x)\) ">11.115 |
| \ (x\) ">9 | \ (f (x)\) ">11.401 |
| \ (x\) ">10 | \ (f (x)\) ">11.657 |
| \ (x\) ">11 | \ (f (x)\) ">11.889 |
| \ (x\) ">12 | \ (f (x)\) ">12.101 |
| \ (x\) ">13 | \ (f (x)\) ">12.295 |
- Responder
-
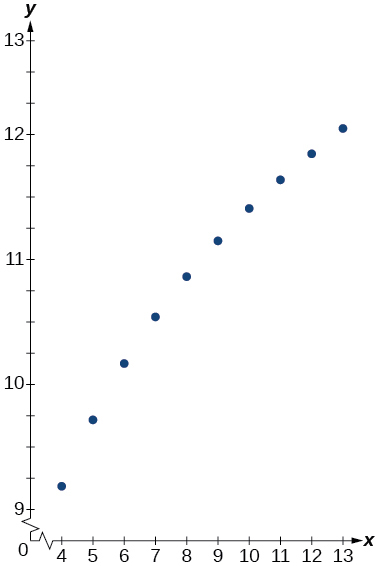
16)
| \(x\) | \(f(x)\) |
|---|---|
| \ (x\) ">1.25 | \ (f (x)\) ">5.75 |
| \ (x\) ">2.25 | \ (f (x)\) ">8.75 |
| \ (x\) ">3.56 | \ (f (x)\) ">12.68 |
| \ (x\) ">4.2 | \ (f (x)\) ">14.6 |
| \ (x\) ">5.65 | \ (f (x)\) ">18.95 |
| \ (x\) ">6.75 | \ (f (x)\) ">22.25 |
| \ (x\) ">7.25 | \ (f (x)\) ">23.75 |
| \ (x\) ">8.6 | \ (f (x)\) ">27.8 |
| \ (x\) ">9.25 | \ (f (x)\) ">29.75 |
| \ (x\) ">10.5 | \ (f (x)\) ">33.5 |
Para los siguientes ejercicios, utilice una calculadora gráfica y este escenario: la población de una piscifactoría en\(t\) años se modela por la ecuación\(P(t)=\dfrac{1000}{1+9e^{-0.6t}}\)
17) Graficar la función.
- Responder
-
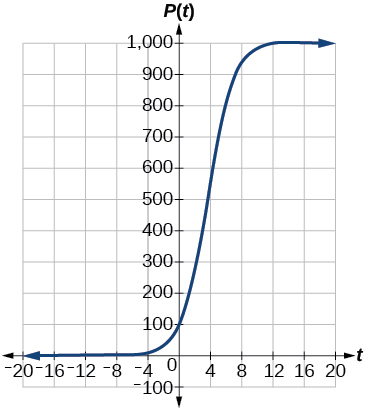
18) ¿Cuál es la población inicial de peces?
19) Al décimo más cercano, ¿cuál es el tiempo de duplicación para la población de peces?
- Responder
-
acerca de\(1.4\) años
20) Al número entero más cercano, ¿cuál será la población de peces después de\(2\) años?
21) A la décima más cercana, ¿cuánto tiempo tardará la población en llegar\(900\)?
- Responder
-
acerca de\(7.3\) años
22) ¿Cuál es la capacidad de carga de la población de peces? Justifica tu respuesta usando la gráfica de\(P\).
Extensiones
23) Una sustancia tiene una vida media de\(2.045\) minutos. Si la cantidad inicial de la sustancia era\(132.8\) gramos, ¿cuántas vidas medias habrán pasado antes de que la sustancia se descomponga a\(8.3\) gramos? ¿Cuál es el tiempo total de decaimiento?
- Responder
-
\(4\)vidas medias;\(8.18\) minutos
24) La fórmula para una población creciente viene dada por\(P(t)=P_0e^{rt}\) dónde\(P_0\) está la población inicial y\(r>0\)
25) Recordemos la fórmula para calcular la magnitud de un sismo,\(M=\dfrac{2}{3}\log \left ( \dfrac{S}{S_0} \right )\)
- Responder
-
\(\begin{align*} M&= \dfrac{2}{3}\log \left ( \dfrac{S}{S_0} \right )\\ \log \left ( \dfrac{S}{S_0} \right )&= \dfrac{3}{2}M\\ \dfrac{S}{S_0}&= 10^{\frac{3M}{2}}\\ S&= S_0 10^{\frac{3M}{2}} \end{align*}\)
26) Cuál es la\(y\) intercepción del modelo de crecimiento logístico\(y=\dfrac{c}{1+ae^{-rx}}\)
27) Demostrarlo\(b^x=e^{x\ln (b)}\) para positivo\(b≠1\).
- Responder
-
Dejar que\(y=b^x\) para algún número real no negativo\(b\) tal que\(b\neq1\)
. \(\begin{align*} \ln (y) &= \ln (b^x)\\ \ln (y) &= x\ln (b)\\ e^{\ln (y)} &= e^{x\ln (b)}\\ y&= e^{x\ln (b)} \end{align*}\)
Aplicaciones del mundo real
Para los siguientes ejercicios, use este escenario: Un médico prescribe\(125\) miligramos de un medicamento terapéutico que decae aproximadamente\(30\%\) cada hora.
28) A la hora más cercana, ¿cuál es la vida media de la droga?
29) Escribir un modelo exponencial que represente la cantidad del medicamento restante en el sistema del paciente después de\(t\) horas. Luego usa la fórmula para encontrar la cantidad del medicamento que quedaría en el sistema del paciente después de\(3\) horas. Redondear al miligramo más cercano.
- Responder
-
\(A=125e^{(-0.3567t)}\);\(A\approx 43\) mg
30) Utilizando el modelo encontrado en el ejercicio anterior, encontrar\(f(10\) e interpretar el resultado. Redondear a la centésima más cercana.
Para los siguientes ejercicios, utilice este escenario: A un tumor se le inyectan\(0.5\) gramos de yodo-125, el cual tiene una tasa de decaimiento\(1.15\%\) por día.
31) Al día más cercano, ¿cuánto tiempo tardará en decairse la mitad del yodo-125?
- Responder
-
acerca de\(60\) días
32) Escribir un modelo exponencial que represente la cantidad de yodo-125 restante en el tumor después de\(t\) días. Luego usa la fórmula para encontrar la cantidad de yodo-125 que quedaría en el tumor después de\(60\) días. Redondear a la décima de gramo más cercana.
33) Un científico comienza con\(250\) gramos de una sustancia radiactiva. Después de\(250\) minutos, la muestra ha decaído a\(32\) gramos. Redondeando a cinco dígitos significativos, escribir una ecuación exponencial que represente esta situación. Al minuto más cercano, ¿cuál es la vida media de esta sustancia?
- Responder
-
\(f(t)=250e^{(-0.00914t)}\)
;
34) La vida media del Radio-226 es de\(1590\) años. ¿Cuál es la tasa de decaimiento anual? Exprese el resultado decimal a cuatro dígitos significativos y el porcentaje a dos dígitos significativos.
35) La vida media del Erbio-165 es de\(10.4\) horas. ¿Cuál es la tasa de decaimiento horario? Exprese el resultado decimal a cuatro dígitos significativos y el porcentaje a dos dígitos significativos.
- Responder
-
\(r\approx -0.0667\)
,
36) Un artefacto de madera de una excavación arqueológica contiene\(60\) por ciento del carbono-14 que está presente en los árboles vivos. Al año más cercano, ¿de cuántos años tiene el artefacto? (La vida media del carbono-14 es\(5730\) años.)
37) Un estudiante de investigación está trabajando con un cultivo de bacterias que duplica su tamaño cada veinte minutos. El recuento poblacional inicial fue\(1350\) bacteriano. Redondeando a cinco dígitos significativos, escribir una ecuación exponencial que represente esta situación. Al número entero más cercano, ¿cuál es el tamaño de la población después de\(3\) horas?
- Responder
-
\(f(t)=1350e^{(0.03466t)}\); después del\(3\) horario:\(P(180)\approx 691,200\)
Para los siguientes ejercicios, utilice este escenario: Un biólogo registró un recuento de\(360\) bacterias presentes en un cultivo después de\(5\) minutos y\(1000\) bacterias presentes después de\(20\) minutos.
38) Al número entero más cercano, ¿cuál fue la población inicial en la cultura?
39) Redondeando a seis dígitos significativos, escribir una ecuación exponencial que represente esta situación. Al minuto más cercano, ¿cuánto tiempo tardó la población en duplicar?
- Responder
-
\(f(t)=256e^{(0.068110t)}\); tiempo de duplicación: aproximadamente\(10\) minutos
Para los siguientes ejercicios, usa este escenario: Se sacó de la estufa una olla de sopa hirviendo con una temperatura interna de\(100^{\circ}\) Fahrenheit para enfriarse en una habitación\(69^{\circ}\) F. Después de quince minutos, la temperatura interna de la sopa era\(95^{\circ}\) F.
40) Usa la Ley de Enfriamiento de Newton para escribir una fórmula que modele esta situación.
41) Al minuto más cercano, ¿cuánto tiempo tardará la sopa en enfriarse a\(80^{\circ}\) F?
- Responder
-
acerca de\(88\) minutos
42) Al grado más cercano, ¿cuál será la temperatura después de horas\(2\) y media?
Para los siguientes ejercicios, usa este escenario: Un pavo se saca del horno con una temperatura interna de\(165^{\circ}\) F y se deja enfriar en una habitación\(75^{\circ}\) F. Después de media hora, la temperatura interna del pavo es\(145^{\circ}\) F.
43) Escribir una fórmula que modele esta situación.
- Responder
-
\(T(t)=90e^{(-0.008377t)}+75\), donde\(t\) está en minutos.
44) Al grado más cercano, ¿cuál será la temperatura después de\(50\) minutos?
45) Al minuto más cercano, ¿cuánto tiempo tardará el pavo en enfriarse a\(110^{\circ}\) F?
- Responder
-
acerca de\(113\) minutos
Para los siguientes ejercicios, encuentra el valor del número mostrado en cada escala logarítmica. Redondear todas las respuestas a la milésima más cercana.

- Responder
-
\(\log(x)=1.5; x\approx 31.623\)
48) Trazar cada conjunto de valores aproximados de intensidad de sonidos en una escala logarítmica: Susurro:\(10^{-10}\dfrac{W}{m^2}\)
49) Recordemos la fórmula para calcular la magnitud de un sismo,\(M=\dfrac{2}{3}\log \left ( \dfrac{S}{S_0} \right )\)
- Responder
-
Magnitud de MMS:\(5.82\)
Para los siguientes ejercicios, usa este escenario: La ecuación\(N(t)=\dfrac{500}{1+49e^{-0.7t}}\) modela el número de personas en un pueblo que han escuchado un rumor después de\(t\) días.
50) ¿Cuánta gente empezó el rumor?
51) Al número entero más cercano, ¿cuántas personas habrán escuchado el rumor después de\(3\) días?
- Responder
-
\(N(3)\approx 71\)
52) Como t
Para el siguiente ejercicio, elija la opción de respuesta correcta.
53) Un médico e inyecta a un paciente\(13\) miligramos de tinte radiactivo que se descompone exponencialmente. Después de\(12\) minutos, quedan\(4.75\) miligramos de tinte en el sistema del paciente. ¿Cuál es un modelo apropiado para esta situación?
- \(f(t)=13(0.0805)^t\)
- \(f(t)=13e^{0.9195t}\)
- \(f(t)=13e^{(-0.0839t)}\)
- \(f(t)=\frac{4.75}{1+13e^{-0.83925t}}\)
- Responder
-
c
4.8: Ajuste de modelos exponenciales a los datos
Nos concentraremos en tres tipos de modelos de regresión en esta sección: exponencial, logarítmico y logístico. Haber trabajado ya con cada una de estas funciones nos da una ventaja. Conocer sus definiciones formales, el comportamiento de sus gráficas y algunas de sus aplicaciones del mundo real nos da la oportunidad de profundizar en nuestra comprensión. A medida que se presenta cada modelo de regresión, se incluyen características clave y definiciones de su función asociada para su revisión.
Verbal
1) ¿Qué situaciones se modelan mejor con una ecuación logística? Dar un ejemplo, y exponer un caso de por qué el ejemplo es un buen ajuste.
- Responder
-
Los modelos logísticos se utilizan mejor para situaciones que tienen valores limitados. Por ejemplo, las poblaciones no pueden crecer indefinidamente ya que los recursos como los alimentos, el agua y el espacio son limitados, por lo que un modelo logístico describe mejor a las poblaciones.
2) ¿Qué es una capacidad de carga? ¿Qué tipo de modelo tiene una capacidad de carga incorporada en su fórmula? ¿Por qué tiene sentido esto?
3) ¿Qué es el análisis de regresión? Describir el proceso de análisis de regresión en una utilidad gráfica.
- Responder
-
El análisis de regresión es el proceso de encontrar una ecuación que mejor se ajuste a un conjunto dado de puntos de datos. Para realizar un análisis de regresión en una utilidad gráfica, primero enumere los puntos dados usando el menú STAT y luego EDITAR. A continuación grafica la gráfica de dispersión usando la función STAT PLOT. La forma de los puntos de datos en el gráfico de dispersión puede ayudar a determinar qué característica de regresión usar. Una vez determinado esto, seleccione el comando de análisis de regresión apropiado en el menú STAT y luego CALC.
4) ¿Cómo podría ser una gráfica de dispersión de puntos de datos si fuera mejor descrita por un modelo logarítmico?
5) ¿A qué corresponde la intersección y en la gráfica de una ecuación logística para una población modelada por esa ecuación?
- Responder
-
El\(y\) -intercepto en la gráfica de una ecuación logística corresponde a la población inicial para el modelo poblacional.
Gráfica
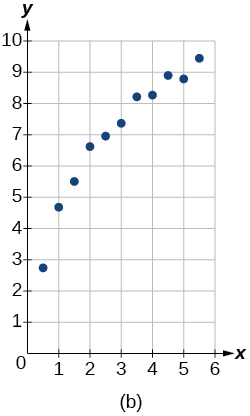
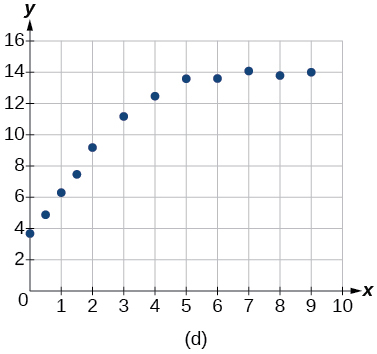
Para los siguientes ejercicios, haga coincidir la función dada de mejor ajuste con la gráfica de dispersión apropiada de la Figura (a) a la Figura (e). Contesta usando la letra debajo de la gráfica coincidente.
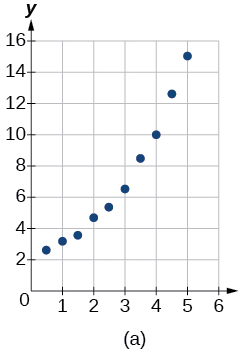
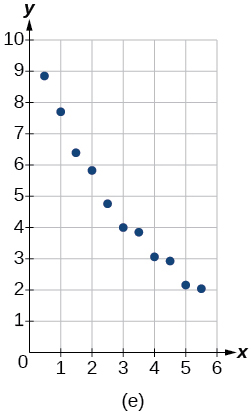
6)\(y=10.209e^{-0.294x}\)
7)\(y=5.598-1.912\ln (x)\)
- Responder
-
c
8)\(y=2.104(1.479)^x\)
9)\(y=4.607+2.733\ln (x)\)
- Responder
-
b
10)\(y=\dfrac{14.005}{1+2.79e^{-0.812x}}\)
Numérico
11) Al número entero más cercano, cuál es el valor inicial de una población modelada por la ecuación logística\(P(t)=\dfrac{175}{1+6.995e^{-0.68t}}\)
- Responder
-
\(P(0)=22\);\(175\)
12) Reescribir el modelo exponencial\(A(t)=1550(1.085)^x\) como un modelo equivalente con base\(e\)
13) Un modelo logarítmico viene dado por la ecuación\(h(p)=67.682-5.792\ln (p)\)
- Responder
-
\(p\approx 2.67\)
14) Un modelo logístico viene dado por la ecuación\(P(t)=\dfrac{90}{1+5e^{-0.42t}}\)
15) ¿Cuál es la\(y\) -intercepción en la gráfica del modelo logístico dado en el ejercicio anterior?
- Responder
-
\(y\)-interceptar:\((0,15)\)
Tecnología
Para los siguientes ejercicios, utilice este escenario: La población\(P\) de un estanque koi a lo largo de\(x\) meses está modelada por la función\(P(x)=\dfrac{68}{1+16e^{-0.28x}}\).
16) Graficar el modelo poblacional para mostrar la población a lo largo de un lapso de\(3\) años.
17) ¿Cuál fue la población inicial de koi?
- Responder
-
\ (4)\ koi
18) ¿Cuántos koi tendrá el estanque después de un año y medio?
19) ¿Cuántos meses tardarán antes de que haya\(20\) koi en el estanque?
- Responder
-
acerca de los\(6.8\) meses
20) Utilizar la función de intersección para aproximar el número de meses que tardará antes de que la población del estanque alcance la mitad de su capacidad de carga.
- Responder
-
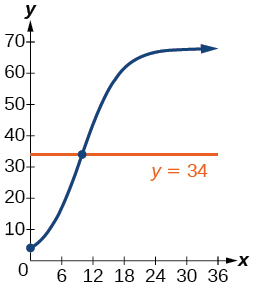
Para los siguientes ejercicios, utilice este escenario: La población\(P\) de una especie en peligro de extinción hábitat para lobos es modelada por la función\(P(x)=\dfrac{558}{1+54.8e^{-0.462x}}\)
21) Graficar el modelo poblacional para mostrar la población a lo largo de un lapso de\(10\) años.
22) ¿Cuál fue la población inicial de lobos transportados al hábitat?
- Responder
-
\ (10)\ lobos
23) ¿Cuántos lobos tendrá el hábitat después de\(3\) años?
24) ¿Cuántos años pasarán antes de que haya\(100\) lobos en el hábitat?
- Responder
-
acerca de\(5.4\) años
25) Utilizar la característica de intersección para aproximar el número de años que tardará antes de que la población del hábitat alcance la mitad de su capacidad de carga.
Para los siguientes ejercicios, consulte la Tabla a continuación.
| \(x\) | \(f(x)\) |
|---|---|
| \ (x\) ">1 | \ (f (x)\) ">1125 |
| \ (x\) ">2 | \ (f (x)\) ">1495 |
| \ (x\) ">3 | \ (f (x)\) ">2310 |
| \ (x\) ">4 | \ (f (x)\) ">3294 |
| \ (x\) ">5 | \ (f (x)\) ">4650 |
| \ (x\) ">6 | \ (f (x)\) ">6361 |
26) Utilice una calculadora gráfica para crear un diagrama de dispersión de los datos.
- Responder
-
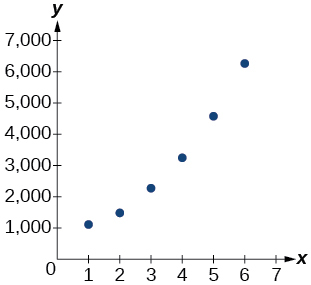
27) Utilice la función de regresión para encontrar una función exponencial que mejor se ajuste a los datos de la tabla.
28) Escribir la función exponencial como una ecuación exponencial con base\(e\)
- Responder
-
\(f(x)=776.682e^{0.3549x}\)
29) Grafique la ecuación exponencial en el diagrama de dispersión.
30) Utilice la función de intersección para encontrar el valor de\(x\) para cuál\(f(x)=4000\).
- Responder
-
Cuando\(f(x)=4000\),\(x\approx 4.6\)
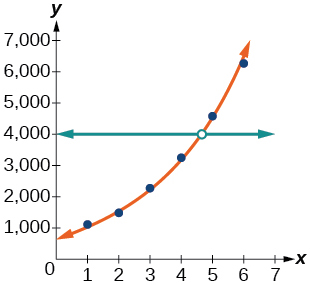
Para los siguientes ejercicios, consulte la Tabla a continuación.
| \(x\) | \(f(x)\) |
|---|---|
| \ (x\) ">1 | \ (f (x)\) ">555 |
| \ (x\) ">2 | \ (f (x)\) ">383 |
| \ (x\) ">3 | \ (f (x)\) ">307 |
| \ (x\) ">4 | \ (f (x)\) ">210 |
| \ (x\) ">5 | \ (f (x)\) ">158 |
| \ (x\) ">6 | \ (f (x)\) ">122 |
31) Utilice una calculadora gráfica para crear un diagrama de dispersión de los datos.
32) Utilice la función de regresión para encontrar una función exponencial que mejor se ajuste a los datos de la tabla.
- Responder
-
\(f(x)=731.92(0.738)^x\)
33) Escribir la función exponencial como una ecuación exponencial con base\(e\)
34) Grafica la ecuación exponencial en el diagrama de dispersión.
- Responder
-
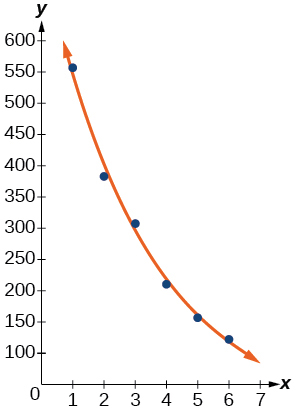
35) Utilice la función de intersección para encontrar el valor\(x\) para el cual\(f(x)=250\)
Para los siguientes ejercicios, consulte la Tabla a continuación.
| \(x\) | \(f(x)\) |
|---|---|
| \ (x\) ">1 | \ (f (x)\) ">5.1 |
| \ (x\) ">2 | \ (f (x)\) ">6.3 |
| \ (x\) ">3 | \ (f (x)\) ">7.3 |
| \ (x\) ">4 | \ (f (x)\) ">7.7 |
| \ (x\) ">5 | \ (f (x)\) ">8.1 |
| \ (x\) ">6 | \ (f (x)\) ">8.6 |
36) Utilice una calculadora gráfica para crear un diagrama de dispersión de los datos.
- Responder
-
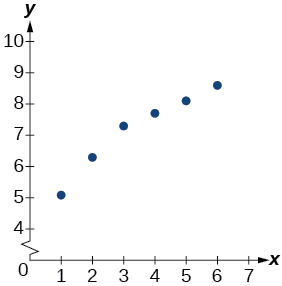
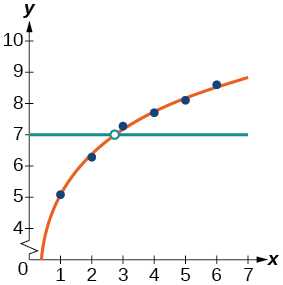
37) Utilice la opción Logaritmo de la función Regresión para encontrar una función logarítmica de la forma\(y=a+b\ln (x)\) que mejor se ajuste a los datos de la tabla.
38) Utilice la función logarítmica para encontrar el valor de la función cuando\(x=10\)
- Responder
-
\(f(10)\approx 9.5\)
39) Grafique la ecuación logarítmica en el diagrama de dispersión.
40) Utilice la función de intersección para encontrar el valor\(x\) para el cual\(f(x)=7\)
- Responder
-
Cuando\(f(x)=7\),\(x\approx 2.7\)
Para los siguientes ejercicios, consulte la Tabla a continuación.
| \(x\) | \(f(x)\) |
|---|---|
| \ (x\) ">1 | \ (f (x)\) ">7.5 |
| \ (x\) ">2 | \ (f (x)\) ">6 |
| \ (x\) ">3 | \ (f (x)\) ">5.2 |
| \ (x\) ">4 | \ (f (x)\) ">4.3 |
| \ (x\) ">5 | \ (f (x)\) ">3.9 |
| \ (x\) ">6 | \ (f (x)\) ">3.4 |
| \ (x\) ">7 | \ (f (x)\) ">3.1 |
| \ (x\) ">8 | \ (f (x)\) ">2.9 |
41) Utilice una calculadora gráfica para crear un diagrama de dispersión de los datos.
42) Utilice la opción Logaritmo de la función Regresión para encontrar una función logarítmica de la forma\(y=a+b\ln (x)\) que mejor se ajuste a los datos de la tabla.
- Responder
-
\(f(x)=7.544-2.268\ln (x)\)
43) Utilice la función logarítmica para encontrar el valor de la función cuando\(x=10\)
44) Grafique la ecuación logarítmica en el diagrama de dispersión.
- Responder
-
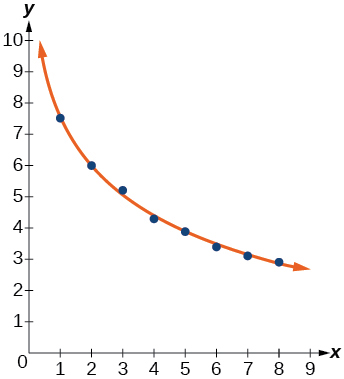
45) Utilice la función de intersección para encontrar el valor\(x\) para el cual\(f(x)=8\)
Para los siguientes ejercicios, consulte la Tabla a continuación.
| \(x\) | \(f(x)\) |
|---|---|
| \ (x\) ">1 | \ (f (x)\) ">8.7 |
| \ (x\) ">2 | \ (f (x)\) ">12.3 |
| \ (x\) ">3 | \ (f (x)\) ">15.4 |
| \ (x\) ">4 | \ (f (x)\) ">18.5 |
| \ (x\) ">5 | \ (f (x)\) ">20.7 |
| \ (x\) ">6 | \ (f (x)\) ">22.5 |
| \ (x\) ">7 | \ (f (x)\) ">23.3 |
| \ (x\) ">8 | \ (f (x)\) ">24 |
| \ (x\) ">9 | \ (f (x)\) ">24.6 |
| \ (x\) ">10 | \ (f (x)\) ">24.8 |
46) Utilice una calculadora gráfica para crear un diagrama de dispersión de los datos.
- Responder
-
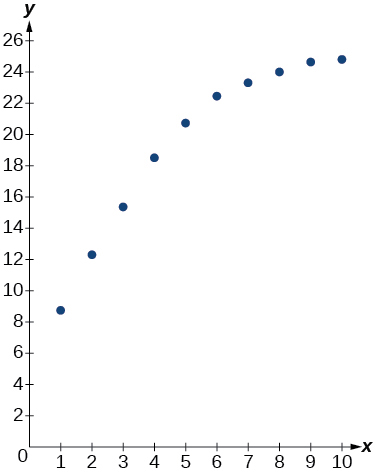
47) Utilice la opción de regresión LOGÍSTICA para encontrar un modelo de crecimiento logístico de la forma\(y=\dfrac{c}{1+ae^{-bx}}\) que mejor se ajuste a los datos de la tabla.
48) Graficar la ecuación logística en el diagrama de dispersión.
- Responder
-
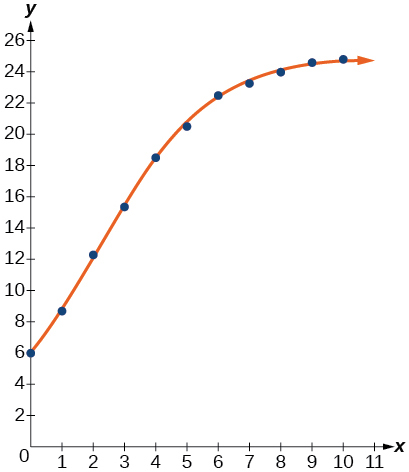
49) Al número entero más cercano, ¿cuál es la capacidad de carga prevista del modelo?
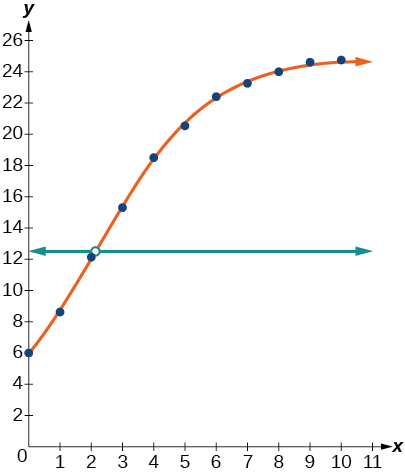
50) Utilice la función de intersección para encontrar el valor\(x\) para el cual el modelo alcanza la mitad de su capacidad de carga.
- Responder
-
Cuando\(f(x)=12.5\),\(x\approx 2.1\)
Para los siguientes ejercicios, consulte la Tabla a continuación.
| \(x\) | \(f(x)\) |
|---|---|
| \ (x\) ">0 | \ (f (x)\) ">12 |
| \ (x\) ">2 | \ (f (x)\) ">28.6 |
| \ (x\) ">4 | \ (f (x)\) ">52.8 |
| \ (x\) ">5 | \ (f (x)\) ">70.3 |
| \ (x\) ">7 | \ (f (x)\) ">99.9 |
| \ (x\) ">8 | \ (f (x)\) ">112.5 |
| \ (x\) ">10 | \ (f (x)\) ">125.8 |
| \ (x\) ">11 | \ (f (x)\) ">127.9 |
| \ (x\) ">15 | \ (f (x)\) ">135.1 |
| \ (x\) ">17 | \ (f (x)\) ">135.9 |
51) Utilice una calculadora gráfica para crear un diagrama de dispersión de los datos.
52) Utilice la opción de regresión LOGÍSTICA para encontrar un modelo de crecimiento logístico de la forma\(y=\dfrac{c}{1+ae^{-bx}}\) que mejor se ajuste a los datos de la tabla.
- Responder
-
\(y=\dfrac{136.068}{1+10.324e^{-0.480x}}\)
53) Graficar la ecuación logística en el diagrama de dispersión.
54) Al número entero más cercano, ¿cuál es la capacidad de carga prevista del modelo?
- Responder
-
acerca de\(136\)
55) Utilice la función de intersección para encontrar el valor\(x\) para el cual el modelo alcanza la mitad de su capacidad de carga.
Extensiones
56) Recordemos que la forma general de una ecuación logística para una población viene dada por\(P(t)=\dfrac{c}{1+ae^{-bt}}\)
- Contestar
-
Trabajando con el lado izquierdo de la ecuación, vemos que se puede reescribir como\(ae^{-bt}\)
: \ (\ begin {alinear*}
\ dfrac {c-P (t)} {P (t)} &=\ dfrac {c-\ frac {c} {1+ae^ {-bt}}} {\ frac {c} {1+ae^ {-bt}}}\\
&=\ dfrac {\ frac {c\ izquierda (1+ae^ {-bt}\ derecha) -c} {1+ae^ {-bt}}} {\ frac {c} {1+ae^ {-bt}}}\\
&=\ dfrac {\ frac {c\ izquierda (1+ae^ {-bt} -1\ derecha)} {1+ae^ {-bt}}} {\ frac {c} {1+ae^ {-bt}}}\\
&= 1+ae^ {-bt} -1\\
&= ae^ {-bt}
\ end {align*}\)\(\begin{align*} P_0 &= \dfrac{c}{1+ae^{-b(0)}}\\ &= \dfrac{c}{1+a} \end{align*}\)
Por lo tanto,
\ (\ begin {alinear*}
\ dfrac {c-p_0} {P_0} e^ {-bt} &=\ dfrac {c-\ frac {c} {1+a}} {\ frac {c} {1+a}} e^ {-bt}\\
&=\ dfrac {\ frac {c (1+a) -c} {1+a}} {frac {c} {1+a}} e^ {-bt}\\
&=\ dfrac {\ frac {c (1+a -1)} {1+a}} {\ frac {c} {1+a}} e^ {-bt}\\
&= (1+a -1) e^ {-bt}\\
&= ae^ {-bt}
\ end {alinear*}\)Por lo tanto,
\(\dfrac{c-P(t)}{P(t)}=\dfrac{c-P_0}{P_0}e^{-bt}\)
57) Utilice una utilidad gráfica para encontrar una fórmula de regresión exponencial\(f(x)\) y una fórmula de regresión logarítmica\(g(x)\) para los puntos\((1.5,1.5)\) y\((8.5,8.5\)
58) Verificar la conjetura hecha en el ejercicio anterior. Redondear todos los números a seis decimales cuando sea necesario.
- Contestar
-
Primero reescribe el exponencial con base e:\(f(x)=1.034341e^{0.247800x}\)
. , \(\begin{align*} g(f(x)) &= 4.035510\ln\left (1.034341e^{0.247800x}\right )-0.136259\\ &= 4.03551(\ln \left(1.034341)+\ln\left (e^{0.2478x} \right)\right)-0.136259\\ &= 4.03551(\ln(1.034341)+0.2478x)-0.136259\\ &= 0.136257+0.999999x-0.136259\\ &= -0.000002+0.999999x\\ &\approx 0+x \\ &= x \end{align*}\)
59) Encontrar la función inversa\(f^{-1}(x)\) para la función logística\(f(x)=\dfrac{c}{1+ae^{-bx}}\)
60) Utilizar el resultado del ejercicio anterior para graficar el modelo logístico\(P(t)=\dfrac{20}{1+4e^{-0.5t}}\)
- Contestar
-
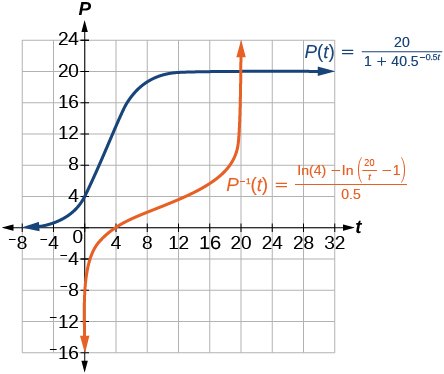
La gráfica de\(P(t)\) tiene una\(y\) intersección en\((0, 4)\) y asíntotas horizontales en\(y = 0\) y\(y = 20\). La gráfica de\(P^{-1}(t)\) tiene una\(x\) - intercepción en\((4, 0)\) y asíntotas verticales en\(x = 0\) y\(x = 20\).


