6.1: Gráficas de las funciones de seno y coseno
- Page ID
- 121318
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
- Variaciones gráficas de\(y=\sin( x )\) y\(y=\cos( x )\).
- Utilice desplazamientos de fase de curvas sinusoidales y cosenales.
La luz blanca, como la luz del sol, en realidad no es blanca en absoluto. En cambio, es una composición de todos los colores del arco iris en forma de ondas. Los colores individuales solo se pueden ver cuando la luz blanca pasa a través de un prisma óptico que separa las ondas según sus longitudes de onda para formar un arco iris.

Las ondas de luz se pueden representar gráficamente por la función sinusoidal. En el capítulo sobre Funciones trigonométricas, examinamos funciones trigonométricas como la función sinusoidal. En esta sección, interpretaremos y crearemos gráficas de funciones sinusoidales y cosenales.
Graficar las funciones de seno y coseno
Recordemos que las funciones seno y coseno relacionan valores de números reales con las\(y\) coordenadas\(x\) - y -de un punto en el círculo unitario. Entonces, ¿cómo se ven en una gráfica en un plano de coordenadas? Empecemos con la función sinusoidal. Podemos crear una tabla de valores y utilizarlos para bosquejar una gráfica. Tabla\(\PageIndex{1}\) enumera algunos de los valores para la función seno en un círculo unitario.
| \(x\) | \(0\) | \(\frac{\pi}{6}\) | \(\frac{\pi}{4}\) | \(\frac{\pi}{3}\) | \(\frac{\pi}{2}\) | \(\dfrac{2\pi}{3}\) | \(\dfrac{3\pi}{4}\) | \(\dfrac{5\pi}{6}\) | \(\pi\) |
|---|---|---|---|---|---|---|---|---|---|
| \(\sin(x)\) | \(0\) | \(\frac{1}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(1\) | \(\dfrac{\sqrt{3}}{2}\) | \(\dfrac{\sqrt{2}}{2}\) | \(\dfrac{1}{2}\) | \(0\) |
Trazar los puntos de la tabla y continuar a lo largo del eje x da la forma de la función sinusoidal. Ver Figura\(\PageIndex{2}\).
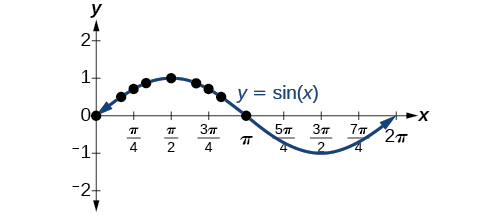
Observe cómo los valores sinusoidales son positivos entre\(0\) y\(\pi\), que corresponden a los valores de la función sinusoidal en los cuadrantes I y II en el círculo unitario, y los valores sinusoidales son negativos entre\(\pi\) y\(2\pi\), que corresponden a los valores de la función sinusoidal en los cuadrantes III y IV en el círculo unitario. Ver Figura\(\PageIndex{3}\).
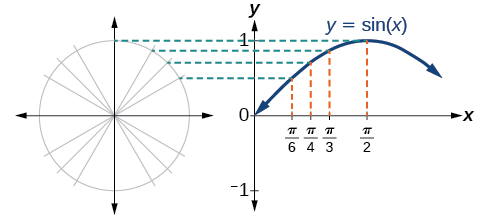
Ahora echemos un vistazo similar a la función coseno. Nuevamente, podemos crear una tabla de valores y utilizarlos para bosquejar una gráfica. Tabla\(\PageIndex{2}\) enumera algunos de los valores para la función coseno en un círculo unitario.
| \(x\) | \(0\) | \(\frac{\pi}{6}\) | \(\frac{\pi}{4}\) | \(\frac{\pi}{3}\) | \(\frac{\pi}{2}\) | \(\frac{2\pi}{3}\) | \(\dfrac{3\pi}{4}\) | \(\dfrac{5\pi}{6}\) | \(\pi\) |
|---|---|---|---|---|---|---|---|---|---|
| \(\cos(x)\) | \(1\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\dfrac{1}{2}\) | \(0\) | \(-\dfrac{1}{2}\) | \(-\dfrac{\sqrt{2}}{2}\) | \(-\dfrac{\sqrt{3}}{2}\) | \(-1\) |
Al igual que con la función seno, podemos trazar puntos para crear una gráfica de la función coseno como en la Figura\(\PageIndex{4}\).
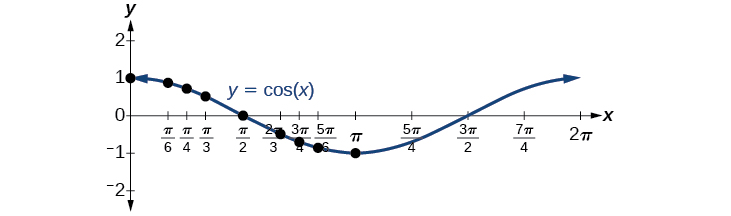
Debido a que podemos evaluar el seno y el coseno de cualquier número real, ambas funciones se definen para todos los números reales. Al pensar en los valores de seno y coseno como coordenadas de puntos en un círculo unitario, queda claro que el rango de ambas funciones debe ser el intervalo\([ −1,1 ]\).
En ambas gráficas, la forma de la gráfica se repite después\(2\pi\), lo que significa que las funciones son periódicas con un periodo de\(2\pi\). Una función periódica es una función para la cual un desplazamiento horizontal específico,\(P\), da como resultado una función igual a la función original:\(f(x+P)=f(x)\) para todos los valores de\(x\) en el dominio de\(f\). Cuando esto ocurre, llamamos al menor desplazamiento horizontal de este tipo con\(P>0\) el periodo de la función. La figura\(\PageIndex{5}\) muestra varios periodos de las funciones seno y coseno.
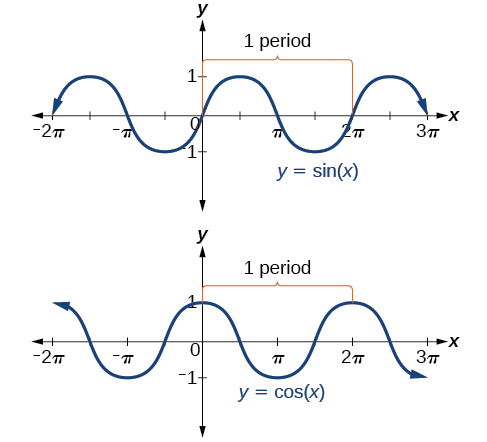
Mirar de nuevo las funciones seno y coseno en un dominio centrado en el\(y\) eje ayuda a revelar simetrías. Como podemos ver en la Figura\(\PageIndex{6}\), la función sinusoidal es simétrica sobre el origen. Recordemos de Las Otras Funciones Trigonométricas que determinamos a partir del círculo unitario que la función sinusoidal es una función impar porque\(\sin(−x)=−\sin\space x\). Ahora podemos ver claramente esta propiedad desde la gráfica.
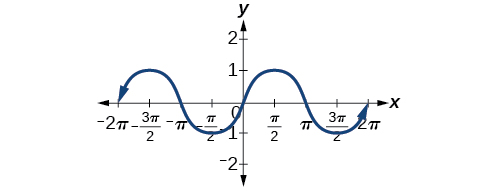
La figura\(\PageIndex{7}\) muestra que la función coseno es simétrica alrededor del\(y\) eje -eje. Nuevamente, determinamos que la función coseno es una función par. Ahora podemos ver por la gráfica que\(\cos(−x)=\cos\space x\).
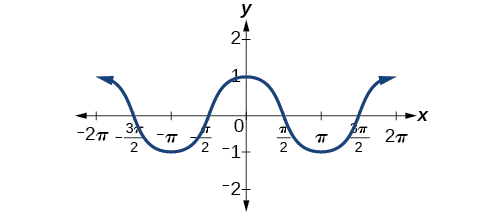
Las funciones seno y coseno tienen varias características distintas:
- Son funciones periódicas con un periodo de\(2\pi\).
- El dominio de cada función es\((−\infty,\infty)\) y el rango es\([ −1,1 ]\).
- La gráfica de\(y=\sin\space x\) es simétrica sobre el origen, porque es una función impar.
- El gráfico de\(y=\cos\space x\) es simétrico alrededor de ellos-\(y\) -eje, porque es una función par.
Investigar funciones sinusoidales
Como podemos ver, las funciones seno y coseno tienen un período y rango regulares. Si observamos olas u ondas oceánicas en un estanque, veremos que se asemejan a las funciones seno o coseno. Sin embargo, no son necesariamente idénticos. Algunos son más altos o más largos que otros. Una función que tiene la misma forma general que una función sinusoidal o coseno se conoce como función sinusoidal. Las formas generales de las funciones sinusoidales son
\[y=A\sin(Bx−C)+D\]
y
\[y=A\cos(Bx−C)+D\]
Determinación del Periodo de Funciones Sinusoidales
Al observar las formas de las funciones sinusoidales, podemos ver que son transformaciones de las funciones sinusoidales y cosenoidales. Podemos usar lo que sabemos de las transformaciones para determinar el periodo.
En la fórmula general,\(B\) se relaciona con el periodo por\(P=\dfrac{2\pi}{|B|}\). Si\(|B|>1\), entonces el periodo es menor que\(2\pi\) y la función sufre una compresión horizontal, mientras que si\(| B |<1\), entonces el periodo es mayor que\(2\pi\) y la función se somete a un estiramiento horizontal. Por ejemplo,\(f(x)=\sin(x)\),\(B=1\), así es el periodo\(2\pi\), que sabíamos. Si\(f(x)=\sin(2x)\), entonces\(B=2\), así es el periodo\(\pi\) y la gráfica se comprime. Si\(f(x)=\sin\left(\dfrac{x}{2}\right)\), entonces\(B=\dfrac{1}{2}\), así es el periodo\(4\pi\) y se estira la gráfica. Observe en la Figura\(\PageIndex{8}\) cómo el periodo se relaciona indirectamente con\(|B|\).
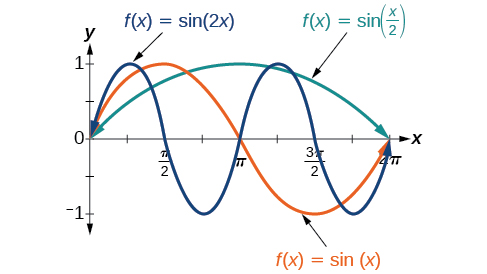
Si dejamos\(C=0\) y\(D=0\) en la forma general ecuaciones de las funciones seno y coseno, obtenemos las formas
- \(y=A\sin(Bx)\)
- \(y=A\cos(Bx)\)
El periodo es\(\dfrac{2\pi}{|B|}\).
Determinar el periodo de la función\(f(x)=\sin\left(\dfrac{\pi}{6}x\right)\).
Solución
Comencemos comparando la ecuación con la forma general\(y=A\sin(Bx)\).
En la ecuación dada,\(B=\dfrac{\pi}{6}\), por lo que el periodo será
\[ \begin{align*} P&=\dfrac{2\pi}{|B|} \\[4pt] &=\dfrac{2\pi}{\dfrac{\pi}{6}} \\ &=2\pi ⋅ \dfrac{6}{\pi} \\[4pt] &=12 \end{align*}\]
Determinar el periodo de la función\(g(x)=\cos(\frac{x}{3})\).
- Responder
-
\(6\pi\)
Determinación de Amplitud
Volviendo a la fórmula general para una función sinusoidal, hemos analizado cómo la variable\(B\) se relaciona con el periodo. Ahora volvamos a la variable para\(A\) que podamos analizar cómo se relaciona con la amplitud, o mayor distancia del descanso. \(A\)representa el factor de estiramiento vertical, y su valor absoluto\(|A|\) es la amplitud. Los máximos locales serán una distancia\(|A|\) por encima de la línea media vertical de la gráfica, que es la línea\(x=D\); porque\(D=0\) en este caso, la línea media es el eje x. Los mínimos locales estarán a la misma distancia por debajo de la línea media. Si\(| A |>1\), la función se estira. Por ejemplo, la amplitud de\(f(x)=4 sin x\) es el doble de la amplitud de
\(f(x)=2\sin x\)
Si\(| A |<1\), la función está comprimida. La figura\(\PageIndex{9}\) compara varias funciones sinusoidales con diferentes amplitudes.
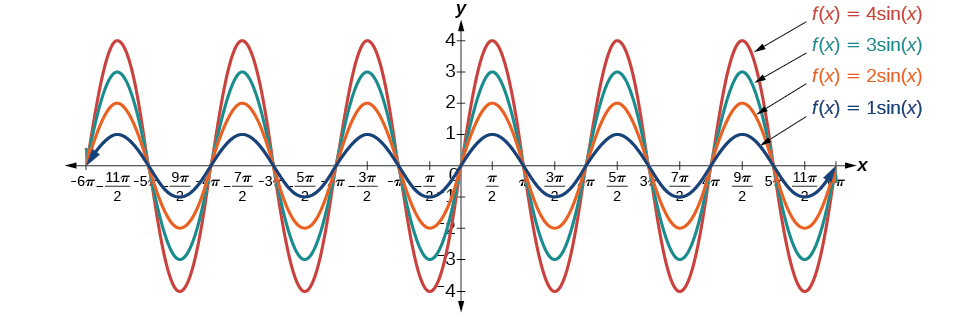
Si dejamos\(C=0\) y\(D=0\) en la forma general ecuaciones de las funciones seno y coseno, obtenemos las formas
\[\begin{align} y=A\sin(Bx)\text { and } y=A\cos(Bx) \end{align}\]
La amplitud es\(A\), y la altura vertical desde la línea media es\(|A|\). Además, observe en el ejemplo que
\[|A| = amplitude = \dfrac{1}{2}∣maximum − minimum|\]
¿Cuál es la amplitud de la función sinusoidal\(f(x)=−4\sin(x)\)? ¿La función se estira o comprime verticalmente?
Solución
Comencemos comparando la función con la forma simplificada\(y=A\sin(Bx)\).
En la función dada,\(A=−4\), así es la amplitud\(| A |=| −4 |=4\). La función se estira.
Análisis
El valor negativo de\(A\) da como resultado una reflexión a través del\(x\) eje -eje de la función sinusoidal, como se muestra en la Figura\(\PageIndex{10}\).
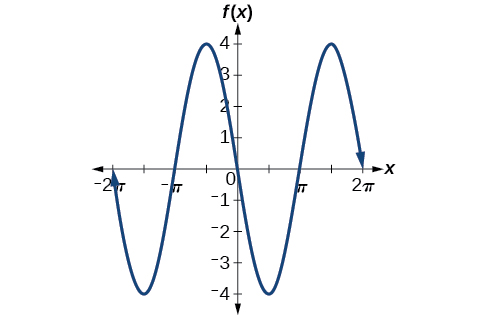
¿Cuál es la amplitud de la función sinusoidal\(f(x)=\frac{1}{2}\sin(x)\)? ¿La función se estira o comprime verticalmente?
- Contestar
-
\(\frac{1}{2}\)comprimido
Análisis de Gráficas de Variaciones de\(y = \sin\space x\) y\(y = \cos\space x\)
Ahora que entendemos cómo\(A\) y nos\(B\) relacionamos con la ecuación general de forma para las funciones seno y coseno, exploraremos las variables\(C\) y\(D\). Recordemos la forma general:
\[y=A\sin(Bx-C)+D\qquad \text{ and } \qquad y=A\cos(Bx-C)+D\]
o
\[y=A\sin\left (B\left (x-\dfrac{C}{B} \right ) \right )+D \qquad \text{ and } \qquad y=A\cos\left (B\left (x-\dfrac{C}{B} \right ) \right )+D\]
El valor\(\frac{C}{B}\) para una función sinusoidal se denomina desplazamiento de fase, o desplazamiento horizontal de la función básica seno o coseno. Si\(C>0\), la gráfica se desplaza hacia la derecha. Si\(C<0\), la gráfica se desplaza hacia la izquierda. Cuanto mayor sea el valor de\(| C |\), más se desplaza la gráfica. La figura\(\PageIndex{11}\) muestra que la gráfica de\(f(x)=\sin(x−\pi)\) desplazamientos hacia la derecha por\(\pi\) unidades, que es más de lo que vemos en la gráfica de\(f(x)=\sin\left(x−\frac{\pi}{4}\right)\), que se desplaza hacia la derecha por\(\frac{\pi}{4}\) unidades.
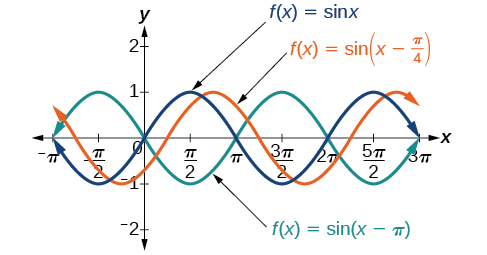
Si bien\(C\) se relaciona con el desplazamiento horizontal,\(D\) indica el desplazamiento vertical desde la línea media en la fórmula general para una función sinusoidal. Ver Figura\(\PageIndex{12}\). La función\(y=\cos(x)+D\) tiene su línea media en\(y=D\).
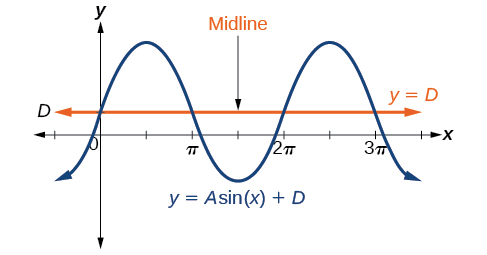
Cualquier valor que no\(D\) sea cero desplaza la gráfica hacia arriba o hacia abajo. La figura\(\PageIndex{13}\) se compara\(f(x)=\sin x\) con\(f(x)=\sin x+2\), que se desplaza\(2\) unidades hacia arriba en una gráfica.
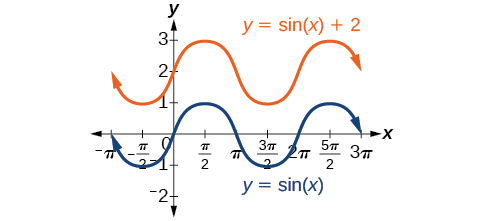
Dada una ecuación en la forma\(f(x)=A \sin (Bx−C)+D\) o\(f(x)=A \cos (Bx−C)+D\),\(\frac{C}{D}\) es el desplazamiento de fase y\(D\) es el desplazamiento vertical.
Determinar la dirección y magnitud del desplazamiento de fase para\(f(x)=\sin\left(x+\frac{\pi}{6}\right)−2\).
Solución
Comencemos comparando la ecuación con la forma general\(y=A\sin(Bx−C)+D\).
En la ecuación dada, observe que\(B=1\) y\(C=−\frac{\pi}{6}\). Entonces el cambio de fase es
\[\begin{align*} \dfrac{C}{B}&= -\frac{\frac{\pi}{6}}{1}\\ &= -\frac{\pi}{6} \end{align*}\]
o\(\frac{\pi}{6}\) unidades a la izquierda.
Análisis
Debemos prestar atención al signo en la ecuación para la forma general de una función sinusoidal. La ecuación muestra un signo menos antes\(C\). Por lo tanto se\(f(x)=\sin(x+\frac{\pi}{6})−2\) puede reescribir como\(f(x)=\sin\left(x−\left(−\frac{\pi}{6}\right)\right)−2\). Si el valor de\(C\) es negativo, el desplazamiento es hacia la izquierda.
Determinar la dirección y magnitud del desplazamiento de fase para\(f(x)=3\cos\left(x−\frac{\pi}{2}\right)\).
- Contestar
-
\(\frac{\pi}{2}\); derecho
Determinar la dirección y magnitud del desplazamiento vertical para\(f(x)=\cos(x)−3\).
Solución
Comencemos comparando la ecuación con la forma general\(y=A\cos(Bx−C)+D\).
En la ecuación dada,\(D=−3\) por lo que el desplazamiento es\(3\) unidades a la baja.
Determinar la dirección y magnitud del desplazamiento vertical para\(f(x)=3\sin(x)+2\).
- Contestar
-
\(2\)unidades arriba
- Determinar la amplitud como\(| A |\).
- Determinar el periodo como\(P=\frac{2\pi}{| B |}\).
- Determinar el desplazamiento de fase como\(\frac{C}{B}\).
- Determinar la línea media como\(y=D\).
Determinar la línea media, amplitud, periodo y desplazamiento de fase de la función\(y=3\sin (2x)+1\).
Solución
Comencemos comparando la ecuación con la forma general\(y=A\sin (Bx−C)+D\).
\(A=3\), entonces la amplitud es\(| A |=3\).
A continuación\(B=2\),, así es el periodo\(P=\dfrac{2\pi}{| B |}=\dfrac{2\pi}{2}=\pi\).
No hay constante agregada dentro de los paréntesis, entonces\(C=0\) y el desplazamiento de fase es\(\dfrac{C}{B}=\dfrac{0}{2}=0\).
Por último\(D=1\),, así es la línea media\(y=1\).
Análisis
Inspeccionando la gráfica, podemos determinar que el periodo es\(\pi\), la línea media es\(y=1\), y la amplitud es\(3\). Ver Figura\(\PageIndex{14}\).
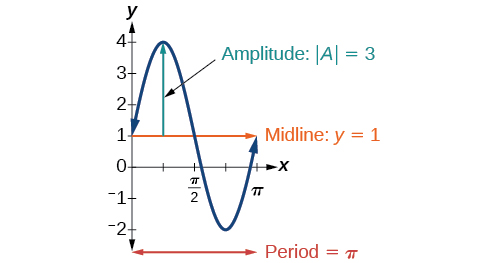
Determinar la línea media, amplitud, periodo y desplazamiento de fase de la función\(y=\frac{1}{2}\cos \left(\frac{x}{3}−\frac{\pi}{3}\right)\).
- Contestar
-
línea media:\(y=0\); amplitud:\(| A |=\frac{1}{2}\); periodo:\(P=\frac{2\pi}{| B |}=6π\); desplazamiento de fase:\(\frac{C}{B}=\pi\)
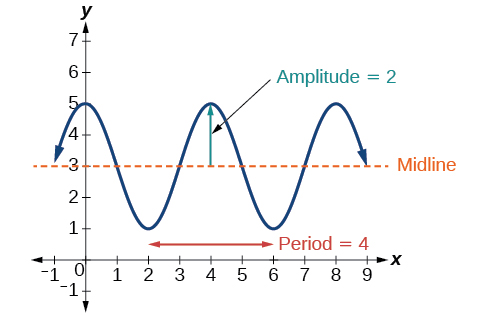
Determinar la fórmula para la función coseno en la Figura\(\PageIndex{15}\).
![Una gráfica de -0.5cos (x) +0.5. La gráfica tiene una amplitud de 0.5. La gráfica tiene un periodo de 2pi. La gráfica tiene un rango de [0, 1]. La gráfica también se refleja sobre el eje x desde la función principal cos (x).](https://math.libretexts.org/@api/deki/files/6903/CNX_Precalc_Figure_06_01_015.jpg)
Solución
Para determinar la ecuación, necesitamos identificar cada valor en la forma general de una función sinusoidal.
\(y=A\sin (Bx−C)+D\)
\(y=A\cos (Bx−C)+D\)
La gráfica podría representar una función sinusoidal o coseno que se desplaza y/o refleja. Cuando\(x=0\), la gráfica tiene un punto extremo,\((0,0)\). Dado que la función coseno tiene un punto extremo para\(x=0\), escribamos nuestra ecuación en términos de una función coseno.
Empecemos por la línea media. Podemos ver que la gráfica sube y baja a igual distancia arriba y abajo\(y=0.5\). Este valor, que es la línea media, está\(D\) en la ecuación, entonces\(D=0.5\).
La mayor distancia por encima y por debajo de la línea media es la amplitud. Los máximos son\(0.5\) unidades por encima de la línea media y los mínimos son\(0.5\) unidades por debajo de la línea media. Entonces\(| A |=0.5\). Otra forma en que podríamos haber determinado la amplitud es reconociendo que la diferencia entre la altura de máximos y mínimos locales es\(1\), así\(| A |=\frac{1}{2}=0.5\). Además, la gráfica se refleja alrededor del\(x\) eje -para que\(A=−0.5\).
La gráfica no está estirada o comprimida horizontalmente, por lo que\(B=1\); y la gráfica no se desplaza horizontalmente, entonces\(C=0\).
Poniendo todo esto junto,
\(g(x)=−0.5\cos (x)+0.5\)
Determinar la fórmula para la función sinusoidal en la Figura\(\PageIndex{16}\).
![Una gráfica de pecado (x) +2. Periodo de 2pi, amplitud de 1 y rango de [1, 3].](https://math.libretexts.org/@api/deki/files/6904/CNX_Precalc_Figure_06_01_016.jpg)
- Contestar
-
\(f(x)=\sin(x)+2\)
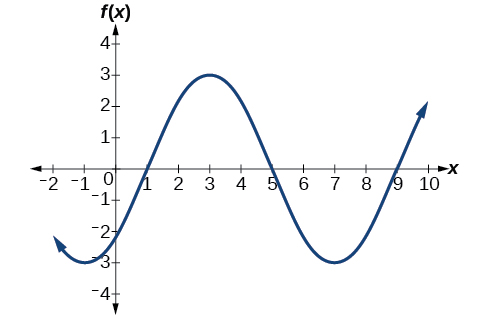
Determinar la ecuación para la función sinusoidal en la Figura\(\PageIndex{17}\).
![Una gráfica de 3cos (pi/3x-pi/3) -2. La gráfica tiene amplitud de 3, periodo de 6, rango de [-5,1].](https://math.libretexts.org/@api/deki/files/6905/CNX_Precalc_Figure_06_01_017.jpg)
Solución
Con el valor más alto en\(1\) y el valor más bajo en\(−5\), la línea media estará a medio camino entre at\(−2\). Entonces\(D=−2\).
La distancia desde la línea media hasta el valor más alto o más bajo da una amplitud de\(| A |=3\).
El periodo de la gráfica es\(6\), que se puede medir desde el pico en\(x=1\) hasta el siguiente pico en\(x=7\), o desde la distancia entre los puntos más bajos. Por lo tanto,\(P=\dfrac{2\pi}{| B |}=6\). Usando el valor positivo para\(B\), encontramos que
\[\begin{align*} B&=\dfrac{2\pi}{P}\\ &=\dfrac{2\pi}{6}\\ &=\dfrac{\pi}{3} \end{align*}\]
Hasta el momento, nuestra ecuación es\(y=3\sin\left(\dfrac{\pi}{3}x−C\right)−2\) o bien\(y=3\cos\left(\dfrac{\pi}{3}x−C\right)−2\). Para la forma y el cambio, tenemos más de una opción. Podríamos escribir esto como cualquiera de los siguientes:
- un coseno desplazado hacia la derecha
- un coseno negativo desplazado hacia la izquierda
- un seno desplazado hacia la izquierda
- un seno negativo desplazado hacia la derecha
Si bien cualquiera de estos sería correcto, los desplazamientos coseno son más fáciles de trabajar que los cambios sinusoidales en este caso porque involucran valores enteros. Entonces nuestra función se convierte
\[\begin{align*} y&=3\cos \left (\frac{\pi}{3}x-\dfrac{\pi}{3} \right )-2 \qquad \text{or} \\ y&=-3\cos \left (\dfrac{\pi}{3}x+\dfrac{2\pi}{3} \right )-2 \end{align*}\]
Nuevamente, estas funciones son equivalentes, por lo que ambas producen la misma gráfica.
Escribe una fórmula para la función graficada en la Figura\(\PageIndex{18}\).
![Una gráfica de 4sin ((pi/5) x-pi/5) +4. La gráfica tiene periodo de 10, amplitud de 4, rango de [0,8].](https://math.libretexts.org/@api/deki/files/6906/CNX_Precalc_Figure_06_01_018n.jpg)
- Contestar
-
dos posibilidades:\(y=4\sin\left(\dfrac{\pi}{5}x−\dfrac{\pi}{5}\right)+4\) o\(y=−4\sin\left(\dfrac{\pi}{5}x+\dfrac{4\pi}{5}\right)+4\)
Graficando variaciones de\(y = \sin\space x\) y\(y = \cos\space x\)
A lo largo de esta sección, hemos aprendido sobre los tipos de variaciones de las funciones sinusoidales y cosenales y hemos utilizado esa información para escribir ecuaciones a partir de gráficas. Ahora podemos usar la misma información para crear gráficas a partir de ecuaciones.
En lugar de centrarse en las ecuaciones generales de forma
\(y=A\sin(Bx-C)+D \text{ and } y=A\cos(Bx-C)+D\)
vamos a dejar\(C=0\) y\(D=0\) y trabajar con una forma simplificada de las ecuaciones en los siguientes ejemplos.
- Identificar la amplitud,\(| A |\).
- Identificar el periodo,\(P=\dfrac{2\pi}{| B |}\).
- Empezar en el origen, con la función aumentando a la derecha si\(A\) es positiva o decreciente si\(A\) es negativa.
- En\(x=\dfrac{\pi}{2| B |}\) hay un máximo local para\(A>0\) o un mínimo para\(A<0\), con\(y=A\).
- La curva vuelve al eje x en\(x=\dfrac{\pi}{| B |}\).
- Hay un mínimo local para\(A>0\) (máximo para\(A<0\)) en\(x=\dfrac{3\pi}{2| B |}\) con\(y=–A\).
- La curva vuelve nuevamente al eje x en\(x=\dfrac{\pi}{2| B |}\).
Esbozar una gráfica de\(f(x)=−2\sin\left(\dfrac{\pi x}{2}\right)\).
Solución
Comencemos comparando la ecuación con la forma\(y=A\sin(Bx)\).
- Paso 1. Podemos ver a partir de la ecuación que\(A=−2\), por lo que la amplitud es 2.
\(|A|=2 \)
- Paso 2. La ecuación muestra que\(B=\dfrac{\pi}{2}\), por lo que el periodo es
\[\begin{align*} P&=\dfrac{2\pi}{\dfrac{\pi}{2}}\\ &=2\pi \cdot \dfrac{2}{\pi}\\ &=4 \end{align*}\]
- Paso 3. Porque\(A\) es negativo, la gráfica desciende a medida que nos movemos hacia la derecha del origen.
- Paso 4. Los\(x\) -interceptos son al inicio de un periodo,\(x=0\), los puntos medios horizontales están en\(x=2\) y al final de un periodo en\(x=4\).
Los puntos trimestrales incluyen el mínimo en\(x=1\) y el máximo en\(x=3\). Un mínimo local ocurrirá\(2\) unidades por debajo de la línea media, en\(x=1\), y un máximo local ocurrirá en\(2\) unidades por encima de la línea media, en\(x=3\). La figura\(\PageIndex{19}\) muestra la gráfica de la función.
![Una gráfica de -2sin ((pi/2) x). La gráfica tiene rango de [-2,2], periodo de 4 y amplitud de 2.](https://math.libretexts.org/@api/deki/files/6907/CNX_Precalc_Figure_06_01_019.jpg)
Esbozar una gráfica de\( g(x)=−0.8\cos(2x)\). Determinar la línea media, amplitud, periodo y desplazamiento de fase.
- Contestar
-
![Una gráfica de -0.8cos (2x). La gráfica tiene rango de [-0.8, 0.8], periodo de pi, amplitud de 0.8, y se refleja alrededor del eje x en comparación con su función padre cos (x).](https://math.libretexts.org/@api/deki/files/6908/CNX_Precalc_Figure_06_01_020.jpg)
Figura\(\PageIndex{20}\) línea media:\(y=0\); amplitud:\(| A |=0.8\); periodo:\(P=\dfrac{2\pi}{| B |}=\pi\); desplazamiento de fase:\(\dfrac{C}{B}=0\) o ninguno
- Expresar la función en la forma general\(y=A\sin(Bx−C)+D\) o\(y=A\cos(Bx−C)+D\).
- Identificar la amplitud,\(| A |\).
- Identificar el periodo,\(P=\dfrac{2\pi}{| B |}\).
- Identificar el desplazamiento de fase,\(\dfrac{C}{B}\).
- Dibuja la gráfica de\(f(x)=A\sin(Bx)\) desplazado a la derecha o izquierda por\(\dfrac{C}{B}\) y hacia arriba o hacia abajo por\(D\).
Esbozar una gráfica de\(f(x)=3\sin\left(\dfrac{\pi}{4x}−\dfrac{\pi}{4}\right)\).
Solución
- Paso 1. La función ya está escrita en forma general:\(f(x)=3\sin\left(\dfrac{\pi}{4x}−\dfrac{\pi}{4}\right)\) Esta gráfica tendrá la forma de una función sinusoidal, comenzando en la línea media y aumentando hacia la derecha.
- Paso 2. \(| A |=| 3 |=3\). La amplitud es\(3\).
- Paso 3. Ya que\(| B |=| \dfrac{\pi}{4} |=\dfrac{\pi}{4}\), determinamos el periodo de la siguiente manera.
\[\begin{align*} P&=\dfrac{2\pi}{|B|}\\ &=\dfrac{2\pi}{\dfrac{\pi}{4}}\\ &=2\pi \cdot \dfrac{4}{\pi}\\ &=8 \end{align*}\]
El periodo es\(8\).
- Paso 4. Ya que\(C=\dfrac{\pi}{4}\), el desplazamiento de fase es
\[\dfrac{C}{B}=\dfrac{\dfrac{\pi}{4}}{\dfrac{\pi}{4}}=1\].
El desplazamiento de fase es\(1\) unidad.
- Paso 5. La figura\(\PageIndex{21}\) muestra la gráfica de la función.
Dibuja una gráfica de\(g(x)=−2\cos\left(\dfrac{\pi}{3}x+\dfrac{\pi}{6}\right)\). Determinar la línea media, amplitud, periodo y desplazamiento de fase.
- Contestar
-
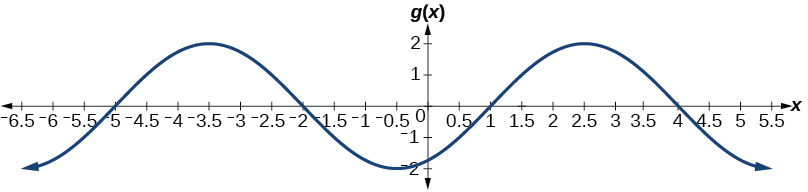
Figura\(\PageIndex{22}\) línea media:\(y=0\); amplitud:\(| A |=2\); periodo:\(P=\dfrac{2\pi}{| B |}=6\); desplazamiento de fase:\(\dfrac{C}{B}=−\dfrac{1}{2}\)
Dado\(y=−2cos\left(\dfrac{\pi}{2}x+\pi\right)+3\), determinar la amplitud, periodo, desplazamiento de fase y desplazamiento horizontal. Después grafica la función.
Solución
Comience comparando la ecuación con la forma general.
\(y=A\cos(Bx−C)+D\)
- Paso 1. La función ya está escrita en forma general.
- Paso 2. Ya que\(A=−2\), la amplitud es\(| A |=2\).
- Paso 3. \(| B |=\dfrac{\pi}{2}\), así es el periodo\(P=\dfrac{2\pi}{| B |}=\dfrac{2\pi}{\dfrac{pi}{2}}=2\pi⋅\dfrac{2}{\pi}=4\). El periodo es 4.
- Paso 4. \(C=−\pi\), por lo que calculamos el desplazamiento de fase como\(\dfrac{C}{B}=−\dfrac{\pi}{\dfrac{\pi}{2}}=−\pi⋅\dfrac{2}{\pi}=−2\). El desplazamiento de fase es\(−2\).
- Paso 5. \(D=3\), entonces la línea media es\(y=3\), y el desplazamiento vertical es hacia arriba\(3\).
Dado que\(A\) es negativo, la gráfica de la función coseno se ha reflejado alrededor del\(x\) eje -eje.
La figura\(\PageIndex{23}\) muestra un ciclo de la gráfica de la función.
Uso de transformaciones de funciones de seno y coseno
Podemos utilizar las transformaciones de las funciones sinusoidales y cosenales en numerosas aplicaciones. Como se mencionó al inicio del capítulo, el movimiento circular se puede modelar usando la función seno o coseno.
Un punto gira alrededor de un círculo de radio\(3\) centrado en el origen. Esboce una gráfica de la\(y\) coordenada -del punto en función del ángulo de rotación.
Solución
Recordemos que, para un punto en un círculo de radio\(r\), la\(y\) coordenada -del punto es\(y=r \sin(x)\), así que en este caso, obtenemos la ecuación\(y(x)=3 \sin(x)\). La constante\(3\) provoca un estiramiento vertical de los\(y\) -valores de la función por un factor de\(3\), que podemos ver en la gráfica de la Figura\(\PageIndex{24}\).
![Una gráfica de 3sin (x). La gráfica tiene periodo de 2pi, amplitud de 3 y rango de [-3,3].](https://math.libretexts.org/@api/deki/files/6912/CNX_Precalc_Figure_06_01_023.jpg)
Análisis
Observe que el periodo de la función está quieto\(2\pi\); a medida que viajamos alrededor del círculo, volvemos al punto\((3,0)\) para\(x=2\pi,4\pi,6\pi,\)... Porque las salidas de la gráfica oscilarán ahora entre\(–3\) y\(3\), la amplitud de la onda sinusoidal es\(3\).
¿Cuál es la amplitud de la función\(f(x)=7\cos(x)\)? Esboce una gráfica de esta función.
- Contestar
-
![Una gráfica de 7cos (x). La gráfica tiene amplitud de 7, periodo de 2pi y rango de [-7,7].](https://math.libretexts.org/@api/deki/files/6913/CNX_Precalc_Figure_06_01_024.jpg)
Figura\(\PageIndex{25}\)
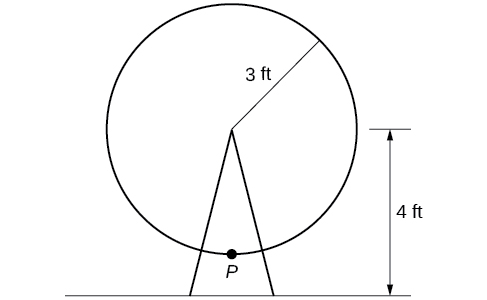
Un círculo con radio\(3\) ft se monta con su\(4\) pie central fuera del suelo. El punto más cercano al suelo está etiquetado\(P\), como se muestra en la Figura\(\PageIndex{26}\). Esboza una gráfica de la altura sobre el suelo del punto a\(P\) medida que se gira el círculo; luego encuentra una función que dé la altura en términos del ángulo de rotación.
Solución
Al esbozar la altura, observamos que comenzará\(1\) pies sobre el suelo, luego aumentará hasta\(7\) pies sobre el suelo, y continuará oscilando\(3\) pies por encima y por debajo del valor central de\(4\) ft, como se muestra en la Figura\(\PageIndex{27}\).
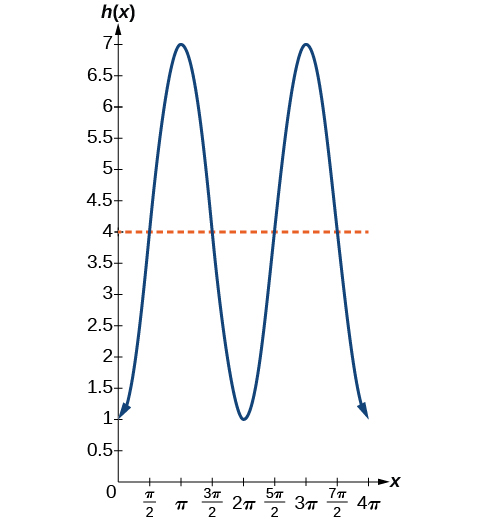
Aunque podríamos usar una transformación de la función sinusoidal o coseno, comenzamos por buscar características que hagan que una función sea más fácil de usar que la otra. Usemos una función coseno porque comienza en el valor más alto o más bajo, mientras que una función sinusoidal comienza en el valor medio. Un coseno estándar comienza en el valor más alto, y esta gráfica comienza en el valor más bajo, por lo que necesitamos incorporar una reflexión vertical.
Segundo, vemos que la gráfica oscila\(3\) por encima y por debajo del centro, mientras que un coseno básico tiene una amplitud de\(1\), por lo que esta gráfica ha sido estirada verticalmente por\(3\), como en el último ejemplo.
Finalmente, para mover el centro del círculo hasta una altura de\(4\), la gráfica ha sido desplazada verticalmente hacia arriba por\(4\). Armando estas transformaciones, encontramos que
\(y=−3\cos(x)+4\)
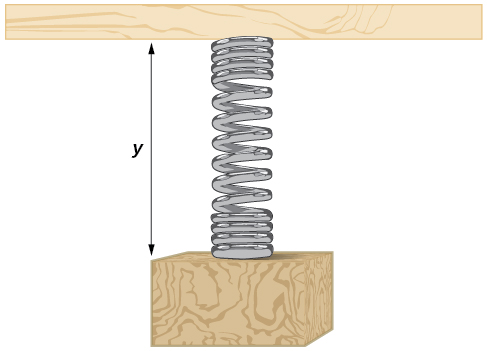
Se fija un peso a un resorte que luego se cuelga de una tabla, como se muestra en la Figura\(\PageIndex{28}\). A medida que el resorte oscila hacia arriba y hacia abajo, la posición\(y\) del peso con respecto a la placa varía desde\(–1\) adentro. (en el momento\(x=0\)) a\(–7\) en. (en el momento\(x=π\)) debajo del tablero. Asumir la posición de\(y\) se da como una función sinusoidal de\(x\). Esbozar una gráfica de la función, y luego encontrar una función coseno que da la posición\(y\) en términos de\(x\).
- Contestar
-
\(y=3\cos(x)−4\)
![Una gráfica coseno con rango [-1, -7]. El periodo es de 2 pi. Máximo local en (0, -1), (2pi, -1) y (4pi, -1). Mínimos locales en (pi, -7) y (3pi, -7).](https://math.libretexts.org/@api/deki/files/6917/CNX_Precalc_Figure_06_01_027.jpg)
Figura\(\PageIndex{29}\)
El London Eye es una enorme noria con un diámetro de\(135\) metros (\(443\)pies). Completa una rotación cada\(30\) minuto. Los jinetes suben desde una plataforma\(2\) a metros sobre el suelo. Exprese la altura de un ciclista sobre el suelo en función del tiempo en minutos.
Solución
Con un diámetro de\(135\) m, la rueda tiene un radio de\(67.5\) m. La altura oscilará con amplitud\(67.5\) m por encima y por debajo del centro.
Los pasajeros abordan\(2\) m sobre el nivel del suelo, por lo que el centro de la rueda debe estar ubicado\(67.5+2=69.5\) m sobre el nivel del suelo. La línea media de la oscilación estará en\(69.5\) m.
La rueda tarda\(30\) minutos en completar\(1\) la revolución, por lo que la altura oscilará con un periodo de\(30\) minutos.
Por último, debido a que el piloto sube en el punto más bajo, la altura comenzará en el valor más pequeño y aumentará, siguiendo la forma de una curva coseno reflejada verticalmente.
- Amplitud:\(67.5\), entonces\(A=67.5\)
- Línea media:\(69.5\), entonces\(D=69.5\)
- Periodo:\(30\), entonces\(B=\dfrac{2\pi}{30}=\dfrac{\pi}{15}\)
- Forma:\(−\cos(t)\)
Una ecuación para la altura del piloto sería
\(y=−67.5\cos\left(\dfrac{\pi}{15}t\right)+69.5\)
donde\(t\) está en minutos y\(y\) se mide en metros.
Acceda a estos recursos en línea para obtener instrucción y práctica adicionales con gráficas de funciones sinusoidales y cosenales.
- Amplitud y Periodo de Seno y Coseno
- Traducciones de Sine and Cosine
- Graficando las transformaciones de seno y coseno
- Graficando la función sinusoidal
Ecuaciones Clave
| Funciones sinusoidales |
\(f(x)=A\sin(Bx−C)+D\) \(f(x)=A\cos(Bx−C)+D\) |
Conceptos clave
- Las funciones periódicas se repiten después de un valor dado. El menor valor de este tipo es el periodo. Las funciones básicas seno y coseno tienen un período de\(2\pi\).
- La función\(\sin x\) es impar, por lo que su gráfica es simétrica sobre el origen. La función\(\cos x\) es pareja, por lo que su gráfica es simétrica alrededor del eje y.
- El gráfico de una función sinusoidal tiene la misma forma general que una función sinusoidal o coseno.
- En la fórmula general para una función sinusoidal, el periodo es\(P=\dfrac{2\pi}{| B |}\). Ver Ejemplo\(\PageIndex{1}\).
- En la fórmula general para una función sinusoidal,\( | A |\) representa amplitud. Si\(| A |>1\), la función se estira, mientras que if\(| A |<1\), la función se comprime. Ver Ejemplo\(\PageIndex{2}\).
- El valor\(\dfrac{C}{B}\) en la fórmula general para una función sinusoidal indica el desplazamiento de fase. Ver Ejemplo\(\PageIndex{3}\).
- El valor\(D\) en la fórmula general para una función sinusoidal indica el desplazamiento vertical desde la línea media. Ver Ejemplo\(\PageIndex{4}\).
- Se pueden detectar combinaciones de variaciones de funciones sinusoidales a partir de una ecuación. Ver Ejemplo\(\PageIndex{5}\).
- La ecuación para una función sinusoidal se puede determinar a partir de una gráfica. Ver Ejemplo\(\PageIndex{6}\) y Ejemplo\(\PageIndex{7}\).
- Una función se puede graficar identificando su amplitud y periodo. Ver Ejemplo\(\PageIndex{8}\) y Ejemplo\(\PageIndex{9}\).
- Una función también se puede graficar identificando su amplitud, periodo, desplazamiento de fase y desplazamiento horizontal. Ver Ejemplo\(\PageIndex{10}\).
- Las funciones sinusoidales se pueden utilizar para resolver problemas del mundo real. Ver Ejemplo\(\PageIndex{11}\)\(\PageIndex{12}\), Ejemplo y Ejemplo\(\PageIndex{13}\).


