6.2: Gráficas de las Otras Funciones Trigonométricas

Objetivos de aprendizaje

• Analizar la gráfica de\(y=\tan x\).
• Gráfica variaciones de\(y=\tan x\).
• Analizar las gráficas de\(y=\sec x\) y\(y=\csc x\).
• Variaciones gráficas de\(y=\sec x\) y\(y=\csc x\).
• Analizar la gráfica de\(y=\cot x\).
• Gráfica variaciones de\(y=\cot x\).

Sabemos que la función tangente se puede utilizar para encontrar distancias, como la altura de un edificio, montaña o asta de bandera. Pero, ¿y si queremos medir ocurrencias repetidas de distancia? Imagínese, por ejemplo, un carro de policía estacionado junto a un almacén. La luz giratoria del carro de policía viajaría a través de la pared del almacén en intervalos regulares. Si la entrada es tiempo, la salida sería la distancia que recorre el haz de luz. El haz de luz repetiría la distancia a intervalos regulares. La función tangente se puede utilizar para aproximar esta distancia. Se necesitarían asíntotas para ilustrar los ciclos repetidos cuando el haz discurre paralelo a la pared porque, aparentemente, el haz de luz podría parecer extenderse para siempre. La gráfica de la función tangente ilustraría claramente los intervalos repetidos. En esta sección, exploraremos las gráficas de la tangente y otras funciones trigonométricas.

Analizando la Gráfica de\(y =\tan x\)

Comenzaremos con la gráfica de la función tangente, trazando puntos como hicimos para las funciones seno y coseno. Recordemos que

\[\tan \, x=\dfrac{\sin \, x}{\cos \, x}\]

El periodo de la función tangente se\(\pi\) debe a que la gráfica se repite a intervalos de\(k\pi\) donde\(k\) es una constante. Si graficamos la función tangente en\(−\frac{\pi}{2}\) to\(\frac{\pi}{2}\), podemos ver el comportamiento de la gráfica en un ciclo completo. Si nos fijamos en algún intervalo mayor, veremos que las características de la gráfica se repiten.

Podemos determinar si tangente es una función impar o par usando la definición de tangente.

\[\begin{align*} \tan(-x)&= \dfrac{\sin(-x)}{\cos(-x)} \qquad \text{Definition of tangent}\\ &= \dfrac{-\sin \, x}{\cos \, x} \qquad \text{Sine is an odd function, cosine is even}\\ &= -\dfrac{\sin \, x}{\cos \, x} \qquad \text{The quotient of an odd and an even function is odd}\\ &= -\tan \, x \qquad \text{Definition of tangent} \end{align*}\]

Por lo tanto, tangente es una función impar. Podemos analizar más a fondo el comportamiento gráfico de la función tangente observando los valores para algunos de los ángulos especiales, como se indica en Tabla\(\PageIndex{1}\).

Mesa\(\PageIndex{1}\)

\(x\)	\(−\dfrac{\pi}{2}\)	\(−\dfrac{\pi}{3}\)	\(−\dfrac{\pi}{4}\)	\(−\dfrac{\pi}{6}\)	0	\(\dfrac{\pi}{6}\)	\(\dfrac{\pi}{4}\)	\(\dfrac{\pi}{3}\)	\(\dfrac{\pi}{2}\)
\(\tan x\)	undefined	\(-\sqrt{3}\)	\(–1\)	\(-\dfrac{\sqrt{3}}{3}\)	0	\(\dfrac{\sqrt{3}}{3}\)	1	\(\sqrt{3}\)	undefined

Estos puntos nos ayudarán a dibujar nuestra gráfica, pero necesitamos determinar cómo se comporta la gráfica donde está indefinida. Si miramos más de cerca los valores cuando\(\frac{\pi}{3}<x<\frac{\pi}{2}\), podemos usar una tabla para buscar una tendencia. Porque\(\frac{\pi}{3}≈1.05\) y\(\frac{\pi}{2}≈1.57\), evaluaremos\(x\) en medidas de radián\(1.05<x<1.57\) como se muestra en la Tabla\(\PageIndex{2}\).

Mesa\(\PageIndex{2}\)

\(x\)	1.3	1.5	1.55	1.56
\(\tan x\)	3.6	14.1	48.1	92.6

A medida que\(x\) se aproxima\(\dfrac{\pi}{2}\), las salidas de la función se hacen cada vez más grandes. Debido a que\(y=\tan \, x\) es una función impar, vemos la tabla correspondiente de valores negativos en Table\(\PageIndex{3}\).

Mesa\(\PageIndex{3}\)

\(x\)	−1.3	−1.5	−1.55	−1.56
\(\tan x\)	−3.6	−14.1	−48.1	−92.6

Podemos ver que, a medida que se\(x\) aproxima\(−\frac{\pi}{2}\), las salidas se hacen cada vez más pequeñas. Recuerda que hay algunos valores de\(x\) para los cuales\(\cos \, x=0\). Por ejemplo,\(\cos \left (\frac{\pi}{2} \right)=0\) y\(\cos \left (\frac{3\pi}{2} \right )=0\). En estos valores, la función tangente es indefinida, por lo que la gráfica de\(y=\tan \, x\) tiene discontinuidades en\(x=\frac{\pi}{2}\) y\(\frac{3\pi}{2}\). A estos valores, la gráfica de la tangente tiene asíntotas verticales. La figura\(\PageIndex{1}\) representa la gráfica de\(y=\tan \, x\). La tangente es positiva desde\(\frac{\pi}{2}\) y\(0\)\(\pi\) hacia\(\frac{3\pi}{2}\), correspondiente a los cuadrantes I y III del círculo unitario.

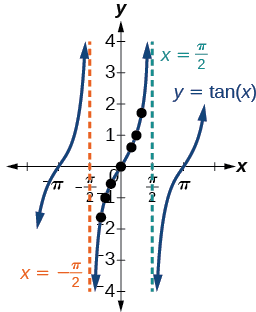
Figura\(\PageIndex{1}\): Gráfica de la función tangente

Graficando variaciones de\(y = \tan \, x\)

Al igual que con las funciones seno y coseno, la función tangente puede describirse mediante una ecuación general.

\[y=A\tan(Bx) \nonumber\]

Podemos identificar estiramientos y compresiones horizontales y verticales utilizando valores de\(A\) y\(B\). El estiramiento horizontal normalmente se puede determinar a partir del periodo de la gráfica. Con las gráficas tangentes, a menudo es necesario determinar un estiramiento vertical usando un punto en la gráfica.

Debido a que no hay valores máximos o mínimos de una función tangente, el término amplitud no puede interpretarse como es para las funciones seno y coseno. En su lugar, usaremos la frase factor de estiramiento/compresión cuando nos referimos a la constante\(A\).

CARACTERÍSTICAS DEL GRAFO\(Y = A \tan(Bx)\)

• El factor de estiramiento es\(|A|\).
• El periodo es\(P=\dfrac{\pi}{|B|}\).
• El dominio es todo números reales\(x\), donde\(x≠\dfrac{\pi}{2| B |}+\dfrac{π}{| B |}k\) tal que\(k\) es un entero.
• El rango es\((−\infty,\infty)\).
• Las asíntotas ocurren en\(x=\dfrac{\pi}{2| B |}+\dfrac{π}{| B |}k\) donde\(k\) es un número entero.
• \(y=A\tan(Bx)\)es una función impar.

Graficar un periodo de una función tangente estirada o comprimida

Podemos usar lo que sabemos sobre las propiedades de la función tangente para esbozar rápidamente una gráfica de cualquier función tangente estirada y/o comprimida de la forma\(f(x)=A\tan(Bx)\). Nos enfocamos en un solo período de la función incluyendo el origen, porque la propiedad periódica nos permite extender la gráfica al resto del dominio de la función si así lo deseamos. Nuestro dominio limitado es entonces el intervalo\(\left (−\dfrac{P}{2},\dfrac{P}{2} \right )\) y la gráfica tiene asíntotas verticales en\(\pm \dfrac{P}{2}\) donde\(P=\dfrac{\pi}{B}\). En\(\left (−\dfrac{\pi}{2},\dfrac{\pi}{2} \right )\), la gráfica saldrá de la asíntota izquierda en\(x=−\dfrac{\pi}{2}\), cruzará por el origen, y continuará aumentando a medida que se acerca a la asíntota derecha en\(x=\dfrac{\pi}{2}\). Para que la función se acerque a las asíntotas a la velocidad correcta, también necesitamos establecer la escala vertical evaluando realmente la función para al menos un punto por el que pasará la gráfica. Por ejemplo, podemos usar

\[f \left (\dfrac{P}{4} \right )=A\tan \left (B\dfrac{P}{4} \right )=A\tan \left (B\dfrac{\pi}{4B} \right )=A \nonumber\]

porque\(\tan \left (\dfrac{\pi}{4} \right )=1\).

Cómo: Dada la función\(f(x)=A \tan(Bx)\), graph one period.

1. Identificar el factor de estiramiento,\(| A |\).
2. Identificar B y determinar el periodo,\(P=\dfrac{\pi}{| B |}\).
3. Dibuja asíntotas verticales en\(x=−\dfrac{P}{2}\) y\(x=\dfrac{P}{2}\).
4. Para\(A>0\), la gráfica se acerca a la asíntota izquierda en valores de salida negativos y a la asíntota derecha en valores de salida positivos (inversa para\(A<0\)).
5. Trazar puntos de referencia en\(\left (\dfrac{P}{4},A \right )\)\((0,0)\), y\(\left (−\dfrac{P}{4},−A \right )\), y dibuje la gráfica a través de estos puntos.

Ejemplo\(\PageIndex{1}\): Sketching a Compressed Tangent

Esbozar una gráfica de un periodo de la función\(y=0.5\tan \left (\dfrac{\pi}{2}x \right )\).

Solución

Primero, identificamos\(A\) y\(B\).

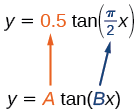
Figura\(\PageIndex{2}\)

Porque\(A=0.5\) y\(B=\dfrac{\pi}{2}\), podemos encontrar el factor de estiramiento/compresión y periodo. El periodo es\(\dfrac{\pi}{\dfrac{\pi}{2}}=2\), por lo que las asíntotas están en\(x=±1\). A un cuarto de periodo desde el origen, tenemos

\[\begin{align*} f(0.5)&= 0.5\tan \left (\dfrac{0.5\pi}{2} \right )\\ &= 0.5\tan \left (\dfrac{\pi}{4} \right )\\ &= 0.5 \end{align*}\]

Esto significa que la curva debe pasar por los puntos\((0.5,0.5)\),\((0,0)\), y\((−0.5,−0.5)\). El único punto de inflexión está en el origen. La figura\(\PageIndex{3}\) muestra la gráfica de un periodo de la función.

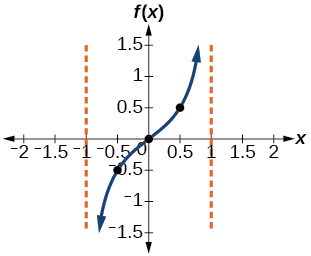
Figura\(\PageIndex{3}\)

Ejercicio\(\PageIndex{1}\)

Esbozar una gráfica de\(f(x)=3\tan \left (\dfrac{\pi}{6}x \right )\).

Contestar

Figura\(\PageIndex{4}\)

Graficar un periodo de una función de tangente desplazada

Ahora que podemos graficar una función tangente que se estira o comprime, agregaremos un desplazamiento vertical y/u horizontal (o de fase). En este caso, agregamos\(C\) y\(D\) a la forma general de la función tangente.

\[f(x)=A\tan(Bx−C)+D \nonumber\]

La gráfica de una función tangente transformada es diferente de la función tangente básica\(\tan x\) de varias maneras:

CARACTERÍSTICAS DEL GRAFO\(Y = A\tan(Bx−C)+D\)

• El factor de estiramiento es\(| A |\).
• El periodo es\(\dfrac{\pi}{| B |}\).
• El dominio es\(x≠\dfrac{C}{B}+\dfrac{\pi}{| B |}k\), donde\(k\) es un entero.
• El rango es\((−∞,−| A |]∪[| A |,∞)\).
• Las asíntotas verticales ocurren en\(x=\dfrac{C}{B}+\dfrac{\pi}{| B |}k\), donde\(k\) es un entero impar.
• No hay amplitud.
• \(y=A \tan(Bx)\)es y función impar porque es la cantidad de funciones pares e impares (pecado y coseno en perspectiva).

Cómo: Dada la función\(y=A\tan(Bx−C)+D\), sketch the graph of one period.

1. Expresar la función dada en el formulario\(y=A\tan(Bx−C)+D\).
2. Identificar el factor de estiramiento/compresión,\(| A |\).
3. Identificar\(B\) y determinar el periodo,\(P=\dfrac{\pi}{|B|}\).
4. Identificar\(C\) y determinar el desplazamiento de fase,\(\dfrac{C}{B}\).
5. Dibuja la gráfica de\(y=A\tan(Bx)\) desplazado a la derecha por\(\dfrac{C}{B}\) y hacia arriba por\(D\).
6. Esboce las asíntotas verticales, que ocurren en\(x=\dfrac{C}{B}+\dfrac{\pi}{2| B |}k\), donde\(k\) es un entero impar.
7. Traza tres puntos de referencia cualquiera y dibuja la gráfica a través de estos puntos.

Ejemplo\(\PageIndex{2}\): Graphing One Period of a Shifted Tangent Function

Grafica un periodo de la función\(y=−2\tan(\pi x+\pi)−1\).

Solución

• Paso 1. La función ya está escrita en el formulario\(y=A\tan(Bx−C)+D\).
• Paso 2. \(A=−2\), así que el factor de estiramiento es\(|A|=2\).
• Paso 3. \(B=\ pi\), entonces el periodo es\(P=\dfrac{\pi}{| B |}=\dfrac{\pi}{pi}=1\).
• Paso 4. \(C=−\ pi\), así que el desplazamiento de fase es\(CB=\dfrac{−\pi}{\pi}=−1\).
• Paso 5-7. Las asíntotas están en\(x=−\dfrac{3}{2}\) y\(x=−\dfrac{1}{2}\) y los tres puntos de referencia recomendados son\((−1.25,1)\),\((−1,−1)\), y\((−0.75,−3)\). La gráfica se muestra en la Figura\(\PageIndex{5}\).

Figura\(\PageIndex{5}\)

Análisis

Tenga en cuenta que esta es una función decreciente porque\(A<0\).

Ejercicio\(\PageIndex{2}\)

¿Cómo se\(\PageIndex{2}\) vería diferente la gráfica en Ejemplo si hiciéramos\(A=2\) en lugar de hacerlo\(−2\)?

Contestar

Se reflejaría a través de la línea\(y=−1\), convirtiéndose en una función cada vez mayor.

Cómo: Dada la gráfica de una función tangente, identificar estiramientos horizontales y verticales.

1. Encuentra el periodo\(P\) a partir del espaciado entre asíntotas verticales sucesivas o intersecciones x.
2. Escribir\(f(x)=A\tan \left (\dfrac{\pi}{P}x \right )\).
3. Determine un punto conveniente\((x,f(x))\) en la gráfica dada y utilícelo para determinar\(A\).

Ejemplo\(\PageIndex{3}\): Identifying the Graph of a Stretched Tangent

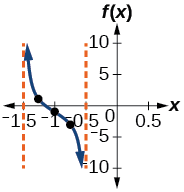
Encuentra una fórmula para la función graficada en la Figura\(\PageIndex{6}\).

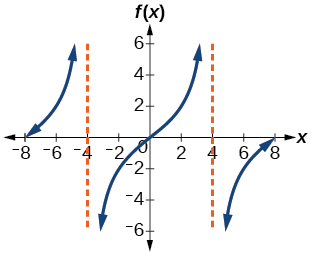
Figura\(\PageIndex{6}\): Una función tangente estirada

Solución

La gráfica tiene la forma de una función tangente.

• Paso 1. Un ciclo se extiende de\(–4\) a\(4\), entonces el periodo es\(P=8\). Ya que\(P=\dfrac{\pi}{| B |}\), tenemos\(B=\dfrac{π}{P}=\dfrac{\pi}{8}\).
• Paso 2. La ecuación debe tener la forma\(f(x)=A\tan \left (\dfrac{\pi}{8}x \right )\).
• Paso 3. Para encontrar el estiramiento vertical\(A\), podemos usar el punto\((2,2)\). \[\begin{align*} 2&=A\tan \left (\dfrac{\pi}{8}\cdot 2 \right )\\ &=A\tan \left (\dfrac{\pi}{4} \right ) \end{align*}\]

Porque\(\tan \left (\dfrac{\pi}{4} \right )=1\),\(A=2\).

Esta función tendría una fórmula\(f(x)=2\tan \left (\dfrac{\pi}{8}x \right )\).

Ejercicio\(\PageIndex{3}\)

Encuentra una fórmula para la función en la Figura\(\PageIndex{7}\).

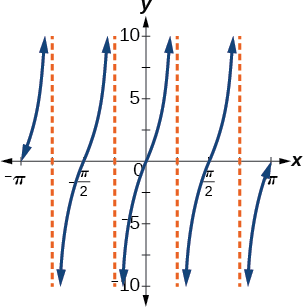
Figura\(\PageIndex{7}\)

Contestar

\(g(x)=4\tan(2x)\)

Analizando las Gráficas de\(y = \sec x\) y\(y = \csc x\)

La secante se definió por la identidad recíproca\(sec \, x=\dfrac{1}{\cos x}\). Observe que la función es indefinida cuando el coseno está\(0\), llevando a asíntotas verticales at\(\dfrac{\pi}{2}\),\(\dfrac{3\pi}{2}\) etc. Debido a que el coseno nunca está más que\(1\) en valor absoluto, la secante, siendo la recíproca, nunca será menor que\(1\) en valor absoluto.

Podemos graficar\(y=\sec x\) observando la gráfica de la función coseno porque estas dos funciones son recíprocas entre sí. Ver Figura\(\PageIndex{8}\). El gráfico del coseno se muestra como una onda naranja discontinua para que podamos ver la relación. Donde la gráfica de la función coseno disminuye, la gráfica de la función secante aumenta. Donde la gráfica de la función coseno aumenta, la gráfica de la función secante disminuye. Cuando la función coseno es cero, la secante no está definida.

La gráfica secante tiene asíntotas verticales en cada valor de\(x\) donde la gráfica coseno cruza el\(x\) eje -eje; las mostramos en la gráfica de abajo con líneas verticales discontinuas, pero no mostrará todas las asíntotas explícitamente en todas las gráficas posteriores que involucren a la secante y a la cosecante.

Tenga en cuenta que, debido a que el coseno es una función par, la secante también es una función par. Es decir,\(\sec(−x)=\sec x\).

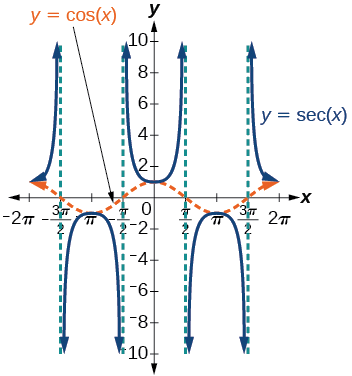
Figura\(\PageIndex{8}\): Gráfico de la función secante,\(f(x)=\sec x=\dfrac{1}{\cos x}\)

Como hicimos para la función tangente, volveremos a referirnos a la constante\(| A |\) como el factor de estiramiento, no la amplitud.

CARACTERÍSTICAS DEL GRAFO\(Y = A \sec(Bx)\)

• El factor de estiramiento es\(| A |\).
• El periodo es\(\dfrac{2\pi}{| B |}\).
• El dominio es\(x≠\dfrac{\pi}{2| B |}k\), donde\(k\) es un entero impar.
• El rango es\((−∞,−|A|]∪[|A|,∞)\).
• Las asíntotas verticales ocurren en\(x=\dfrac{\pi}{2| B |}k\), donde\(k\) es un entero impar.
• No hay amplitud.
• \(y=A\sec(Bx)\)es una función par porque el coseno es una función par.

Similar a la secante, la cosecante se define por la identidad recíproca\(\csc x=\dfrac{1}{\sin x}\). Observe que la función es indefinida cuando el seno está\(0\), conduciendo a una asíntota vertical en la gráfica at\(0\)\(\pi\),, etc. Dado que el seno nunca es más que\(1\) en valor absoluto, el cosecante, siendo el recíproco, nunca será menor que\(1\) en valor absoluto.

Podemos graficar\(y=\csc x\) observando la gráfica de la función sinusoidal porque estas dos funciones son recíprocas entre sí. Ver Figura\(\PageIndex{7}\). El gráfico de seno se muestra como una onda naranja discontinua para que podamos ver la relación. Donde la gráfica de la función sinusoidal disminuye, la gráfica de la función cosecante aumenta. Donde la gráfica de la función sinusoidal aumenta, la gráfica de la función cosecante disminuye.

La gráfica cosecante tiene asíntotas verticales en cada valor de\(x\) donde la gráfica sinusoidal cruza el\(x\) eje -eje; las mostramos en la gráfica de abajo con líneas verticales discontinuas.

Tenga en cuenta que, dado que seno es una función impar, la función cosecante también es una función impar. Es decir,\(\csc(−x)=−\csc x\).

La gráfica de cosecante, que se muestra en la Figura\(\PageIndex{9}\), es similar a la gráfica de secante.

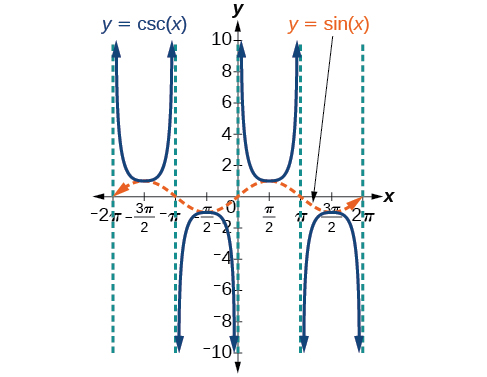
Figura\(\PageIndex{9}\): La gráfica de la función cosecante,\(f(x)=\csc x=\frac{1}{\sin x}\)

CARACTERÍSTICAS DEL GRAFO\(Y = A \csc(Bx)\)

• El factor de estiramiento es\(| A |\).
• El periodo es\(\dfrac{2\pi}{|B|}\).
• El dominio es\(x≠\dfrac{\pi}{|B|}k\), donde\(k\) es un entero.
• El rango es\((−∞,−|A|]∪[|A|,∞)\).
• Las asíntotas ocurren en\(x=\dfrac{\pi}{| B |}k\), donde\(k\) es un entero.
• \(y=A\csc(Bx)\)es una función impar porque seno es una función impar.

Graficando variaciones de\(y = \sec x\) y\(y= \csc x\)

Para versiones desplazadas, comprimidas y/o estiradas de las funciones secante y cosecante, podemos seguir métodos similares a los que usamos para tangente y cotangente. Es decir, ubicamos las asíntotas verticales y también evaluamos las funciones para algunos puntos (específicamente los extremos locales). Si queremos graficar solo un periodo, podemos elegir el intervalo para el periodo en más de una forma. El procedimiento para secante es muy similar, porque la identidad de cofunción significa que la gráfica secante es la misma que la gráfica cosecante desplazó medio periodo a la izquierda. Los desplazamientos verticales y de fase se pueden aplicar a la función cosecante de la misma manera que para la secante y otras funciones.Las ecuaciones se convierten en las siguientes.

\[y=A\sec(Bx−C)+D\]

\[y=A\csc(Bx−C)+D\]

Características de la gráfica de\(Y = A\sec(Bx−C)+D\)

• El factor de estiramiento es\(|A|\).
• El periodo es\(\dfrac{2\pi}{|B|}\).
• El dominio es\(x≠\dfrac{C}{B}+\dfrac{\pi}{2| B |}k\), donde\(k\) es un entero impar.
• El rango es\((−∞,−|A|]∪[|A|,∞)\).
• Las asíntotas verticales ocurren en\(x=\dfrac{C}{B}+\dfrac{π}{2| B |}k\), donde\(k\) es un entero impar.
• No hay amplitud.
• \(y=A\sec(Bx)\)es una función par porque el coseno es una función par.

Características de la gráfica de\(Y = A\csc(Bx−C)+D\)

1. El factor de estiramiento es\(|A|\).
2. El periodo es\(\dfrac{2\pi}{|B|}\).
3. El dominio es\(x≠\dfrac{C}{B}+\dfrac{\pi}{2| B |}k\), donde\(k\) es un entero.
4. El rango es\((−∞,−|A|]∪[|A|,∞)\).
5. Las asíntotas verticales ocurren en\(x=\dfrac{C}{B}+\dfrac{\pi}{|B|}k\), donde\(k\) es un entero.
6. No hay amplitud.
7. \(y=A\csc(Bx)\)es una función impar porque seno es una función impar.

COMO: Dada una función de la forma\(y=A\sec(Bx)\), graph one period

1. Expresar la función dada en el formulario\(y=A\sec(Bx)\).
2. Identificar el factor de estiramiento/compresión,\(|A|\).
3. Identificar\(B\) y determinar el periodo,\(P=\dfrac{2\pi}{| B |}\).
4. Esbozar la gráfica de\(y=A\cos(Bx)\).
5. Utilice la relación recíproca entre\(y=\cos \, x\) y\(y=\sec \, x\) para dibujar la gráfica de\(y=A\sec(Bx)\).
6. Dibuje las asíntotas.
7. Traza dos puntos de referencia cualesquiera y dibuja la gráfica a través de estos puntos.

Ejemplo\(\PageIndex{4}\): Graphing a Variation of the Secant Function

Gráfica un periodo de\(f(x)=2.5\sec(0.4x)\).

Solución

• Paso 1. La función dada ya está escrita en la forma general,\(y=A\sec(Bx)\).
• Paso 2. \(A=2.5\)por lo que el factor de estiramiento es\(2.5\).
• Paso 3. \(B=0.4\)así\(P=\dfrac{2\pi}{0.4}=5\pi\). El periodo es\(5\pi\) unidades.
• Paso 4. Dibuja la gráfica de la función\(g(x)=2.5\cos(0.4x)\).
• Paso 5. Utilizar la relación recíproca de las funciones coseno y secante para dibujar la función cosecante.
• Pasos 6—7. Esbozar dos asíntotas en\(x=1.25\pi\) y\(x=3.75\pi\). Podemos utilizar dos puntos de referencia, el mínimo local en\((0,2.5)\) y el máximo local en\((2.5\pi,−2.5)\). En la figura se\(\PageIndex{10}\) muestra la gráfica.

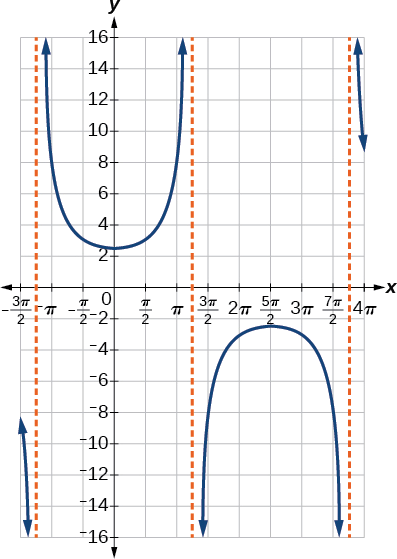
Figura\(\PageIndex{10}\)

Ejercicio\(\PageIndex{4}\)

Gráfica un periodo de\(f(x)=−2.5\sec(0.4x)\).

Contestar

Se trata de una reflexión vertical de la gráfica anterior porque\(A\) es negativa.

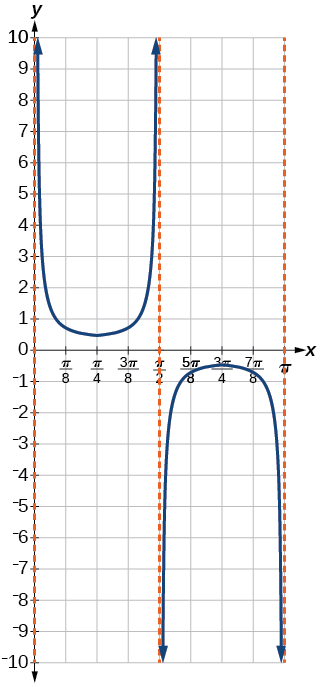
Figura\(\PageIndex{11}\)

Q&A: ¿El desplazamiento vertical y el estiramiento/compresión afectan el rango de la secante?

Sí. El rango de\(f(x)=A\sec(Bx−C)+D\) es\((−∞,−|A|+D]∪[|A|+D,∞)\).

Cómo: Dada una función de la forma\(f(x)=A\sec(Bx−C)+D\), graph one period.

1. Expresar la función dada en el formulario\(y=A \sec(Bx−C)+D\).
2. Identificar el factor de estiramiento/compresión,\(| A |\).
3. Identificar\(B\) y determinar el periodo,\(\dfrac{2\pi}{|B|}\).
4. Identificar\(C\) y determinar el desplazamiento de fase,\(\dfrac{C}{B}\).
5. Dibuja la gráfica de\(y=A \sec(Bx)\). pero muévala hacia la derecha por\(\dfrac{C}{B}\) y hacia arriba por\(D\).
6. Esboce las asíntotas verticales, que ocurren en\(x=\dfrac{C}{B}+\dfrac{\pi}{2| B |}k\), donde\(k\) es un entero impar.

Ejemplo\(\PageIndex{5}\): Graphing a Variation of the Secant Function

Gráfica un periodo de\(y=4\sec \left (\dfrac{\pi}{3x}−\dfrac{\pi}{2} \right )+1\).

Solución

• Paso 1. Expresar la función dada en el formulario\(y=4\sec \left (\dfrac{\pi}{3x}−\dfrac{\pi}{2} \right )+1\).
• Paso 2. El factor de estiramiento/compresión es\(| A |=4\).
• Paso 3. El periodo es

\[\begin{align*} \dfrac{2\pi}{|B|}&= \dfrac{2\pi}{\dfrac{\pi}{3}}\\ &= 2\pi \cdot \dfrac{3}{\pi}\\ &= 6 \end{align*}\]

• Paso 4. El desplazamiento de fase es

\[\begin{align*} \dfrac{C}{B}&= \dfrac{\dfrac{\pi}{2}}{\dfrac{\pi}{3}}\\ &= \dfrac{\pi}{2}\cdot \dfrac{3}{\pi}\\ &= 1.5 \end{align*}\]

• Paso 5. Dibuja la gráfica de\(y=A\sec(Bx)\), pero muévala hacia la derecha\(\dfrac{C}{B}=1.5\) y hacia arriba por\(D=6\).
• Paso 6. Dibuje las asíntotas verticales, que ocurren en\(x=0\),\(x=3\), y\(x=6\). Hay un mínimo local en\((1.5,5)\) y un máximo local en\((4.5,−3)\). En la figura se\(\PageIndex{12}\) muestra la gráfica.

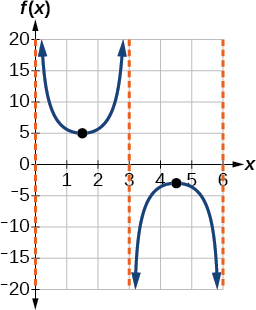
Figura\(\PageIndex{12}\)

Ejercicio\(\PageIndex{5}\)

Gráfica un periodo de\(f(x)=−6\sec(4x+2)−8\).

Contestar

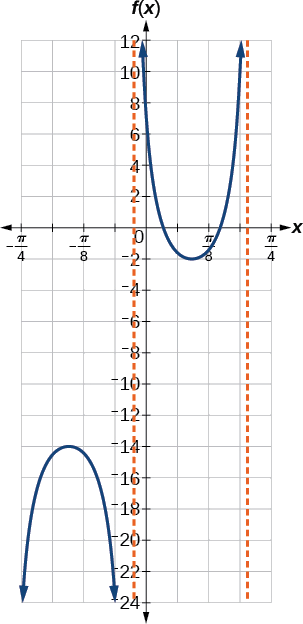
Figura\(\PageIndex{13}\)

Q&A: El dominio de\(\csc \, x\) was given to be all \(x\) such that \(x≠k\pi\) for any integer \(k\). Would the domain of \(y=A\csc(Bx−C)+D\) be \(x≠\dfrac{C+k\pi}{B}\)?

Sí. Los puntos excluidos del dominio siguen las asíntotas verticales. Sus ubicaciones muestran el desplazamiento horizontal y la compresión o expansión implícita por la transformación a la entrada de la función original.

Cómo: Dada una función de la forma\(y=A\csc(Bx)\), graph one period.

1. Expresar la función dada en el formulario\(y=A\csc(Bx)\).
2. \(|A|\).
3. Identificar\(B\) y determinar el periodo,\(P=\dfrac{2\pi}{| B |}\).
4. Dibuja la gráfica de\(y=A\sin(Bx)\).
5. Utilice la relación recíproca entre\(y=sin \, x\) y\(y=\csc \, x\) para dibujar la gráfica de\(y=A\csc(Bx)\).
6. Dibuje las asíntotas.
7. Traza dos puntos de referencia cualesquiera y dibuja la gráfica a través de estos puntos.

Ejemplo\(\PageIndex{6}\): Graphing a Variation of the Cosecant Function

Gráfica un periodo de\(f(x)=−3\csc(4x)\).

Solución

• Paso 1. La función dada ya está escrita en la forma general,\(y=A\csc(Bx)\).
• Paso 2. \(| A |=| −3 |=3\), por lo que el factor de estiramiento es\(3\).
• Paso 3. \(B=4\), entonces\(P=\dfrac{2\pi}{4}=\dfrac{\pi}{2}\). El periodo es\(\dfrac{\pi}{2}\) unidades.
• Paso 4. Dibuja la gráfica de la función\(g(x)=−3\sin(4x)\).
• Paso 5. Utilizar la relación recíproca de las funciones seno y cosecante para dibujar la función cosecante.
• Pasos 6—7. Dibuje tres asíntotas en\(x=0\),\(x=\dfrac{\pi}{4}\), y\(x=\dfrac{\pi}{2}\). Podemos utilizar dos puntos de referencia, el máximo local en\(\left (\dfrac{\pi}{8},−3 \right )\) y el mínimo local en\(\left (\dfrac{3\pi}{8},3 \right )\). En la figura se\(\PageIndex{14}\) muestra la gráfica.

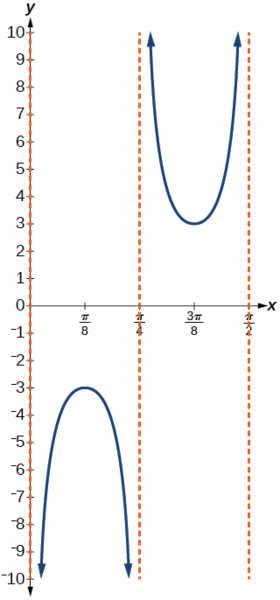
Figura\(\PageIndex{14}\)

Ejercicio\(\PageIndex{6}\)

Gráfica un periodo de\(f(x)=0.5\csc(2x)\).

Contestar

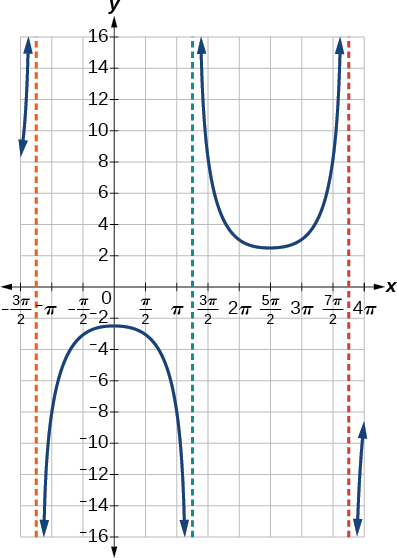
Figura\(\PageIndex{15}\)

Cómo: Dada una función de la forma\(f(x)=A \csc(Bx−C)+D\), graph one period

1. Expresar la función dada en el formulario\(y=A\csc(Bx−C)+D\).
2. Identificar el factor de estiramiento/compresión,\(|A|\).
3. Identificar\(B\) y determinar el periodo,\(\dfrac{2\pi}{| B |}\).
4. Identificar\(C\) y determinar el desplazamiento de fase,\(\dfrac{C}{B}\).
5. Dibuja la gráfica de\(y=A\csc(Bx)\) pero muévala hacia la derecha y hacia arriba por\(D\).
6. Esboce las asíntotas verticales, que ocurren en\(x=\dfrac{C}{B}+\dfrac{\pi}{| B |}k\), donde\(k\) es un entero.

Ejemplo\(\PageIndex{7}\): Graphing a Vertically Stretched, Horizontally Compressed, and Vertically Shifted Cosecant

Esbozar una gráfica de\(y=2\csc \left (\dfrac{\pi}{2}x \right )+1\). ¿Cuáles son el dominio y el rango de esta función?

Solución

• Paso 1. Expresar la función dada en el formulario\(y=2\csc \left (\dfrac{\pi}{2}x \right )+1\).
• Paso 2. Identificar el factor de estiramiento/compresión,\(| A |=2\).
• Paso 3. El periodo es\(\dfrac{2\pi}{| B |}=\dfrac{2\pi}{\dfrac{\pi}{2}}=2\pi⋅\dfrac{2}{\pi}=4\).
• Paso 4. El desplazamiento de fase es\(\dfrac{0}{\dfrac{\pi}{2}}=0\).
• Paso 5. Dibuja la gráfica de\(y=A\csc(Bx)\) pero muévala hacia arriba\(D=1\).
• Paso 6. Dibuje las asíntotas verticales, que ocurren en\(x=0\),\(x=2\),\(x=4\).

La gráfica para esta función se muestra en la Figura\(\PageIndex{16}\).

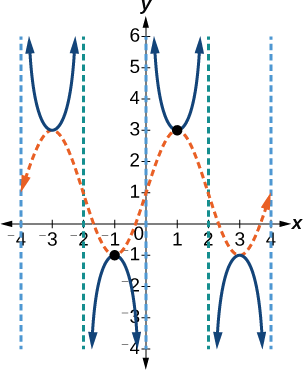
Figura\(\PageIndex{16}\): Una función cosecante transformada

Análisis

Las asíntotas verticales mostradas en la gráfica marcan un periodo de la función, y los extremos locales en este intervalo se muestran por puntos. Observe cómo la gráfica del cosecante transformado se relaciona con la gráfica de\(f(x)=2\sin \left (\frac{\pi}{2}x \right )+1\), mostrada como la onda discontinua naranja.

Ejercicio\(\PageIndex{7}\)

Dada la gráfica de que\(f(x)=2\cos \left (\frac{\pi}{2}x \right )+1\) se muestra en la Figura\(\PageIndex{17}\), bosquejar la gráfica de\(g(x)=2\sec \left (\dfrac{\pi}{2}x \right )+1\) en los mismos ejes.

Figura\(\PageIndex{17}\)

Contestar

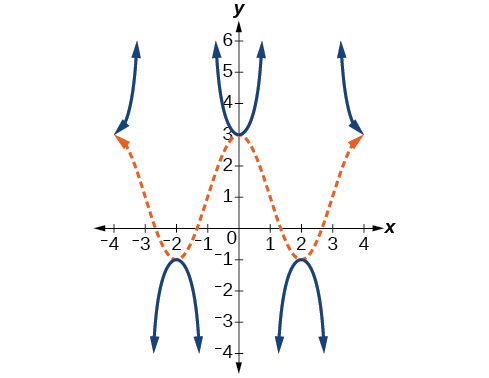
Figura\(\PageIndex{18}\)

Analizando la Gráfica de\(y = \cot x\)

La última función trigonométrica que necesitamos explorar es cotangente. La cotangente se define por la identidad recíproca\(cot \, x=\dfrac{1}{\tan x}\). Observe que la función no está definida cuando la función tangente es\(0\), lo que lleva a una asíntota vertical en la gráfica at\(0\)\(\pi\), etc. Dado que la salida de la función tangente es todos los números reales, la salida de la función cotangente también es todos los números reales.

Podemos graficar\(y=\cot x\) observando la gráfica de la función tangente porque estas dos funciones son recíprocas entre sí. Ver Figura\(\PageIndex{19}\). Donde la gráfica de la función tangente disminuye, la gráfica de la función cotangente aumenta. Donde la gráfica de la función tangente aumenta, la gráfica de la función cotangente disminuye.

La gráfica cotangente tiene asíntotas verticales en cada valor de\(x\) donde\(\tan x=0\); las mostramos en la gráfica de abajo con líneas discontinuas. Ya que la cotangente es el recíproco de la tangente,\(\cot x\) tiene asíntotas verticales en todos los valores de\(x\) dónde\(\tan x=0\), y\(\cot x=0\) en todos los valores de\(x\) dónde\(\tan x\) tiene sus asíntotas verticales.

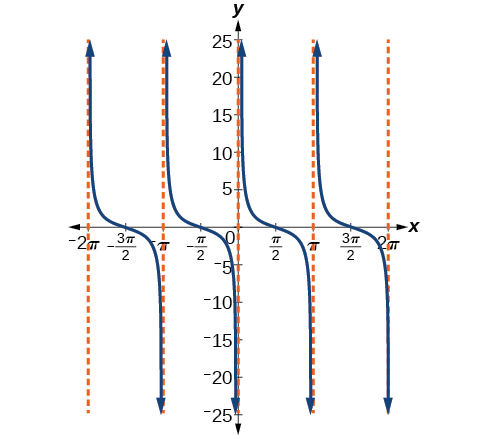
Figura\(\PageIndex{19}\): La función cotangente

Características de la gráfica de\(Y = A \cot(BX)\)

• El factor de estiramiento es\(|A|\).
• El periodo es\(P=\dfrac{\pi}{|B|}\).
• El dominio es\(x≠\dfrac{\pi}{|B|}k\), donde\(k\) es un entero.
• El rango es\((−∞,∞)\).
• Las asíntotas ocurren en\(x=\dfrac{\pi}{| B |}k\), donde\(k\) es un entero.
• \(y=A\cot(Bx)\)es una función impar.

Graficando variaciones de\(y =\cot x\)

Podemos transformar la gráfica de la cotangente de la misma manera que hicimos para la tangente. La ecuación se convierte en la siguiente.

\[y=A\cot(Bx−C)+D\]

PROPIEDADES DEL GRÁFICO DE\(Y = A \cot(Bx-c)+D\)

• El factor de estiramiento es\(| A |\).
• El periodo es\(\dfrac{\pi}{|B|}\)
• El dominio es\(x≠\dfrac{C}{B}+\dfrac{\pi}{| B |}k\), donde\(k\) es un entero.
• El rango es\((−∞,−|A|]∪[|A|,∞)\).
• Las asíntotas verticales ocurren en\(x=\dfrac{C}{B}+\dfrac{\pi}{| B |}k\), donde\(k\) es un entero.
• No hay amplitud.
• \(y=A\cot(Bx)\)es una función impar porque es el cociente de las funciones par e impar (coseno y seno, respectivamente)

Cómo: Dada una función cotangente modificada de la forma\(f(x)=A\cot(Bx)\),graph one period.

1. Exprese la función en el formulario\(f(x)=A\cot(Bx)\).
2. Identificar el factor de estiramiento,\(|A|\).
3. Identificar el periodo,\(P=\dfrac{\pi}{|B|}\).
4. Dibuja la gráfica de\(y=A\tan(Bx)\).
5. Trazar dos puntos de referencia cualesquiera.
6. Utilice la relación recíproca entre tangente y cotangente para dibujar la gráfica de\(y=Acot(Bx)\).
7. Dibuje las asíntotas.

Ejemplo\(\PageIndex{8}\): Graphing Variations of the Cotangent Function

Determine el factor de estiramiento, el período y el desplazamiento de fase de\(y=3\cot(4x)\), y luego dibuje una gráfica.

Solución

• Paso 1. Expresando la función en la forma\(f(x)=A\cot(Bx)\) da\(f(x)=3\cot(4x)\).
• Paso 2. El factor de estiramiento es\(|A|=3\).
• Paso 3. El periodo es\(P=\dfrac{\pi}{4}\).
• Paso 4. Esbozar la gráfica de\(y=3\tan(4x)\).
• Paso 5. Trazar dos puntos de referencia. Dos de esos puntos son\(\left (\dfrac{\pi}{16},3 \right )\) y\(\left (\dfrac{3\pi}{16},−3 \right )\).
• Paso 6. Utilizar la relación recíproca para dibujar\(y=3\cot(4x)\).
• Paso 7. Esbozar las asíntotas,\(x=0\),\(x=\dfrac{\pi}{4}\).

La gráfica naranja en la Figura\(\PageIndex{20}\) muestra\(y=3\tan(4x)\) y la gráfica azul muestra\(y=3\cot(4x)\).

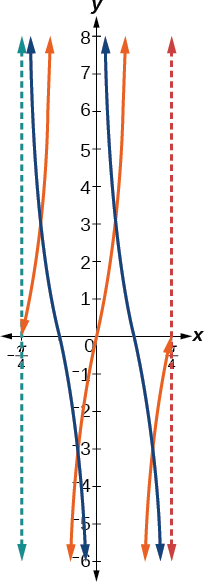
Figura\(\PageIndex{20}\)

Cómo: Dada una función cotangente modificada de la forma\(f(x)=A\cot(Bx−C)+D\), graph one period.

1. Exprese la función en el formulario\(f(x)=A\cot(Bx−C)+D\).
2. Identificar el factor de estiramiento,\(| A |\).
3. Identificar el periodo,\(P=\dfrac{\pi}{|B|}\).
4. Identificar el desplazamiento de fase,\(\dfrac{C}{B}\).
5. Dibuja la gráfica de\(y=A\tan(Bx)\) desplazado a la derecha por\(\dfrac{C}{B}\) y hacia arriba por\(D\).
6. Dibuje las asíntotas\(x=\dfrac{C}{B}+\dfrac{\pi}{| B |}k\), donde\(k\) es un entero.
7. Traza tres puntos de referencia cualquiera y dibuja la gráfica a través de estos puntos.

Ejemplo\(\PageIndex{9}\): Graphing a Modified Cotangent

Esbozar una gráfica de un periodo de la función\(f(x)=4\cot \left (\dfrac{\pi}{8}x−\dfrac{\pi}{2} \right )−2\).

Solución

• Paso 1. La función ya está escrita en la forma general\(f(x)=A\cot(Bx−C)+D\).
• Paso 2. \(A=4\), por lo que el factor de estiramiento es\(4\).
• Paso 3. \(B=\dfrac{\pi}{8}\), así es el periodo\(P=\dfrac{\pi}{| B |}=\dfrac{\pi}{\dfrac{\pi}{8}}=8\).
• Paso 4. \(C=\dfrac{\pi}{2}\), por lo que el desplazamiento de fase es\(CB=\dfrac{\dfrac{\pi}{2}}{\dfrac{\pi}{8}}=4\).
• Paso 5. Dibujamos\(f(x)=4\tan \left (\dfrac{\pi}{8}x−\dfrac{\pi}{2} \right )−2\).
• Paso 6-7. Tres puntos que podemos utilizar para guiar la gráfica son\((6,2)\),\((8,−2)\), y\((10,−6)\). Utilizamos la relación recíproca de tangente y cotangente para dibujar\(f(x)=4\cot \left (\dfrac{\pi}{8}x−\dfrac{\pi}{2} \right )−2\).
• Paso 8. Las asíntotas verticales son\(x=4\) y\(x=12\).

La gráfica se muestra en la Figura\(\PageIndex{21}\).

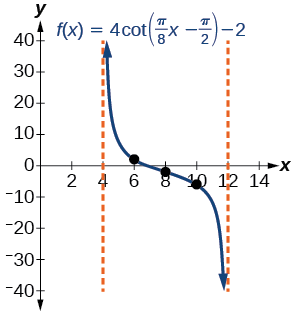
Figura\(\PageIndex{21}\): Un periodo de una función cotangente modificada

Uso de las Gráficas de Funciones Trigonométricas para Resolver Problemas del Mundo Real

Muchos escenarios del mundo real representan funciones periódicas y pueden ser modelados por funciones trigonométricas. Como ejemplo, volvamos al escenario desde el abridor de sección. ¿Alguna vez has observado el haz formado por la luz giratoria en un carro de policía y te has preguntado sobre el movimiento del haz de luz en sí a través de la pared? El comportamiento periódico de la distancia que la luz brilla en función del tiempo es obvio, pero ¿cómo determinamos la distancia? Podemos usar la función tangente.

Ejemplo\(\PageIndex{10}\): Using Trigonometric Functions to Solve Real-World Scenarios

Supongamos que la función\(y=5\tan(\dfrac{\pi}{4}t)\) marca la distancia en el movimiento de un haz de luz desde la parte superior de un carro de policía a través de una pared donde\(t\)\(y\) está el tiempo en segundos y es la distancia en pies desde un punto en la pared directamente enfrente del auto policial.

1. Encontrar e interpretar el factor de estiramiento y período.
2. Gráfica sobre el intervalo\([0,5]\).
3. Evaluar\(f(1)\) y discutir el valor de la función en esa entrada.

Solución

1. Sabemos por la forma general de\(y=A\tan(Bt)\) que\(| A |\) es el factor de estiramiento y\(\dfrac{\pi}{B}\) es el periodo.

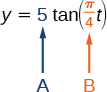
Figura\(\PageIndex{22}\)

Vemos que el factor de estiramiento es\(5\). Esto significa que el haz de luz se habrá movido\(5\) pies después de la mitad del período.

El periodo es\(\dfrac{\pi}{\tfrac{\pi}{4}}=\dfrac{\pi}{1}⋅\dfrac{4}{\pi}=4\). Esto significa que cada\(4\) segundo, el haz de luz barre la pared. La distancia desde el lugar frente al carro de la policía se hace más grande a medida que se acerca el auto de policía.

2. Para graficar la función, dibujamos una asíntota en\(t=2\) y usamos el factor de estiramiento y el período. Ver Figura\(\PageIndex{23}\)

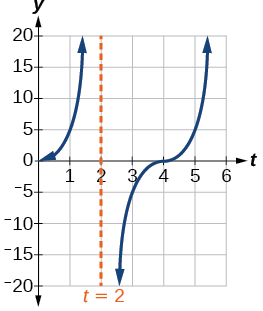
Figura\(\PageIndex{23}\)

3. periodo:\(f(1)=5\tan(\frac{\pi}{4}(1))=5(1)=5\); después del\(1\) segundo, la viga de se ha movido\(5\) pies desde el lugar frente al auto de policía.

Medios

Acceda a estos recursos en línea para obtener instrucción adicional y práctica con gráficas de otras funciones trigonométricas.

• Graficando la Tangente
• Graficando Cosecante y Secante
• Graficando la cotangente

Ecuaciones Clave

Función tangente desplazada, comprimida y/o estirada	\(y=A \tan(Bx−C)+D\)
Función secante desplazada, comprimida y/o estirada	\(y=A \sec(Bx−C)+D\)
Función cosecante desplazada, comprimida y/o estirada	\(y=A \csc(Bx−C)+D\)
Función cotangente desplazada, comprimida y/o estirada	\(y=A \cot(Bx−C)+D\)

Conceptos clave

• La función tangente tiene punto\(π\).
• \(f( x )=A\tan( Bx−C )+D\)es una tangente con estiramiento/compresión vertical y/u horizontal y desplazamiento. Ver Ejemplo\(\PageIndex{1}\)\(\PageIndex{2}\), Ejemplo y Ejemplo\(\PageIndex{3}\).
• La secante y la cosecante son ambas funciones periódicas con un periodo de\(2\pi\). \(f( x )=A\sec( Bx−C )+D\)da una gráfica de función secante desplazada, comprimida y/o estirada. Ver Ejemplo\(\PageIndex{4}\) y Ejemplo\(\PageIndex{5}\).
• \(f( x )=A\csc( Bx−C )+D\)da una gráfica de función cosecante desplazada, comprimida y/o estirada. Ver Ejemplo\(\PageIndex{6}\) y Ejemplo\(\PageIndex{7}\).
• La función cotangente tiene período\(\pi\) y asíntotas verticales a\(0,±\pi,±2\pi\),...
• El rango de cotangente es\(( −∞,∞ )\), y la función está disminuyendo en cada punto de su rango.
• La cotangente es cero en\(±\dfrac{\pi}{2},±\dfrac{3\pi}{2}\),...
• \(f(x)=A\cot(Bx−C)+D\)es una cotangente con estiramiento/compresión vertical y/u horizontal y desplazamiento. Ver Ejemplo\(\PageIndex{8}\) y Ejemplo\(\PageIndex{9}\).
• Los escenarios del mundo real se pueden resolver usando gráficos de funciones trigonométricas. Ver Ejemplo\(\PageIndex{10}\).