12.R: Introducción al Cálculo (Revisión)
- Page ID
- 121497
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)12.1: Encontrar límites - Enfoques numéricos y gráficos
Para los ejercicios 1-6, usa la Figura a continuación.
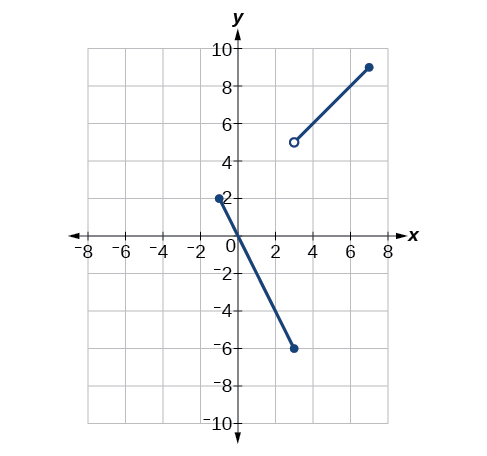
1)\(\lim \limits_{x \to -1^+}f(x)\)
- Contestar
-
\(2\)
2)\(\lim \limits_{x \to -1^-}f(x)\)
3)\(\lim \limits_{x \to -1}f(x)\)
- Contestar
-
no existe
4)\(\lim \limits_{x \to 3}f(x)\)
5) ¿A qué valores de la función\(x\) es discontinua? ¿Qué condición de continuidad se viola?
- Contestar
-
Discontinuo en\(x=-1\left (\lim \limits_{x \to a}f(x) \text{ does not exist} \right )\),\(x=3\left (\text{ jump discontinuity} \right )\), y\(x=7\left (\lim \limits_{x \to a}f(x) \text{ does not exist} \right )\).
6) Utilizando la Tabla a continuación, estimar\(\lim \limits_{x \to 0}f(x)\).
| \(x\) | \(F(x)\) |
|---|---|
| \ (x\) ">−0.1 | \ (F (x)\) ">2.875 |
| \ (x\) ">−0.01 | \ (F (x)\) ">2.92 |
| \ (x\) ">−0.001 | \ (F (x)\) ">2.998 |
| \ (x\) ">0 | \ (F (x)\) ">Sin definir |
| \ (x\) ">0.001 | \ (F (x)\) ">2.9987 |
| \ (x\) ">0.01 | \ (F (x)\) ">2.865 |
| \ (x\) ">0.1 | \ (F (x)\) ">2.78145 |
| \ (x\) ">0.15 | \ (F (x)\) ">2.678 |
- Contestar
-
\(3\)
Para los ejercicios 7-9, con el uso de una utilidad gráfica, utilizar evidencia numérica o gráfica para determinar los límites izquierdo y derecho de la función dada como\(x\) enfoques\(a\). Si la función tiene límite como\(x\) aproximaciones\(a\), indicarlo. Si no, discuta por qué no hay límite.
7)\(f(x)=\begin{cases} \left | x \right |-1 & \text{ if } x\neq 1 \\ x^3 & \text{ if } x= 1 \end{cases} a=1\)
8)\(f(x)=\begin{cases} \dfrac{1}{x+1} & \text{ if } x= -2 \\ (x+1)^2 & \text{ if } x\neq -2 \end{cases} a=-2\)
- Contestar
-
\(\lim \limits_{x \to -2}f(x)=1\)
9)\(f(x)=\begin{cases} \sqrt{x+3} & \text{ if } x<1 \\ -\sqrt[3]{x} & \text{ if } x>1 \end{cases} a=1\)
12.2: Encontrar límites - Propiedades de límites
Para los ejercicios 1-6, encuentra los límites si\(\lim \limits_{x \to c} f(x)=-3\) y\(\lim \limits_{x \to c} g(x)=5\).
1)\(\lim \limits_{x \to c} (f(x)+g(x))\)
- Contestar
-
\(2\)
2)\(\lim \limits_{x \to c} \dfrac{f(x)}{g(x)}\)
3)\(\underset{x \to c}{\lim } (f(x)\cdot g(x))\)
- Contestar
-
\(-15\)
4)\(\lim \limits_{x \to 0^+} f(x), f(x)=\begin{cases} 3x^2+2x+1 & x>0 \\ 5x+3 & x<0 \end{cases}\)
5)\(\lim \limits_{x \to 0^-} f(x), f(x)=\begin{cases} 3x^2+2x+1 & x>0 \\ 5x+3 & x<0 \end{cases}\)
- Contestar
-
\(3\)
6)\(\lim \limits_{x \to 3^+} (3x-〚x〛)\)
Para los ejercicios 7-11, evaluar los límites utilizando técnicas algebraicas.
7)\(\lim \limits_{h \to 0} \left ( \dfrac{(h+6)^2-36}{h} \right )\)
- Contestar
-
\(12\)
8)\(\lim \limits_{x \to 25} \left ( \dfrac{x^2-625}{\sqrt{x}-5} \right )\)
9)\(\lim \limits_{x \to 1} \left ( \dfrac{-x^2-9x}{x} \right )\)
- Contestar
-
\(-10\)
10)\(\lim \limits_{x \to 4} \left ( \dfrac{7-\sqrt{12x+1}}{x-4} \right )\)
11)\(\lim \limits_{x \to 3} \left ( \dfrac{\frac{1}{3}+\frac{1}{x}}{3+x} \right )\)
- Contestar
-
\(-\dfrac{1}{9}\)
12.3: Continuidad
Para los ejercicios 1-5, use evidencia numérica para determinar si el límite existe en\(x=a\). Si no, describa el comportamiento de la gráfica de la función en\(x=a\).
1)\(f(x)=\dfrac{-2}{x-4};\; a=4\)
2)\(f(x)=\dfrac{-2}{(x-4)^2};\; a=4\)
- Contestar
-
At\(x=4\), la función tiene una asíntota vertical.
3)\(f(x)=\dfrac{-x}{x^2-x-6};\; a=3\)
4)\(f(x)=\dfrac{6x^2+23x+20}{4x^2-25};\; a=-\dfrac{5}{2}\)
- Contestar
-
discontinuidad removible en\(a=-\dfrac{5}{2}\)
5)\(f(x)=\dfrac{\sqrt{x}-3}{9-x};\; a=9\)
Para los ejercicios 6-12, determinar dónde\(f(x)\) es continua la función dada. Donde no sea continuo, indique qué condiciones fallan, y clasifique las discontinuidades.
6)\(f(x)=x^2-2x-15\)
- Contestar
-
continuo en\((-\infty, \infty)\)
7)\(f(x)=\dfrac{x^2-2x-15}{x-5}\)
8)\(f(x)=\dfrac{x^2-2x}{x^2-4x+4}\)
- Contestar
-
discontinuidad removible en\(x=2\). \(f(2)\)no está definido, pero existen límites.
9)\(f(x)=\dfrac{x^3-125}{2x^2-12x+10}\)
10)\(f(x)=\dfrac{x^2-\frac{1}{x}}{2-x}\)
- Contestar
-
discontinuidad en\(x=0\) y\(x=2\). Ambos\(f(0)\) y no\(f(2)\) están definidos.
11)\(f(x)=\dfrac{x+2}{x^2-3x-10}\)
12)\(f(x)=\dfrac{x+2}{x^3+8}\)
- Contestar
-
discontinuidad removible en\(x=-2\). \(f(-2)\)no está definido.
12.4: Derivados
Para los ejercicios 1-5, encuentra la tasa promedio de cambio\(f(x)=\dfrac{f(x+h)-f(x)}{h}\).
1)\(f(x)=3x+2\)
2)\(f(x)=5\)
- Contestar
-
\(0\)
3)\(f(x)=\dfrac{1}{x+1}\)
4)\(f(x)=\ln (x)\)
- Contestar
-
\(f(x)=\dfrac{\ln (x+h)-\ln (x)}{h}\)
5)\(f(x)=e^{2x}\)
Para los ejercicios 6-7, encuentra la derivada de la función.
6)\(f(x)=4x-6\)
- Contestar
-
\(4\)
7)\(f(x)=5x^2-3x\)
8) Encuentra la ecuación de la línea tangente a la gráfica de\(f(x)\) al\(x\) valor indicado. \[f(x)=-x^3+4x;\; x=2 \nonumber \]
- Contestar
-
\(y=-8x+16\)
9) Para el siguiente ejercicio, con la ayuda de una utilidad gráfica, explicar por qué la función no es diferenciable en todas partes en su dominio. Especificar los puntos donde la función no es diferenciable. \[f(x)=\dfrac{x}{\left | x \right |} \nonumber \]
10) Dado que el volumen de un cono circular derecho es\(V=\dfrac{1}{3}\pi r^2h\) y que un cono dado tiene una altura fija de\(9\) cm y longitud de radio variable, encuentre la tasa instantánea de cambio de volumen con respecto a la longitud del radio cuando el radio sea\(2\) cm. Dar una respuesta exacta en términos de\(π\).
- Contestar
-
\(12\pi \)
Prueba de práctica
Para los ejercicios 1-6, utilice la gráfica de\(f\) la Figura a continuación.
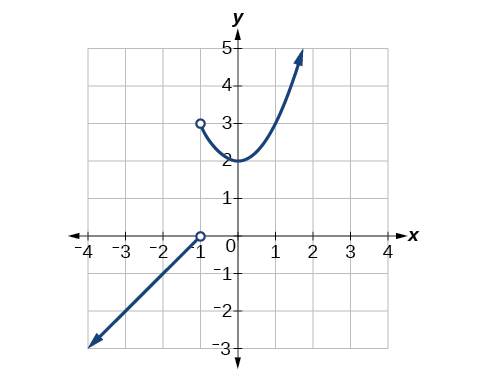
1)\(f(1)\)
- Contestar
-
\(3\)
2)\(\lim \limits_{x \to -1^+} f(x)\)
3)\(\lim \limits_{x \to -1^-} f(x)\)
- Contestar
-
\(0\)
4)\(\lim \limits_{x \to -1} f(x)\)
5)\(\lim \limits_{x \to -2} f(x)\)
- Contestar
-
\(-1\)
6) ¿A qué valores de\(x\) es\(f\) discontinuo? ¿Qué propiedad de continuidad se viola?
7)\(f(x)=\begin{cases} \dfrac{1}{3}-3 & \text{ if } x\leq 2 \\ x^3+1 & \text{ if } x>2 \end{cases} a=2\)
- Contestar
-
\(\lim \limits_{x \to 2^-} f(x)=-\dfrac{5}{2}a\)y\(\lim \limits_{x \to 2^+} f(x)=9\)
8)\(f(x)=\begin{cases} x^3+1 & \text{ if } x<1 \\ 3x^2-1 & \text{ if } x=1\; a=1 \\ -\sqrt{x+3}+4 & \text{ if } x>1 \end{cases}\)
Para los ejercicios 9-11, evaluar cada límite utilizando técnicas algebraicas.
9)\(\lim \limits_{x \to -5} \left ( \dfrac{\frac{1}{5}+\frac{1}{x}}{10+2x} \right )\)
- Contestar
-
\(-\dfrac{1}{50}\)
10)\(\lim \limits_{h \to 0} \left ( \dfrac{\sqrt{h^2+25}-5}{h^2} \right )\)
11)\(\lim \limits_{h \to 0} \left ( \dfrac{1}{h}-\dfrac{1}{h^2+h} \right )\)
- Contestar
-
\(1\)
Para los ejercicios 12-13, determinar si la función dada\(f\) es continua o no. Si es continuo, muestra por qué. Si no es continuo, indique qué condiciones fallan.
12)\(f(x)=\sqrt{x^2-4}\)
13)\(f(x)=\dfrac{x^3-4x^2-9x+36}{x^3-3x^2+2x-6}\)
- Contestar
-
discontinuidad removible en\(x=3\)
Para los ejercicios 14-16, utilice la definición de una derivada para encontrar la derivada de la función dada en\(x=a\).
14)\(f(x)=\dfrac{3}{5+2x}\)
15)\(f(x)=\dfrac{3}{\sqrt{x}}\)
- Contestar
-
\(f'(x)=-\dfrac{3}{2a^{\frac{3}{2}}}\)
16)\(f(x)=2x^2+9x\)
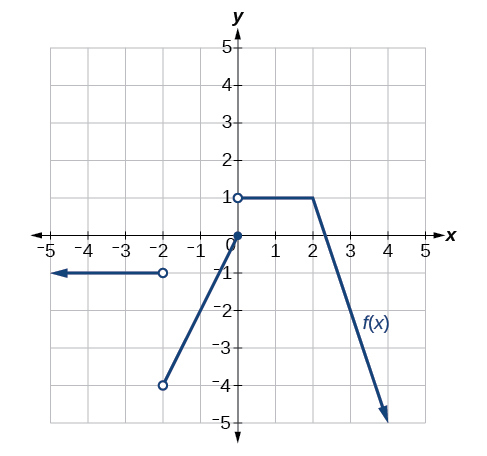
17) Para la gráfica de la siguiente Figura, determinar dónde la función es continua/discontinua y diferenciable/no diferenciable.
- Contestar
-
discontinuo en\(-2,0\), no diferenciable en\(-2,0, 2\).
Para los ejercicios 18-19, con la ayuda de una utilidad gráfica, explicar por qué la función no es diferenciable en todas partes en su dominio. Especificar los puntos donde la función no es diferenciable.
18)\(f(x)=\left | x-2 \right | - \left | x+2 \right |\)
19)\(f(x)=\dfrac{2}{1+e^{\frac{2}{x}}}\)
- Contestar
-
no diferenciable en\(x=0\) (sin límite)
Para los ejercicios 20-24, explicar la notación en palabras cuando la altura de un proyectil en pies,\(s\), es una función del tiempo\(t\) en segundos después del lanzamiento y viene dada por la función\(s(t)\).
20)\(s(0)\)
21)\(s(2)\)
- Contestar
-
la altura del proyectil en\(t=2\) segundos
22)\(s'(2)\)
23)\(\dfrac{s(2)-s(1)}{2-1}\)
- Contestar
-
la velocidad promedio de\(t=1\) a\(t=2\)
24)\(s(t)=0\)
Para los ejercicios 25-28, utilizar la tecnología para evaluar el límite.
25)\(\lim \limits_{x \to 0}\dfrac{\sin (x)}{3x}\)
- Contestar
-
\(\dfrac{1}{3}\)
26)\(\lim \limits_{x \to 0}\dfrac{\tan ^2(x)}{2x}\)
27)\(\lim \limits_{x \to 0}\dfrac{\sin (x)(1-\cos (x))}{2x^2}\)
- Contestar
-
\(0\)
28) Evaluar el límite a mano.
\[\lim \limits_{x \to 1}f(x), \text{ where } f(x)=\begin{cases} 4x-7 & x\neq 1 \\ x^2-4 & x= 1 \end{cases} \nonumber \]
¿A qué valor (s) de\(x\) es discontinua la función por debajo?
\[f(x)=\begin{cases} 4x-7 & x\neq 1 \\ x^2-4 & x= 1 \end{cases} \nonumber \]
Para los ejercicios 29-32, considere la función cuya gráfica aparece en la Figura.
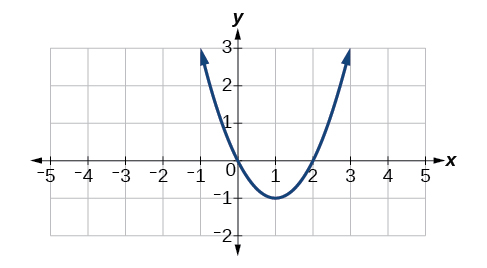
29) Encuentra la tasa promedio de cambio de la función de\(x=1\) a\(x=3\).
- Contestar
-
\(2\)
30) Encuentra todos los valores de\(x\) a los cuales\(f'(x)=0\).
- Contestar
-
\(x=1\)
31) Encontrar todos los valores de\(x\) a los que\(f'(x)\) no existe.
32) Encuentra una ecuación de la línea tangente a la gráfica\(f\) del punto indicado:\(f(x)=3x^2-2x-6,\; x=-2\)
- Contestar
-
\(y=-14x-18\)
Para los ejercicios 33-34, usa la función\(f(x)=x(1-x)^{\frac{2}{5}}\)
33) Grafica la función\(f(x)=x(1-x)^{\tfrac{2}{5}}\) ingresando\(f(x)=x\left ((1-x)^2 \right )^{\tfrac{1}{5}}\) y luego ingresando\(f(x)=x\left ((1-x)^{\tfrac{1}{5}} \right )^2\).
34) Explorar el comportamiento de la gráfica de\(f(x)\) alrededor\(x=1\) graficando la función en los siguientes dominios,\([0.9, 1.1], [0.99, 1.01], [0.999, 1.001]\), y\([0.9999, 1.0001]\). Utilice esta información para determinar si la función parece ser diferenciable en\(x=1\).
- Contestar
-
La gráfica no es diferenciable en\(x=1\) (cúspide).
Para los ejercicios 35-42, encuentra la derivada de cada una de las funciones usando la definición: \(\lim \limits_{h \to 0} \dfrac{f(x+h)-f(x)}{h}\)
35)\(f(x)=2x-8\)
36)\(f(x)=4x^2-7\)
- Contestar
-
\(f'(x)=8x\)
37)\(f(x)=x-\dfrac{1}{2}x^2\)
38)\(f(x)=\dfrac{1}{x+2}\)
- Contestar
-
\(f'(x)=-\dfrac{1}{(2+x)^2}\)
39)\(f(x)=\dfrac{3}{x-1}\)
40)\(f(x)=-x^3+1\)
- Contestar
-
\(f'(x)=-3x^2\)
41)\(f(x)=x^2+x^3\)
42)\(f(x)=\sqrt{x-1}\)
- Contestar
-
\(f'(x)=-\dfrac{1}{2\sqrt{x-1}}\)


