12.E: Introducción al Cálculo (Ejercicios)

Última actualización
Guardar como PDF

Page ID: 121507

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

12.1: Encontrar límites - Enfoques numéricos y gráficos

En esta sección, examinaremos enfoques numéricos y gráficos para identificar límites.

Verbal

1) Explicar la diferencia entre un valor at$x=a$ y el límite a medida que se$x$ aproxima$a$.

Contestar: El valor de la función, la salida, at$x=a$ es$f(a)$. Cuando$\lim \limits_{x \to a}f(x)$ se toma el, los valores de$x$ se acercan infinitamente$a$ pero nunca iguales$a$. Como los valores de$x$ aproximación$a$ desde la izquierda y la derecha, el límite es el valor al que se acerca la función.

2) Explicar por qué decimos que una función no tiene un límite como$x$ enfoques$a$ si, como$x$ enfoques$a$, el límite de la izquierda no es igual al límite de la derecha.

Gráfica

Para los ejercicios 3-14, estime los valores funcionales y los límites a partir de la gráfica de la función$f$ proporcionada en la Figura siguiente.

3)$\lim \limits_{x \to −2^−} f(x)$

Contestar: $-4$

4)$\lim \limits_{x \to −2^+ }f(x)$

5)$\lim \limits_{x \to −2 f(x)}$

Contestar: $-4$

6)$f(−2)$

7)$\lim \limits_{x \to −1^− f(x)}$

Contestar: $2$

8)$\lim \limits_{x \to 1^+} f(x)$

9)$\lim \limits_{x \to 1} f(x)$

Contestar: no existe

10)$f(1)$

11)$\lim \limits_{x \to 4^−} f(x)$

Contestar: $4$

12)$\lim \limits_{x \to 4^+} f(x)$

13)$\lim \limits_{x \to 4} f(x)$

Contestar: no existe

14)$f(4)$

Para los ejercicios 15-21, dibujar la gráfica de una función a partir de los valores funcionales y límites proporcionados.

15)$\lim \limits_{x \to 0^−} f(x)=2, \lim \limits_{x \to 0^+} f(x)=–3, \lim \limits_{x \to 2} f(x)=2, f(0)=4, f(2)=–1, f(–3) \text{ does not exist.}$

Contestar: Las respuestas variarán.

16)$\lim \limits_{x \to 2^−} f(x)=0,\lim \limits_{x \to 2^+} =–2,\lim \limits_{x \to 0} f(x)=3, f(2)=5, f(0)$

Contestar: Las respuestas variarán.

17)$\lim \limits_{ x \to 2^−} f(x)=2, \lim \limits_{ x \to 2^+} f(x)=−3, \lim \limits_{x \to 0} f(x)=5, f(0)=1, f(1)=0$

Contestar: Las respuestas variarán.

18)$\lim \limits_{x \to 3^−} f(x)=0, \lim \limits_{x \to 3^+} f(x)=5, \lim \limits_{x \to 5} f(x)=0, f(5)=4, f(3) \text{ does not exist.}$

Contestar: Las respuestas variarán.

19)$ \lim \limits_{ x \to 4} f(x)=6, \lim \limits_{ x \to 6^+} f(x)=−1, \lim \limits_{ x \to 0} f(x)=5, f(4)=6, f(2)=6$

Contestar: Las respuestas variarán.

20)$ \lim \limits_{ x \to −3} f(x)=2, \lim \limits_{ x \to 1^+} f(x)=−2, \lim \limits_{ x \to 3} f(x)=–4, f(–3)=0, f(0)=0$

Contestar: Las respuestas variarán.

21)$ \lim \limits_{ x \to π} f(x)=π^2, \lim \limits_{ x \to –π} f(x)=\dfrac{π}{2}, \lim \limits_{ x \to 1^-} f(x)=0, f(π)=\sqrt{2}, f(0) \text{ does not exist}.$

Contestar: Las respuestas variarán.

Para los ejercicios 22-26, utilice una calculadora gráfica para determinar el límite a los$5$ decimales a medida que se$x$ aproxima$0$.

22)$f(x)=(1+x)^{\frac{1}{x}}$

23)$g(x)=(1+x)^{\frac{2}{x}}$

Contestar: $7.38906$

24)$h(x)=(1+x)^{\frac{3}{x}}$

25)$i(x)=(1+x)^{\frac{4}{x}}$

Contestar: $54.59815$

26)$j(x)=(1+x)^{\frac{5}{x}}$

27) Con base en el patrón que observaste en los ejercicios anteriores, haz una conjetura en cuanto al límite de$f(x)=(1+x)^{\frac{6}{x}}, g(x)=(1+x)^{\frac{7}{x}},$ y$h(x)=(1+x)^{\frac{n}{x}}.$

Contestar: $e^6≈403.428794,e^7≈1096.633158, e^n$

Para los ejercicios 28-29, utilice una utilidad gráfica para encontrar evidencia gráfica para determinar los límites de la mano izquierda y derecha de la función dada como$x$ enfoques$a$. Si la función tiene un límite a medida que se$x$ aproxima$a$, indíquelo. Si no, discuta por qué no hay límite.

28)$(x)= \begin{cases} |x|−1, && \text{if }x≠1 \\ x^3, && \text{if }x=1 \end{cases} a=1 $

29)$(x)= \begin{cases} \frac{1}{x+1}, && \text{if } x=−2 \\ (x+1)^2, && \text{if } x≠−2 \end{cases} a=−2 $

Contestar: $\lim \limits_{x \to −2} f(x)=1$

Numérico

Para los ejercicios 30-38, utilizar evidencia numérica para determinar si el límite existe en$x=a$. En caso contrario, describa el comportamiento de la gráfica de la función near$x=a$. Redondear las respuestas a dos decimales.

30)$f(x)=\dfrac{x^2−4x}{16−x^2};a=4$

31)$f(x)=\dfrac{x^2−x−6}{x^2−9};a=3$

Contestar: $\lim \limits_{x \to 3} \left (\dfrac{x^2−x−6}{x^2−9} \right )=\dfrac{5}{6}≈0.83$

32)$f(x)=\dfrac{x^2−6x−7}{x^2– 7x};a=7$

33)$f(x)=\dfrac{x^2–1}{x^2–3x+2};a=1$

Contestar: $\lim \limits_{x \to 1} \left (\dfrac{x^2−1}{x^2−3x+2} \right )=−2.00$

34)$f(x)=\dfrac{1−x^2}{x^2−3x+2};a=1$

35)$f(x)=\dfrac{10−10x^2}{x^2−3x+2};a=1$

Contestar: $\lim \limits_{x \to 1} \left (\dfrac{10−10x^2}{x^2−3x+2} \right )=20.00$

36)$f(x)=\dfrac{x}{6x^2−5x−6};a=\dfrac{3}{2}$

37)$f(x)=\dfrac{x}{4x^2+4x+1};a=−\dfrac{1}{2}$

Contestar: $\lim \limits_{x \to \frac{−1}{2}} \left (\dfrac{x}{4x^2+4x+1} \right )$no existe. Los valores de función disminuyen sin límite a medida que$x$ se$-0.5$ aproxima desde la izquierda o la derecha

38)$f(x)=\frac{2}{x−4}; a=4$

Para los ejercicios 39-41, utilice una calculadora para estimar el límite preparando una tabla de valores. Si no hay límite, describa el comportamiento de la función a medida que$x$ se acerca al valor dado.

39)$\lim \limits_{x \to 0} \dfrac{7 \tan x}{3x}$

Contestar

$\lim \limits_{x \to 0} \dfrac{7 \tan x}{3x}=\dfrac{7}{3}$

$CNX_Precalc_Figure_12_01_202.jpg$

40)$\lim \limits_{x \to 4} \dfrac{x^2}{x−4}$

Contestar: $CNX_Precalc_Figure_12_01_203.jpg$

41)$\lim \limits_{x \to 0}\dfrac{2 \sin x}{4 \tan x}$

Contestar

$\lim \limits_{x \to 0} \dfrac{2 \sin x}{4 \tan x}=\dfrac{1}{2}$

$CNX_Precalc_Figure_12_01_204.jpg$

Para los ejercicios 42-49, utilice una utilidad gráfica para encontrar evidencia numérica o gráfica para determinar los límites izquierdo y derecho de la función dada como$x$ enfoques$a$. Si la función tiene un límite a medida que se$x$ aproxima$a$, indíquelo. Si no, discuta por qué no hay límite.

42)$\lim \limits_{x \to 0}e^{e^{\frac{1}{x}}}$

43)$\lim \limits_{x \to 0}e^{e^{− \frac{1}{x^2}}}$

Contestar: $\lim \limits_{x \to 0}e^{e^{− \frac{1}{x^2}}}=1.0$

44)$\lim \limits_{x \to 0} \dfrac{|x|}{x}$

45)$\lim \limits_{x \to −1} \dfrac{|x+1|}{x+1}$

Contestar: $\lim \limits_{ x→−1^−}\dfrac{| x+1 |}{x+1}=\dfrac{−(x+1)}{(x+1)}=−1$y$\lim \limits_{ x \to −1^+}\dfrac{| x+1 |}{x+1}=\dfrac{(x+1)}{(x+1)}=1$; dado que el límite de la derecha no es igual al límite de la izquierda,$\lim \limits_{ x \to −1}\dfrac{|x+1|}{x+1}$ no existe.

46)$\lim \limits_{ x \to 5} \dfrac{| x−5 |}{5−x}$

47)$\lim \limits_{ x \to −1}\dfrac{1}{(x+1)^2}$

Contestar: $\lim \limits_{ x \to −1} \dfrac{1}{(x+1)^2}$no existe. La función aumenta sin límite a medida que$x$ se$−1$ aproxima desde cualquier lado.

48)$\lim \limits_{ x \to 1} \dfrac{1}{(x−1)^3}$

49)$\lim \limits_{ x \to 0} \dfrac{5}{1−e^{\frac{2}{x}}}$

Contestar: $\lim \limits_{ x \to 0} \dfrac{5}{1−e^{\frac{2}{x}}}$no existe. Los valores de función$5$ se acercan desde la izquierda y se acercan$0$ desde la derecha.

50) Utilizar evidencia numérica y gráfica para comparar y contrastar los límites de dos funciones cuyas fórmulas parecen similares:$f(x)=\left | \dfrac{1−x}{x} \right |$ y$g(x)=\left | \dfrac{1+x}{x} \right |$ como$x$ enfoques$0$. Utilice una utilidad gráfica, si es posible, para determinar los límites izquierdo y derecho de las funciones$f(x)$ y$g(x)$ como$x$ enfoques$0$. Si las funciones tienen un límite como$x$ aproximaciones$0$, indíquelo. Si no, discuta por qué no hay límite.

Extensiones

51) Según la Teoría de la Relatividad, la masa m m de una partícula depende de su velocidad$v$. Eso es

\[m=\dfrac{m_o}{\sqrt{1−(v^2/c^2)}} \nonumber \]

donde$m_o$ es la masa cuando la partícula está en reposo y$c$ es la velocidad de la luz. Encontrar el límite de la masa,$m$, como se$v$ acerca$c^−.$

Contestar: A través del examen de los postulados y una comprensión de la física relativista, como$v→c, m→∞. $ Llevar esto un paso más allá a la solución,\[\lim \limits_{v \to c^−}m=\lim \limits_{v \to c^−} \dfrac{m_o}{\sqrt{1−(v^2/c^2)}}=∞ \nonumber \]

52) Permitir que la velocidad de la luz$c$,, sea igual a$1.0$. Si la masa,$m$, es$1$, ¿qué ocurre a$m$ como$v \to c$? Usando los valores enumerados en la Tabla siguiente, haga una conjetura en cuanto a lo que es la masa a medida que se$v$ aproxima$1.00$.

$v$	$m$
\ (v\) ">0.5	\ (m\) ">1.15
\ (v\) ">0.9	\ (m\) ">2.29
\ (v\) ">0.95	\ (m\) ">3.20
\ (v\) ">0.99	\ (m\) ">7.09
\ (v\) ">0.999	\ (m\) ">22.36
\ (v\) ">0.99999	\ (m\) ">223.61

12.2: Encontrar límites - Propiedades de límites

Graficar una función o explorar una tabla de valores para determinar un límite puede ser engorroso y llevar mucho tiempo. Cuando es posible, es más eficiente utilizar las propiedades de los límites, que es una colección de teoremas para encontrar límites. Conocer las propiedades de los límites nos permite computar los límites directamente.

Verbal

1) Dar un ejemplo de un tipo de función$f$ cuyo límite, como$a,$ se$x$ aproxima es$f(a)$.

Responder: Si$f$ es una función polinómica, el límite de una función polinómica como$x$ enfoques siempre$a$ será$f(a)$.

2) Cuando se utiliza la sustitución directa para evaluar el límite de una función racional como$x$ enfoques$a$ y el resultado es$f(a)=\dfrac{0}{0}$, ¿significa esto que el límite de$f$ no existe?

3) ¿Qué significa decir que el límite de$f(x)$, a medida que se$x$ aproxima$c$, es indefinido?

Responder: Podría significar o bien (1) los valores de la función aumentan o disminuyen sin límite como$x$ aproximaciones$c,$ o (2) los límites izquierdo y derecho no son iguales.

Algebraico

Para los ejercicios 4-30, evaluar los límites algebraicamente.

4)$\lim \limits_{x \to 0} (3)$

5)$\lim \limits_{x \to 2} \left (\dfrac{−5x}{x^2−1} \right )$

Responder: $\dfrac{−10}{3}$

6)$\lim \limits_{x \to 2} \left (\dfrac{x^2−5x+6}{x+2} \right )$

7)$\lim \limits_{x \to 3} \left (\dfrac{x^2−9}{x−3} \right )$

Responder: $6$

8)$\lim \limits_{x \to −1} \left (\dfrac{x^2−2x−3}{x+1} \right )$

9)$\lim \limits_{x \to \frac{3}{2}} \left (\dfrac{6x^2−17x+12}{2x−3} \right )$

Responder: $\dfrac{1}{2}$

10)$\lim \limits_{ x \to −\frac{7}{2}} \left (\dfrac{8x^2+18x−35}{2x+7} \right )$

11)$\lim \limits_{ x \to 3} \left (\dfrac{x^2−9}{x−5x+6} \right )$

Responder: $6$

12)$\lim \limits_{ x \to −3} \left (\dfrac{−7x^4−21x^3}{−12x^4+108x^2} \right )$

13)$\lim \limits_{ x \to 3} \left (\dfrac{x^2+2x−3}{x−3} \right )$

Responder: no existe

14)$\lim \limits_{ h \to 0} \left (\dfrac{(3+h)^3−27}{h} \right )$

15)$\lim \limits_{ h \to 0} \left (\dfrac{(2−h)^3−8}{h} \right )$

Responder: $−12$

16)$\lim \limits_{ h \to 0} \left (\dfrac{(h+3)^2−9}{h} \right )$

17)$\lim \limits_{ h \to 0} \left (\dfrac{\sqrt{5−h}−\sqrt{5}}{h} \right )$

Responder: $−\dfrac{\sqrt{5}}{10}$

18)$\lim \limits_{ x \to 0} \left (\dfrac{\sqrt{3−x}−\sqrt{3}}{x} \right )$

19)$\lim \limits_{ x \to 9} \left (\dfrac{x^2−81}{3−x} \right )$

Responder: $−108$

20)$\lim \limits_{ x \to 1} \left (\dfrac{\sqrt{x}−x^2}{1−\sqrt{x}} \right )$

21)$\lim \limits_{ x \to 0}\left ( \dfrac{x}{\sqrt{1+2x}-1} \right )$

Responder: $1$

22)$\lim \limits_{ x \to \frac{1}{2}} \left (\dfrac{x^2−\tfrac{1}{4}}{2x−1} \right )$

23)$\lim \limits_{ x \to 4} \left (\dfrac{x^3−64}{x^2−16} \right )$

Responder: $6$

24)$\lim \limits_{ x \to 2^−} \left (\dfrac{|x−2|}{x−2} \right )$

25)$\lim \limits_{ x \to 2^+} \left (\dfrac{| x−2 |}{x−2} \right )$

Responder: $1$

26)$\lim \limits_{ x \to 2} \left (\dfrac{| x−2 |}{x−2} \right )$

27)$\lim \limits_{ x \to 4^−} \left (\dfrac{| x−4 |}{4−x} \right )$

Contestar: $1$

28)$\lim \limits_{ x \to 4^+} \left (\dfrac{| x−4 |}{4−x} \right )$

29)$\lim \limits_{ x \to 4} \left (\dfrac{| x−4 |}{4−x} \right )$

Responder: no existe

30)$\lim \limits_{ x \to 2} \left (\dfrac{−8+6x−x^2}{x−2} \right )$

Para los ejercicios 31-33, utilice la información dada para evaluar los límites:$\lim \limits_{x \to c}f(x)=3, \lim \limits_{x \to c} g(x)=5$

31)$\lim \limits_{x \to c} [ 2f(x)+\sqrt{g(x)} ]$

Responder: $6+\sqrt{5}$

32)$\lim \limits_{x \to c} [ 3f(x)+\sqrt{g(x)} ]$

33)$\lim \limits_{x \to c}\dfrac{f(x)}{g(x)}$

Responder: $\dfrac{3}{5}$

Para los ejercicios 34-43, evaluar los siguientes límites.

34)$\lim \limits_{x \to 2} \cos (πx)$

35)$\lim \limits_{x \to 2} \sin (πx)$

Responder: $0$

36)$\lim \limits_{x \to 2} \sin \left (\dfrac{π}{x} \right )$

37)$f(x)= \begin{cases} 2x^2+2x+1, && x≤0 \\ x−3, && x>0 ; \end{cases} \lim \limits_{x \to 0^+}f(x)$

Responder: $−3$

38)$f(x)= \begin{cases} 2x^2+2x+1, && x≤0 \\ x−3, && x>0 ; \end{cases} \lim \limits_{x \to 0^−} f(x)$

39)$f(x)= \begin{cases} 2x^2+2x+1, && x≤0 \\ x−3, && x>0 ; \end{cases} \lim \limits_{x \to 0}f(x)$

Responder: no existe; el límite de la derecha no es lo mismo que el límite de la izquierda.

40)$\lim \limits_{x \to 4} \dfrac{\sqrt{x+5}−3}{x−4}$

41)$\lim \limits_{x \to 2^+} (2x−〚x〛)$

Responder: $2$

42)$\lim \limits_{x \to 2} \dfrac{\sqrt{x+7}−3}{x^2−x−2}$

43)$\lim \limits_{x \to 3^+}\dfrac{x^2}{x^2−9}$

Responder: El límite no existe; el límite se acerca al infinito.

Para los ejercicios 44-53, encuentra la tasa promedio de cambio$\dfrac{f(x+h)−f(x)}{h}$.

44)$f(x)=x+1$

45)$f(x)=2x^2−1$

Responder: $4x+2h$

46)$f(x)=x^2+3x+4$

47)$f(x)=x^2+4x−100$

Responder: $2x+h+4$

48)$f(x)=3x^2+1$

49)$f(x)= \cos (x)$

Responder: $\dfrac{\cos (x+h)− \cos (x)}{h}$

50)$f(x)=2x^3−4x$

51)$f(x)=\dfrac{1}{x}$

Responder: $\dfrac{−1}{x(x+h)}$

52)$f(x)=\dfrac{1}{x^2}$

53)$f(x)=\sqrt{x}$

Responder: $\dfrac{−1}{\sqrt{x+h}+\sqrt{x}}$

Gráfica

54) Encuentra una ecuación que podría ser representada por la Figura a continuación.

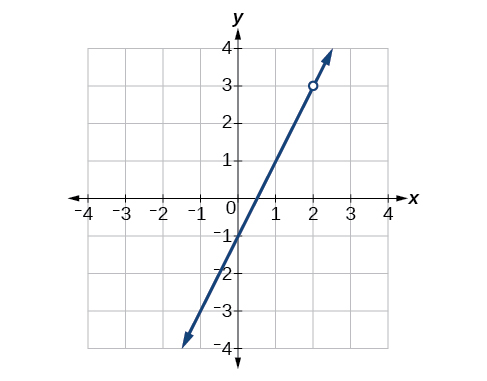
Responder: $f(x)=\dfrac{x^2+5x+6}{x+3}$

Para los ejercicios 56-57, refiérase a la Figura a continuación.

56) ¿Cuál es el límite derecho de la función a medida que se$x$ aproxima$0$?

57) ¿Cuál es el límite izquierdo de la función a medida que se$x$ aproxima$0$?

Responder: no existe

Aplicaciones del mundo real

58) La función de posición$s(t)=−16t^2+144t$ da la posición de un proyectil en función del tiempo. Encuentra la velocidad promedio (tasa promedio de cambio) en el intervalo$[ 1,2 ]$.

59) La altura de un proyectil viene dada por$s(t)=−64t^2+192t$ Encuentra la tasa promedio de cambio de la altura de$t=1$ segundo a$t=1.5$ segundos.

Responder: $52$

60) La cantidad de dinero en una cuenta después de$t$ años compuestos continuamente a$4.25\%$ intereses viene dada por la fórmula$A=A_0e^{0.0425t}$, donde$A_0$ está la cantidad inicial invertida. Encuentra la tasa promedio de cambio del saldo de la cuenta de$t=1$ año a$t=2$ años si el monto inicial invertido es$\$1,000.00.$

12.3: Continuidad

Una función que permanece nivelada durante un intervalo y luego salta instantáneamente a un valor más alto se llama función paso a paso. Esta función es un ejemplo. Una función que tiene algún agujero o rotura en su gráfica se conoce como una función discontinua. Una función escalonada, como los cargos de estacionamiento-garaje en función de las horas estacionadas, es un ejemplo de una función discontinua. Podemos verificar tres condiciones diferentes para decidir si una función es continua en un número determinado.

Verbal

1) Indicar en sus propias palabras lo que significa que una función$f$ sea continua en$x=c$.

Responder: Informalmente, si una función es continua en$x=c$, entonces no hay interrupción en la gráfica de la función at$f(c)$, y$f(c)$ se define.

2) Indique en sus propias palabras lo que significa que una función sea continua en el intervalo$(a,b)$.

Algebraico

Para los ejercicios 3-22, determinar por qué la función$f$ es discontinua en un punto$a$ dado de la gráfica. Estado qué condición falla.

3)$f(x)=\ln | x+3 |,a=−3$

Responder: discontinuo en$a=−3$;$f(−3)$ no existe

4)$f(x)= \ln | 5x−2 |,a=\dfrac{2}{5}$

5)$f(x)=\dfrac{x^2−16}{x+4},a=−4$

Responder: discontinuidad removible en no$a=−4; f(−4)$ está definida

6)$f(x)=\dfrac{x^2−16x}{x},a=0$

7)$f(x)= \begin{cases} x, && x≠3 \\ 2x, && x=3 \end{cases} a=3$

Responder: Discontinuo en$a=3; \lim \limits_{x \to 3} f(x)=3,$ pero$f(3)=6,$ que no es igual al límite.

8)$f(x) = \begin{cases} 5, &&x≠0 \\ 3, && x=0 \end{cases} a=0$

9)$f(x)= \begin{cases} \dfrac{1}{2−x}, && x≠2 \\ 3, &&x=2 \end{cases} a=2$

Responder: $\lim \limits_{x \to 2}f(x)$no existe.

10)$f(x)= \begin{cases} \dfrac{1}{x+6}, && x=−6 \\ x^2, && x≠−6 \end{cases} a=−6$

11)$f(x)=\begin{cases} 3+x, &&x<1 \\ x, &&x=1 \\ x^2, && x>1 \end{cases} a=1$

Responder: $\lim \limits_{x \to 1^−}f(x)=4;\lim \limits_{x \to 1^+}f(x)=1.$Por lo tanto,$\lim \limits_{x \to 1}f(x)$ no existe.

12)$f(x)= \begin{cases} 3−x, && x<1 \\ x, && x=1 \\ 2x^2, && x>1 \end{cases} a=1$

13)$f(x)= \begin{cases} 3+2x, && x<1 \\ x, && x=1 \\ −x^2, && x>1 \end{cases} a=1$

Responder: $\lim \limits_{x \to 1^−} f(x)=5≠ \lim \limits_{x \to 1^+}f(x)=−1$. Por lo tanto,$\lim \limits_{x \to 1}f(x)$ no existe.

14)$f(x)= \begin{cases} x^2, &&x<−2 \\ 2x+1, && x=−2 \\ x^3, && x>−2 \end{cases} a=−2$

15)$f(x)= \begin{cases} \dfrac{x^2−9}{x+3}, && x<−3 \\ x−9, && x=−3 \\ \dfrac{1}{x}, && x>−3 \end{cases} a=−3$

Responder

$\lim \limits_{x to −3^+}f(x)=−\dfrac{1}{3}$

Por lo tanto,$\lim \limits_{x \to −3} f(x)$ no existe.

16)$f(x)= \begin{cases} \dfrac{x^2−9}{x+3}, && x<−3 \\ x−9, && x=−3\\ −6, && x>−3 \end{cases} a=3$

17)$f(x)=\dfrac{x^2−4}{x−2}, a=2$

Responder: $f(2)$no está definido.

18)$f(x)=\dfrac{25−x^2}{x^2−10x+25}, a=5$

19)$f(x)=\dfrac{x^3−9x}{x^2+11x+24}, a=−3$

Responder: $f(−3)$no está definido.

20)$f(x)=\dfrac{x^3−27}{x^2−3x}, a=3$

21)$f(x)=\dfrac{x}{|x|}, a=0$

Responder: $f(0)$no está definido.

22)$f(x)=\dfrac{2|x+2|}{x+2}, a=−2$

Para los ejercicios 23-35, determinar si la función dada$f$ es continua o no en todas partes. Si es continuo en todas partes se define, indicar para qué rango es continuo. Si es discontinuo, estado donde es discontinuo.

23)$f(x)=x^3−2x−15$

Responder: Continuo$(−∞,∞)$

24)$f(x)=\dfrac{x^2−2x−15}{x−5}$

25)$f(x)=2⋅3^{x+4}$

Responder: Continuo$(−∞,∞)$

26)$f(x)=− \sin (3x)$

27)$f(x)=\dfrac{|x−2|}{x^2−2x}$

Responder: Discontinuo en$x=0$ y$x=2$

28)$f(x)= \tan (x)+2$

29)$f(x)=2x+\dfrac{5}{x}$

Responder: Discontinuo en$x=0$

30)$f(x)=\log _2 (x)$

31)$f(x)= \ln x^2 $

Responder: Continuo$(0,∞)$

32)$f(x)=e^{2x}$

33)$f(x)=\sqrt{x−4}$

Responder: Continuo$[4,∞)$

34)$f(x)= \sec (x)−3$

35)$f(x)=x^2+ \sin (x)$

Responder: Continuo encendido$(−∞,∞)$.

36) Determinar los valores de$b$ y$c$ tal que la siguiente función sea continua en toda la línea numérica real.

\[f(x)= \begin{cases}x+1, && 1<x<3 \\ x^2+bx+c, &&|x−2|≥1 \end{cases} \nonumber \]

Gráfica

Para los ejercicios 37-39, refiérase a la Figura a continuación. Cada cuadrado representa una unidad cuadrada. Para cada valor de$a$, determinar en cuál de las tres condiciones de continuidad se satisfacen$x=a$ y cuáles no.

37)$x=−3$

Responder: $1$, pero no$2$ o$3$

38)$x=2$

39)$x=4$

Responder: $1$y$2$, pero no$3$

Para los ejercicios 40-43, utilice una utilidad gráfica para graficar la función$f(x)= \sin \left (\dfrac{12π}{x} \right )$ como en la Figura. Establezca el$x$ eje a una corta distancia antes y después$0$ para ilustrar el punto de discontinuidad.

40) ¿Qué condiciones de continuidad fallan en el punto de discontinuidad?

41) Evaluar$f(0)$.

Responder: $f(0)$está indefinido.

42) Resolver por$x$ si$f(x)=0$.

43) ¿Cuál es el dominio$f(x)$?

Responder: $(−∞,0)∪(0,∞)$

Para los ejercicios 44-45, considere la función que se muestra en la Figura a continuación.

44)$x$ ¿En qué coordenadas es discontinua la función?

45) ¿Qué condición de continuidad se viola en estos puntos?

Responder

A$x=−1$, el límite no existe. En$x=1, f(1)$ no existe.

At$x=2$, parece haber una asíntota vertical, y el límite no existe.

46) Considerar la función que se muestra en la Figura a continuación. $x$¿En qué coordenadas es discontinua la función? ¿Qué condición (es) de continuidad se violaron?

47) Construir una función que pase por el origen con una pendiente constante de$1$, con discontinuidades removibles en$x=−7$ y$x=1$.

Responder: $\dfrac{x^3+6x^2−7x}{(x+7)(x−1)}$

48) La función$f(x)=\dfrac{x^3−1}{x−1}$ se grafica en la siguiente figura. Parece ser continuo en el intervalo$[−3,3]$, pero hay un$x$ -valor en ese intervalo en el que la función es discontinua. Determinar el valor$x$ en el que la función es discontinua, y explicar el escollo de utilizar la tecnología al considerar la continuidad de una función examinando su gráfica.

49) Encuentra el límite$\lim \limits_{ x \to 1}f(x)$ y determina si la siguiente función es continua en$x=1$:

\[fx= \begin{cases} x^2+4 && x≠1 \\ 2 && x=1\end{cases} \nonumber \]

Responder: La función es discontinua en$x=1$ porque el límite a medida que$1$ se$x$ acerca es$5$ y$f(1)=2$.

50) La gráfica de$f(x)= \dfrac{\sin (2x)}{x}$ se muestra en la siguiente figura. ¿La función es$f(x)$ continua en$x=0?$ Por qué o por qué no?

12.4: Derivados

El cambio dividido por el tiempo es un ejemplo de una tasa. Las tasas de cambio en los ejemplos anteriores son diferentes cada una. En otras palabras, algunos cambiaron más rápido que otros. Si tuviéramos que graficar las funciones, podríamos comparar las tasas determinando las pendientes de las gráficas.

Verbal

1) ¿Cómo es similar la pendiente de una función lineal a la derivada?

Responder: La pendiente de una función lineal permanece igual. La derivada de una función general varía según$x$. Tanto la pendiente de una línea como la derivada en un punto miden la tasa de cambio de la función.

2) ¿Cuál es la diferencia entre la tasa promedio de cambio de una función en el intervalo$[x,x+h]$ y la derivada de la función a$x$?

3) Un automóvil recorrió$110$ millas durante el periodo de tiempo de 2:00 p.m. a 4:00 p.m. ¿Cuál fue la velocidad promedio del automóvil? Exactamente a las 2:30 P.M., la velocidad del automóvil se registró exactamente$62$ millas por hora. ¿Cuál es otro nombre para la velocidad del auto a las 2:30 P.M.? ¿Por qué esta velocidad difiere de la velocidad promedio?

Responder: La velocidad promedio es de$55$ millas por hora. La velocidad instantánea a las 2:30 p.m. es$62$ millas por hora. La velocidad instantánea mide la velocidad del automóvil en un instante de tiempo, mientras que la velocidad promedio da la velocidad del automóvil a lo largo de un intervalo.

4) Explicar el concepto de la pendiente de una curva en punto$x$.

5) Supongamos que el agua fluye hacia un tanque a una tasa promedio de$45$ galones por minuto. Traducir este enunciado al lenguaje de las matemáticas.

Responder: La tasa promedio de cambio de la cantidad de agua en el tanque es de$45$ galones por minuto. Si$f(x)$ es la función que da la cantidad de agua en el tanque en cualquier momento$t$, entonces la tasa promedio de cambio de$f(x)$ entre$t=a$ y$t=b$ es$f(a)+45(b−a)$.

Algebraico

Para los ejercicios 6-17, utilice la definición de derivada$\lim \limits_{ h \to 0}\dfrac{f(x+h)-f(x)}{h}$ para calcular la derivada de cada función.

6)$f(x)=3x-4$

7)$f(x)=-2x+1$

Responder: $f'(x)=-2$

8)$f(x)=x^2-2x+1$

9)$f(x)=2x^2+x-3$

Responder: $f'(x)=4x+1$

10)$f(x)=2x^2+5$

11)$f(x)=\dfrac{-1}{x-2}$

Responder: $f'(x)=\dfrac{1}{(x-2)^2}$

12)$f(x)=\dfrac{2+x}{1-x}$

13)$f(x)=\dfrac{5-2x}{3+2x}$

Responder: $\dfrac{-16}{(3+2x)^2}$

14)$f(x)=\sqrt{1+3x}$

15)$f(x)=3x^3-x^2+2x+5$

Responder: $f'(x)=9x^2-2x+2$

16)$f(x)=5$

17)$f(x)=5\pi$

Responder: $f'(x)=0$

Para los ejercicios 18-21, encuentra la tasa promedio de cambio entre los dos puntos.

18)$(-2,0)$ y$(-4,5)$

19)$(4,-3)$ y$(-2,-1)$

Responder: $-\dfrac{1}{3}$

20)$(0,5)$ y$(6,5)$

21)$(7,-2)$ y$(7,10)$

Responder: undefined

Para las funciones polinómicas 22-25, encuentra las derivadas.

22)$f(x)=x^3+1$

23)$f(x)=-3x^2-7x=6$

Responder: $f'(x)=-6x-7$

24)$f(x)=7x^2$

25)$f(x)=3x^3+2x^2+x-26$

Responder: $f'(x)=9x^2+4x+1$

Para las funciones 26-28, encuentre la ecuación de la línea tangente a la curva en el punto$x$ dado de la curva.

26)$f(x)=2x^2-3x\; \; x=3$

27)$f(x)=x^2+1\; \; x=2$

Responder: $y=12x-15$

28)$f(x)=\sqrt{x}\; \; x=9$

29) Para el siguiente ejercicio, encuentra$k$ tal que la línea dada sea tangente a la gráfica de la función.

\[f(x)=x^2-kx\; \; y=4x-9 \nonumber \]

Responder: $k=-10$o$k=2$

Gráfica

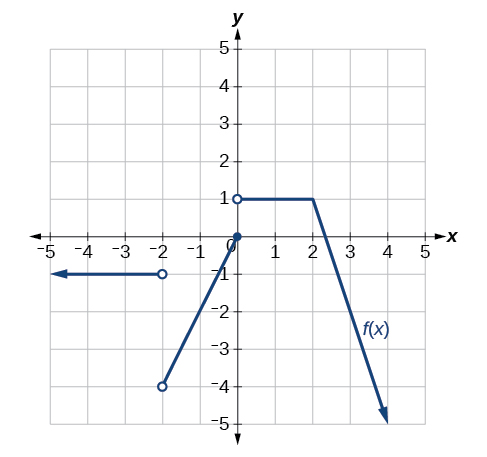
Para los ejercicios 30-33, considere la gráfica de la función$f$ y determine dónde la función es continua/discontinua y diferenciable/no diferenciable.

30)

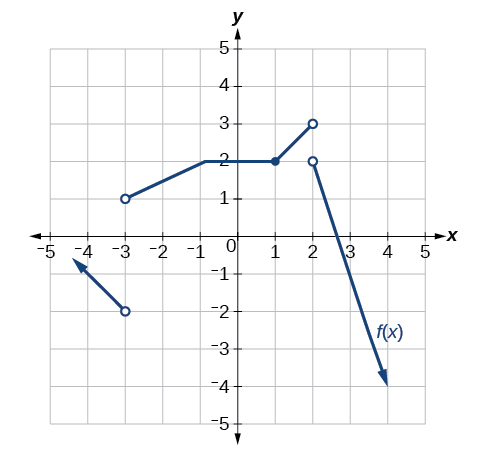
$Ex 12.4.30.png$

31)

$Ex 12.4.31.png$

Responder: Discontinuo en$x=-2$ y$x=0$. No diferenciable en$-2, 0, 2$.

32)

$Ex 12.4.32.png$

33)

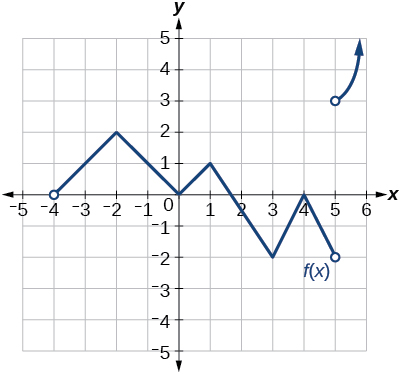
$Ex 12.4.33.png$

Responder: Discontinuo en$x=5$. No diferenciable en$-4, -2, 0, 1, 3, 4, 5$.

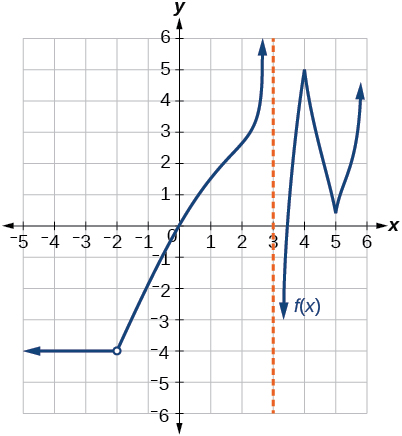
Para los ejercicios 34-43, utilice la Figura a continuación para estimar ya sea la función a un valor dado de$x$ o la derivada a un valor dado de$x$, como se indica.

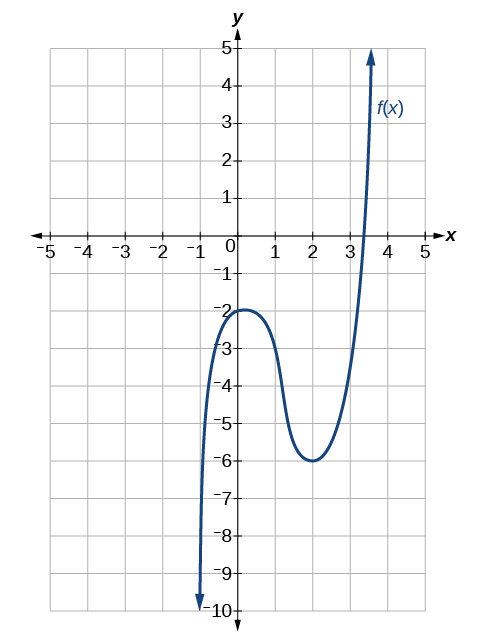
$Ex 12.4.34-43.png$

34)$f(-1)$

35)$f(0)$

Responder: $f(0)=-2$

36)$f(1)$

37)$f(2)$

Responder: $f(2)=-6$

38)$f(3)$

39)$f'(-1)$

Responder: $f'(-1)=9$

40)$f'(0)$

41)$f'(1)$

Responder: $f'(1)=-3$

42)$f'(2)$

43)$f'(3)$

Responder: $f'(3)=9$

44) Esbozar la función en base a la siguiente información:

\[f'(x)=2x, f(2)=4 \nonumber \]

Tecnología

45) Evaluar numéricamente la derivada. Explore el comportamiento de la gráfica de$f(x)=x^2$ alrededor$x=1$ graficando la función en los siguientes dominios:$[0.9,1.1], [0.99,1.01], [0.999,1.001], [0.9999, 1.0001]$. Podemos usar la función en nuestra calculadora que configura automáticamente Ymin e Ymax a los valores Xmin y Xmax que preestablecemos. (En algunas de las calculadoras gráficas de uso común, esta característica puede llamarse ZOOM FIT o ZOOM AUTO). Al examinar los valores de rango correspondientes para esta ventana de visualización, aproximar cómo cambia la curva en$x=1$, es decir, aproximar la derivada en$x=1$.

Responder: Las respuestas varían. La pendiente de la línea tangente cercana$x=1$ es$2$.

Aplicaciones del mundo real

Para los ejercicios 46-50, explicar la notación en palabras. El volumen$f(t)$ de un tanque de gasolina, en galones,$t$ minutos después del mediodía.

46)$f(0)=600$

47)$f'(30)=-20$

Responder: A las 12:30 p.m., la tasa de cambio del número de galones en el tanque es de$-20$ galones por minuto. Es decir, el tanque está perdiendo$20$ galones por minuto.

48)$f(30)=0$

49)$f'(200)=30$

Responder: $200$Minutos después del mediodía, el volumen de galones en el tanque está cambiando a razón de$30$ galones por minuto.

50)$f(240)=500$

Para los ejercicios 51-55, explique las funciones en palabras. La altura,$s$, de un proyectil después de$t$ segundos viene dada por$s(t)=-16t^2+80t$.

51)$s(2)=96$

Responder: La altura del proyectil después de$2$ segundos es de$96$ pies.

52)$s'(2)=16$

53)$s(3)=96$

Responder: La altura del proyectil a los$t=3$ segundos es de$96$ pies.

54)$s'(3)=-16$

55)$s(0)=0, s(5)=0$

Responder: La altura del proyectil es cero en$t=0$ y otra vez en$t=5$. Es decir, el proyectil inicia en el suelo y vuelve a caer a la tierra después de$5$ segundos.

Para los ejercicios 56-57, el volumen$V$ de una esfera con respecto a su radio$r$ viene dado por$V=\dfrac{4}{3}\pi r^3$.

56) Encuentra la tasa promedio de cambio de$V$ como$r$ cambios de$1$$2$ cm a cm.

57) Encuentra la tasa instantánea de cambio de$V$ cuando$r=3$ cm.

Responder: $36\pi $

Para los ejercicios 58-60, los ingresos generados por la venta de$x$ artículos son dados por$R(x)=2x^2+10x$.

58) Encontrar el cambio promedio de la función de ingresos como$x$ cambios de$x=10$ a$x=20$.

59) Encontrar$R'(10)$ e interpretar.

Responder: $\$50.00$por unidad, que es la tasa instantánea de cambio de ingresos cuando se venden exactamente$10$ unidades.

60) Encontrar$R'(15)$ e interpretar. Comparar$R'(15)$ con$R'(10)$, y explicar la diferencia.

Para los ejercicios 61-63, el costo de producción de$x$ celulares es descrito por la función$C(x)=x^2-4x+1000$.

61) Encontrar la tasa promedio de cambio en el costo total a medida que$x$ cambia de$x=10$ a$x=15$.

Responder: $\$21$por unidad

62) Encontrar el costo marginal aproximado, cuando se han producido$15$ celulares, de producir el$16^{th}$ celular.

63) Encontrar el costo marginal aproximado, cuando se han producido$20$ celulares, de producir el$21^{st}$ celular.

Responder: $\$36$

Extensión

Para los ejercicios 64-67, utilizar la definición para la derivada en un punto$x=a$,$\lim \limits_{x \to a}\dfrac{f(x)-f(a)}{x-a}$, para encontrar la derivada de las funciones.

64)$f(x)=\dfrac{1}{x^2}$

65)$f(x)=5x^2-x+4$

Responder: $f'(x)=10a-1$

66)$f(x)=-x^2+4x+7$

67)$f(x)=\dfrac{-4}{3-x^2}$

Responder: $\dfrac{4}{(3-x)^2}$

Colaboradores y Atribuciones

Template:OpenStaxPreCalc