22.1: Introducción a los vectores
- Page ID
- 117786
Hay otra manera de discutir el plano\(2\) -dimensional, que resalta algunas otras propiedades útiles del plano\(\mathbb{R}^2\). Esta es la noción de\(\mathbb{R}^2\) como espacio vectorial. Comenzamos definiendo vectores en el plano.
Un vector geométrico en el plano es un objeto geométrico en el plano\(\mathbb{R}^2\) que viene dado por una dirección y magnitud. Denotamos un vector por\(\vec{v}\) (es escrito por algunos autores como v), su magnitud se denota por\(||\vec{v}||\), y su ángulo direccional por\(\theta\).
Los vectores suelen estar representados por segmentos de línea dirigidos\(\vec{v}=\overrightarrow{PQ}\), donde dos segmentos de línea representan el mismo vector, si uno puede moverse al otro por traslación paralela (sin cambiar su dirección o magnitud).
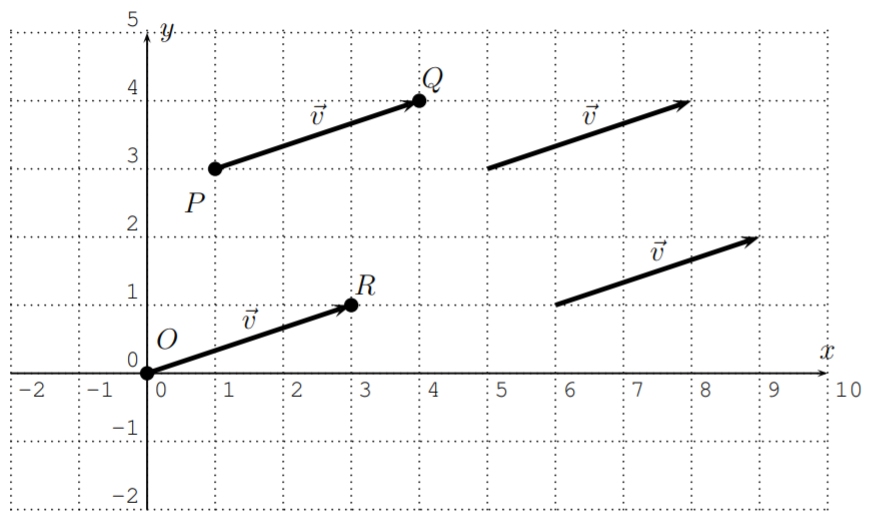
En particular, siempre podemos representar un vector\(\vec{v}\)\(\overrightarrow{OR}\) disponiendo el punto de partida de\(\vec{v}\) al origen\(O(0,0)\). Si\(R\) se da en coordenadas por\(R(a,b)\), entonces también escribimos para\(\vec{v}=\overrightarrow{OR}\),
\[\boxed{\vec{v}=\langle a,b\rangle} \quad\text{ or, alternatively, }\quad \boxed{\vec{v}=\begin{bmatrix} a \\ b \end{bmatrix}} \nonumber \]
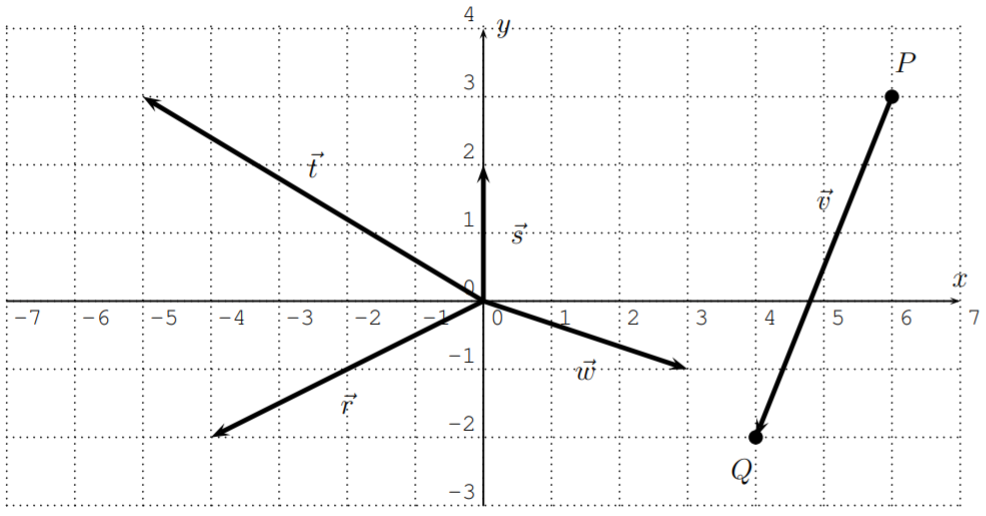
Grafica los vectores\(\vec{v}, \vec{w}, \vec{r}, \vec{s}, \vec{t}\) en el plano, donde\(\vec{v}=\overrightarrow{PQ}\) con\(P(6,3)\) y\(Q(4,-2)\), y
\[\vec{w}=\langle 3, -1\rangle, \quad \vec{r}=\langle -4, -2\rangle, \quad \vec{s}=\langle 0, 2\rangle, \quad \vec{t}=\langle -5, 3\rangle \nonumber \]
Solución
Las fórmulas para la magnitud y el ángulo direccional de un vector se pueden obtener precisamente de la misma manera que el valor absoluto y el ángulo de un número complejo. A partir de la ecuación 21.1.3 en Observación [obs:Polar-form], se obtienen las siguientes fórmulas análogas.
Dejar\(\vec{v}=\langle a,b\rangle\) ser un vector en el plano\(\mathbb{R}^2\). Entonces la magnitud y el ángulo de\(\vec{v}\) están dados por:
\[\label{EQU:magnitude-and-angle} \boxed{ ||\vec{v}||=\sqrt{a^2+b^2} } \quad \text{ and } \quad \boxed{\tan(\theta)=\dfrac{b}{a}}\]
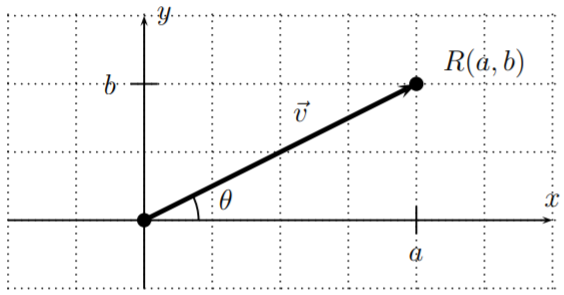
Por el contrario, podemos recuperar las coordenadas de un vector\(\vec{v}\) a partir de su magnitud\(||\vec{v}||\) y ángulo\(\theta\) por (ver ecuación 21.1.1 de la página):
\[\label{EQU:magnitude-angle-to-component} \boxed{ \vec{v}=\langle \,\,\, ||\vec{v}||\cdot \cos(\theta)\,\,\, , \,\,\, ||\vec{v}||\cdot \sin(\theta) \,\,\, \rangle}\]
Encuentra la magnitud y el ángulo direccional de los vectores dados.
- \(\langle -6,6\rangle\)
- \(\langle 4,-3\rangle\)
- \(\langle -2\sqrt{3},-2\rangle\)
- \(\langle 8, 4\sqrt{5} \rangle\)
- \(\overrightarrow{PQ}\), donde\(P(9,2)\) y\(Q(3,10)\)
Solución
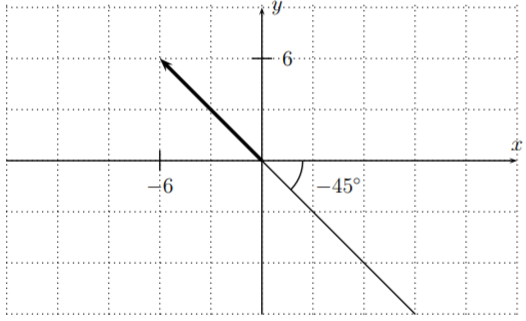
- Usamos fórmulas\(\ref{EQU:magnitude-and-angle}\), y el cálculo es en analogía con el Ejemplo 21.1.3. La magnitud de\(\vec{v}=\langle -6,6\rangle\) es
\[||\vec{v}||=\sqrt{(-6)^2+6^2}=\sqrt{36+36}=\sqrt{72}=\sqrt{36\cdot 2}=6\sqrt{2} \nonumber \]
El ángulo direccional\(\theta\) viene dado por\(\tan(\theta)=\dfrac{6}{-6}=-1\). Ahora, ya que\(\tan^{-1}(-1)=-\tan^{-1}(1)=-45^\circ\) está en el cuarto cuadrante, pero\(\vec{v}=\langle -6,6\rangle\) dibujado en el origen\(O(0,0)\) tiene su punto final en el segundo cuadrante, vemos que el ángulo\(\theta=-45^\circ+180^\circ=135^\circ\).
- La magnitud de\(\vec{v}=\langle4,-3\rangle\) es
\[||\vec{v}||=\sqrt{4^2+(-3)^2}=\sqrt{16+9}=\sqrt{25}=5 \nonumber \]
El ángulo direccional viene dado por\(\tan(\theta)=\dfrac{-3}{4}\). Ya que\(\tan^{-1}\left(\dfrac{-3}{4}\right)\approx -36.9^\circ\) está en el cuarto cuadrante, y\(\vec{v}=\langle4,-3\rangle\) está en el cuarto cuadrante, vemos que
\[\theta=\tan^{-1}\left(\dfrac{-3}{4}\right)\approx -36.9^\circ \nonumber \]
- La magnitud de\(\vec{v}=\langle -2\sqrt{3},-2\rangle\) es
\[||\vec{v}||=\sqrt{(-2\sqrt{3})^2+(-2)^2}=\sqrt{4\cdot 3+4}=\sqrt{12+4}=\sqrt{16}=4 \nonumber \]
El ángulo direccional viene dado por\(\tan(\theta)=\dfrac{-2}{-2\sqrt{3}}=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3}\). Ahora,\(\tan^{-1}\left(\dfrac{\sqrt{3}}{3}\right)=30^\circ=\dfrac{\pi}{6}\) está en el primer cuadrante, mientras que\(\vec{v}=\langle -2\sqrt{3},-2\rangle\) está en el tercer cuadrante. Por lo tanto, el ángulo se da agregando un adicional\(\pi\) al ángulo.
\[\theta=\pi+\dfrac{\pi}{6}+\dfrac{6\pi+\pi}{6}=\dfrac{7\pi}{6} \nonumber \]
- La magnitud de\(\vec{v}=\langle 8, 4\sqrt{5} \rangle\) es
\[||\vec{v}||=\sqrt{8^2+(4\sqrt{5})^2}=\sqrt{64+16\cdot 5}=\sqrt{64+80}=\sqrt{144}=12 \nonumber \]
El ángulo direccional viene dado por la ecuación\(\tan(\theta)=\dfrac{4\sqrt{5}}{8}=\dfrac{\sqrt{5}}{2}\). Dado que ambos\(\tan^{-1}\left(\dfrac{\sqrt{5}}{2}\right)\approx 48.2^\circ\) y el punto final de\(\vec{v}\) (representado con punto inicial en el origen) están en el primer cuadrante, tenemos:
\[\theta=\tan^{-1}\left(\dfrac{\sqrt{5}}{2}\right)\approx 48.2^\circ \nonumber\]
- Primero necesitamos encontrar el vector\(\vec{v}=\overrightarrow{PQ}\) en la forma\(\vec{v}=\langle a,b \rangle\). El vector en el siguiente plano muestra que\(\vec{v}\) viene dado por\[\vec{v}=\langle 3-9, 10-2 \rangle =\langle -6,8 \rangle \nonumber \]
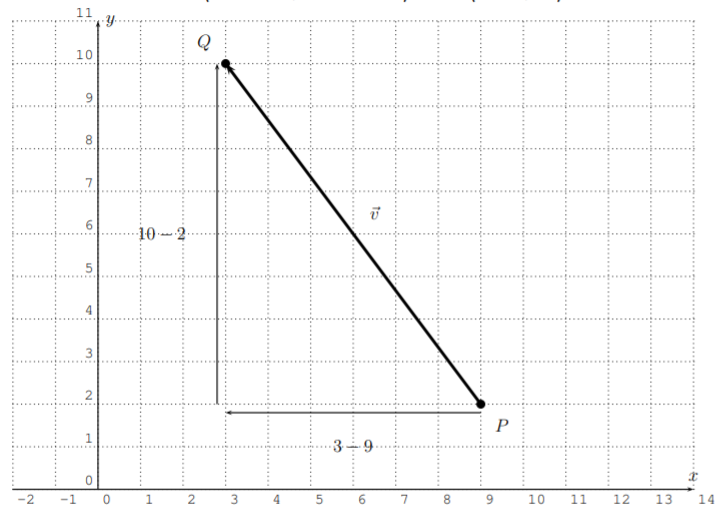
A partir de esto calculamos la magnitud a ser
\[||\vec{v}|| = \sqrt{(-6)^2+8^2}=\sqrt{36+64}=\sqrt{100}=10 \nonumber \]
El ángulo direccional viene dado por\(\tan(\theta)=\dfrac{8}{-6}=-\dfrac{4}{3}\). Ahora,\(\tan^{-1}\left(-\dfrac{4}{3}\right)\approx -53.1^\circ\) está en el cuadrante IV, mientras que\(\vec{v}=\langle-6,8\rangle\) tiene un punto final en el cuadrante II (cuando se representa\(\vec{v}\) con punto de partida en el origen\(O(0,0)\)). Por lo tanto, el ángulo direccional es
\[\theta=180^\circ+\tan^{-1}\left(-\dfrac{4}{3}\right)\approx 126.9^\circ \nonumber\]


