22.2: Operaciones sobre vectores

Hay dos operaciones básicas sobre vectores, que son la multiplicación escalar y la suma de vectores. Comenzamos con la multiplicación escalar.

Definición: Multiplicación escalar

La multiplicación escalar de un número real\(r\) con un vector\(\vec{v}=\langle a,b\rangle\) se define como el vector dado multiplicando\(r\) a cada coordenada.

\[\boxed{ r\cdot \langle a,b \rangle := \langle r\cdot a, r \cdot b \rangle }\]

Estudiamos el efecto de la multiplicación escalar con un ejemplo.

Ejemplo\(\PageIndex{1}\)

Multiplicar y graficar los vectores.

1. \(4\cdot \langle-2,1\rangle\)
2. \((-3)\cdot \langle -6,-2 \rangle\)

Solución

1. El cálculo es sencillo.

\[4\cdot \langle-2,1\rangle=\langle4\cdot (-2),4\cdot 1\rangle=\langle-8,4\rangle \nonumber \]

Los vectores se muestran a continuación. Vemos, eso\(\langle-2,1\rangle\) y\(\langle-8,4\rangle\) ambos tienen el mismo ángulo direccional, y este último estira el primero por un factor\(4\).

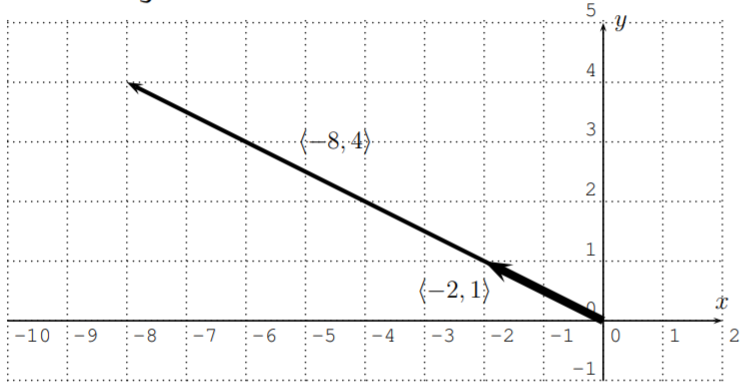
2. Álgebraicamente, calculamos la multiplicación escalar de la siguiente manera:

\[(-3)\cdot \langle -6,-2 \rangle= \langle (-3)\cdot(-6),(-3)\cdot(-2) \rangle =\langle 18,6 \rangle \nonumber \]

Además, graficar los vectores da:

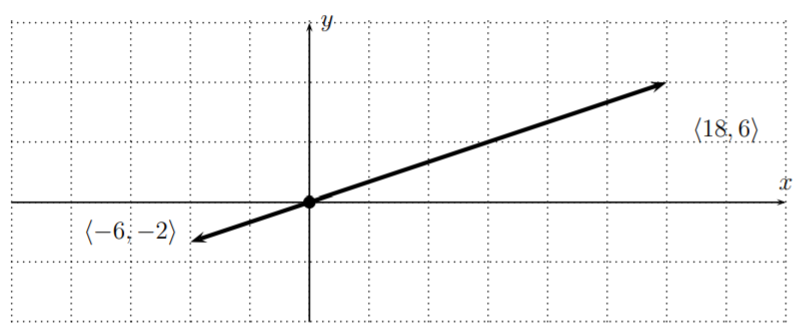
Vemos que el ángulo direccional de los dos vectores difiere en\(180^\circ\). En efecto,\(\langle18,6\rangle\) se obtiene de\(\langle -6,-2\rangle\) reflejándolo en el origen\(O(0,0)\) y luego estirando el resultado por un factor\(3\).

Vemos del ejemplo anterior, que la multiplicación escalar por un número positivo\(c\) no cambia el ángulo del vector, sino que multiplica la magnitud por\(c\).

Observación: c-veces-vector

Dejar\(\vec{v}\) ser un vector con magnitud\(||\vec{v}||\) y ángulo\(\theta_{\vec{v}}\). Entonces, para un escalar positivo,\(r>0\), el múltiplo escalar\(r\cdot \vec{v}\) tiene el mismo ángulo que\(\vec{v}\), y una magnitud que es\(r\) por la magnitud de\(\vec{v}\):

\[\text{for $r>0$: } \quad ||r\cdot \vec{v}|| = r\cdot ||\vec{v}|| \quad\text{ and } \quad \theta_{r\cdot \vec{v}}=\theta_{\vec{v}}\]

Definición: Vector de unidad

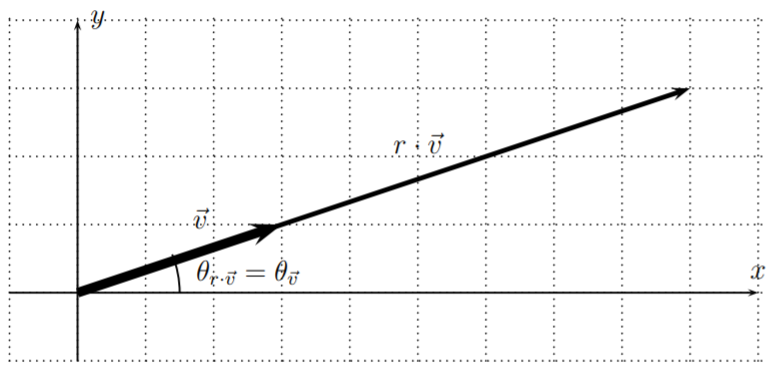
Un vector\(\vec{u}\) se llama vector unitario, si tiene una magnitud de\(1\).

\[\vec{u} \text{ is a unit vector } \quad \iff \quad ||\vec{u}||=1\]

Hay dos vectores unitarios especiales, que son los vectores que apuntan en la dirección\(x\) - y la\(y\) -dirección.

\[\boxed{\vec{i}:=\langle 1,0\rangle}\quad \text{ and }\quad \boxed{\vec{j}:=\langle 0,1\rangle}\]

Ejemplo\(\PageIndex{2}\)

Encuentra un vector de unidad en la dirección de\(\vec{v}\).

1. \(\langle 8, 6 \rangle\)
2. \(\langle -2,3\sqrt{7} \rangle\)

Solución

1. Tenga en cuenta que la magnitud de\(\vec{v}=\langle 8, 6 \rangle\) es

\[||\langle 8, 6 \rangle||=\sqrt{8^2+6^2}=\sqrt{64+36}=\sqrt{100}=10 \nonumber \]

Por lo tanto, si\(\dfrac{1}{10}\) multiplicamos\(\langle 8, 6 \rangle\) por obtenemos\(\dfrac{1}{10}\cdot \langle 8, 6 \rangle=\langle \dfrac{8}{10}, \dfrac{6}{10} \rangle=\langle \dfrac{4}{5}, \dfrac{3}{5} \rangle\), que (según la Observación [obs:C-times-vector] anterior) tiene el mismo ángulo direccional que\(\langle 8, 6 \rangle\), y tiene una magnitud de\(1\):

\[\left|\left|\dfrac{1}{10}\cdot \langle 8, 6 \rangle\right|\right| = \dfrac{1}{10}\cdot ||\langle 8, 6 \rangle||=\dfrac{1}{10}\cdot 10=1 \nonumber \]

2. La magnitud de\(\langle -2,3\sqrt{7} \rangle\) es

\[||\langle -2,3\sqrt{7} \rangle||=\sqrt{(-2)^2+(3\sqrt{7})^2}=\sqrt{4+9\cdot 7}=\sqrt{4+63}=\sqrt{67} \nonumber\]

Por lo tanto, tenemos el vector de unidad

\[\dfrac{1}{\sqrt{67}}\cdot \langle -2,3\sqrt{7} \rangle=\langle \dfrac{-2}{\sqrt{67}},\frac{3\sqrt{7} }{\sqrt{67}}\rangle=\langle \dfrac{-2\sqrt{67}}{67},\dfrac{3\sqrt{7}\sqrt{67}}{67}\rangle=\langle \dfrac{-2\sqrt{67}}{67},\dfrac{3\sqrt{469}}{67}\rangle \nonumber\]

que nuevamente tiene el mismo ángulo direccional que\(\langle -2,3\sqrt{7} \rangle\). Ahora,\(\dfrac{1}{\sqrt{67}}\cdot \langle -2,3\sqrt{7} \rangle\) es un vector unitario, ya que\[||\dfrac{1}{\sqrt{67}}\cdot \langle -2,3\sqrt{7} \rangle||=\dfrac{1}{\sqrt{67}}\cdot ||\langle -2,3\sqrt{7} \rangle||=\dfrac{1}{\sqrt{67}}\cdot \sqrt{67}=1 \nonumber \]

La segunda operación sobre vectores es la adición de vectores, que discutimos ahora.

Definición: Adición de vectores

Dejar\(\vec{v}=\langle a,b \rangle\) y\(\vec{w}=\langle c,d \rangle\) ser dos vectores. Luego, la adición vectorial\(\vec{v}+\vec{w}\) se define por la adición de componentes:

\[\boxed{\,\, \langle a,b \rangle+\langle c,d \rangle:=\langle a+c,b+d \rangle \,\,}\]

En cuanto al plano, la suma vectorial corresponde a colocar los vectores\(\vec{v}\) y\(\vec{w}\) como los bordes de un paralelogramo, de manera que\(\vec{v}+\vec{w}\) se convierte en su diagonal. Esto se muestra a continuación.

Ejemplo\(\PageIndex{3}\)

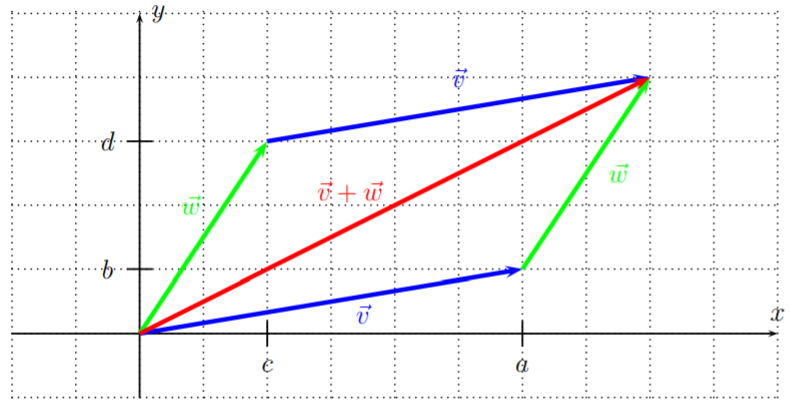
Realizar la adición de vectores y simplificar en la medida de lo posible.

1. \(\langle 3,-5 \rangle+\langle 6,4 \rangle\)
2. \(5\cdot \langle -6,2 \rangle-7\cdot \langle 1, -3 \rangle\)
3. \(4\vec{i}+9\vec{j}\)
4. Encuentra\(2\vec{v}+3\vec{w}\) para\(\vec{v}=-6\vec{i}-4\vec{j}\) y\(\vec{w}=10\vec{i}-7\vec{j}\)
5. Encuentra\(-3\vec{v}+5\vec{w}\) para\(\vec{v}=\langle 8,\sqrt{3} \rangle\) y\(\vec{w}=\langle 0,4\sqrt{3} \rangle\)

Solución

Podemos encontrar la respuesta por cómputo algebraico directo.

1. \(\langle 3,-5\rangle+\langle 6,4\rangle=\langle 3+6,-5+4\rangle=\langle 9,-1\rangle\)
2. \(5 \cdot\langle-6,2\rangle-7 \cdot\langle 1,-3\rangle=\langle-30,10\rangle+\langle-7,21\rangle=\langle-37,31\rangle\)
3. \(4 \vec{i}+9 \vec{j}=4 \cdot\langle 1,0\rangle+9 \cdot\langle 0,1\rangle=\langle 4,0\rangle+\langle 0,9\rangle=\langle 4,9\rangle\)

A partir del último cálculo, vemos que cada vector puede escribirse como una combinación lineal de los vectores\(\vec{i}\) y\(\vec{j}\).

\[\boxed{\langle a,b \rangle = a\cdot \vec{i}+b\cdot \vec{j}} \nonumber\]

Utilizaremos esta ecuación para el siguiente ejemplo (d). Aquí,\(\vec{v}=-6\vec{i}-4\vec{j}=\langle-6,-4\rangle\) y\(\vec{w}=10\vec{i}-7\vec{j}=\langle 10,-7\rangle\). Por lo tanto, obtenemos:

4. \(2 \vec{v}+3 \vec{w}=2 \cdot\langle-6,-4\rangle+3 \cdot\langle 10,-7\rangle=\langle-12,-8\rangle+\langle 30,-21\rangle=\langle 18,-29\rangle\)

5. \(\begin{aligned}-3 \vec{v}+5 \vec{w} &=-3 \cdot\langle 8, \sqrt{3}\rangle+5 \cdot\langle 0,4 \sqrt{3}\rangle\\&=\langle-24,-3 \sqrt{3}\rangle+\langle 0,20 \sqrt{3}\rangle \\&=\langle-24,17 \sqrt{3}\rangle\end{aligned}\)

Tenga en cuenta que la respuesta también podría escribirse como\(-3\vec{v}+5\vec{w}=-24\vec{i}+17\sqrt{3}\vec{j}\).

En muchas aplicaciones en las ciencias, los vectores juegan un papel importante, ya que muchas cantidades son descritas naturalmente por vectores. Ejemplos de esto en física incluyen la velocidad\(\vec{v}\), la aceleración\(\vec{a}\) y la fuerza\(\vec{F}\) aplicada a un objeto. [Exa:Adicion-de-fuerzas] Las fuerzas\(\vec{F_1}\) y\(\vec{F_2}\) se aplican a un objeto.

Ejemplo\(\PageIndex{4}\)

Encuentra la fuerza total resultante\(\vec{F}=\vec{F_1}+\vec{F_2}\). Determinar la magnitud y el ángulo direccional de la fuerza total\(\vec{F}\). Aproximar estos valores según sea necesario. Recordemos que el sistema internacional de unidades para la fuerza es el newton\([1N=1\frac{kg\cdot m}{s^2}]\).

1. \(\vec{F_1}\)tiene\(3\) newtons de magnitud, y ángulo\(\theta_1=45^\circ\),\(\vec{F_2}\) tiene\(5\) newtons de magnitud, y ángulo\(\theta_2=135^\circ\)
2. \(||\vec{F_1}||=7\)newtons, y\(\theta_1=\dfrac{\pi}{6}\), y\(||\vec{F_2}||=4\) newtons, y\(\theta_2=\dfrac{5\pi}{3}\)

Solución

1. Los vectores\(\vec{F_1}\) y\(\vec{F_2}\) están dados por sus magnitudes y ángulos direccionales. Sin embargo, la adición de vectores (en Definición [DEF:vector-adición]) se define en términos de sus componentes. Por lo tanto, nuestra primera tarea es encontrar los vectores en forma de componentes. Como se indicó en la ecuación 22.1.2 [equ:Magnitude-ángulo-a-componente] en la página, los vectores son calculados por\(\vec{v}=\langle \,\,\, ||\vec{v}||\cdot \cos(\theta)\,\,\, , \,\,\, ||\vec{v}||\cdot \sin(\theta) \,\,\, \rangle\). Por lo tanto,

\[\begin{aligned} \vec{F_1} &= \langle 3\cdot \cos(45^\circ), 3\cdot \sin(45^\circ) \rangle= \langle 3\cdot \dfrac{\sqrt{2}}{2}, 3\cdot \dfrac{\sqrt{2}}{2} \rangle= \langle \dfrac{3\sqrt{2}}{2}, \dfrac{3\sqrt{2}}{2} \rangle \\ \vec{F_2} &= \langle 5\cdot \cos(135^\circ), 5\cdot \sin(135^\circ) \rangle= \langle 5\cdot \dfrac{-\sqrt{2}}{2}, 5\cdot \dfrac{\sqrt{2}}{2} \rangle =\langle \dfrac{-5\sqrt{2}}{2}, \dfrac{5\sqrt{2}}{2} \rangle\end{aligned} \nonumber \]

La fuerza total es la suma de las fuerzas.

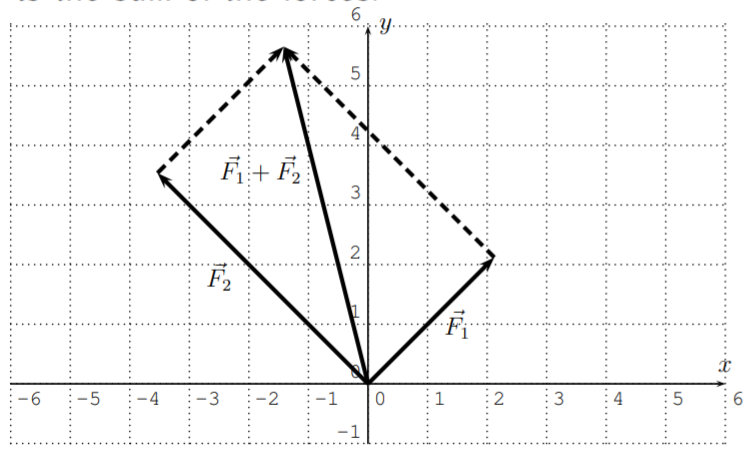
\[\begin{aligned} \vec{F}&=\vec{F_1}+\vec{F_2}\\& = \langle \dfrac{3\sqrt{2}}{2}, \dfrac{3\sqrt{2}}{2} \rangle+\langle \dfrac{-5\sqrt{2}}{2}, \dfrac{5\sqrt{2}}{2} \rangle \\ &= \langle \dfrac{3\sqrt{2}}{2}+\dfrac{-5\sqrt{2}}{2}, \dfrac{3\sqrt{2}}{2} +\dfrac{5\sqrt{2}}{2}\rangle\\& =\langle \dfrac{3\sqrt{2}-5\sqrt{2}}{2}, \dfrac{3\sqrt{2}+5\sqrt{2}}{2}\rangle \\ &= \langle \dfrac{-2\sqrt{2}}{2}, \dfrac{8\sqrt{2}}{2}\rangle\\& = \langle -\sqrt{2}, 4\sqrt{2}\rangle \end{aligned} \nonumber \]

La fuerza total aplicada en los componentes es\(\vec{F}=\langle -\sqrt{2}, 4\sqrt{2}\rangle\). Tiene una magnitud de\(||\vec{F}||=\sqrt{(-\sqrt{2})^2+(4\sqrt{2})^2}=\sqrt{2+16\cdot 2}=\sqrt{34}\approx 5.83\) newton. El ángulo direccional viene dado por\(\tan(\theta)=\dfrac{4\sqrt{2}}{-\sqrt{2}}=-4\). Ya que\(\tan^{-1}(-4)\approx -76.0^\circ\) está en el cuadrante IV, y\(\vec{F}=\langle -\sqrt{2}, 4\sqrt{2} \rangle\) está en el cuadrante II, vemos que el ángulo direccional de\(\vec{F}\) es

\[\theta=180^\circ+\tan^{-1}(-4)\approx180^\circ-76.0^\circ \approx 104^\circ \nonumber \]

2. Resolvemos este ejemplo de la misma manera que resolvimos la parte (a). Primero,\(\vec{F_1}\) y\(\vec{F_2}\) en componentes viene dado por

\[\begin{aligned} \vec{F_1} &= \langle 7\cdot \cos\Big(\dfrac{\pi}{6}\Big), 7\cdot \sin\Big(\dfrac{\pi}{6}\Big) \rangle= \langle 7\cdot \dfrac{\sqrt{3}}{2}, 7\cdot \dfrac{1}{2} \rangle= \langle \dfrac{7\sqrt{3}}{2}, \dfrac{7}{2} \rangle \\ \vec{F_2} &=\langle 4\cdot \cos\Big(\dfrac{5\pi}{3}\Big), 4\cdot \sin\Big(\dfrac{5\pi}{3}\Big) \rangle= \langle 4\cdot \dfrac{1}{2}, 4\cdot \dfrac{-\sqrt{3}}{2} \rangle= \langle 2, -2\sqrt{3} \rangle\end{aligned} \nonumber \]

Por lo tanto, la fuerza total es:

\[\begin{aligned} \vec{F}&= \vec{F_1}+\vec{F_2}\\&=\langle \dfrac{7\sqrt{3}}{2}, \dfrac{7}{2} \rangle +\langle 2, -2\sqrt{3} \rangle\\&=\langle \dfrac{7\sqrt{3}}{2}+2, \dfrac{7}{2}-2\sqrt{3} \rangle \\ &\approx \langle 8.06, 0.04 \rangle\end{aligned} \nonumber \]

La magnitud es aproximadamente

\[||\vec{F}||\approx \sqrt{(8.06)^2+(0.04)^2}\approx 8.06 \text{ newton} \nonumber \]

El ángulo direccional viene dado por\(\tan(\theta)\approx \dfrac{0.04}{8.06}\). Ya que\(\vec{F}\) está en el cuadrante I, vemos eso\(\theta\approx \tan^{-1}\left(\dfrac{0.04}{8.06}\right)\approx 0.3^\circ\).

Nota

Existe una noción abstracta de un espacio vectorial. A pesar de que no utilizamos esta estructura para otros cálculos, vamos a exponer su definición. Un espacio vectorial es un conjunto\(V\), con las siguientes estructuras y propiedades. Los elementos de\(V\) se denominan vectores, denotados por el símbolo habitual\(\vec{v}\). Para cualquier vector\(\vec{v}\) y\(\vec{w}\) hay un vector\(\vec{v}+\vec{w}\), llamado la suma del vector. Para cualquier número real\(r\) y vector\(\vec{v}\), hay un vector\(r\cdot \vec{v}\) llamado producto escalar. Estas operaciones tienen que satisfacer las siguientes propiedades.

Asociatividad:\((\vec{u}+\vec{v})+\vec{w}=\vec{u}+(\vec{v}+\vec{w})\)

Conmutatividad:\(\vec{v}+\vec{w}=\vec{w}+\vec{v}\)

Elemento cero: hay un vector\(\vec{o}\) tal que\(\vec{o}+\vec{v}=\vec{v}\) y\(\vec{v}+\vec{o}=\vec{v}\) para cada vector\(\vec{v}\)

Elemento negativo: por cada\(\vec{v}\) hay un vector\(-\vec{v}\) tal que\(\vec{v}+(-\vec{v})=\vec{o}\) y\((-\vec{v})+\vec{v}=\vec{o}\)

Distributividad (1):\(r\cdot (\vec{v}+\vec{w})=r\cdot \vec{v}+ r\cdot \vec{w}\)

Distributividad (2):\((r+ s)\cdot \vec{v}=r\cdot \vec{v}+ s\cdot \vec{v}\)

Compatibilidad escalar:\((r\cdot s)\cdot \vec{v}=r\cdot (s\cdot \vec{v})\)

Identidad:\(1\cdot \vec{v}=\vec{v}\)

Un ejemplo muy importante de un espacio vectorial es el plano\(2\) -dimensional\(V=\mathbb{R}^2\) como se discutió en este capítulo.