23.1: Introducción a las Secuencias y Series

Última actualización
Guardar como PDF

Page ID: 117660

Thomas Tradler and Holly Carley
CUNY New York City College of Technology via New York City College of Technology at CUNY Academic Works

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Definición: Word

Una secuencia es una lista ordenada de números. Escribimos una secuencia en orden de la siguiente manera:\[a_1, a_2, a_3, a_4, \dots\]

En definitiva escribimos la secuencia anterior como$\{a_n\}$ o$\{a_n\}_{n\geq 1}$.

Nota

Quizás te preguntes cómo encaja este tema en el tema general de las funciones. Alternativamente, podemos definir una secuencia$a$ para que sea una función$a: \mathbb{N} \rightarrow R$, donde el dominio es todo números naturales, y el rango$R$ es un subconjunto de los números reales o complejos. Escribimos el término$n$ th de la secuencia como$a_n=a(n)$.

Ejemplo$\PageIndex{1}$

Aquí hay algunos ejemplos de secuencias.

$4, 6, 8, 10, 12, 14, 16, 18, \dots$
$1, 3, 9, 27, 81, 243, \dots$
$+5, -5, +5, -5, +5, -5, \dots$
$1, 1, 2, 3, 5, 8, 13, 21, 34, 55, \dots$
$5, 8, -12, 4, 5.3, 7, -3, \sqrt{2}, 18, \dfrac{2}{3}, 9, \dots$

Para muchas de estas secuencias podemos encontrar reglas que describen cómo obtener los términos individuales. Por ejemplo, en (a), siempre agregamos el número fijo$2$ al número anterior para obtener el siguiente, a partir del primer término$4$. Este es un ejemplo de una secuencia aritmética, y las estudiaremos con más detalle en la sección 23.2.

En (b), comenzamos con el primer elemento$1$ y multiplicamos por el número fijo$3$ para obtener el siguiente término. Este es un ejemplo de una secuencia geométrica, y las estudiaremos con más detalle en el capítulo 24.

La secuencia en (c) alterna entre$+5$ y$-5$, a partir de$+5$. Tenga en cuenta, que podemos obtener de un término a otro multiplicando$(-1)$ por el término. Por lo tanto, este es otro ejemplo de una secuencia geométrica.

La secuencia en (d) se llama la secuencia de Fibonacci. En la secuencia de Fibonacci, cada término se calcula sumando los dos términos anteriores, comenzando por los dos primeros términos$1$ y$1$:

\[1+1=2, \quad 1+2=3, \quad 2+3=5, \quad 3+5=8, \quad 5+8=13, \quad \dots \nonumber \]

Por último, la secuencia en (e) no parece tener ninguna regla obvia por la cual se generan los términos.

En muchos casos, la secuencia viene dada por una fórmula para el término$n$ th$a_n$.

Ejemplo$\PageIndex{2}$

Considera la secuencia$\{a_n\}$ con$a_n=4n+3$. Podemos calcular los términos individuales de esta secuencia:

\ (\ begin {array} {lll}
\ text {primer término:} & a_ {1} = & 4\ cdot 1+3=7\
\\ text {segundo término:} & a_ {2} = & 4\ cdot 2+3=11\
\ texto {tercer término:} & a_ {3} = & 4\ cdot 3+3=15\
\ texto {cuarto término:} & a_ {4} = & 4\ cdot 4+3=19 \\
\ text {quinto término:} & a_ {5} = & 4\ cdot 5+3=23\\
&\ vdots &
\ end {array}\)

Así, la secuencia es:$7, 11, 15, 19, 23, 27, 31, 35, \dots$

Además, a partir de la fórmula, podemos calcular directamente un término superior, por ejemplo el término$200$ th viene dado por:

\[\quad\,\,\, 200\text{th term: }\quad\, a_{200}=\,\, 4\cdot 200+3 = 803 \nonumber \]

Ejemplo$\PageIndex{3}$

Encuentra los primeros$6$ términos de cada secuencia.

$a_n=n^2$
$a_n=\dfrac{n}{n+1}$
$a_n=(-1)^n$
$a_n=(-1)^{n+1}\cdot 2^n$

Solución

Podemos calcular fácilmente los primeros$6$ términos de$a_n=n^2$ directamente:

\[1, 4, 9, 16, 25, 36, \dots \nonumber \]

También podemos usar la calculadora para producir los términos de una secuencia. Para ello, cambiamos la calculadora del modo de función al modo de secuencia en el menú de modo (pulse$\boxed{\text{mode}}$):

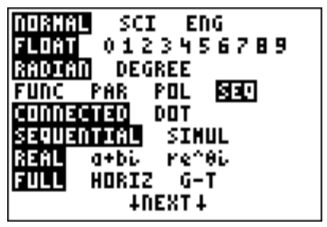
$clipboard_eee268c0e3e0887b04e6f7bc6faede85e.png$

Para ingresar a la secuencia, necesitamos usar el menú LIST (presionar$\boxed{\text{2nd}}$ y luego$\boxed{\text{stat}}$), luego ir al menú OPS (presionar$\boxed{\triangleright }$), y usar el quinto elemento (presionar$\boxed{\text{5}}$):

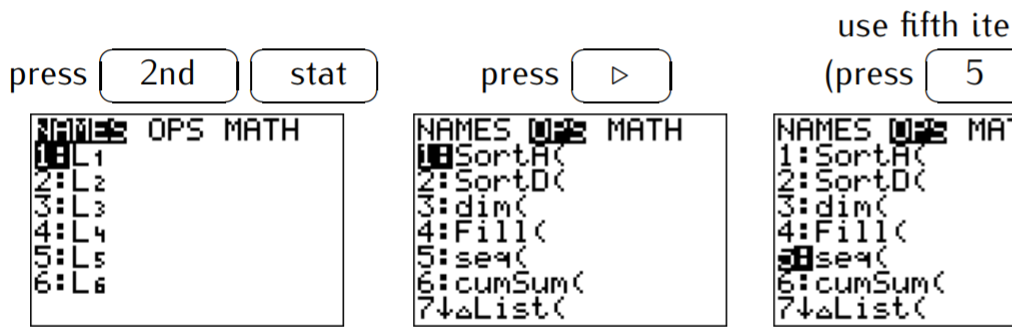
$clipboard_ece893439739ea494aff72427b4bff7e5.png$

Para la secuencia, necesitamos especificar cuatro piezas de información, donde se$n$ puede ingresar el índice a través de la$\boxed{X, T, \theta, n}$ clave.

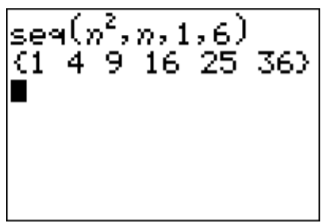
$clipboard_ed09f6dc945fac04a2c5e9f45c2a7b134.png$

La primera entrada es la fórmula dada para$a_{n}=n^{2}$

2da entrada es el índice$n$ de la secuencia$a_{n}$

Las entradas 3 y 4 son el primer y último índice 1 y 6 de la secuencia deseada, aquí:$a_{1}, \ldots, a_{6}$

Alternativamente, podemos ingresar la función en el$\boxed{y=}$ menú, comenzando desde el primer índice$n=1$, y con el término$n$ th dado por$a_n=n^2$. Los valores de la secuencia se muestran en la ventana de la tabla (pulse$\boxed{\text{2nd}}$ y$\boxed{\text{graph}}$).

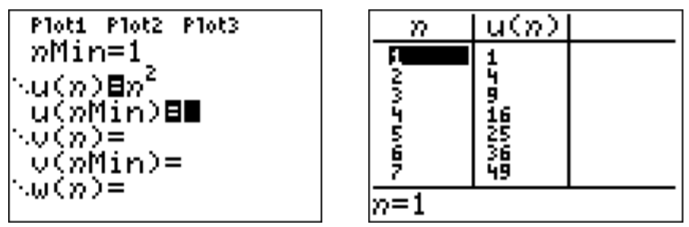
$clipboard_e41c1b4f791646e52c3569c482dbf1bf4.png$

Calculamos los términos más bajos de$a_n=\dfrac{n}{n+1}$:

\[a_1=\dfrac{1}{1+1}=\dfrac{1}{2}, \quad a_2=\dfrac{2}{2+1}=\dfrac{2}{3}, \quad a_3=\dfrac{3}{3+1}=\dfrac{3}{4}, \quad \dots \nonumber \]

Identificando el patrón, simplemente podemos escribir de la$a_1,\dots, a_6$ siguiente manera:

\[\dfrac{1}{2}, \dfrac{2}{3}, \dfrac{3}{4}, \dfrac{4}{5}, \dfrac{5}{6}, \dfrac{6}{7} \nonumber \]

También podemos usar la calculadora para encontrar la secuencia:

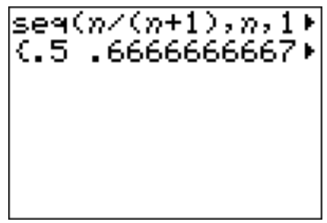
$clipboard_edea15e4998345676e40e49243a1f1228.png$

Nota

Las fracciones se pueden mostrar con la calculadora agregándole “Frac” desde el menú MATH (usando y el elemento superior). Por ejemplo, la fracción$\dfrac 2 7$ se muestra a continuación sin aproximación.

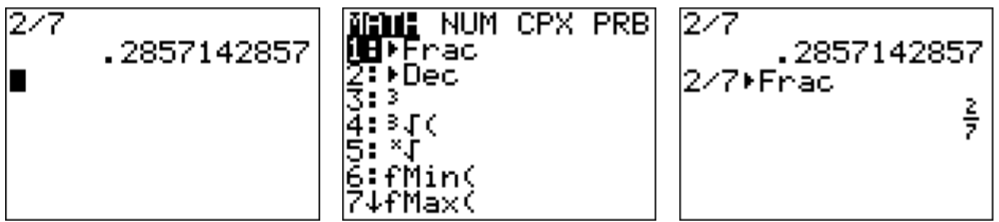
$clipboard_e21e41931af30423cc374a9987ccfd116.png$

Agregar “Frac” a la secuencia la muestra más apropiadamente como una secuencia de fracciones.

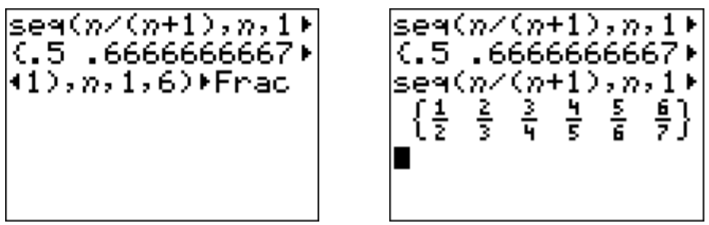
$clipboard_eebdc878f3c59439be7c67c2c32a5e84a.png$

Ya que$(-1)^n$ es$+1$ para par$n$, pero es$-1$ para impar$n$, la secuencia$a_n=(-1)^n$ es:

\[-1,+1,-1,+1,-1,+1 \nonumber \]

Similar a la parte (c),$(-1)^{n+1}$ es$-1$ para par$n$, y es$+1$ para impar$n$. Esto, junto con el cálculo$2^1=2, 2^2=4, 2^3=8, 2^4=16$, etc., obtenemos los primeros seis términos de la secuencia:

\[+2, -4, +8, -16, +32, -64 \nonumber \]

Otra forma de describir una secuencia es dando una fórmula recursiva para el término$n$ th$a_n$ en términos de los términos inferiores. Aquí hay algunos ejemplos.

Ejemplo$\PageIndex{4}$

Encuentra los primeros$6$ términos en la secuencia que se describe a continuación.

$a_1=4$, y$a_n=a_{n-1}+5$ para$n>1$
$a_1=3$, y$a_n=2\cdot a_{n-1}$ para$n>1$
$a_1=1$,$a_2=1$, y$a_n=a_{n-1}+a_{n-2}$ para$n>2$

Solución

El primer término se da explícitamente como$a_1=4$. Luego, podemos calcular los siguientes términos a través de$a_n=a_{n-1}+5$:

\[\begin{aligned} a_2 & = a_1+ 5= 4+5 =9 \\ a_3 & = a_2+ 5= 9+5 =14 \\ a_4 & = a_3+ 5= 14+5 =19 \\ a_5 & = a_4+ 5= 19+5 =24 \\ & \vdots &\end{aligned} \nonumber \]

Tenemos$a_1=3$, y calculamos$a_2=2\cdot a_1=2\cdot 3=6$$a_3=2\cdot a_2=2\cdot 6=12$,$a_4=2\cdot a_3=2\cdot 12=24$,, etc. vemos que el efecto de la relación recursiva$a_n=2\cdot a_{n-1}$ es duplicar el número anterior. La secuencia es:

\[3, 6, 12, 24, 48, 96, 192, \dots \nonumber \]

A partir de$a_1=1$, y$a_2=1$, podemos calcular los términos más altos:

\[\begin{aligned} a_3 & = a_1+ a_2= 1+1 =2 \\ a_4 & = a_2+ a_3= 1+2 =3 \\ a_5 & = a_3+ a_4= 2+3 =5 \\ a_6 & = a_4+ a_5= 3+5 =8 \\ & \vdots &\end{aligned} \nonumber \]

Al estudiar la secuencia por un corto tiempo, vemos que esta es precisamente la secuencia de Fibonacci del ejemplo 23.1.1 (d).

Nota

No hay ninguna razón específica para usar la variable de indexación$n$ en la secuencia$\{a_n\}$. En efecto, podemos usar también cualquier otra variable. Por ejemplo, si la secuencia$\{a_n\}_{n\geq 1}$ viene dada por la fórmula$a_n=4n+3$, entonces también podemos escribir esto como$a_k=4k+3$ o$a_i=4i+3$. En particular, las secuencias$\{a_n\}_{n\geq 1}=\{a_k\}_{k\geq 1}=\{a_i\}_{i\geq 1}=\{a_j\}_{j\geq 1}$ son todas idénticas a secuencias.

Nos preocuparemos por la tarea de agregar términos en una secuencia, como$a_1+a_2+a_3+\dots+a_k$, para lo cual usaremos una notación de suma estándar.

Definición: Serie

Una serie es una suma de términos en una secuencia. Denotamos la suma de los primeros$k$ términos en una secuencia con la siguiente notación:

\[\sum_{i=1}^k a_i = a_1+a_2+\dots + a_k\]

El símbolo de suma “$\sum$” proviene de la letra griega$\Sigma$, pronunciada “sigma”, que es la letra griega para “S”

Nota

De manera más general, denotamos la suma del término$j$$k$ th al th (donde$j\leq k$) en una secuencia con la siguiente noción:

\[\sum_{i=j}^k a_i = a_j+a_{j+1}+\dots + a_k \nonumber \]

Además, el término a veces también$\sum\limits_{i=j}^k a_i$ se escribe en la forma$\sum\nolimits_{i=j}^k a_i$.

Ejemplo$\PageIndex{5}$

Encuentra la suma.

$\sum_{i=1}^4 a_i, \text{ for } a_i=7i +3$
$\sum_{j=1}^6 a_j, \text{ for } a_n=(-2)^n$
$\sum_{k=1}^5 \left(4+k^2\right)$

Solución

Los primeros cuatro términos$a_1, a_2, a_3, a_4$ de la secuencia$\{a_i\}_{i\geq 1}$ son:

\[10, 17, 24, 31 \nonumber \]

Por lo tanto, la suma es:

\[\sum_{i=1}^4 a_i=a_1+a_2+a_3+a_4=10+17+24+31=82 \nonumber \]

También podemos encontrar la respuesta con la calculadora. Antes de entrar en la secuencia (vía$\boxed{\text{2nd}} \boxed{\text{stat}} \boxed{\triangleright } \boxed{\text{5}}$ como en el ejemplo 23.1.4 (a) anterior), tenemos que poner un símbolo de suma en el menú LISTA y en el submenú MATH (con$\boxed{\text{2nd}} \boxed{\text{stat}} \boxed{\triangleleft} \boxed{\text{5}}$):

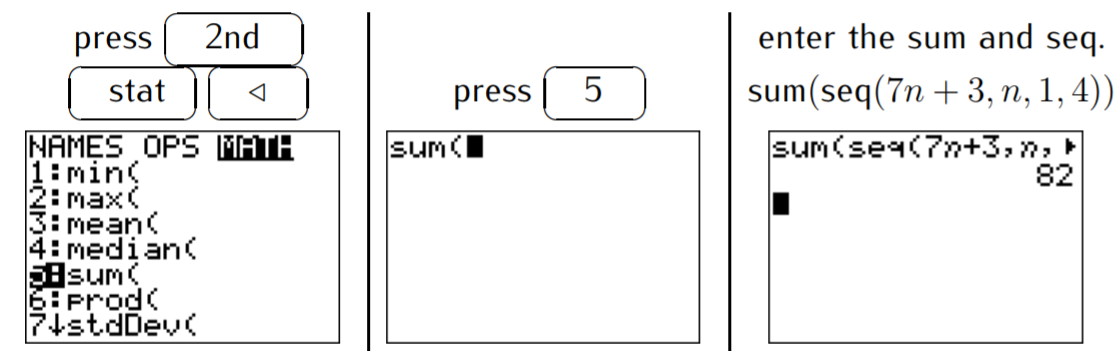
$clipboard_eb2433c494f21353b939f3d9566a462c8.png$

Los primeros seis términos de$\{a_n\}$ con$a_n=(-2)^n$ son:

\[(-2)^1=-2, \, (-2)^2=4, \,(-2)^3=-8, \, (-2)^4=16, \, (-2)^5=-32, \, (-2)^6=64 \nonumber \]

Calculamos$\sum_{j=1}^6 a_j$ sumando estos primeros seis términos. (Obsérvese que la suma es independiente del índice que$j$ aparece en la suma$\sum_{j=1}^6 a_j$, que bien podríamos sustituir por cualquier otro índice$\sum_{j=1}^6 a_j=\sum_{k=1}^6 a_k$, etc.) Obtenemos:

\[\begin{aligned} \sum_{j=1}^6 a_j &= a_1+a_2+a_3+a_4+a_5+a_6 \\ &= (-2)+4+(-8)+16+(-32)+64 = 42 \end{aligned} \nonumber \]

Para la suma$\sum_{k=1}^5 \left(4+k^2\right)$ necesitamos sumar los primeros cuatro términos de la secuencia$a_k=4+k^2$. Calculando y sumando los términos de esta secuencia, obtenemos la suma:

\[\begin{aligned} \sum_{k=1}^5 \left(4+k^2\right) &= (4+1^2)+(4+2^2)+(4+3^2)+(4+4^2)+(4+5^2) \\ &= (4+1)+(4+4)+(4+9)+(4+16)+(4+25) \\ &= 5+8+13+20+29 \\ &= 75\end{aligned} \nonumber \]

Esta respuesta, por supuesto, también se puede confirmar con la calculadora (después de reemplazar el índice$k$ por$n$) como lo hicimos en la parte (a).

Definición: Word

Nota

Ejemplo\(\PageIndex{1}\)

Ejemplo\(\PageIndex{2}\)

Ejemplo\(\PageIndex{3}\)

Nota

Ejemplo\(\PageIndex{4}\)

Nota

Definición: Serie

Nota

Ejemplo\(\PageIndex{5}\)