23.2: La secuencia aritmética

Última actualización
Guardar como PDF

Page ID: 117662

Thomas Tradler and Holly Carley
CUNY New York City College of Technology via New York City College of Technology at CUNY Academic Works

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Ya hemos encontrado ejemplos de secuencias aritméticas en la sección anterior. Una secuencia aritmética es una secuencia para la que agregamos un número constante para obtener de un término al siguiente, por ejemplo:

\[8,\underset{+3}{\hookrightarrow } 11,\underset{+3}{\hookrightarrow } 14, \underset{+3}{\hookrightarrow } 17, \underset{+3}{\hookrightarrow } 20, \underset{+3}{\hookrightarrow } 23, \dots \nonumber \]

Definición: Secuencia aritmética

Una secuencia$\{a_n\}$ se denomina secuencia aritmética si dos términos consecutivos tienen una diferencia común$d$. La secuencia aritmética está determinada por$d$ y el primer valor$a_1$. Esto se puede escribir recursivamente como:

\[a_n=a_{n-1}+d \quad \quad \text{for }n\geq 2 \nonumber \]

Alternativamente, tenemos la fórmula general para el término$n$ th de la secuencia aritmética:

\[\label{EQU:arithmetic-sequence-general-term} \boxed{a_n=a_1+d\cdot (n-1)}\]

Ejemplo$\PageIndex{1}$

Determinar si la secuencia es una secuencia aritmética. Si es así, entonces encuentra la fórmula general para$a_n$ en forma de ecuación$\ref{EQU:arithmetic-sequence-general-term}$.

$7,13, 19, 25, 31, \dots$
$13, 9, 5, 1, -3, -7, \dots$
$10, 13, 16, 20, 23, \dots$
$a_n=8\cdot n +3$

Solución

Calcular la diferencia entre dos términos consecutivos siempre da la misma respuesta$13-7=6$,,$19-13=6$$25-19=6$, etc. por lo tanto la diferencia común$d=6$, lo que demuestra que se trata de una secuencia aritmética. Además, el primer término es$a_1=7$, de manera que la fórmula general para el término$n$ th es$a_n=7+6\cdot (n-1)$.
Se comprueba que la diferencia común es$9-13=-4$,$5-9=-4$, etc., para que ésta sea una secuencia aritmética con$d=-4$. Ya que$a_1=13$, el término general es$a_n=13-4\cdot(n-1)$.
Tenemos$13-10=3$, pero$20-16=4$, para que esta no sea una secuencia aritmética.
Si escribimos el primer par de términos de$a_n=8n+3$, obtenemos la secuencia:

\[11, 19, 27, 35, 43, 51, \dots \nonumber \]

A partir de esto parece razonable sospechar que se trata de una secuencia aritmética con diferencia común$d=8$ y primer término$a_1=11$. El término general de tal secuencia aritmética es

\[a_1+d(n-1)=11+8(n-1)=11+8n-8=8n+3=a_n \nonumber \]

Esto demuestra que$a_n=8n+3=11+8(n-1)$ es una secuencia aritmética.

Ejemplo$\PageIndex{2}$

Encuentra la fórmula general de una secuencia aritmética con la propiedad dada.

$d=12$, y$a_6=68$
$a_1=-5$, y$a_{9}=27$
$a_{5}=38$, y$a_{16}=115$

Solución

De acuerdo con$\ref{EQU:arithmetic-sequence-general-term}$ la ecuación el término general es$a_n=a_1+d(n-1)$. Eso lo sabemos$d=12$, para que sólo nos falta encontrar$a_1$. Al$a_6=68$ enchufarlo$a_n=a_1+d(n-1)$, podemos resolver para$a_1$:

\[68=a_6=a_1+12\cdot (6-1)=a_1+12\cdot 5=a_1+60 \,\, \stackrel{(-60)}{\implies} \,\, a_1=68-60=8 \nonumber \]

El término$n$ th es, por lo tanto,$a_n=8+12\cdot (n-1)$.

En este caso, se nos da$a_1=-5$, pero aún necesitamos encontrar la diferencia común$d$. Al$a_9=27$ enchufarse$a_n=a_1+d(n-1)$, obtenemos

\[\begin{aligned} 27=a_9&=-5+d\cdot(9-1)\\&= -5+8d \\ \stackrel{(+5)}{\implies} 32&=8d \\ \stackrel{(\div 8)}{\implies} 4&=d \end{aligned} \nonumber \]

El término$n$ th es, por lo tanto,$a_n=-5+4\cdot (n-1)$.

En este caso no tenemos$a_1$ ni$d$. Sin embargo, las dos condiciones$a_{5}=38$ y$a_{16}=115$ dan dos ecuaciones en las dos incógnitas$a_1$ y$d$.

\ [\ left\ {\ begin {array} {c}
{3 8 = a _ {5} = a _ {1} + d (5 - 1)}\\
{1 1 5 = a _ {1} = a _ {1} + d (1 6 - 1)}
\ end {array}\ quad\ Longrightarrow\ left\ {\ begin {array} {c}
38=a_ 1} +4\ cdot d\\
115=a_ {1} +15\ cdot d
\ end {array}\ right. \ derecho. \ nonumber\]

Para resolver este sistema de ecuaciones, necesitamos recordar los métodos para hacerlo. Un método conveniente es el método de sución/resta. Para ello, restamos la ecuación superior de la inferior:

\[\begin{matrix} & 115 & = & a_1 & +15\cdot d & \\ - (& 38 & = & a_1& +4\cdot d & ) \\ \hline & 77 & = & & +11\cdot d & \\ \end{matrix} \begin{matrix} \, \\ \, \\ \quad\quad \stackrel{(\div 11)}{\implies} \quad\quad 7=d \end{matrix} \nonumber \]

La conexión$d=7$ a cualquiera de las dos ecuaciones da$a_1$. Lo conectamos a la primera ecuación$38=a_1+4d$:

\[38=a_1+4\cdot 7 \quad\implies \quad 38=a_1+28 \quad \stackrel{(-28)}{\implies} \quad 10=a_1 \nonumber \]

Por lo tanto, el término$n$ th viene dado por$a_n=10+7\cdot (n-1)$.

Podemos sumar los primeros$k$ términos de una secuencia aritmética usando un truco, que, según la tradición, fue encontrado por el matemático alemán Carl Friedrich Gauss cuando era niño en la escuela.

Ejemplo$\PageIndex{3}$

Encuentra la suma de los primeros$100$ enteros, a partir de$1$.

Solución

En otras palabras, queremos encontrar la suma de$1+2+3+\dots + 99+100$. Primero, tenga en cuenta que la secuencia$1, 2, 3, \dots$ es una secuencia aritmética. La idea principal para resolver este problema es un truco, que de hecho funcionará para cualquier secuencia aritmética:

$S=1+2+3+\cdots+98+99+100$Sea lo que queremos encontrar. Tenga en cuenta que

\[2S=\begin{array}{ccccccccccccc}&1&+&2&+&3&\cdots&+&98&+&99&+&100\\ +&100&+&99&+&98&\cdots&+&3&+&2&+&1 \end{array} \nonumber \]

Tenga en cuenta que la segunda línea también es$S$ pero se agrega en el orden inverso. Añadiendo verticalmente vemos entonces que

\[2S=101+101+101+\cdots+101+101+101, \nonumber \]

donde hay$100$ términos en el lado derecho. Entonces

\[2S=100\cdot101{\text{ and therefore }}S=\frac{100\cdot101}{2}=5050 \nonumber \]

El ejemplo anterior generaliza a la configuración más general comenzando con una secuencia aritmética arbitraria.

Observación: Secuencia aritmética

Let$\{a_n\}$ Ser una secuencia aritmética, cuyo término$n$ th viene dado por la fórmula$a_n=a_1+d(n-1)$. Entonces, la suma$a_1+a_2+\dots+a_{k-1}+a_k$ se da sumando$(a_1+a_k)$ precisamente los$\dfrac k 2$ tiempos:

\[\label{EQU:arithmetic-series} \boxed{\sum_{i=1}^k a_i =\dfrac{k}{2}\cdot (a_1+a_k)}\]

Para recordar la fórmula anterior, puede ser conveniente pensar en el lado derecho como$k\cdot\dfrac{a_1+a_k}{2}$ (esto es,$k$ multiplicado por el promedio del primer y último término).

Prueba

Para la prueba de la ecuación$\ref{EQU:arithmetic-series}$, escribimos$S= a_1+a_2+\dots +a_{k-1}+a_{k}$. Luego lo agregamos a sí mismo pero en orden inverso:

\[2S=\begin{array}{ccccccccccccc}&a_1&+&a_2&+&a_3&\cdots&+&a_{k-2}&+&a_{k-1}&+&a_k\\ +&a_{k}&+&a_{k-1}&+&a_{k-2}&\cdots&+&a_3&+&a_2&+&a_1 \end{array} \nonumber \]

Ahora tenga en cuenta que en general$a_l+a_m=2a_1+d(l+m-2)$. Vemos que sumar verticalmente da

\[2S=k(2a_1+d(k-1))=k(a_1+(a_1+d(k-1))=k(a_1+a_k) \nonumber \]

Dividir por$2$ da el resultado deseado.

Ejemplo$\PageIndex{4}$

Encuentra el valor de la serie aritmética.

Encuentra la suma$a_1+\dots +a_{60}$ de la secuencia aritmética$a_n=2+13(n-1)$.
Determinar el valor de la suma:$\sum\limits_{j=1}^{1001} (5-6j)$
Encuentra la suma de los primeros$35$ términos de la secuencia\[4, 3.5, 3, 2.5, 2, 1.5, \dots \nonumber \]

Solución

La suma viene dada por la fórmula$\ref{EQU:arithmetic-series}$:$\sum_{i=1}^k a_i=\dfrac k 2 \cdot (a_1+a_k)$. Aquí,$k=60$, y$a_1=2$ y$a_{60}=2+13\cdot(60-1)=2+13\cdot 59=2+767=769$. Obtenemos una suma de

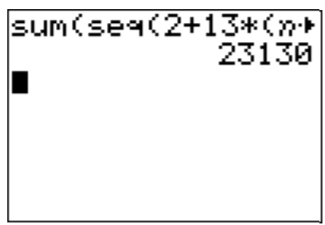
\[a_1+\dots +a_{60}=\sum_{i=1}^{60} a_i=\dfrac{60}{2}\cdot (2+769)=30\cdot 771=23130 \nonumber \]

Podemos confirmar esto con la calculadora como se describe en el ejemplo 23.1.5 en la sección anterior.

\[\text{Enter: } \operatorname{sum}(\operatorname{seq}((2+13 \cdot(n-1), n, 1,60)) \nonumber \]

$clipboard_e533312df3c127d0a2733a76c1c69cc3b.png$

Nuevamente, usamos la fórmula anterior$\sum_{j=1}^k a_j=\dfrac k 2 \cdot (a_1+a_k)$, donde la secuencia aritmética viene dada por$a_j=5-6j$ y$k=1001$. Usando los valores$a_1=5-6\cdot 1=5-6=-1$ y$a_{1001}=5-6\cdot 1001=5-6006=-6001$, obtenemos:

\[\begin{aligned} \sum_{j=1}^{1001} (5-6j)& = \dfrac{1001}{2}(a_1+a_{1001})\\&=\dfrac{1001}{2}((-1)+(-6001))\\ &= \dfrac{1001}{2}\cdot (-6002)\\& = 1001\cdot (-3001)\\& =-3004001\end{aligned} \nonumber \]

Primero tenga en cuenta que la secuencia dada$4, 3.5, 3, 2.5, 2, 1.5, \dots$ es una secuencia aritmética. Se determina por el primer término$a_1=4$ y diferencia común$d=-0.5$. El término$n$ th viene dado por$a_n=4-0.5\cdot (n-1)$, y sumando los primeros$k=35$ términos da:

\[\sum_{i=1}^{35} a_i=\dfrac{35}{2}\cdot (a_1+a_{35}) \nonumber \]

Vemos que necesitamos encontrar$a_{35}$ en la fórmula anterior:

\[a_{35}=4-0.5\cdot (35-1)=4-0.5\cdot 34=4-17=-13 \nonumber \]

Esto da una suma total de

\[\sum_{i=1}^{35} a_i=\dfrac{35}{2}\cdot (4+(-13))=\dfrac{35}{2}\cdot (-9)=\dfrac{-315}{2} \nonumber \]

La respuesta podrá escribirse como fracción o también como decimal, es decir:$\sum_{i=1}^{35}a_i=\dfrac{-315}2=-157.5$.

Definición: Secuencia aritmética

Ejemplo\(\PageIndex{1}\)

Ejemplo\(\PageIndex{2}\)

Ejemplo\(\PageIndex{3}\)

Observación: Secuencia aritmética

Ejemplo\(\PageIndex{4}\)