26.1: A.1- Funciones básicas de la calculadora

Última actualización
Guardar como PDF

Page ID: 117805

Thomas Tradler and Holly Carley
CUNY New York City College of Technology via New York City College of Technology at CUNY Academic Works

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Funciones básicas de la calculadora

En esta sección explicamos las funciones básicas de la calculadora. Hay varios botones y pantallas. A continuación describiremos aquellos que son más útiles para nosotros.

La pantalla principal

La pantalla principal es la que aparece cuando enciendes la calculadora por primera vez. Es la pantalla donde se pueden realizar operaciones como sumar números. Siempre se puede volver a la pantalla principal pulsando$\boxed{\text{2nd}}$$\boxed{\text{mode}}$. Otras pantallas se discutirán a continuación según su uso.

Los botones

Hay tres niveles de botones. Los botones físicos junto con el estampado verde y azul encima de cada botón, por ejemplo $clipboard_e4cf3f306b70972131d16dd0a932d259f.png$ . Para seleccionar los elementos en verde (azul) imprimir primero seleccione$\boxed{\text{alpha}}$ ($\boxed{\text{2nd}}$) luego el botón debajo del elemento impreso. Por ejemplo para seleccionar la letra K presione$\boxed{\text{alpha}}$ entonces$\boxed{(}$.

A partir de ahora usaremos 'botón' para significar cualquiera de los botones físicos o los pseudo-botones verdes o azules.

El botón de borrar

Siempre que quieras borrar una línea de entrada o una pantalla pulsa el$\boxed{\text{clear}}$ botón (una o dos veces).

Los botones de borrar e insertar

El botón 'DEL' ($\boxed{\text{del}}$) y el botón 'INS' ($\boxed{\text{2nd}}$$\boxed{\text{del}}$) son útiles a la hora de editar una expresión. El botón 'DEL' simplemente elimina el carácter que se encuentra en la ubicación del cursor. El botón de inserción se inserta los números o letras ingresados en la ubicación del cursor. Por ejemplo, si escribe 5+5 y se da cuenta de que quería 15+5 en su lugar, debe usar la flecha izquierda para mover el cursor a los primeros 5, presione$\boxed{\text{2nd}}$$\boxed{\text{del}}$$\boxed{\text{1}}$. ¿Qué pasa si acababas de presionar$\boxed{\text{1}}$? Tenga en cuenta que la calculadora permanece en 'modo de inserción' hasta que el cursor se mueve con el error o se presiona enter. Entonces podrías haber cambiado los primeros 5 a un 115 moviendo el cursor a los primeros 5 y presionando$\boxed{\text{2nd}}$$\boxed{\text{del}}$$\boxed{\text{1}}$$\boxed{\text{1}}$.

El botón ANS

El botón de respuesta se utiliza cuando se desea utilizar la respuesta anterior en una expresión. Por ejemplo supongamos que habías entrado$\boxed{\text{3}}$$\boxed{\text{+}}$$\boxed{\text{5}}$$\boxed{\text{enter}}$. Ahora quieres computar 7 menos el resultado de ese cómputo. Se puede presionar$\boxed{\text{7}}$$\boxed{\text{-}}$$\boxed{\text{2nd}}$$\boxed{\text{(-)}}$.

El botón ENTRADA

El botón 'ENTRADA' (la selección azul por encima de la$\boxed{\text{enter}}$ cual se ingresa presionando$\boxed{\text{2nd}}$$\boxed{\text{enter}}$) muestra la última entrada. Este es un botón particularmente útil cuando se ha introducido una expresión y luego se dio cuenta de que hay un error. Se puede recordar la expresión y luego editarla. A diferencia del botón 'ANS', usar 'ENTRADA' dos veces da la entrada antes de la última. Por ejemplo:

Ejemplo$\PageIndex{1}$

Primero preparamos la pantalla:$\boxed{\text{5}}$$\boxed{\text{+}}$$\boxed{\text{5}}$$\boxed{\text{enter}}$$\boxed{\text{2}}$$\boxed{\text{+}}$$\boxed{\text{2}}$$\boxed{\text{enter}}$. Ahora presiona el botón 'ENTRADA'. $2+2$aparece en la ventana. Pulse de nuevo el botón 'ENTRADA'. $5+5$reemplaza el$2+2$.

$clipboard_e46dc781cf8e6cbe48c16c4d9cf7bfd57.png$

Presione$\boxed{\text{enter}}$ (para que 10 sea la respuesta). Para multiplicar el 2+2 por 7 podemos ingresar:$\boxed{\text{2nd}}$$\boxed{\text{enter}}$$\boxed{\text{2nd}}$$\boxed{\text{enter}}$. Después mueve el cursor usando la flecha izquierda hasta la posición de los 2 primeros y presiona$\boxed{\text{2nd}}$$\boxed{\text{del}}$$\boxed{\text{(}}$. Después mueve el cursor usando el botón derecho hasta después del segundo 2 y presiona la secuencia$\boxed{\text{)}}$$\boxed{\times}$$\boxed{\text{7}}$.

$clipboard_e0d359e3fcfe0bae8e73c5108b0bb1f33.png$

¿Qué pasa si dejamos fuera los paréntesis? ¿Podemos entrar$\boxed{\text{(}}$ antes$\boxed{\text{2nd}}$$\boxed{\text{enter}}$?

Ejemplo$\PageIndex{2}$

Primer tipo$\boxed{\text{5}}$$\boxed{\text{+}}$$\boxed{\text{2}}$$\boxed{\text{enter}}$.

Luego escriba$\boxed{\text{2nd}}$$\boxed{\text{(-)}}$$\boxed{\text{+}}$$\boxed{\text{5}}$$\boxed{\text{enter}}$,$\boxed{\text{2nd}}$$\boxed{\text{enter}}$$\boxed{\text{enter}}$,$\boxed{\text{2nd}}$$\boxed{\text{enter}}$$\boxed{\text{enter}}$

$clipboard_e6df73ae745c049b2111d6d7666e909c4.png$

¿Qué hubiera pasado si hubieras usado el botón 'ANS' en lugar del botón 'ENTRADA'?

Ten en cuenta que en lugar del segundo$\boxed{\text{2nd}}$$\boxed{\text{enter}}$$\boxed{\text{enter}}$ podrías haber pulsado$\boxed{\text{enter}}$.

$-$vs$(-)$

Hay dos signos menos en el teclado:$\boxed{\text{-}}$ que está entre$\boxed{\times}$ y$\boxed{\text{+}}$, y$\boxed{\text{(-)}}$ que está a la parte inferior izquierda de$\boxed{\text{enter}}$. ¿Cuál es la diferencia entre los dos? $\boxed{\text{-}}$significa restar. Entonces este es el botón que usas para calcular$7-5$. El botón$\boxed{\text{(-)}}$ significa 'negativo' o 'el opuesto de' así que, por ejemplo, si$-5+7$ quieres computar ingresas$\boxed{\text{(-)}}$$\boxed{\text{5}}$$\boxed{\text{+}}$$\boxed{\text{7}}$. Observe lo que sucede si usa en su lugar$\boxed{\text{-}}$ (¿qué le restará?)! El$\boxed{\text{(-)}}$ botón también es lo que usas para ingresar expresiones como$-x+7$ o$\exp(-x)$.

El botón MODE

Al calcular usando las funciones trigonométricas ($\sin$$\cos$,$\tan$,, y sus inversas) es importante que distingas entre grados y radianes y que estés sincronizado con tu calculadora. Para eso necesitamos mirar la pantalla MODE. Para ver la pantalla Modo pulse$\boxed{\text{mode}}$. La tercera línea tiene las palabras Radián y Grado. Si la palabra 'radián' está resaltada y quieres calcular en grados debes presionar la flecha hacia abajo dos veces (para que la palabra resaltada en la tercera línea parpadee) y luego la flecha derecha y presionar$\boxed{\text{enter}}$. A continuación, debe resaltarse la palabra 'grado'.

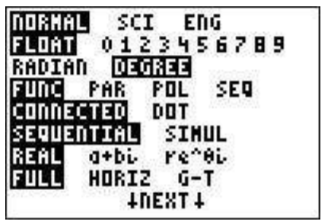
$clipboard_ee781813b3486da57b8bb885ae335e3ac.png$

También puedes verificar tu modo evaluando$\sin (180)$ en la pantalla principal (puedes presionar 'salir' -$\boxed{\text{2nd}}$$\boxed{\text{mode}}$ para volver a la pantalla principal). Si obtienes$0$ como respuesta entonces estás en modo grado. ¿Qué obtienes si estás en modo radián?

El botón STO

Al evaluar expresiones complicadas, a veces es útil usar la función de almacenamiento. Por ejemplo:

Ejemplo$\PageIndex{3}$

Supongamos que quiere evaluar$\dfrac{\left(1-\left(1-\frac 1 2\right)\right)^{2}}{1-\frac 1 2}$. Primero se puede asignar una letra, decir V, el valor$\left(1-\dfrac 1 2\right)$ ya que aparece dos veces. Esto se puede hacer presionando$\boxed{\text{1}}$$\boxed{\text{-}}$$\boxed{\text{1}}$$\boxed{\div}$$\boxed{\text{2}}$$\boxed{\text{sto}}$$\boxed{\text{alpha}}$$\boxed{\text{6}}$. Después evaluar el tipo de expresión original$\boxed{\text{(}}$$\boxed{\text{1}}$$\boxed{\text{-}}$$\boxed{\text{alpha}}$$\boxed{\text{6}}$$\boxed{\text{)}}$$\boxed{x^2}$$\boxed{\div}$$\boxed{\text{alpha}}$$\boxed{\text{6}}$.

$clipboard_e68f2f21c2b61ccaabd3b6a5d229d1005.png$

Tenga en cuenta que puede usar esta función con el botón 'ENTRADA' para evaluar una función en diferentes lugares.

Ejemplo$\PageIndex{4}$

Evaluemos$x^2+x$ en$x=0$ y en$x=1$.
Primer set$x=0$:$\boxed{\text{0}}$$\boxed{\text{sto}}$$\boxed{\text{X,T,}\theta,n}$$\boxed{\text{enter}}$.
Después evalúe la función:$\boxed{\text{X,T,}\theta,n}$$\boxed{x^2}$$\boxed{\text{+}}$$\boxed{\text{X,T,}\theta,n}$$\boxed{\text{enter}}$
Ahora establece$x=1$:$\boxed{\text{1}}$$\boxed{\text{sto}}$$\boxed{\text{X,T,}\theta,n}$
Ahora evalúe nuevamente la función:$\boxed{\text{2nd}}$$\boxed{\text{enter}}$$\boxed{\text{2nd}}$$\boxed{\text{enter}}$$\boxed{\text{enter}}$.

Tenga en cuenta que hay otra manera de evaluar una función en varios puntos que se introducirá a continuación en la sección de gráficos.

Search

Ejemplo\(\PageIndex{1}\)

Ejemplo\(\PageIndex{2}\)

\(-\)vs\((-)\)

El botón MODE

El botón STO

Ejemplo\(\PageIndex{3}\)

Ejemplo\(\PageIndex{4}\)