26.4: A.4- Graficar una función definida por partes

Última actualización
Guardar como PDF

Page ID: 117813

Thomas Tradler and Holly Carley
CUNY New York City College of Technology via New York City College of Technology at CUNY Academic Works

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Supongamos que desea graficar la función definida por partes

\[f(x)= \begin{cases}x^{2}, & x<2 \\ 2 x-7, & x \geq 2\end{cases} \nonumber \]

Ir al menú. Necesitamos ingresar a la función de la siguiente manera:

\[y=x^2(x<2)+(2x-7)(x\geq 2) \nonumber \]

Las únicas entradas nuevas están en los signos de desigualdad, a los que se puede acceder a través del menú “TEST” ($\boxed{\text{2nd}}$$\boxed{\text{math}}$).

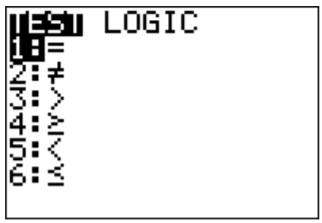
$clipboard_e00458173c770b3ce1d25c933f8a92b83.png$

Por lo tanto, presionamos las teclas:$\boxed{\text{X,T,}\theta,n}$$\boxed{x^2}$$\boxed{\text{(}}$$\boxed{\text{X,T,}\theta,n}$$\boxed{\text{2nd}}$$\boxed{\text{math}}$$\boxed{\text{5}}$$\boxed{\text{2}}$$\boxed{\text{)}}$$\boxed{\text{+}}$$\boxed{\text{(}}$$\boxed{\text{2}}$$\boxed{\text{X,T,}\theta,n}$$\boxed{\text{-}}$$\boxed{\text{7}}$$\boxed{\text{)}}$$\boxed{\text{(}}$$\boxed{\text{X,T,}\theta,n}$$\boxed{\text{2nd}}$$\boxed{\text{math}}$$\boxed{\text{4}}$$\boxed{\text{2}}$$\boxed{\text{)}}$$\boxed{\text{enter}}$. El gráfico se muestra a la derecha:

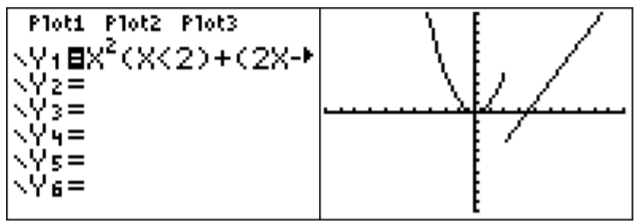
$clipboard_ecdb4a1e4a5c2fcdbbd440e748f853fdc.png$

El significado de$y=(x<2)$ como función es que es igual a$1$ cuando es verdad y$0$ cuando es falso. En otras palabras, la expresión$(x<2)$ es$1$ cuándo$x<2$ y de$0$ otra manera. Puedes usar esta idea para graficar funciones más complicadas. Por ejemplo para ingresar$x+2$ para$0<x<3$ usted podría ingresar$(x+2)(0<x)(x<3)$.

Nota: Al graficar funciones definidas por partes, la gráfica a veces es diferente de lo que se espera. Consulte la sección de errores comunes para interpretar la gráfica resultante a continuación.

Graficar con coordenadas polares

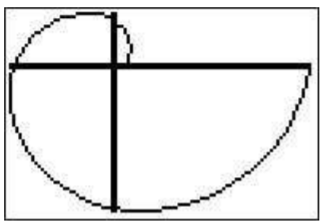
Supongamos que quiere graficar la curva$r=\theta+\sin\theta$. Prensa$\boxed{\text{mode}}$. En la cuarta línea resalte 'Pol' y presiona$\boxed{\text{enter}}$ (asegúrate de que también en modo radián)

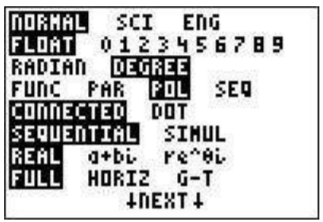
$clipboard_eb6f5b42496732d9ff319110b51c706b2.png$

y prensa$\boxed{y=}$. Tu menú tendrá una lista$r_1, r_2,...$. Después del$r_1$ tipo$\boxed{\text{X,T,}\theta,n}$$\boxed{\text{+}}$$\boxed{\sin}$$\boxed{\text{X,T,}\theta,n}$$\boxed{\text{)}}$. Después para ver el tipo de gráfico$\boxed{\text{graph}}$. Es posible que tenga que ajustar su ventana (ajuste de zoom) para ver la espiral resultante.

$clipboard_e627ad93867bd053e1e42021e6f9ed5a7.png$

Graficar con coordenadas paramétricas

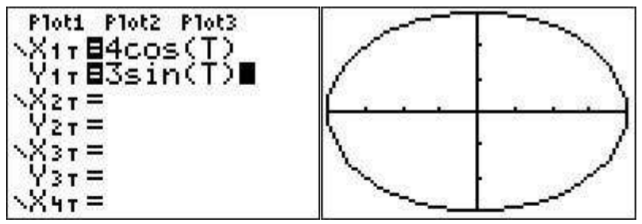
Supongamos que desea graficar la curva dada por$y(t)=3\sin(t), x(t)=4\cos(t)$. Primero tenemos que ajustar el modo a modo paramétrico: presione$\boxed{\text{mode}}$ y resalte 'PAR' en la cuarta línea y presione$\boxed{\text{enter}}$.

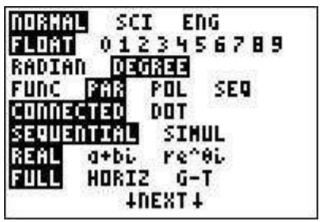
$clipboard_eef3892a9905431d18364c130a7a7af89.png$

Ahora ve a la pantalla gráfica. Verás una lista que comienza con X$_{1T}$ e Y$_{1T}$. A la derecha del$_{1T}$ tipo X$\boxed{\text{4}}$$\boxed{\cos}$$\boxed{\text{X,T,}\theta,n}$ y a la derecha del$_{1T}$ tipo$\boxed{\text{3}}$$\boxed{\sin}$$\boxed{\text{X,T,}\theta,n}$ Y. Después para ver la gráfica presione$\boxed{\text{graph}}$. Es posible que necesite$\boxed{\text{zoom}}$$\boxed{\text{0}}$ (zoomfit) para ver la elipse resultante. (Además, tenga en cuenta que la escala puede ser engañosa, es posible que desee$\boxed{\text{zoom}}$$\boxed{\text{5}}$ para una comprensión más clara de la gráfica).

$clipboard_e7936156a4fcf3180efef0b83a3b0badc.png$