2.2: Resolver desigualdades

Última actualización
Guardar como PDF

Page ID: 114028

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En esta sección, veremos la solución de las desigualdades. A menudo trabajarás con desigualdades en el cálculo, particularmente cuando trabajas con derivados. Una derivada es una función que le indica la rapidez con la que cambia una función relacionada. Una derivada positiva te dice que la función está aumentando y una derivada negativa te dice que la función está disminuyendo. Esto significa que necesitarás poder identificar cuándo la derivada es mayor que cero y cuándo es menor que cero.

Al resolver desigualdades, los matemáticos expresan sus respuestas utilizando la notación de intervalos, una forma especial de expresar un intervalo de números. Los intervalos nos dirán cuando la desigualdad es una afirmación verdadera, es decir, nos dicen todos los valores de entrada que hacen válida la desigualdad. También escuchará a los matemáticos usar la frase “la desigualdad sostiene para... '; esta es otra manera de decir que estos son los insumos que hacen realidad la desigualdad. Familiaricémonos con la notación de intervalos antes de mirar las desigualdades.

2.2.1 Notación de intervalos

Antes de llegar a resolver las desigualdades, discutiremos la notación de intervalos. La notación de intervalos nos proporciona una manera de describir los rangos de números de manera concisa. A diferencia del orden de las operaciones, con notación de intervalo, los paréntesis y los corchetes tienen Por ejemplo,$[1,4.5]$ es el rango de números entre 1 y 4.5, incluyendo esos puntos finales. Por ejemplo, 1, 2$\pi$, y 4.5 están todos incluidos en ese intervalo, pero -1.2, 85 y 4.5000001 no lo están. No obstante, si nos fijamos en$(1,4.5)$, 2 y$\pi$ siguen en este intervalo pero 1 y 4.5 no lo están. Los corchetes nos dicen que incluimos el punto final y los paréntesis nos dicen que no lo hacemos.

Con la notación de intervalos, podemos mezclar paréntesis y corchetes si necesitamos incluir un punto final pero no el otro. Por ejemplo,$[1,4.5)$ contiene 1 pero no 4.5 y$(1,4.5]$ contiene 4.5 pero no 1.

Ejemplo$\PageIndex{1}$: Interval Notation

Determinar si cada uno de los siguientes números está incluido en el intervalo$[-5, 27)$.

\[\begin{array}{lll}{\text{1. }2}&{\qquad}&{\text{5. }27} \\ {\text{2. }\pi}&{\qquad}&{\text{6. }32} \\ {\text{3. }-5}&{\qquad}&{\text{7. }-5.000001} \\ {\text{4. }-8}&{\qquad}&{\text{8. }-4.999999}\end{array}\nonumber\]

Solución

Para cada uno de estos, necesitamos determinar si el número está entre los dos números dados en el intervalo.

$2$es mayor$-5$ y menor que$27$ así que está en el intervalo.
$\pi$es mayor$-5$ y menor que$27$ así que está en el intervalo.
$-5$es uno de nuestros puntos finales, por lo que necesitamos ver si tiene un paréntesis o un paréntesis en ese extremo. Tiene un soporte, por lo que se incluye en el intervalo.
$-8$es menor que$-5$, por lo que no se incluye en el intervalo.
$27$es uno de nuestros puntos finales, por lo que necesitamos ver si tiene un paréntesis o un paréntesis en ese extremo. Tiene paréntesis, por lo que no se incluye en el intervalo.
$32$es mayor que$27$, por lo que no está incluido en el intervalo.
$-5.000001$es menor que$-5$, por lo que no se incluye en el intervalo.
$-4.999999$es mayor$-5$ y menor que$27$ así que está en el intervalo.

\[2,\: \pi,\: -5,\text{ and }-4.999999\text{ are in the interval}\]

\[-8,\: 27,\: 32,\text{ and }-5.000001\text{ are not in the interval}\]

También podemos usar la notación de intervalos para expresar rangos que no tienen un límite superior. Por ejemplo, si quisiéramos usar notación de intervalo para escribir el rango para todos los números positivos, escribiríamos$(0,\infty)$. Sabemos que no hay límite para qué tan grande puede llegar a ser un número positivo, así que usamos$\infty$ para indicar que solo estamos mirando números mayores que$0$. Del mismo modo, podemos escribir$(-\infty,0)$ para expresar el rango para todos los números negativos. Tenga en cuenta que para ambos usamos un paréntesis con el símbolo del infinito y no un corchete ya que el infinito no es un número.

Adicionalmente, podemos usar la notación de intervalos para expresar rangos de números más complicados. Podemos combinar rangos usando$\cup$, la forma matemática taquigráfica de escribir “o”. Por ejemplo,$[1,3]\cup(4,\infty)$ significa el rango de valores entre 1 y 3, incluyendo los puntos finales, así como cualquier número mayor que 4. Entonces 2, 4.1 y 20 están todos en este intervalo, pero -2, 3.5, y 4 no lo están. También podemos usar la notación para limitar rangos usando$\cap$, la forma matemática taquigráfica de escribir “y también”. Por ejemplo, si tenemos dos rangos, digamos$(1,4]$ y$[2,8)$, y sólo nos interesan los números que están en ambos rangos, podemos escribir$(1,4] \cap [2,8)$. Podemos usar este símbolo para ayudar a mostrar nuestro trabajo, pero para nuestra respuesta final siempre debemos simplificar para que no necesitemos usar el$\cap$ símbolo (está bien, y bastante común, usar el$\cup$ símbolo como parte de tu respuesta final). Dijimos eso$\cap$ significa que solo queremos los números que están en ambos intervalos; el número más pequeño contenido por ambos intervalos es 2 y el más grande es 4, así que podemos escribir$(1,4] \cap [2,8) = [2,4]$ en su lugar.

2.2.2 Notación de intervalos y desigualdades

La notación de intervalos también nos da otra forma de expresar una desigualdad. Por ejemplo, se$x\geq 2$ puede escribir como$x \in [2,\infty)$. Aquí el$\in$ símbolo se lee como la palabra “en”. Leeríamos esto en voz alta diciendo que “x es mayor o igual a 2” es lo mismo que “x está en el rango de 2, inclusive, hasta el infinito”. El enunciado$x \in (2,\infty)$ es un poco diferente; es lo mismo$x > 2$ que ya que no queremos incluir 2 como parte de nuestra gama. Aquí, leeríamos el rango como “x en 2, exclusivo, hasta el infinito”. Los símbolos que aprendimos antes,$\cup$ y$\cap$ se leen como “unión” y “se cruzan”, respectivamente.

Al trabajar con las desigualdades, iniciaremos todos los problemas de desigualdad convirtiéndolos en problemas de igualdad. Esto nos permitirá utilizar algunas técnicas que ya hemos visto cuando discutimos factorización y raíces de una función. La (s) solución (es) al problema de igualdad nos dirá los “puntos de ruptura”, los valores de entrada donde la desigualdad puede pasar de ser verdadera a ser falsa. Vamos a probar valores en ambos lados de cada punto de ruptura para ver dónde es verdadera la desigualdad. Trabajaremos cuidadosamente para asegurarnos de que encontremos todos los puntos de ruptura porque no queremos perdernos ningún lugar donde la desigualdad pueda cambiar de verdadera a falsa. Veamos algunos ejemplos sencillos antes de pasar a las desigualdades más complicadas.

Ejemplo$\PageIndex{2}$: Polynomial Inequality

Resolver$x^2 -6x +8 >0$.

Solución

Nuestro primer paso es convertir esto en una declaración de igualdad cambiando el$>$ símbolo a un$=$ símbolo:\[x^2-6x+8 =0\] Ahora, podemos usar cualquier método de solución que aprendimos para encontrar las raíces de una función cuadrática para resolver. Aquí tenemos una cuadrática que facciona muy bien, así que tomaremos ese enfoque, pero podrías usar la fórmula cuadrática si lo prefieres. \[\begin{align}\begin{aligned}\begin{split} x^2 -6x+8 & = 0 \\ (x-2)(x-4) & = 0 \\ x & =2,4 \end{split}\end{aligned}\end{align}\]Esto nos dice que los puntos de quiebre son$x=2$ y$x=4$. Estos son los únicos lugares en los que la desigualdad podría cambiar de ser verdadera a ser falsa para este tipo de funciones. Vamos a probar valores en cada lado de ambos puntos de ruptura; esto significa que necesitamos probar un valor que sea menor que 2, un valor entre 2 y 4, y un valor mayor que 4. Nos gusta trabajar de izquierda a derecha, por lo que comenzaremos probando un valor menor a 2. Podemos escoger cualquier número que sea menor a 2, pero usaremos 0 porque es fácil trabajar con él. Si sustituimos en$x=0$ obtenemos:\[x^2-6x + 8 = (0)^2-6(0)+8 = 8 >0\] Obtenemos 8, que es mayor que 0, por lo que la desigualdad es cierta para todos los valores menores que 2. A continuación, necesitamos probar un valor entre 2 y 4; 3 parece la opción más fácil. \[x^2-6x + 8 = (3)^2-6(3)+8 = 9-18+8 = -1 <0\]Obtenemos un número negativo, por lo que la desigualdad es falsa para todo entre 2 y 4. Ahora, necesitamos probar algo más grande que 4. Usaremos 5, pero puedes elegir cualquier número, siempre y cuando sea mayor que 4. \[x^2-6x + 8 = (5)^2-6(5)+8 = 25 - 30 + 8 = 3 >0\]El resultado es positivo, por lo que la desigualdad es cierta. Ahora, tenemos que la desigualdad es cierta para números menores que 2 y números mayores que 4. No es cierto para$x=2$ o$x=4$ ya que ambos hacen que el lado izquierdo 0 y queremos que el lado izquierdo sea mayor que 0, no igual a él. En notación de intervalos, tenemos:

\[x\in (-\infty,2)\cup(4,\infty)\]

En este ejemplo, tenemos una estricta desigualdad. Nosotros decimos que es estricto porque lo es$>$ y no$\geq$. De igual manera, diríamos que una desigualdad con$<$ es estricta. Con desigualdades estrictas, nuestra respuesta final no incluirá los puntos de ruptura, por lo que usaremos paréntesis en estos puntos de ruptura porque no queremos incluir estos puntos.

Muchas personas usarán una línea numérica cuando se trabaja con desigualdades. Al usar una línea numérica, marcaría cada punto de ruptura, y luego sombrearía o marcaría de otra manera los intervalos donde la desigualdad es verdadera. Para el problema anterior, esto se vería así:

$clipboard_e887da776a4c27b2501d502a3cefd983f.png$

Figura$\PageIndex{1}$

Dado que tenemos una desigualdad estricta (es decir, tenemos$>$ o$<$ así que somos estrictamente mayores o estrictamente menores que), utilizamos círculos abiertos para marcar nuestros puntos de quiebre. Esto nos recuerda que no incluimos estos puntos en nuestros intervalos. Algunas personas usarán marcas de verificación y X en su lugar, con una marca de verificación que indica dónde se mantiene la desigualdad y una X donde no. Esto se vería así:

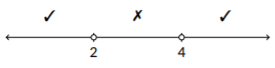
$clipboard_edde570b2cca207199153c2ce4b47ac88.png$

Figura$\PageIndex{2}$

Estas líneas numéricos se vuelven bastante útiles si tienes muchos puntos de quiebre. Lo dejan muy claro para que puedas estar seguro de probar un punto en cada intervalo. También podemos usar una tabla para resumir los resultados, en lugar de usar una línea numérica. La tabla tiene algunas ventajas clave: resume claramente tu trabajo haciendo que tu proceso de pensamiento sea más fácil de seguir y ayudará a eliminar errores descuidados de tu trabajo. Una tabla para el ejemplo anterior podría verse así:

	$(-\infty,2)$	$(2,4)$	$(4,\infty)$
Valor a verificar:	\ ((-\ infty,2)\) ">0	\ ((2,4)\) ">3	\ ((4,\ infty)\) ">5
Resultado:	\ ((-\ infty,2)\) ">$8>0$	\ ((2,4)\) ">$-1>0$	\ ((4,\ infty)\) ">$3>0$
T/F:	\ ((-\ infty,2)\) ">Verdadero	\ ((2,4)\) ">Falso	\ ((4,\ infty)\) ">Verdadero

Mesa$\PageIndex{1}$

Cualquiera de estos métodos son apropiados para mostrar claramente su trabajo; el que elija es una cuestión de preferencia personal.

2.2.3: Incorporación de puntos indefinidos

Señalamos anteriormente que nuestra desigualdad puede cambiar de verdadera a falsa en nuestros puntos de quiebre, los puntos donde la declaración de igualdad es cierta. La desigualdad también puede cambiar de verdadera a falsa en lugares donde la función es indefinida. Por ejemplo, sabemos que la función$f(x) = \frac{1}{x}$ es positiva cuando$x$ es positiva y negativa cuando$x$ es negativa. Esto quiere decir que la desigualdad se$\frac{1}{x}>0$ mantiene, o es cierta, sólo para$x \in (0,\infty)$. No obstante, no hay lugares donde$f(x)=0$. Dado que no$f(x)$ está definido en$x=0$, introduce un tipo diferente de punto de ruptura; uno donde la gráfica de la función se “rompe” porque no se puede graficar donde está indefinida. Echemos un vistazo a un ejemplo donde tenemos que incorporar puntos indefinidos al incluir puntos de ruptura adicionales.

Ejemplo$\PageIndex{3}$: Solving a Rational Inequality

Resolver$\displaystyle \frac{x-5}{x^2-4} \geq 0$.

Solución

Empezaremos convirtiendo la desigualdad en una declaración de igualdad y resolviendo para$x$. Para ayudar a resolver para$x$, nos desharemos de la fracción multiplicando ambos lados por el denominador completo; esto nos permitirá cancelar el denominador del lado izquierdo. \[\begin{align}\begin{aligned}\begin{split} \frac{x-5}{x^2-4} &= 0 \\ (x^2-4) \Bigg(\frac{x-5}{x^2-4} \Bigg) & = (x^2-4)(0) \\ x-5 &= 0 \\ x &= 5 \end{split}\end{aligned}\end{align}\]Esto nos da un punto de quiebre en$x=5$. A continuación, necesitaremos ver si la función está indefinida en algún punto. Al ser una función racional (una fracción con un polinomio en el numerador y un polinomio en el denominador), sabemos que no está definida en cualquier lugar que el denominador sea igual a cero. Busquemos estos puntos:\[\begin{align}\begin{aligned}\begin{split} x^2 - 4 &= 0 \\ (x-2)(x+2) & = 0 \\ x &= 2, -2 \end{split}\end{aligned}\end{align}\] Vemos que no$\frac{x-5}{x^2-4}$ está definido para$x=2$ y$x=-2$. Esto nos da dos puntos de quiebre adicionales. Eso significa que tenemos tres puntos de quiebre:$x=5$,$x=2$, y$x=-2$. Marquemos estos en una línea numérica. Dado que esto no es una desigualdad estricta, usaremos círculos cerrados para marcar el punto de quiebre en$x=5$. Sin embargo, todavía necesitamos usar círculos abiertos en$x=2$ y$x=-2$ porque la función no está definida en estos puntos y no los incluiremos en nuestros intervalos.

$clipboard_e569a79e4a6069822c52d0d66c0478f2b.png$

Figura$\PageIndex{3}$

Ahora, necesitamos verificar valores en cada intervalo. Primero, verificaremos algo menos que$-2$; usaremos$x=-3$. Sustituyendo, da$\frac{(-3)-5}{(-3)^2 -4} = \frac{-8}{5}$. Esto es menor que 0; esto significa que podemos colocar una marca x sobre este intervalo:

$clipboard_e5656c1c13d9e31ce7fd058a9a34f5d6d.png$

Figura$\PageIndex{4}$

Ahora, para comprobar algo entre$-2$ y$2$. Vamos a usar$x=0$. Sustituyendo da$\frac{(0)-5}{(0)^2-4} = \frac{-5}{-4} =\frac{5}{4} >0$. Esto significa que podemos colocar una marca de verificación en este intervalo:

$clipboard_eaae4747c1ba8ce2024cb86d90d7dc2fa.png$

Figura$\PageIndex{5}$

Now, we need to check a value between $2$ and $5$. We’ll use $x=3$. We get $\frac{(3)-5}{(3)^2-4}=\frac{-2}{5} <0$, so this interval gets an x-mark.

$clipboard_eee01d0fd563f1a34b8459584c898f763.png$

Figura$\PageIndex{6}$

Por último, necesitamos verificar un valor mayor que$5$. Vamos a usar$x=6$. Esto da$\frac{(6)-5}{(6)^2-4} = \frac{1}{32} >0$, por lo que este intervalo obtiene una marca de verificación.

$clipboard_e65c2b2f100340a0bda24e8907c070ea2.png$

Figura$\PageIndex{7}$

Ahora tenemos una marca en cada intervalo, así podemos determinar nuestra respuesta final. Podemos ver que la desigualdad es cierta para$x \in (-2,2) \cup [5,\infty)$. Tenga en cuenta que incluimos$x=5$ ya que tiene un círculo cerrado y excluido$x=-2$ y$x=2$ ya que tienen círculos abiertos. Nuestra respuesta final es

\[\frac{x-5}{x^{2}-4}\geq 0\text{ holds for }x\in (-2,2)\cup [5,\:\infty )\]