4.7: Inflación y tasas de interés

Última actualización
Guardar como PDF

Page ID: 58974

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

¿Cuál es la diferencia entre las tasas de interés reales y nominales y por qué es importante la distinción?

Bien podría preguntarse en este punto, ¿Qué factores cambian las tasas de interés? Un factor importante es la inflación. A medida que sube el nivel de precios, también lo hacen las tasas de interés, o al menos lo que los economistas llaman tasas de interés nominales, el tipo de tasas que hemos discutido hasta ahora. Si las tasas nominales no aumentan (y a menudo no lo hacen, o no pueden), los prestamistas podrían recibir más dólares nominales de los que prestaron pero en realidad recuperar menos poder adquisitivo. Imagina, por ejemplo, que prestaste 100 dólares por un año al 6 por ciento de interés cuando una barra de pan, un paquete de chicle y una botella de dos litros de Mountain Dew cuestan cada uno $1. Al finalizar el préstamo simple, recuperarías $100 × 1.06 = $106 y podrías disfrutar de un extra de $6 de bienes, digamos, dos hogazas de pan, dos paquetes de chicle, y dos botellas de la fiebre de cafeína y azúcar conocida como Doin' the Dew. Pero, ¿y si los precios se duplicaron durante ese año En lugar de alguna combinación de 106 golosinas, solo podrías comprar cincuenta y tres. Tu rendimiento nominal sería positivo, pero tu rendimiento real, lo que realmente podrías comprar con los $106, sería abruptamente negativo.

Una ecuación simple, la ecuación de Fisher, que lleva el nombre de Irving Fisher, el economista estadounidense de principios del siglo XX que la articuló, ^[1] nos ayuda a comprender con mayor precisión la relación entre la inflación y las tasas de interés:

\ [i = i_r + π\\
\ textrm {o, reordenando los términos,}\\
i_r = i - π\\
\ textrm {o, nuevamente reordenando los términos,}\\
π = i - i_r\ nonumber\]

donde

i _r = la tasa de interés real

i = la tasa de interés nominal (el tipo de tasa de interés la primera parte de este capítulo discutida exclusivamente)

$\pi$= inflación (o inflación esperada)

En inglés sencillo, después del hecho (ex post en la lengua de los economistas), la tasa de interés nominal es igual a la tasa de interés real más la inflación real. Antes del hecho (ex ante en la lengua de los economistas), la tasa de interés nominal es igual a la tasa de interés real más la expectativa de inflación.

Stop and Think Box

A principios de 2007, a un hombre le devolvieron una billetera que había perdido más de sesenta años antes en Francia, durante la Segunda Guerra Mundial. ^[2] Además de su tarjeta original del Seguro Social y una foto de sus padres, el hombre recibió una suma no especificada de efectivo. ¿Perder la billetera fue una buena inversión? ¿Por qué o por qué no?

No, porque el riesgo de que nunca fuera devuelto era muy alto. Además, el dólar perdió una cantidad significativa de su poder adquisitivo durante el periodo debido a la inflación y el dinero no ganó intereses. Con tan solo 3 por ciento compuesto anualmente, $100 habrían crecido a 100 × (1.03) ⁶⁰ = $589.16 después de 60 años. Al 6 por ciento, $100 habrían crecido a 100 × (1.06) ⁶⁰ = $3,298.77.

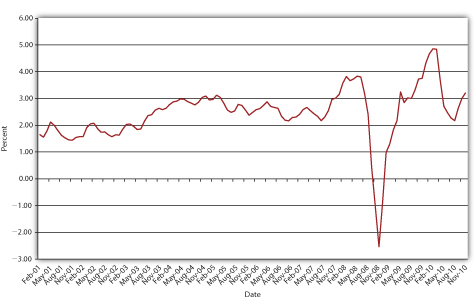
Tradicionalmente, las expectativas de inflación eran inobservables por lo que las tasas reales solo se conocían ex post. Sin embargo, tipos relativamente nuevos y especiales de bonos indexados a la inflación, llamados Valores de Protección contra la Inflación del Tesoro (TIPS), proporcionan información real sobre las tasas de interés, permitiendo a los participantes del mercado observar las expectativas de inflación ex Por ejemplo, si el rendimiento a vencimiento de un bono del Tesoro regular no indexado a diez años es de 5 por ciento, y el rendimiento en los TIPS a diez años es de 2 por ciento, la expectativa de inflación, a través de la Ecuación de Fisher π = i − i _r, es 5 −2 = 3 por ciento. La Figura 4.5 “Tasa de interés real estadounidense, 2001-2010" muestra cómo las expectativas de inflación han aumentado y disminuido desde la introducción del TIPS en 1997.

CLAVE PARA TOMAR

La diferencia entre la tasa de interés real y la nominal es literalmente inflación o expectativas de inflación.
De acuerdo con la Ecuación de Fisher, el interés nominal es igual al interés real más la inflación (o expectativas de inflación), o el interés real es igual al interés nominal menos la inflación (expectativas).
Si la inflación real supera las expectativas de inflación, los rendimientos reales ex post (ajustados por inflación, después del hecho) de los bonos pueden ser negativos.

[1] Para ser francos, Benjamin Franklin y otros colonos de la América del siglo XVIII lo entendieron bien.

[2] Video de ABC News, “Cartera devuelta, 60 años después, Un veterano de la Segunda Guerra Mundial le devuelve la billetera sesenta años después” (1/9/2007).