21.2: El modelo IS-LM

objetivos de aprendizaje

1. ¿Cuáles son las curvas IS y LM?
2. ¿Cuáles son sus características?
3. ¿Qué aprendemos cuando combinamos las curvas IS y LM en una gráfica?
4. ¿Por qué se logra el equilibrio?
5. ¿Cuál es el mayor inconveniente del modelo IS-LM?

El marco keynesiano del diagrama cruzado es genial, hasta donde va. Tenga en cuenta que no tiene nada que decir sobre las tasas de interés o el dinero, ¡una carencia importante para nosotros los estudiantes del dinero, la banca y la política monetaria! Sin embargo, nos ayuda a construir un modelo más potente que examine el equilibrio en los mercados de bienes y dinero, las curvas IS (inversión-ahorro) y LM (preferencia de liquidad—dinero), respectivamente (de ahí el nombre del modelo).

Las tasas de interés están negativamente relacionadas con I y con NX. El razonamiento aquí es sencillo. Cuando las tasas de interés (i) son altas, las empresas prefieren invertir en bonos que en planta física (porque menos proyectos son valor presente neto positivo o +VAN) o inventario (porque tiene un alto costo de oportunidad), por lo que I (inversión) es baja. Cuando las tarifas son bajas, la nueva planta física y los inventarios se ven baratos y muchos más proyectos son +VPN (i ha bajado en el denominador de la fórmula de valor presente), por lo que es alto. De igual manera, cuando i es baja la moneda nacional será débil, todo lo demás igual. Se facilitarán las exportaciones y las importaciones disminuirán porque los bienes extranjeros se verán caros. Así, NX será alto (exportaciones > importaciones). Cuando i es alto, por el contrario, la moneda nacional estará en demanda y por lo tanto fuerte. Eso perjudicará las exportaciones e incrementará las importaciones, por lo que NX caerá y tal vez se volverá negativo (exportaciones < importaciones).

Ahora piensa en el _anuncio Y en un diagrama transversal keynesiano. Como vimos anteriormente, la producción agregada aumentará como lo hagan I y NX. Entonces sabemos que a medida que yo aumenta, Y _ad disminuye, ceteris paribus. Trazar la tasa de interés en el eje vertical contra la salida agregada en el eje horizontal, como se muestra a continuación, nos da una curva inclinada hacia abajo. ¡Esa es la curva IS! Por cada tasa de interés, nos dice en qué momento el mercado de bienes (I y NX, ¿lo entiendes?) está en equilibrio, manteniendo constantes el consumo autónomo, la política fiscal y otros determinantes de la demanda agregada. Para todos los puntos a la derecha de la curva, existe un exceso de oferta de bienes para esa tasa de interés, lo que provoca que las empresas disminuyan los inventarios, lo que lleva a una caída en la producción hacia la curva. Para todos los puntos a la izquierda de la curva IS, persiste un exceso de demanda de bienes, lo que induce a las empresas a aumentar los inventarios, lo que lleva a un aumento de la producción hacia la curva.

Obviamente, la curva IS por sí sola es tan insuficiente para determinar i o Y como la demanda por sí sola lo es para determinar precios o cantidades en el modelo estándar de precios microeconómicos de oferta y demanda. Necesitamos otra curva, una que se incine hacia el otro lado, es decir, hacia arriba. Esa curva se llama la curva LM y representa puntos de equilibrio en el mercado para el dinero. La demanda de dinero está relacionada positivamente con los ingresos porque más ingresos significa más transacciones y porque más ingresos significa más activos, y el dinero es uno de esos activos. De manera que podemos trazar de inmediato una curva LM con pendiente ascendente, una curva que mantiene constante la oferta monetaria. A la izquierda de la curva LM hay un exceso de oferta de dinero dada la tasa de interés y la cantidad de salida. Eso hará que la gente use su dinero para comprar bonos, impulsando así los precios de los bonos al alza y, por lo tanto, yo bajé a la curva LM. A la derecha de la curva LM, hay un exceso de demanda de dinero, induciendo a la gente a vender bonos por dinero en efectivo, lo que hace que los precios de los bonos bajen y por lo tanto yo suban a la curva LM.

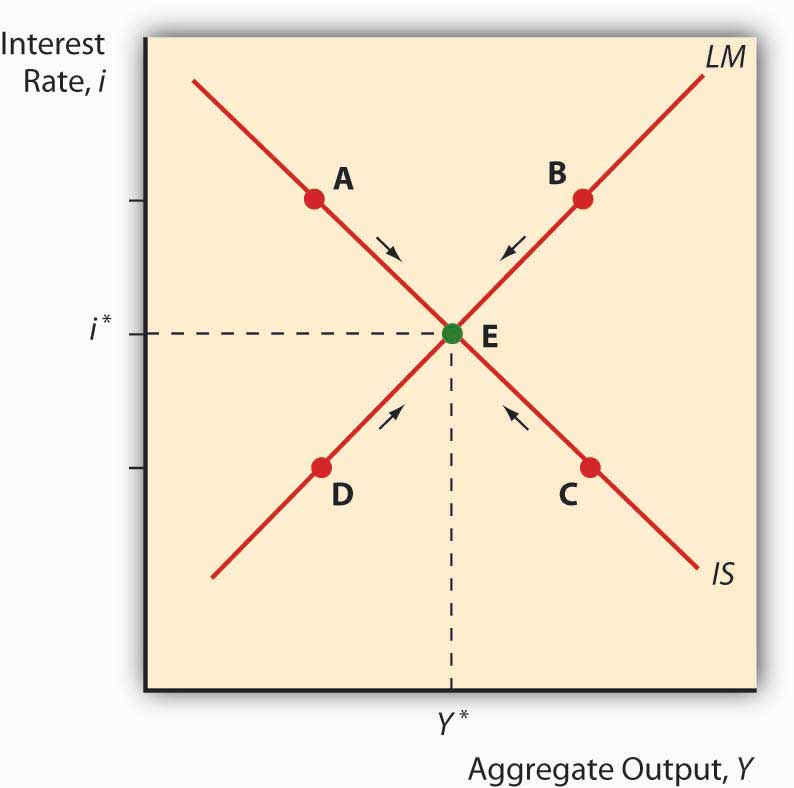
Cuando colocamos las curvas IS y LM en la gráfica al mismo tiempo, como en la Figura 21.4 “Diagrama IS-LM: equilibrio en los mercados de dinero y bienes”, inmediatamente vemos que solo hay un punto, su intersección, donde los mercados tanto de bienes como de dinero están en equilibrio. Tanto la tasa de interés como la producción agregada están determinados por esa intersección. Luego podemos cambiar las curvas IS y LM para ver cómo afectan las tasas de interés y la producción, i* e Y*. En el siguiente capítulo, veremos cómo los formuladores de políticas manipulan esas curvas para aumentar la producción. Pero todavía no vamos a terminar porque, como se mencionó anteriormente, el modelo IS-LM tiene un inconveniente importante: funciona sólo a corto plazo o cuando el nivel de precios es fijo de otra manera.

Figura\(\PageIndex{4}\): Diagrama IS-LM: equilibrio en los mercados de dinero y bienes

Stop and Think Box

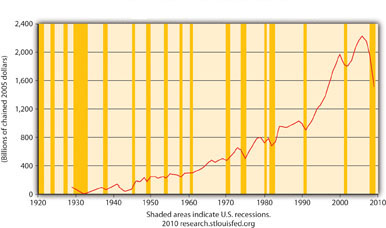
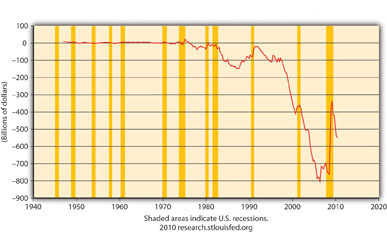
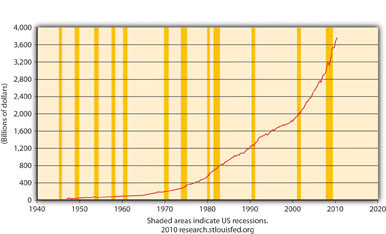
¿Tiene sentido la Figura 21.5? ¿Por qué o por qué no? ¿Qué significa la Figura 21.6? ¿Por qué la Figura 21.7 no es una buena representación de G?

Figura\(\PageIndex{5}\): Inversión Interior Privada Bruta Real (GIDICA), 1925—2010

Fuente: Departamento de Comercio de Estados Unidos, Bureua de Análisis Económico

Figura\(\PageIndex{6}\): Exportación Neta de Bienes y Servicios (NETEXP), 1945—2010

Fuente: Departamento de Comercio de Estados Unidos, Bureua de Análisis Económico

Figura\(\PageIndex{7}\): Gastos corrientes del Gobierno Federal (FGEXPND), 1945—2010

Fuente: Departamento de Comercio de Estados Unidos, Bureua de Análisis Económico

La figura 21.5 tiene perfectamente sentido porque representa I en la ecuación Y = Y _ad = C + I + G + NX, y las áreas sombreadas representan recesiones, es decir, disminuciones en Y. Obsérvese que antes de casi todas las recesiones del siglo XX, bajé.

La figura 21.6 significa que NX en Estados Unidos es considerablemente negativo, que las exportaciones < importaciones por un amplio margen, creando un drenaje significativo sobre Y (PIB). Tenga en cuenta que NX mejoró (se volvió menos negativo) durante la crisis y la recesión resultante pero volvió a caer durante la recuperación de 2010.

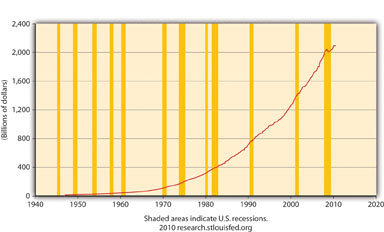
La Figura 21.7 no es una buena representación de G porque ignora los gastos de los gobiernos estatales y locales, que son significativos en Estados Unidos, como muestra la Figura 21.8.

Figura\(\PageIndex{8}\): Gastos corrientes de Estados y gobiernos locales (SLEXPND), 1945—2010

Fuente: Departamento de Comercio de Estados Unidos, Bureua de Análisis Económico

claves para llevar

• La curva IS muestra los puntos en los que la cantidad de bienes suministrados es igual a la demandada.
• En una gráfica con interés (i) en el eje vertical y salida agregada (Y) en el eje horizontal, la curva IS se inclinó hacia abajo porque, a medida que aumenta la tasa de interés, los componentes clave de Y, I y NX, disminuyen. Esto se debe a que a medida que aumenta i, el costo de oportunidad de mantener el inventario aumenta, por lo que los niveles de inventario disminuyen y los proyectos de +VPN que involucran nueva planta física se vuelven más raros, y yo disminuye.
• Además, alto i significa una moneda nacional fuerte, todo lo demás constante, lo cual es una mala noticia para las exportaciones y una buena noticia para las importaciones, lo que significa que NX también cae.
• La curva LM traza los puntos de equilibrio para diferentes tipos de interés donde la cantidad de dinero demandada es igual a la cantidad de dinero suministrado.
• Inclina hacia arriba porque a medida que Y aumenta, la gente quiere retener más dinero, impulsando así i hacia arriba.
• La intersección de las curvas IS y LM indica la tasa de interés de equilibrio de la macroeconomía (i*) y la producción (Y*), punto donde el mercado de bienes y el mercado de dinero están ambos en equilibrio.
• En todos los puntos a la izquierda de la curva LM, existe un exceso de oferta de dinero, induciendo a la gente a renunciar al dinero por bonos (para comprar bonos), impulsando así el alza de los precios de los bonos y las tasas de interés a la baja hacia el equilibrio.
• En todos los puntos a la derecha de la curva LM, existe un exceso de demanda de dinero, induciendo a la gente a renunciar a los bonos por dinero (para vender bonos), lo que impulsa a la baja los precios de los bonos y a las tasas de interés hacia el equilibrio.
• En todos los puntos a la izquierda de la curva IS, existe un exceso de demanda de bienes, provocando que los niveles de inventario caigan e induciendo a las empresas a incrementar la producción, lo que lleva a un incremento en la producción.
• En todos los puntos a la derecha de la curva IS, existe un exceso de oferta de bienes, creando un exceso de inventario que induce a las empresas a recortar la producción, disminuyendo así Y hacia el equilibrio.
• El mayor inconveniente del modelo IS-LM es que no considera cambios en el nivel de precios, por lo que en la mayoría de las situaciones modernas, solo es aplicable a corto plazo.