4.3: Modelos de Regresión
- Page ID
- 59656
Un enfoque más complicado de modelización de deterioro que los de la sección anterior emplea enfoques estadísticos, más comúnmente análisis de regresión. Estos modelos se basan en observaciones de historia y condiciones pasadas. Los modelos pueden indicar la correlación entre condiciones y factores explicativos como el tiempo y el uso.
La modelización estadística es un tema de considerable interés y para el que existe un gran cuerpo de conocimiento. En esta sección, proporcionamos solo la información básica que es útil para un administrador de infraestructura, no un investigador o modelador experto. Se pueden consultar otros trabajos, como la variedad de libros recomendados por la Universidad de California, Berkeley, Departamento de Estadística:
sgsa.berkeley.edu/actual-stu... ommended-books
También hay una variedad de programas de software que se pueden utilizar para el modelado estadístico, incluyendo complementos a hojas de cálculo como Microsoft Excel, entornos de modelado general como MATLAB, o programas enfocados en modelización estadística como R, S, Minitab o Statistical Package para el Ciencias Sociales (SPSS). Cualquiera de estos programas de software se puede utilizar para modelar el deterioro de la infraestructura ya que los datos generalmente disponibles para el modelado de deterioro están dentro de las capacidades de cualquiera de estos programas de software. Además, estos programas suelen proporcionar archivos de ayuda y tutoriales que se pueden consultar.
Para los modelos de deterioro, la variable dependiente es típicamente condición expresada como un índice numérico. Las variables explicativas pueden ser el tiempo (como la edad en años desde la última rehabilitación), el uso, la zona meteorológica y otras. Se pueden estimar diferentes modelos de deterioro para diferentes diseños de componentes, como las características del pavimento, o se pueden agregar estas características. Por ejemplo, un modelo de condición lineal simple podría ser:
\[c=\alpha+\beta *(a g e)+\epsilon\]
donde c es un índice de condición (como una escala de 1 a 10), \(\alpha\) y\(\beta\) son coeficientes a estimar y \(\epsilon\) es un término de error modelo. Se ensamblarían una serie de observaciones de c y edad como datos de entrada para su estimación. Entonces, se podría emplear una rutina de software para estimar los valores apropiados de los coeficientes\(\alpha\) y\(\beta\) para el modelo estimado. En estas rutinas, los coeficientes\(\alpha\) y \(\beta\) se calculan para minimizar la suma de desviaciones cuadradas entre la condición y el pronóstico del modelo (representado por los \(\epsilon\) valores).
La ecuación 4.3.1 muestra un modelo de deterioro lineal, lo que significa que la variable explicativa edad se relaciona linealmente con el índice de condición de variable dependiente. Se podrían agregar variables explicativas adicionales al modelo, cada una con un coeficiente a estimar. Además, se pueden utilizar formas de modelo no lineales, como un modelo cuadrático donde la edad entra como variable explicativa tanto lineal como cuadrada:
\ [c=\ alpha+\ beta_ {1} * (a g e) +\ beta_ {2} * (a g e) ^ {2} +\ épsilon\]
Otra forma modelo común es una forma modelo exponencial:
\[c=\alpha *(a g e)^{\beta}\]
Este modelo exponencial a menudo se linealiza para fines de estimación tomando el logaritmo de ambos lados de la ecuación para formar un modelo lineal con respecto a los coeficientes a estimar:
\[\ln (c)=\alpha^{\prime}+\beta *(a g e)+\epsilon\]
Dónde\(\alpha '\) está el logaritmo (en función) de α en la Ecuación 4.3.2. En esta forma lineal, los datos de entrada para estimación serían\(ln(c)\) y edad.
¿Qué modelo de formulario debe elegirse para su uso en cualquier caso particular? En términos generales, las formas simples son preferibles a las formas más complicadas. Además, son preferibles las formas modelo que corresponden a causas razonables de deterioro. Por ejemplo, las formas deseables del modelo de deterioro del pavimento incluirían tanto deterioros a lo largo del tiempo como para diferentes niveles de uso del vehículo.
Como ejemplo, Morous (2011) estimó un modelo polinómico de deterioro de la cubierta del puente en Nebraska basado simplemente en la edad de la cubierta del puente. El modelo estimado fue:
y=10-0.25 * x+0.0093 * x^ {2} -0.0001 * x^ {3}
\[y=10-0.25 * x+0.0093 * x^{2}-0.0001 * x^{3}\]
donde y es calificación de condición (c en la Ec. 4.1-4.4) y x es edad (o edad en la Ec. 4.2.1, 4.3.1-4.3.3). Como se puede observar en la Fig. 4.3.1, el modelo polinómico se acerca a los datos históricos sobre el deterioro del puente. Morous (2011) también reporta el valor R2 de la ecuación de regresión estimada (igual a .99 en la Figura 4.4) que es una medida de 'bondad de ajuste' del modelo a los datos. En este caso, 99% de la variación en la variable dependiente es capturada por el modelo de regresión.
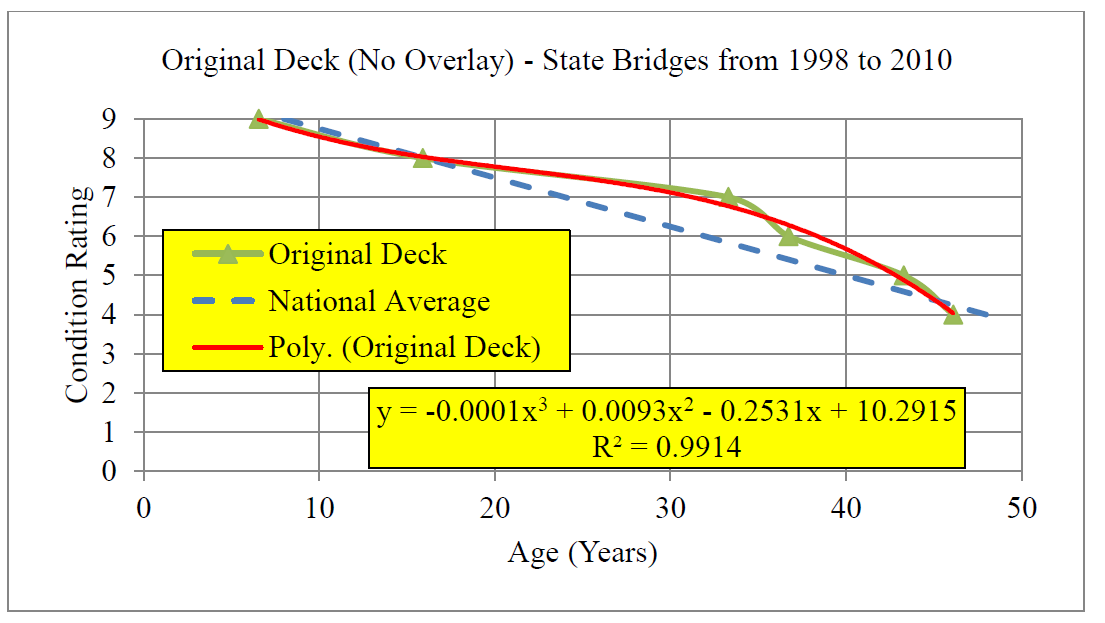
La utilidad de los modelos de regresión de deterioro deriva realmente de situaciones en las que múltiples factores explicativos son de interés, como la edad, el tipo de pavimento y el uso de vehículos (generalmente medidos en cargas equivalentes por eje estándar) para pavimentos de carreteras o cubiertas de puentes. Para el modelo mostrado en la Fig. 4.4, el uso de datos históricos o el modelo de regresión tiene la misma capacidad de pronóstico. Pero con más factores considerados, las representaciones gráficas bidimensionales como la Fig. 4.4 no pueden ser utilizadas directamente.
Los enfoques de regresión suelen hacer suposiciones bastante heroicas sobre los datos disponibles y las formas modelo apropiadas. En particular, generalmente se supone que los valores del término de error ε en las Ecuaciones de las Ecuaciones 4.2.1, 4.3.1 y 4.3.2 se distribuyen normalmente con cero medio, independientes entre sí y con una varianza constante. Es poco probable que algún modelo de deterioro cumpla exactamente con estos supuestos formales. Si nada más, las calificaciones de condición suelen estar restringidas a ser positivas, por lo que no se permiten valores altamente negativos de ε. Además, es poco probable que las observaciones históricas de los componentes sean completamente independientes. Afortunadamente, los modelos de deterioro de regresión suelen ser bastante robustos, por lo que la desviación de los supuestos formales no es un problema práctico para obtener estimaciones razonables de coeficientes. Sin embargo, factores como los términos de error correlacionados hacen problemático el uso de enfoques formales de pruebas estadísticas.
Los pronósticos de los modelos de regresión son inciertos, como es el caso de todos los modelos de deterioro. Con base en historiales pasados y supuestos de distribución, es posible estimar intervalos de confianza para los valores de pronóstico. La Figura 4.3.2 proporciona un ejemplo, con intervalos de confianza para los recibos de impuestos australianos mostrados, donde un intervalo de confianza del 90% sugiere que los recibos pronosticados caerán dentro del intervalo 90% del tiempo. El intervalo de confianza del 90% en este caso para el año siguiente es de 18 a 22.5 como porcentaje del Producto Interno Bruto (PIB) australiano. Desarrollar intervalos formales de confianza sería inusual para la gestión de la infraestructura, pero los propios gerentes siempre deben ser conscientes de que los resultados reales probablemente diferirán de los pronósticos.
.png)
Figura\(\PageIndex{2}\): Forecast for Australia Tax Revenues - Example of Probability Confidence Intervals. Source: By The Commonwealth of Australia. http://www.budget.gov.au/2013-14/con...tachment_b.htm. Creative Commons BY Attribution 3.0 Australia https://creativecommons.org/licenses/by/3.0/au/. Forecast is for Australia tax revenues.


