4.4: Modelos de Deterioro de Markov
- Page ID
- 59647
Los modelos de deterioro de Markov se utilizan en numerosos programas de software de gestión de activos. Los modelos de Markov pueden acomodar fácilmente el uso de índices de condición con valores enteros y estimación de deterioro para períodos de tiempo discretos como un año o una década. Como resultado, los modelos de Markov se pueden combinar con técnicas típicas de evaluación de condiciones y procesos de presupuestación.
Los modelos de Markov son procesos estocásticos con probabilidades de pronóstico de transiciones entre diferentes estados (\(x\), donde \(x\) es un vector de múltiples estados potenciales) en momentos particulares\((t)\) o\(x(t)\). Los modelos de Markov de este tipo a menudo se llaman 'cadenas de Markov' para enfatizar las transiciones entre estados. Para los modelos de componentes de infraestructura, generalmente se asume que los estados son diferentes índices de condición. Si un componente se encuentra en algún estado de condición particular (\(x_i\)) entonces podría permanecer en esa condición o deteriorarse en el próximo año. La Figura 4.4.1 ilustra un proceso con solo tres estados de condición definidos (1 — bueno, 2 — intermedio, 3 — mal estado). Si la condición al inicio del año es el estado 2 (intermedio), entonces el proceso de Markov muestra una probabilidad de 0.8 o 80% de probabilidad de permanecer en la misma condición y una probabilidad 0.2 o 20% de probabilidad de deteriorarse al estado 3. Si el componente comienza en el estado 3 (mal o mal estado), entonces no hay posibilidad de mejora (o un 100% de probabilidad de permanecer en el mismo estado). El Estado 3 es un 'estado absorbente' ya que no hay posibilidad de una transición fuera del estado 3.
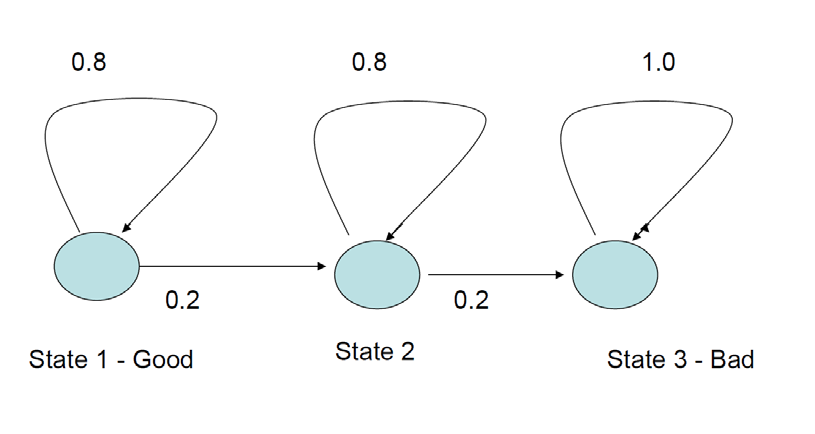
El proceso de Markov en la Figura 4.4.1 ilustra la hipótesis de deterioro puro, en el sentido de que el componente no puede mejorar la condición a lo largo del tiempo. Comenzando en el estado 1, el componente podría deteriorarse al estado 3 dentro de dos años y luego permanecer permanentemente en el estado 3. Más probablemente, el componente permanecería en el estado 1 o el estado 2 por varios años, y el deterioro al estado 3 tomaría varios años. Tenga en cuenta que las probabilidades de transición no cambian con el tiempo, por lo que el modelo de Markov asume que el tiempo que se pasa en cualquier estado no aumenta la probabilidad de deterioro (esto a menudo se llama la 'propiedad sin memoria' de los modelos de Markov).
Un proceso de Markov puede mostrarse en forma gráfica como en la Figura 4.5.1 o como una tabla o matriz de probabilidades de transición. Formalmente, el vector estado es x = (1, 2, 3) y la matriz de transición P tiene tres filas y tres columnas correspondientes a las tres últimas columnas y las tres filas inferiores en la Tabla 4.1.1 (como se muestra en la Figura 4.5.2). Tenga en cuenta que las filas de la matriz de transición deben sumar 1.0 para representar adecuadamente las probabilidades.
| Estado | Para: | 1 | 2 | 3 |
| De: | ||||
| 1 | 0.8 | 0.2 | 0.0 | |
| 2 | 0.0 | 0.8 | 0.2 | |
| 3 | 0.0 | 0.0 | 1.0 | |
¿Qué pasa si el administrador de infraestructura adopta la política de que los componentes en el estado 3 siempre serán rehabilitados al estado 1? En este caso de intervención, habría una transición del estado 3 al estado 1 con una probabilidad de 1.0. Las condiciones de pronóstico (o más precisamente, pronosticar la probabilidad de estados particulares) con un modelo de Markov implica la aplicación de álgebra matricial lineal. En particular, un pronóstico de un período toma las probabilidades de estado existentes en período\(n\)\(\pi_n\), y multiplica la matriz de probabilidad de transición:
\[\pi_{n+1}=\pi_{n} * P\]
El cálculo del pronóstico puede continuar por tantos periodos como quieras. Un pronóstico de periodo\(n\) a periodo\(m\) sería:
\[\\pi_{n+m}=\pi_{n} * P^{m-n} \label{4.3.1}\]
Usando la Eq. \ ref {4.3.1}, un pronóstico de dos periodos a partir de ahora se multiplicarían\(\pi_n\) por\(P*P\). La Figura 4.4.2 ilustra los cálculos para un pronóstico de dos períodos utilizando las probabilidades de transición en la Tabla 4.4.1 y asumiendo que la condición inicial es el estado 1 (buena). Si bien es posible pasar de buen estado a mal estado en dos periodos, la probabilidad de deteriorarse esto rápidamente es de sólo 0.04 o 4%. Lo más probable es que el componente permanezca en buenas condiciones por dos periodos, con probabilidad 0.64 o 64%. Como verificación de los cálculos, tenga en cuenta que las probabilidades de pronóstico suman a uno: \(0.64 + 0.32 + 0.04 = 1.0\).
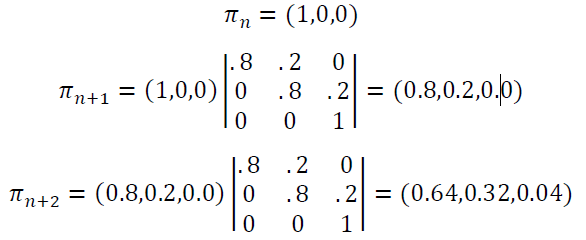.png)
El procedimiento mostrado en la Figura 4.5.2 se puede extender para encontrar la mediana del tiempo hasta la falla del componente. Al continuar pronosticando más hacia el futuro (multiplicando\(\pi\) por P repetidamente), aumentará la probabilidad de ingresar al estado absorbente 3. La mediana del tiempo hasta ingresar a este estado se identifica cuando la probabilidad alcanza 0.5 o 50%. También es posible calcular analíticamente el tiempo esperado o medio antes de la falla del componente. Sin embargo, es probable que la mediana del tiempo se utilice más en la planificación de actividades de mantenimiento y rehabilitación para una gran cantidad de componentes de infraestructura.
Numerosos programas de software pueden ser utilizados para realizar los cálculos de álgebra matricial ilustrados en la Figura 4.5.2. Dos programas populares que tienen funciones de álgebra matricial proporcionadas son el programa de hoja de cálculo EXCEL y el programa de análisis numérico MATLAB.
¿Dónde obtendría un administrador de infraestructura estimaciones de probabilidad de transición como las de la Tabla 4.4.1? El enfoque más común es crear un registro histórico de condiciones y deterioro año a año como se describe en el Capítulo 3: Evaluación de la condición o ilustrado en la Figura 4.1.3. Los registros históricos podrían dar la frecuencia de deterioro para un tipo particular de componente y para una situación particular. También podrían utilizarse juicios periciales, subjetivos, pero estos juicios periciales se basan en el análisis u observación de dicho deterioro a lo largo del tiempo.
Finalmente, hemos presentado en esta sección la forma más simple de modelización de procesos de Markov. Lo hemos hecho porque esta sencilla forma parece ser útil para la gestión de infraestructuras, con muchas aplicaciones de procesos de Markov para componentes como carreteras o puentes. Una variedad de extensiones o variaciones son posibles:
- En lugar de modelar pasos anuales discretos, un modelo de Markov puede usar tiempo continuo. En este caso, las probabilidades de transición se modelan como una distribución de probabilidad exponencial negativa.
- Si la propiedad 'sin memoria' del modelo simple de Markov parece inaceptable, se puede adoptar una suposición Semi-Markov o incluso aumentar el espacio estatal para incluir tanto las condiciones como la edad en los estados condicionales. Desafortunadamente, los modelos resultantes se vuelven más complicados y requieren más datos para una estimación precisa.
Los lectores que deseen una presentación más amplia y matemáticamente rigurosa de los procesos de Markov deben consultar un libro como Grimstead y Snell (2012) que está disponible para su descarga gratuita en internet.


