4.6: Tasas de Fracaso y Probabilidades de Supervivencia

Además de los modelos de deterioro vinculados a los índices de condición de componentes, los modelos de deterioro también pueden expresarse como probabilidades de falla (o supervivencia como la inversa de falla) en diferentes momentos del tiempo. Por supuesto, la dificultad para utilizar este enfoque para los componentes de infraestructura es definir lo que constituye 'fracaso'. Para un dispositivo mecánico como un elevador, la falla podría considerarse simplemente como dejar de funcionar. Para el pavimento de una calzada, se podría considerar que el pavimento ha fallado cuando no se brinda un nivel de servicio deseado, aunque la calzada aún pueda ser transitable a baja velocidad.

Las tasas de falla se definen como la probabilidad de falla en el siguiente intervalo de tiempo asumiendo que el componente no ha fallado hasta el momento presente. La tasa de fallas generalmente es mayor que la función de densidad de fallas ya que el componente ha sobrevivido durante uno o más períodos. Dado que los administradores de infraestructura están preocupados por pronosticar la posibilidad de falla en el siguiente período o dos para la toma de decisiones, la tasa de fallas generalmente es de mayor interés en lugar de la probabilidad directa de falla de un componente en un momento dado en el futuro. Utilizaremos un ejemplo numérico para ilustrar las tasas de fracaso, la probabilidad de supervivencia y las probabilidades de falla utilizando los datos que se muestran en la Tabla 4.6.1.

Cuadro 4.6.1: Ilustración numérica de las probabilidades de fracaso y supervivencia y tasas de fracaso

Periodo (Año)	Probabilidad de Fracaso en Periodo\(f(t)\)	Probabilidad acumulada de falla\(F(t)\)	Probabilidad acumulada de supervivencia\(R(t)\)	Tasa de Fallas en Periodo\(\lambda(t)\)
1	0.10	0.10	0.90	0.100
2	0.02	0.12	0.88	0.022
3	0.02	0.14	0.86	0.023
4	0.02	0.16	0.84	0.023
5	0.02	0.18	0.82	0.024
6	0.02	0.20	0.80	0.024
7	0.10	0.30	0.70	0.125
8	0.20	0.50	0.50	0.286
9	0.20	0.70	0.30	0.400
10	0.30	1.0	0.00	1.000

Probabilidad Acumulada de Fallo\(F(t)\) es\(F(t-1) + f(t)\). Probabilidad Acumulada de Supervivencia R es\(1 - F(t)\). \(\lambda(t)\)La tasa de fallas es\(\frac{f(t)}{R(t)}\) o\ (R (t) - \ frac {R (t-1)} {R (t)}\).

El Cuadro 4.6.1 ilustra un componente que se encuentra en buen estado en la actualidad pero que se espera que, ciertamente, falle después de diez años de uso. La probabilidad de falla f (t) (Columna 2) representa una estimación de falla en cada periodo, con un 10% de falla inmediatamente (durante un periodo de allanamiento), un periodo de baja probabilidad de falla en los años 2-6 (uso regular) y luego una probabilidad creciente de falla en los años 8 a 10 (desgastado). La probabilidad acumulada de falla\(F(t)\) es la suma de probabilidades de falla para periodo\(t\) y periodos anteriores. Comienza en cero y aumenta de manera constante a 1.0 (cierta falla) en el año 10. La probabilidad acumulada de supervivencia\(R(t)\) es la inversa de la probabilidad acumulativa de falla,\(1 – F(t)\). La tasa de fallas se\(\lambda(t)\) puede calcular como:

\[\lambda(t)=\frac{f(t)}{R(t)}=R(t)-\frac{R(t-1)}{R(t)}\]

Tiene un valor de 0.1 en el periodo 1, reflejando la posibilidad de falla durante el periodo de allanamiento. Después de esto, la tasa de fallas es relativamente baja pero aumenta lentamente. Durante el desgaste final de nuestro periodo, la tasa de fallas aumenta sustancialmente. Obsérvese que la suma de las tasas de fallas durante todos los periodos es superior a 1, por lo que la tasa de fallas no es una probabilidad. No obstante, para la toma de decisiones, a un administrador de infraestructura le resultaría útil saber en el año 5 que el riesgo de falla en el próximo periodo es pequeño (0.024). No obstante, en el año 8, si bien el componente aún puede estar funcionando, el riesgo de falla en el siguiente periodo es sustancial (0.400). El patrón de las probabilidades y tasas de falla en el Cuadro 4.4.1 es común para los componentes de infraestructura y a menudo se denomina “forma de bañera” como se ilustra en la Figura 4.6.1 a continuación.

Figura\(\PageIndex{1}\): Ilustración de una Curva de Bañera. Fuente: Por Bathtub_curve.jpg: Obra derivada de Wyatts: McSush (Bathtub_curve.jpg) [Dominio público], vía Wikimedia Commons. https://commons.wikimedia.org/wiki/F...htub_curve.svg.

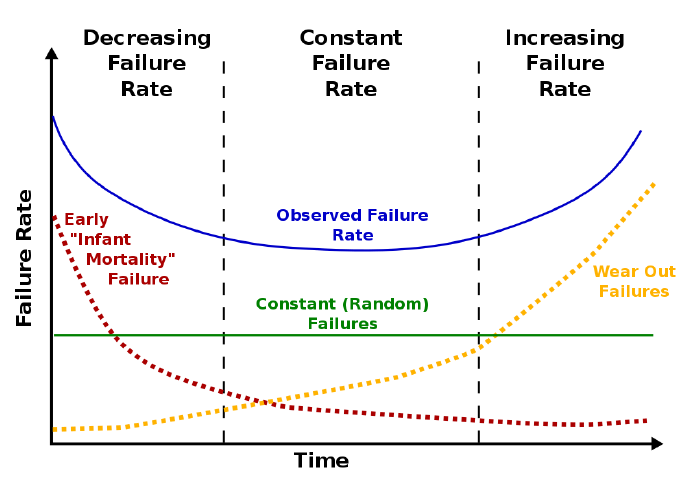
La rotura inicial en el uso de un componente a menudo revela fallas de diseño o fabricación que pueden causar fallas. Después de este periodo de allanamiento, se produce un periodo (ojalá largo) de uso regular y bajo riesgo de falla. A medida que el componente se desgasta, aumenta el riesgo de falla. Las figuras 4.6.2 y 4.6.3 ilustran adicionalmente estos periodos gráficamente para la probabilidad de falla y las probabilidades acumuladas.

Figura\(\PageIndex{2}\): Probabilidad de falla de componentes en el año t a partir de la Tabla 4.4.1 Datos

Figura\(\PageIndex{3}\): Probabilidades acumuladas de falla y supervivencia a partir de la Tabla 4.4.1 Datos

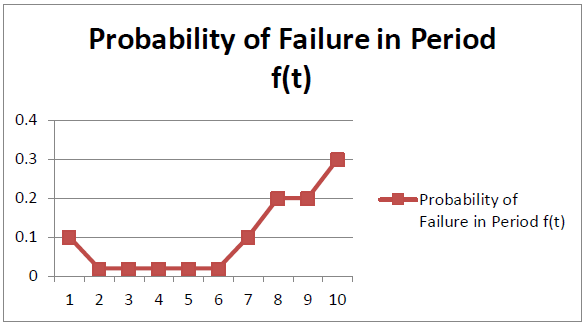
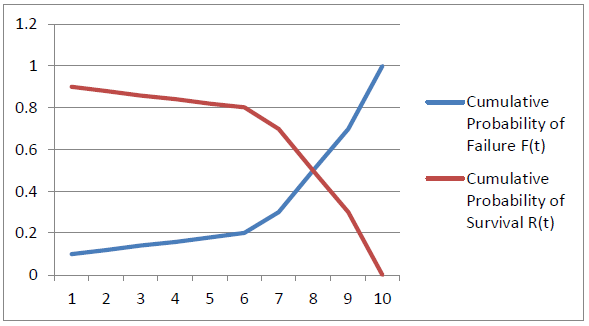
El ejemplo numérico presentado anteriormente no asumió ninguna forma distribucional particular para las probabilidades de falla. Sin embargo, muchas aplicaciones de modelos de fallas asumen alguna distribución particular y utilizan datos históricos para estimar los parámetros de la distribución. Discutiremos dos distribuciones utilizadas de esta manera: la exponencial y la de Weibull.

La forma del modelo de falla exponencial para la probabilidad acumulativa de falla es:

\ [F (t) =\ int_ {0} ^ {t}\ alfa * e^ {-\ alfa t} d t=1-e^ {-\ alfa t}\]

Que es la integral de 0 a tiempo\(t\) del parámetro α veces exponencial de\(-\alpha * t\) o, más simplemente, uno menos el exponencial de\(-\alpha * t\). La función de densidad de probabilidad de falla para las distribuciones exponenciales es\ (\ alpha * e^ {-\ alpha t}\). La función exponencial tiene solo un parámetro (\(\alpha\) en esta notación) y el tiempo promedio hasta el fallo es el recíproco de este parámetro (\(\frac{1}{\alpha}\)). La tasa de fallas es constante en el tiempo con un valor del parámetro α (calculado a partir de la Ec. 4.6.2 como\ (\ alpha*\ frac {e^ {-\ alpha t}} {e^ {-\ alpha t}} = \ alpha\). Con el signo negativo en las distribuciones de falla acumulativa y de densidad, la función exponencial a menudo se conoce como una 'distribución exponencial negativa'.

Las figuras 4.6.4 y 4.6.5 ilustran la forma de la función exponencial para diferentes valores de parámetros. La probabilidad de falla acumulativa aumenta inicialmente de manera relativamente rápida (a excepción de los valores bajos del parámetro,\(\alpha\) continúa aumentando lentamente durante un largo período de tiempo.

Figura\(\PageIndex{4}\): Probabilidades de falla acumuladas para modelos de falla exponencial. Fuente: Por Skbkekas - Obra propia, CC BY 3.0, https://commons.wikimedia.org/w/inde...? curid=9508326 vía Wikipedia Commons, https://en.Wikipedia.org/wiki/Expone...l_distribution). Este gráfico utiliza\(\lambda\) para el parámetro de distribución en lugar de\(\alpha\),\(x\) para el período de tiempo en lugar de\(t\) y\(P(X \leq x)\) para\(F(t)\).

Figura\(\PageIndex{5}\): Probabilidades de densidad para modelos de falla exponencial. Fuente: Por Skbkekas - Obra propia, CC BY 3.0, https://commons.wikimedia.org/w/inde...? curid=9508311 vía Wikipedia Commons. Este gráfico utiliza\(\lambda\) para el parámetro de distribución en lugar de\(\alpha\),\(x\) para el período de tiempo en lugar de\(t\) y\(P(x)\) para\(F(t)\).

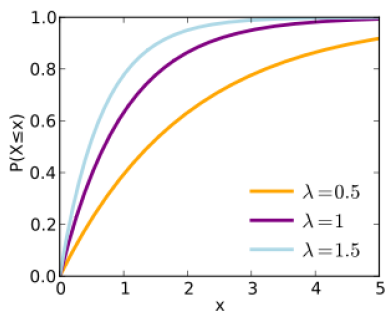
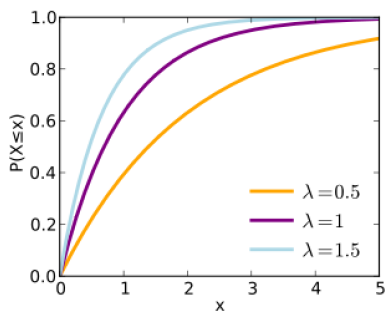
La estimación del parámetro\(\alpha\) es relativamente simple en la práctica. Dado un conjunto de observaciones de fallas de componentes, el parámetro α es el inverso del tiempo promedio hasta el fallo observado en la muestra.

Una segunda distribución que a menudo se asume para los modelos de falla es la distribución de Weibull o 'eventos extremos'. El término “eventos extremos” refleja el uso de la distribución de Weibull para modelar eventos como la probabilidad de terremotos o velocidades del viento huracanado. También refleja la noción de que la distribución devuelve la probabilidad del valor más extremo obtenido de una serie de resultados de variables aleatorias. Para los componentes de infraestructura que involucran un gran número de piezas que podrían fallar, esta analogía es apropiada. La distribución lleva el nombre de Wallodi Weibull, un ingeniero y matemático sueco que vivió en el siglo XX.
La forma general de la distribución de Weibull incluye tres parámetros. Usando la notación de NIST (2016), los parámetros son \(\mu\) (llamado parámetro location),\(\gamma\) (llamado parámetro shape) y\(\alpha\) (llamado parámetro scale). La función de densidad de probabilidad de falla se muestra a continuación,\(x\) representando el tiempo:

\ [f (x) =\ frac {\ lambda} {\ alfa}\ izquierda (\ frac {x-\ mu} {\ alfa}\ derecha) ^ {(\ lambda-1)} e^ {\ izquierda (-\ izquierda (\ frac {x-\ mu} {\ alfa}\ derecha) ^ {\ lambda}\ derecha)}\ text {donde} x\ geq\ mu;\ lambda,\ alfa>0\]

Se pueden obtener formas más simples de la función de distribución de Weibull asumiendo valores del parámetro de ubicación (como \(\mu = 0\)) y el parámetro de escala (como\(alpha = 1\)). Así, se pueden obtener una, dos o tres formas de parámetros.

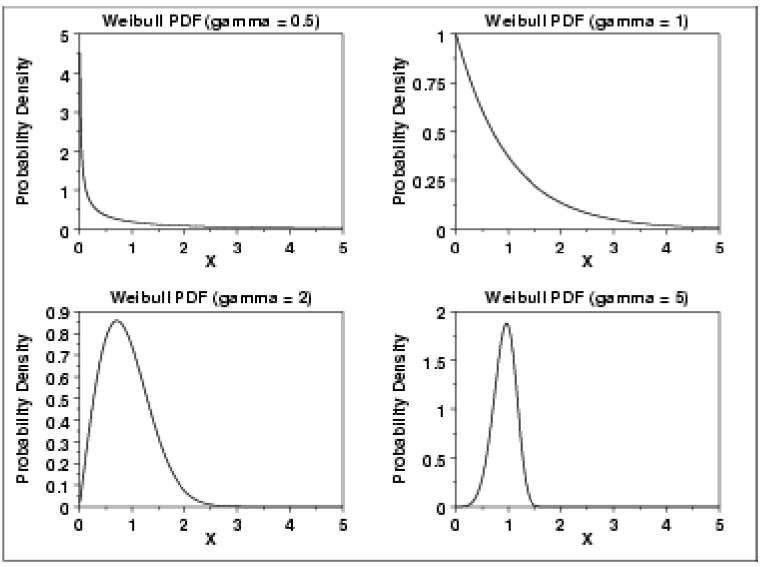
Con diferentes valores de los tres parámetros, se puede obtener una amplia variedad de formas de distribución. La Figura 4.6.6 ilustra los efectos de diferentes valores de solo el parámetro shape.

Figura\(\PageIndex{6}\): Funciones de Densidad de Probabilidad de Fallo para la Distribución Weibull. Fuente: NIST 2016, Dominio Público. Funciones de densidad de probabilidad para la distribución de Weibull con diferentes valores del parámetro shape (\(\gamma\)o gamma en la figura) y el factor de ubicación (\(\mu\)) cero y el factor de escala (\(\alpha\)) uno.